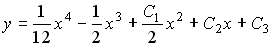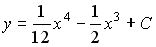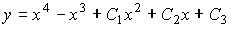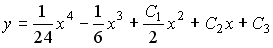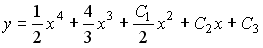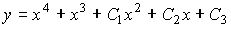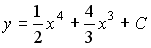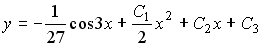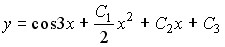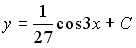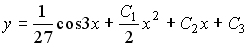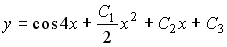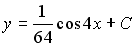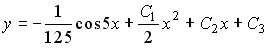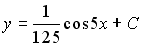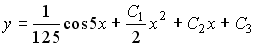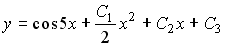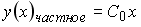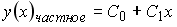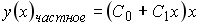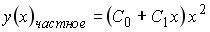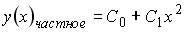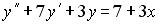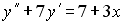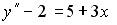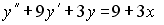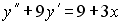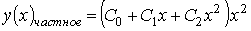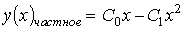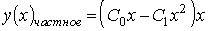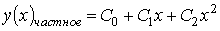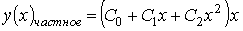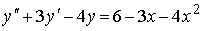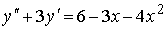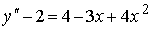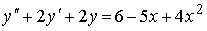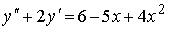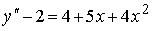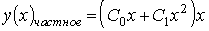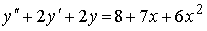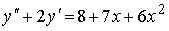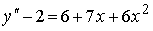Установите соответствие между дифференциальным уравнением и его видом

4) линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами

Задание #118

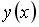
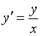
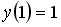
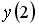
Если — решение уравнения , удовлетворяющее условию , тогда равно …

__________2_________________

Задание #119

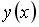
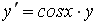
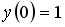
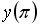
Если — решение уравнения , удовлетворяющее условию , тогда равно …

________1___________________

Задание #120

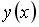
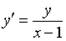
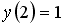
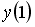
Если — решение уравнения , удовлетворяющее условию , тогда равно …

_________0__________________

Задание #121

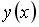
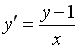
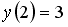
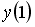
Если — решение уравнения , удовлетворяющее условию , тогда равно …

___________2________________

Задание #122

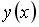
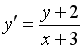
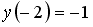
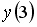
Если — решение уравнения , удовлетворяющее условию , тогда равно …

___________4________________

Задание #123

Общее решение дифференциального уравнения 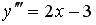имеет вид …

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание #124

Общее решение дифференциального уравнения 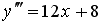имеет вид …

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание #125

Общее решение дифференциального уравнения 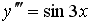имеет вид …

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание #126

Общее решение дифференциального уравнения 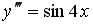имеет вид …

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание #127

Общее решение дифференциального уравнения имеет вид …

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание #128

Установите соответствие между дифференциальным уравнением и общим видом его частного решения

Укажите соответствие для всех 3 вариантов ответа:

1)

2)

3)

4)

5)

_2_

_3_

_4_

Задание #129

Установите соответствие между дифференциальным уравнением и общим видом его частного решения

Укажите соответствие для всех 3 вариантов ответа:

1)

2)

3)

4)

5)

_3_

_2_

_4_

Задание #130

Установите соответствие между дифференциальным уравнением и общим видом его частного решения …

Укажите соответствие для всех 3 вариантов ответа:

1)

2)

3)

4)

5)

_4_

_5_

_1_

Задание #131

Установите соответствие между дифференциальным уравнением и общим видом его частного решения …

Укажите соответствие для всех 3 вариантов ответа:

1)

2)

3)

4)

5)

_2_

_1_

_5_

Задание #132

Установите соответствие между дифференциальным уравнением и общим видом его частного решения …

Укажите соответствие для всех 3 вариантов ответа:

1)

2)

3)

4)

5)

_3_

_4_

_5_

Задание #133

Бросают 2 монеты. События А — «цифра на первой монете» и В — «герб на второй монете» являются:

Выберите один из 4 вариантов ответа:

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Установите соответствие между дифференциальным уравнением и его видом

Дифференциальное уравнение y´+3xy=
является __________(каким?) дифференциальным уравнением первого порядка (вставить слово)
Общее решение линейного дифференциального уравнения
y´´+4y=0 имеет вид
Система дифференциальных уравнений

эквивалентна уравнению вида
Система дифференциальных уравнений

эквивалентна уравнению вида
В связи с дифференциальными уравнениями рассматривают ___ решения
В связи с дифференциальными уравнениями рассматривают ____ решения
График любого решения дифференциального уравнения называют______ (завершите определение словосочетанием)
Дано линейное однородное дифференциальное уравнение y´´–4y´+4y=0 Его общим решением является функция
Дано линейное однородное дифференциальное уравнение y´´–6y´+5y=0, тогда его общее решение имеет вид
Даны уравнения и . Укажите верные для них утверждения
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение x2y´=x2+y2 является уравнением
Дифференциальное уравнение x3y´+x2y+2=0 является
Дифференциальное уравнение y´+xy=x3y2 является уравнением ___________ (укажите название)
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид:
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения = 0 характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Завершите условие Уравнение вида будет однородным в том и только том случае, когда и являются однородными функциями _________ ( слово) порядка
Интегральная кривая дифференциального уравнения – это
Корни характеристическое уравнение есть
Нахождение функции , определенной на некотором интервале , имеющей на производную , такую, что для всех и удовлетворяющей условию , где и в точке определена функция , называется задачей
Общее решение дифференциального уравнения в областибудет функция
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения xy´´=y´ имеет вид
Общее решение линейного неоднородного дифференциального уравнения имеет вид
Общее решение линейного однородного дифференциального уравнения y´´–16y=0 имеет вид
Общее решение уравнения y´=e–2x имеет вид
Общее решение уравнения y´´+y=x+2 имеет вид
Общее решение уравнения y´´–y´=ex имеет вид
Общий интеграл дифференциального уравнения имеет вид
Общим решением линейного дифференциального уравнения y´´+9y=0 является функция
Общим решением системы дифференциальных уравнений , является
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Порядок дифференциального уравнения – это неизвестной функции
При нахождении общего решения неоднородной системы линейных дифференциальных уравнений -го порядка используют
При решении линейных дифференциальных уравнений с постоянными коэффициентами используют
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Решение дифференциального уравнения второго порядка можно свести к решению дифференциального уравнения первого порядка в двух случаях Выберите их
Решить дифференциальное уравнение – это значит найти
Семейству линий сопоставьте огибающую
Семейству линий сопоставьте огибающую
Семейству линий сопоставьте огибающую
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполняется в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполняется в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Укажите верные для уравнений Клеро и Лагранжа утверждения
Укажите соответствие между типом дифференциального уравнения второго порядка и методом его решения
Укажите соответствия между дифференциальными уравнениями и их характеристическими уравнениями
Укажите соответствия между дифференциальными уравнениями и их частными решениями
Укажите соответствия между дифференциальными уравнениями и корнями их характеристических уравнений
Укажите соответствия между функциями и дифференциальными уравнениями
Укажите соответствия между функциями и дифференциальными уравнениями
Укажите утверждения верные для дифференциального уравнения Лагранжа
Укажите утверждения, верные для дифференциального уравнения Клеро
Установить зависимость вида общего решения дифференциального уравнения от корней соответствующего характеристического уравнения
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальными уравнениями первого порядка и их названием
Установить соответствие между линейным однородным дифференциальным уравнением и видом его общего решения
Установить соответствие между линейным однородным дифференциальным уравнением и видом общего решения этого уравнения
Установить соответствие между линейным однородным дифференциальным уравнением и его характеристическим многочленом
Установить соответствие между линейными однородными дифференциальными уравнением и его общим решением
Установить соответствие между характеристическим многочленом и линейным однородным дифференциальным уравнением
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Частное решение дифференциального уравнения есть
Частное решение дифференциального уравнения есть
Частное решение дифференциального уравнения есть
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение линейного неоднородного дифференциального уравнения второго порядка y´´+4y=ex имеет вид
Частное решение уравнения при есть
Частное решение уравнения при есть

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Виды дифференциальных уравнений

Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.

В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.

Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.

Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.

Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».

Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1 -го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2 -го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.

Напомним, что y ‘ = d x d y , если y является функцией аргумента x .

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )

Начнем с примеров таких уравнений.

y ‘ = 0 , y ‘ = x + e x — 1 , y ‘ = 2 x x 2 — 7 3

Оптимальным для решения дифференциальных уравнений f ( x ) · y ‘ = g ( x ) является метод деления обеих частей на f ( x ) . Решение относительно производной позволяет нам прийти к уравнению вида y ‘ = g ( x ) f ( x ) . Оно является эквивалентом исходного уравнения при f ( x ) ≠ 0 .

Приведем примеры подобных дифференциальных уравнений:

e x · y ‘ = 2 x + 1 , ( x + 2 ) · y ‘ = 1

Мы можем получить ряд дополнительных решений в тех случаях, когда существуют значения аргумента х , при которых функции f ( x ) и g ( x ) одновременно обращаются в 0 . В качестве дополнительного решения в уравнениях f ( x ) · y ‘ = g ( x ) при заданных значениях аргумента может выступать любая функция, определенная для заданного значения х .

Наличие дополнительных решений возможно для дифференциальных уравнений x · y ‘ = sin x , ( x 2 — x ) · y ‘ = ln ( 2 x 2 — 1 )

Ознакомиться с теоретической частью и примерами решения задач таких уравнений вы можете в разделе «Простейшие дифференциальные уравнения 1 -го порядка».

Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )

Поговорим теперь об уравнениях с разделенными переменными, которые имеют вид f ( y ) d y = g ( x ) d x . Как следует из названия, к данному виду дифференциальных уравнений относятся выражения, которые содержат переменные х и у , разделенные знаком равенства. Переменные находятся в разных частях уравнения, по обе стороны от знака равенства.

Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x

К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:

y 2 3 d y = sin x d x , e y d y = ( x + sin 2 x ) d x

Для того, чтобы прийти от ДУ с разделяющимися переменными к ДУ с разделенными переменными, необходимо разделить обе части уравнения на произведение f 2 ( y ) ⋅ g 1 ( x ) . Так мы придем к уравнению f 1 ( y ) f 2 ( y ) d y = g 2 ( x ) g 1 ( x ) d x . Преобразование можно будет считать эквивалентным в том случае, если одновременно f 2 ( y ) ≠ 0 и g 1 ( x ) ≠ 0 . Если хоть одно из условий не будет соблюдаться, мы можем потерять часть решений.

В качестве примеров дифференциальных уравнений с разделяющимися переменными можно привести следующие из них: d y d x = y · ( x 2 + e x ) , ( y 2 + a r c cos y ) · sin x · y ‘ = cos x y .

К уравнениям с разделяющимися переменными мы можем прийти от ряда дифференциальных уравнений других видов путем замены переменных. Например, мы можем подставить в исходное уравнение z = a x + b y . Это позволит нам перейти к дифференциальному уравнению с разделяющимися переменными от дифференциального уравнения вида y ‘ = f ( a x + b y ) , a , b ∈ R .

Подставив z = 2 x + 3 y в уравнение y ‘ = 1 e 2 x + 3 y получаем d z d x = 3 + 2 e z e z .

Заменив z = x y или z = y x в выражениях y ‘ = f x y или y ‘ = f y x , мы переходим к уравнениям с разделяющимися переменными.

Если произвести замену z = y x в исходном уравнении y ‘ = y x · ln y x + 1 , получаем x · d z d x = z · ln z .

В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.

Предположим, что в условии задачи нам дано уравнение y ‘ = y 2 — x 2 2 x y . Нам необходимо привести его к виду y ‘ = f x y или y ‘ = f y x . Для этого нам нужно разделить числитель и знаменатель правой части исходного выражения на x 2 или y 2 .

Нам дано уравнение y ‘ = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 , a 1 , b 1 , c 1 , a 2 , b 2 , c 2 ∈ R .

Для того, чтобы привести исходное уравнение к виду y ‘ = f x y или y ‘ = f y x , нам необходимо ввести новые переменные u = x — x 1 v = y — y 1 , где ( x 1 ; y 1 ) является решением системы уравнений a 1 x + b 1 y + c 1 = 0 a 2 x + b 2 y + c 2 = 0

Введение новых переменных u = x — 1 v = y — 2 в исходное уравнение y ‘ = 5 x — y — 3 3 x + 2 y — 7 позволяет нам получить уравнение вида d v d u = 5 u — v 3 u + 2 v .

Теперь выполним деление числителя и знаменателя правой части уравнения на u . Также примем, что z = u v . Получаем дифференциальное уравнение с разделяющимися переменными u · d z d u = 5 — 4 z — 2 z 2 3 + 2 z .

Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».

Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )

Приведем примеры таких уравнений.

К числу линейных неоднородных дифференциальных уравнений 1 -го порядка относятся:

y ‘ — 2 x y 1 + x 2 = 1 + x 2 ; y ‘ — x y = — ( 1 + x ) e — x

Для решения уравнений этого вида применяется метод вариации произвольной постоянной. Также мы можем представить искомую функцию у в виде произведения y ( x ) = u ( x ) v ( x ) . Алгоритмы применения обоих методов мы привели в разделе «Линейные неоднородные дифференциальные уравнения первого порядка».

Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a

Приведем примеры подобных уравнений.

К числу дифференциальных уравнений Бернулли можно отнести:

y ‘ + x y = ( 1 + x ) e — x y 2 3 ; y ‘ + y x 2 + 1 = a r c t g x x 2 + 1 · y 2

Для решения уравнений этого вида можно применить метод подстановки z = y 1 — a , которая выполняется для того, чтобы свести исходное уравнение к линейному дифференциальному уравнению 1 -го порядка. Также применим метод представления функции у в качестве y ( x ) = u ( x ) v ( x ) .

Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.

Уравнения в полных дифференциалах P ( x , y ) d x + Q ( x , y ) d y = 0

Если для любых значений x и y выполняется ∂ P ( x , y ) ∂ y = ∂ Q ( x , y ) ∂ x , то этого условия необходимо и достаточно, чтобы выражение P ( x , y ) d x + Q ( x , y ) d y представляло собой полный дифференциал некоторой функции U ( x , y ) = 0 , то есть, d U ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y . Таким образом, задача сводится к восстановлению функции U ( x , y ) = 0 по ее полному дифференциалу.

Выражение, расположенное в левой части записи уравнения ( x 2 — y 2 ) d x — 2 x y d y = 0 представляет собой полный дифференциал функции x 3 3 — x y 2 + C = 0

Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».

Видео:Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать

Дифференциальные уравнения второго порядка

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = 0 , p , q ∈ R

Линейное однородное дифференциальное уравнение с постоянными коэффициентами обычно решается достаточно просто. Нам необходимо найти корни характеристического уравнения k 2 + p k + q = 0 . Здесь возможны три варианта в зависимости от различных p и q :

• действительные и различающиеся корни характеристического уравнения k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
• действительные и совпадающие k 1 = k 2 = k , k ∈ R ;
• комплексно сопряженные k 1 = α + i · β , k 2 = α — i · β .

Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:

• y = C 1 e k 1 x + C 2 e k 2 x ;
• y = C 1 e k x + C 2 x e k x ;
• y = e a · x · ( C 1 cos β x + C 2 sin β x ) .

Пример 13

Предположим, что у нас есть линейное однородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами y ‘ ‘ + 3 y ‘ = 0 . Найдем корни характеристического уравнения k 2 + 3 k = 0 . Это действительные и различные k 1 = — 3 и k 2 = 0 . Это значит, что общее решение исходного уравнения будет иметь вид:

y = C 1 e k 1 x + C 2 e k 2 x ⇔ y = C 1 e — 3 x + C 2 e 0 x ⇔ y = C 1 e — 3 x + C 2

Восполнить пробелы в теоретической части и посмотреть подробный разбор примеров по теме можно в статье «Линейные однородные дифференциальные уравнения 2 -го порядка с постоянными коэффициентами».

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = f ( x ) , p , q ∈ R

Основным способом решение уравнений данного вида является нахождение суммы общего решения y 0 , которое соответствует линейному однородному дифференциальному уравнению y ‘ ‘ + p y ‘ + q y = 0 , и частного решения y

исходного уравнения. Получаем: y = y 0 + y

Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y

мы можем методом неопределенных коэффициентов при определенном виде функции f ( x ) , которая расположена в правой части записи исходного выражения. Также применим метод вариации произвольных постоянных.

К числу линейных неоднородных дифференциальных уравнений 2 -го порядка с постоянными коэффициентами относятся:

y ‘ ‘ — 2 y ‘ = ( x 2 + 1 ) e x ; y ‘ ‘ + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x

Теоретические выкладки и подробный разбор примеров по теме можно найти в разделе «ЛНДУ 2 -го порядка с постоянными коэффициентами».

Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )

Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.

На некотором отрезке [ a ; b ] общее решение линейного однородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 представлено линейной комбинацией двух линейно независимых частных решений y 1 и y 2 этого уравнения, то есть, y = C 1 y 1 + C 2 y 2 .

Частные решения мы можем выбрать из систем независимых функций:

1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 x , e k 2 x , . . . , e k n x 3 ) e k 1 x , x · e k 1 x , . . . , x n 1 · e k 1 x , e k 2 x , x · e k 2 x , . . . , x n 2 · e k 2 x , . . . e k p x , x · e k p x , . . . , x n p · e k p x 4 ) 1 , c h x , s h x

Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.

Возьмем для примера линейное однородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = 0 .

Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ, а y

частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y

нам поможет метод вариации произвольных постоянных.

Возьмем для примера линейное неоднородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = x 2 + 1 .

Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».

Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Дифференциальные уравнения высших порядков

Дифференциальные уравнения, допускающие понижение порядка

Мы можем провести замену y ( k ) = p ( x ) для того, чтобы понизить порядок исходного дифференциального уравнения F ( x , y ( k ) , y ( k + 1 ) , . . . , y ( n ) ) = 0 , которое не содержит искомой функции и ее производных до k — 1 порядка.

В этом случае y ( k + 1 ) = p ‘ ( x ) , y ( k + 2 ) = p ‘ ‘ ( x ) , . . . , y ( n ) = p ( n — k ) ( x ) , и исходное дифференциальное уравнение сведется к F 1 ( x , p , p ‘ , . . . , p ( n — k ) ) = 0 . После нахождения его решения p ( x ) останется вернуться к замене y ( k ) = p ( x ) и определить неизвестную функцию y .

Дифференциальное уравнение y ‘ ‘ ‘ x ln ( x ) = y ‘ ‘ после замены y ‘ ‘ = p ( x ) станет уравнением с разделяющимися переменными y ‘ ‘ = p ( x ) , и его порядок с третьего понизится до первого.

В уравнении, которое не содержит аргумента х и имеет вид F ( y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 , порядок может быть заменен на единицу следующим образом: необходимо провести замену d y d x = p ( y ) , где p ( y ( x ) ) будет сложной функцией. Применив правило дифференцирования, получаем:

d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.

Рассмотрим решение уравнения 4 y 3 y ‘ ‘ = y 4 — 1 . Путем замены d y d x = p ( y ) приведем исходное выражение к уравнению с разделяющимися переменными 4 y 3 p d p d y = y 4 — 1 .

Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».

Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x )

Решение уравнений данного вида предполагает выполнение следующих простых шагов:

• находим корни характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 ;
• записываем общее решение ЛОДУ y 0 в стандартной форме, а общее решение ЛНДУ представляем суммой y = y 0 + y

— частное решение неоднородного дифференциального уравнения.

Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y

целесообразно использовать метод вариации произвольных постоянных.

Линейному неоднородному ДУ с постоянными коэффициентами y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = x cos x + sin x соответствует линейное однородное ДУ y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = 0 .

Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».

Линейные однородные и неоднородные дифференциальные уравнения высших порядков y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 и y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )

Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ, а y

— частное решение неоднородного дифференциального уравнения.

y 0 представляет собой линейную комбинацию линейно независимых функций y 1 , y 2 , . . . , y n , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 в тождество. Частные решения y 1 , y 2 , . . . , y n обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.

После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y

Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».

Видео:Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2

Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.

📺 Видео

Решение однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Определяем тип ДУ 1Скачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

Видеоурок "Нахождение частных решений по виду правой части"Скачать

#Дифуры I. Урок 9. Уравнение РиккатиСкачать

Дифференциальные уравнения. 11 класс.Скачать

Дифференциальные уравнения с разделяющими переменными. 11 класс.Скачать

Дифференциальные уравнения для самых маленькихСкачать

Основные понятия дифференциальных уравнений от bezbotvyСкачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Лекция 10 по курсу "Дифференциальные уравнения"Скачать