Установите какие из следующих записей являются уравнениями с одной переменной х 3 5 12х

Практическое занятие 2.1. Выражения, уравнения, неравенства.

Задания для самостоятельной работы

1. Среди следующих записей укажите числовые выражения:

а) 42:5; б) 27; в) 32+ -):14; г) 2·7 = 7·2;

д) (17+ 13):10-15; е) 142 > 71·2; ж) 37 – 48+3х

1. Какие из следующих выражений имеют смысл, если рассматри­вать их на множестве натуральных чисел:

а) (135+67)· 12; б) (135 — 217):2; в) 362:4?

1. Какие из нижеприведенных записей являются выражениями с переменными:

а) 8+0,3b; б) 21 — (4 + у); в) х + 2у

а) ; б) действительных чисел.

1. Какие из следующих равенств являются тождествами на множе­стве действительных чисел:

а) 3р + 5m = 5m + 3р; в) 3р · 5m = 5m · 3р;

б) 3р – 5m = 5m — 3р; г) 3р:5m = 5m:3р?

1. Обоснуйте каждый шаг в преобразованиях следующих выражений:

а) 324·5 = (300+20+4) · 5 = 300· 5+20·5+4·5 = 500+100+20 = 1500+ 120 = 1620;

б) 97·12 = (100 — 3) · 12 = 100 ·12 — 3·12 = 1200 — 36 = 1100+(100 — 36) =1164;

в) 5(1-2х)+10х = 5 — 10х+10х = 5.

1. Упростите выражение путем тождественных преобразований:

а) 6(2аb — 3) + 2а (6b — 5); б) (12а — 16b):4 — (10а — 4b).

1. Сравните значения выражений, не выполняя действий:

а) (30 + 56) ·5 и 30·5 + 56·5;

б)(19 + 4) ·7 и 19·7 + 10·7;

в) (14 — 7) ·6 и 16·6 — 7·6;

г) (18 — 9) ·7 и 18·7 — 11·7.

1. Решите задачу; решение запишите в виде выражения:

На туристическую базу прибыли в один день 150 туристов, на другой день 170. Чтобы пойти по маршрутам, 200 туристов разби­лись на группы, по 20 человек в каждой, а остальные по 15 человек в группе. Сколько получилось групп?

1. Среди следующих записей найдите числовые равенства и неравенства:

а) 3х + 4=57:3; б) 34 — 48:12=(7 + 8) ·9; в) 39·3 + 74 — 53; г) 37 344 + 148:74

1. Проверьте, истинны ли числовые равенства:

13 · 93 = 31·39, 14·82 = 41·28, 23·64 = 32·46.

Можно ли утверждать, что произведение лю­бых двух натуральных чисел не изменится, если в каждом множителе переставить цифры?

1. Известно, что х > у — истинное неравенство. Будут ли истинными следующие неравенства:

а) 2х > 2у; в) 2х — 7 » или « 2 — 2х + 5 = 0.

1. Уравнение 2х 4 + 4х 2 — 6 = 0 задано на множестве натуральных чисел. Объясните, почему число 1 является корнем этого уравнения, а 2 и -1 не являются его корнями.
2. В уравнении (х + . )(2х + 5) — (х — 3)(2х + 1) = 20 одно число стерто и заменено точками. Найдите стертое число, если известно, что корнем этого уравнения является число 2.
3. Сформулируйте условия, при которых:

а) число 5 является корнем уравнения f(х)= g (х);

б) число 7 не является корнем уравнения f(х)= g (х).

1. Установите, какие из следующих пар уравнений равносильны на множестве действительных чисел:

а) 3 + 7х = — 4 и 2(3 + 7х) = -8;

б) 3 + 7х = — 4 и 6 + 7x = -1;

в) 3 + 7х = — 4 и х + 2 = 0.

1. Решите уравнения (все они заданы на множестве действительных чисел) и обоснуйте все преобразования, выполняемые в процессе их упрощения:

а) ; б)

в) (2 — х)2 — х(х + 1,5) = 4.

1. Учащийся решил уравнение 5х + 15 = 3х + 9 следующим обра­зом: вынес за скобки в левой части число 5, а в правой число 3, полу­чил уравнение 5(х + 3) = 3(х + 3), а затем разделил обе части на вы­ражение х + 3. Получил равенство 5 = 3 и сделал вывод — данное уравнение корней не имеет. Прав ли учащийся?
2. Решите уравнения, используя взаимосвязь между компонентами и результатами действий:

а) (х + 70) · 4 = 328; в) (85х + 765) :170 = 98;

б) 560: (х + 9) = 56; г) (х -13581):709 = 306.

1. Решите задачи арифметическим и алгебраическим способами:

а) На первой полке на 16 книг больше, чем на второй. Если с каждой полки снять по 3 книги, то на первой полке книг будет в полтора раза больше, чем на второй. Сколько книг на каждой полке?

б) Весь путь от турбазы до станции, равный 26 км, велосипедист проехал за 1 ч 10 мин. Первые 40 мин этого времени он ехал с одной скоростью, а остальное время — со скоростью на 3 км/ч меньше. Най­дите скорость велосипедиста на первом участке пути.

1. Установите, какие из следующих записей являются неравенства­ми с одной переменной:

а) -12 — 7 х 4; д) 17 — 12·8;

в) 17 (13 + 8) 2 + 3х — 4 > 0.

Является ли число 3 решением неравенства 6(2х + 7) 3;

б) и 3х — 1 > 0

б) х 3 — (1 — 2х) является любое действительное число.

Практическое занятие 2.12. Алгебраические операции.

Вопросы и задания для подготовки к занятию:

1. Алгебраическая операция.
2. Свойства операций.
3. Нейтральный и поглощающие элементы.
4. Обратная операция и симметричный элемент.
5. Алгебра (Z₀; +; ).
6. Сформулируйте условия, при которых операция, заданная на множестве Х:

а) будет алгебраической; б) Не будет алгебраической.

1. Объясните, почему сложение и умножение являются алгебраиче­скими операциями на множестве Z целых чисел, а деление не является.
2. На множестве Х = заданы сложение, умножение и вычитание. Являются ли они алгебраическими на этом множестве?
3. Являются ли алгебраическими операции: сложение, умножение, деление и вычитание, заданные на множестве Х, если:

а) Х – множество четных натуральных чисел;

б) Х– множество нечетных натуральных чисел;

в) Х– множество натуральных чисел, кратных 5?

1. Среди следующих высказываний укажите истинные, ответ обоснуйте:

а) Множество N натуральных чисел замкнуто относительно умножения.

б) Множество Q рациональных чисел замкнуто относительно деления (деление на нуль не рассматривается).

в) Множество Z целых чисел замкнуто относительно вычитания и деления.

г) Множество Z целых чисел замкнуто относительно вычитания или деления.

1. Являются ли алгебраическими на множестве натуральных чисел следующие операции:

а) возведение в степень;

б) нахождение наибольшего общего делителя двух чисел;

в) нахождение наименьшего общего кратного двух чисел?

1. Дано множество . Составьте множество Х всех его подмножеств. На этом множестве Х рассмотрите операции пересечения и объединения. Являются ли они алгебраическими?
2. Какие из следующих алгебраических операций в множе­стве целых чисел Z, являются коммутативными: а) сложение; б) вы­читание; в) умножение; г) операция, задаваемая формулой (х, у) →2х — у; д) операция, задаваемая формулой (х, у)→ х 2 — у 2
3. Обладает ли свойством коммутативности: а) операция объединения множеств; б) операция вычитания множеств; в) операция пересе­чения множеств?
4. Какие из следующих алгебраических операций в множе­стве Q рациональных чисел являются коммутативными: а) сложе­ние; б) умножение; в) вычитание; г) операция, задаваемая форму­лой (х, у) → х + 2у; д) операция, задаваемая формулой (х, у) →х 2 + у 2 ?
5. Какие из следующих операций в множестве Z целых чисел ассоциативны: а) сложение; б) вычитание; в) умножение; г) операция (х, у) →х + 2у; д) операция (х, у) →х 2 + у 2 ?
6. Являются ли пересечение и объединение множеств ассоциативными операциями?
7. Является ли ассоциативной операция возведения в сте­пень в множестве натуральных чисел? Проверьте, выполняется ли, например, равенство 2 * (1 * 3)= (2 * 1) * 3, где т* п = тп.
8. Какое число является нейтральным относительно опера­ции сложения целых чисел? Есть ли нейтральный элемент для сложения натуральных чисел?
9. Какое число является нейтральным относительно операции умножения целых чисел?
10. Найдите нейтральный элемент для операции (х, у)→х + у + ху в множестве рациональных чисел.
11. Какое множество является нейтральным элементом относительно операции объединения множеств? Существует ли нейтральный элемент для операции пересечения множеств (рассматриваются лишь подмножества универсального множества U).
12. Является ли деление в множестве положительных чисел дистрибутивным относительно операции сложения?
13. Является ли операция объединения множеств дистрибутивной относительно операции пересечения множеств? Ответ по­ясните с помощью диаграмм Эйлера—Венна.
14. Сократимо ли вычитание и деление на множестве Q?
15. Какое множество является поглощающим элементом относительно операции пересечения множеств?

Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Решение неравенств с одной переменной

Решим неравенство 5х — 5 4; д) 17-12·8;

2.Является ли число 3 решением неравенства 6(2х + 7) 3;

б) x x х 3 — (1 — 2х) является любое действительное число.

7.Докажите, что не существует действительного числа, которое являлось бы решением неравенства 3(2 — х) — 2 > 5 — 3х.

8.Одна сторона треугольника равна 5 см, а другая 8 см. Какой может быть длина третьей стороны, если периметр треугольника:

ГРАФИЧЕСКОЕ РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕН­НОЙ.Для графического решения неравенства f (х) > g (х) нужно построить гра­фики функций

у = f (х) = g (х) и выбрать те проме­жутки оси абсцисс, на которых график функции у = f (х) расположен выше графика функции у = g (х).

Пример 17.8.Решите графически неравенство х 2 — 4 > 3х.

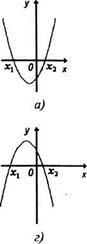
Решение. Построим в одной системе координат графи­ки функций

у = х 2 — 4 и у = Зх (рис. 17.5). Из рисунка видно, что графики функций у = х 2 — 4 расположен выше графика функции у = 3х при х 4, т.е. множество решений исходного неравенства есть множество

(- ¥; -1) È (4; +оо).

Ответ: х Î (- оо; -1) и (4;+ оо ).

Графиком квадратичной функции у = ах 2 + bх + с является парабола с ветвя­ми, направленными вверх, если а > 0, и вниз, если а 2 + bх + с = 0 имеет два различных корня); парабола касается оси х (т.е. уравнение ах 2 + bх + с = 0 имеет один корень); парабола не пересекает ось Ох (т.е. уравнение ах 2 + bх + с = 0 не имеет корней). Таким образом, возможны шесть положений параболы, служа­щей графиком функции у = ах 2 + bх + с (рис. 17.6). Используя эти иллюстрации, можно решать квадратные неравенства.

Пример 17.9. Решите неравенство: а) 2х г + 5х — 3 > 0; б) -Зх 2 — 2х — 6 2 + 5х -3 = 0 имеет два корня: х, = -3, х₂ = 0,5. Парабола, служащая графиком функции у = 2х 2 + 5х -3, показана на рис. а. Неравенство 2х 2 + 5х -3 > 0 выполняется при тех значениях х, при которых точки параболы лежат выше оси Ох: это будет при х х_г> т.е. при х 0,5. Значит, множество решений исходного неравенства есть множество (- ¥; -3) и (0,5; + ¥).

б) Уравнение -Зх 2 + 2х- 6 = 0 не имеет действительных корней. Парабола, служащая графиком функции у = — 3х 2 — 2х — 6, показана на рис. 17.6 Неравенство -3х 2 — 2х — 6 3+х.

Решение. Точки х = 1 и х = 2 делят числовую ось (ОДЗ неравенства (17.9) на три интервала: х 2. Решим данное неравенство на каждом из них. Если х 0; поэтому |х -1| = — (х — I), |2 — х | = 2 — х. Значит, неравенство (17.9) принимает вид: 1- х + 2 — х > 3 + х, т.е. х 3 + х,

х 2, то х — 1 >0 и 2 – х 2,

Объединяя найденные решения на всех частях ОДЗ неравенства (17.9), получаем его решение — множество (-¥; 0) È (6; +оо).

Иногда полезно воспользоваться геометрической интерпретацией модуля действительного числа, согласно которой | а | означает расстояние точки а коор­динатной прямой от начала отсчета О, а | а — b | означает расстояние между точка­ми а и b на координатной прямой. Кроме того, можно использовать метод возве­дения в квадрат обеих частей неравенства.

Теорема 17.5. Если выражения f (х) и g (х) при любых х принимают толь­ко неотрицательные значения, то неравенства f (х) > g (х) и f (х) ² > g (х) ² равносильны.

58. Основные выводы § 12

В данном параграфе мы определили следующие понятия:

— значение числового выражения;

— выражение, не имеющее смысла;

— выражение с переменной (переменными);

— область определения выражения;

— тождественно равные выражения;

— тождественное преобразование выражения;

— уравнение с одной переменной;

— что значит решить уравнение;

— неравенство с одной переменной;

— что значит решить неравенство;

Кроме того, мы рассмотрели теоремы о равносильности уравнений и неравенств, являющиеся основой их решения.

Знание определений всех названных выше понятий и теорем о рав­носильности уравнений и неравенств — необходимое условие методи­чески грамотного изучения с младшими школьниками алгебраическо­го материала.

Дата добавления: 2016-05-11 ; просмотров: 2776 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Практическая работа по ТОНКМ №19

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Практиxеская работа (неравенства с одной переменной)

Задание 1. Установите, какие из следующих записей являются неравенствами с одной переменной:

Задание 2. Является ли число 4 решением неравенства 6(2х-7) R ?

Ответ: число 4 является решением неравенства

Задание 3. Равносильны ли на множестве действительных чисел следующие пары неравенств:

а) 16х  64 и х  4

Задание 4. Решите неравенство 3(х+2)-4(х-1)2(х+3)-2 и обоснуйте все преобразования, которые будете при этом выполнять.

Раскроем скобки неравенства

Перенесем выражение 2х в левую часть, а 6 и -4 в правую, поменяв знаки на противоположные:

Воспользовались следствием вторым из теоремы 1. Получили неравенство, равносильное исходному

Приведем подобные члены в левой и правой частях неравенства:

Выполнили тождественные преобразования выражений в левой и правой частях неравенства – они не нарушили равносильности неравенства исходного и данного

Разделим обе части неравенства на -3:

Воспользовались следствием из теоремы 2, получили неравенство, равносильное исходному.

Задание 5. Одна сторона треугольника равна 5см, другая 5см. какой может быть длина третьей стороны, если периметр треугольника меньше 21см?

Пусть третья сторона х см, тогда 5+8+х  21. У треугольника сумма двух сторон больше третьей стороны х+5 8

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 75 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 861 человек из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 51 человек из 23 регионов

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 841 738 материалов в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 03.11.2019
• 2257
• 252

• 03.11.2019
• 640
• 58

• 03.11.2019
• 212
• 3

• 03.11.2019
• 837
• 6

• 03.11.2019
• 137
• 1

• 03.11.2019
• 459
• 12

• 03.11.2019
• 231
• 0

• 03.11.2019
• 304
• 1

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 03.11.2019 509
• DOCX 15.3 кбайт
• 3 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Платонова Яна Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 3 года и 9 месяцев
• Подписчики: 1
• Всего просмотров: 163148
• Всего материалов: 117

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минобрнауки отменило плановые и внеплановые проверки вузов в 2022 году

Время чтения: 1 минута

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Около 20% детей до 15 лет не воспринимают прочитанную информацию

Время чтения: 1 минута

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Госдума рассматривает проект о регулировании «продленок» в школах

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🔥 Видео

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

ОГЭ по математике. Решаем уравнения | МатематикаСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

Уравнения с модулем. Часть 2 | Математика | TutorOnlineСкачать

Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Уравнения с модулемСкачать

Неравенства с модулем | Математика | TutorOnlineСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

7 класс. Линейные уравнения с одной переменнойСкачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Решение задач с помощью уравнений.Скачать