Условия перпендикулярности прямых на плоскости для различных видов уравнений (7 видео)

Перпендикулярные прямые, условие перпендикулярности прямых.

В этой статье подробно рассмотрим перпендикулярные прямые на плоскости и в трехмерном пространстве. Начнем с определения перпендикулярных прямых, покажем обозначения и приведем примеры. После этого приведем необходимое и достаточное условие перпендикулярности двух прямых и детально разберем решения характерных задач.

Навигация по странице.

Содержание

Перпендикулярные прямые – основные сведения.
Перпендикулярность прямых — условия перпендикулярности.
Различные виды уравнений прямой на плоскости. Угол между прямыми. Условие параллельности и перпендикулярности прямых
Перпендикулярные прямые, условие перпендикулярности прямых
Перпендикулярные прямые – основные сведения
Перпендикулярность прямых – условия перпендикулярности
💡 Видео

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Перпендикулярные прямые – основные сведения.

Угол между пересекающимися прямыми на плоскости и в трехмерном пространстве может быть равен девяноста градусам. В этом случае говорят, что прямые пересекаются под прямым углом, а прямые называют перпендикулярными. Если угол между скрещивающимися прямыми в трехмерном пространстве равен , то скрещивающиеся прямые также называют перпендикулярными. Таким образом, перпендикулярные прямые на плоскости являются пересекающимися, перпендикулярные прямые в пространстве могут быть как пересекающимися, так и скрещивающимися.

Отметим, что фразы «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» равноправны. Поэтому можно слышать, что перпендикулярные прямые называют взаимно перпендикулярными.

Учитывая все сказанное, дадим общее определение перпендикулярных прямых.

Две прямые называются перпендикулярными, если угол между ними равен .

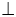
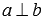
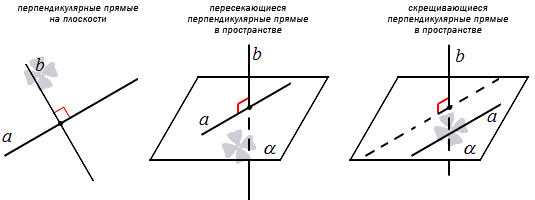
Для обозначения перпендикулярных прямых используют знак перпендикулярности вида «». То есть, если прямые a и b перпендикулярны, то кратко записывают . На чертежах угол между перпендикулярными прямыми отмечают значком прямого угла вида «».

В качестве примера перпендикулярных прямых на плоскости можно привести прямые, на которых лежат стороны квадрата с общей вершиной. В прямоугольной системе координат Oxyz в трехмерном пространстве координатные прямые Ox и Oz , Ox и Oy , Oy и Oz перпендикулярны.

Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Перпендикулярность прямых — условия перпендикулярности.

Перпендикулярные прямые фигурируют чуть ли не в каждой геометрической задаче. Иногда перпендикулярность прямых известна из условия, а в других случаях перпендикулярность прямых приходится доказывать. Для доказательства перпендикулярности двух прямых достаточно показать, используя любые геометрические методы, что угол между прямыми равен девяноста градусам.

А как ответить на вопрос «перпендикулярны ли прямые», если известны уравнения, задающие эти прямые в прямоугольной системе координат на плоскости или в трехмерном пространстве?

Для этого следует воспользоваться необходимым и достаточным условием перпендикулярности двух прямых. Сформулируем его в виде теоремы.

Для перпендикулярности прямых a и b необходимо и достаточно, чтобы направляющий вектор прямой a был перпендикулярен направляющему вектору прямой b .

Доказательство этого условия перпендикулярности прямых основано на определении направляющего вектора прямой и на определении перпендикулярных прямых.

Пусть на плоскости введена прямоугольная декартова система координат Oxy и заданы уравнения прямой на плоскости некоторого вида, определяющие прямые a и b . Обозначим направляющие векторы прямых а и b как и соответственно. По уравнениям прямых a и b можно определить координаты направляющих векторов этих прямых – получаем и . Тогда, для перпендикулярности прямых a и b необходимо и достаточно, чтобы выполнялось условие перпендикулярности векторов и , то есть, чтобы скалярное произведение векторов и равнялось нулю: .

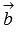
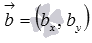
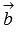
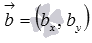
Итак, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxy на плоскости имеет вид , где и — направляющие векторы прямых a и b соответственно.

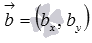
Это условие удобно использовать, когда легко находятся координаты направляющих векторов прямых, а также когда прямым a и b соответствуют канонические уравнения прямой на плоскости или параметрические уравнения прямой на плоскости.

В прямоугольной системе координат Oxy заданы три точки . Перпендикулярны ли прямые АВ и АС ?

Векторы и являются направляющими векторами прямых АВ и АС . Обратившись к статье координаты вектора по координатам точек его начала и конца, вычисляем . Векторы и перпендикулярны, так как . Таким образом, выполняется необходимое и достаточное условие перпендикулярности прямых АВ и АС . Следовательно, прямые АВ и АС перпендикулярны.

да, прямые перпендикулярны.

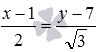
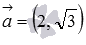
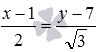
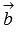
Являются ли прямые и перпендикулярными?

— направляющий вектор прямой , а — направляющий вектор прямой . Вычислим скалярное произведение векторов и : . Оно отлично от нуля, следовательно, направляющие векторы прямых не перпендикулярны. То есть, не выполняется условие перпендикулярности прямых, поэтому, исходные прямые не перпендикулярны.

нет, прямые не перпендикулярны.

Аналогично, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxyz в трехмерном пространстве имеет вид , где и — направляющие векторы прямых a и b соответственно.

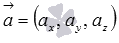
Перпендикулярны ли прямые, заданные в прямоугольной системе координат Oxyz в трехмерном пространстве уравнениями и ?

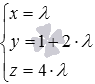
Числа, стоящие в знаменателях канонических уравнений прямой в пространстве, являются соответствующими координатами направляющего вектора прямой. А координатами направляющего вектора прямой, которая задана параметрическими уравнениями прямой в пространстве, являются коэффициенты при параметре. Таким образом, и — направляющие векторы заданных прямых. Выясним, перпендикулярны ли они: . Так как скалярное произведение равно нулю, то эти векторы перпендикулярны. Значит, выполняется условие перпендикулярности заданных прямых.

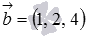
Для проверки перпендикулярности двух прямых на плоскости существуют другие необходимые и достаточные условия перпендикулярности.

Для перпендикулярности прямых a и b на плоскости необходимо и достаточно, чтобы нормальный вектор прямой a был перпендикулярен нормальному вектору прямой b .

Озвученное условие перпендикулярности прямых удобно использовать, если по заданным уравнениям прямых легко находятся координаты нормальных векторов прямых. Этому утверждению отвечает общее уравнение прямой вида , уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом .

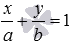
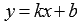
Убедитесь, что прямые и перпендикулярны.

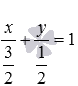
По заданным уравнениям прямых легко найти координаты нормальных векторов этих прямых. – нормальный вектор прямой . Перепишем уравнение в виде , откуда видны координаты нормального вектора этой прямой: .

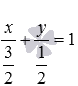
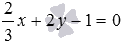
Векторы и перпендикулярны, так как их скалярное произведение равно нулю: . Таким образом, выполняется необходимое и достаточное условие перпендикулярности заданных прямых, то есть, они действительно перпендикулярны.

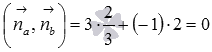
В частности, если прямую a на плоскости определяет уравнение прямой с угловым коэффициентом вида , а прямую b – вида , то нормальные векторы этих прямых имеют координаты и соответственно, а условие перпендикулярности этих прямых сводится к следующему соотношению между угловыми коэффициентами .

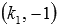
Перпендикулярны ли прямые и ?

Угловой коэффициент прямой равен , а угловой коэффициент прямой равен . Произведение угловых коэффициентов равно минус единице , следовательно, прямые перпендикулярны.

заданные прямые перпендикулярны.

Можно озвучить еще одно условие перпендикулярности прямых на плоскости.

Для перпендикулярности прямых a и b на плоскости необходимо и достаточно, чтобы направляющий вектор одной прямой и нормальный вектор второй прямой были коллинеарны.

Этим условием, очевидно, удобно пользоваться, когда легко находятся координаты направляющего вектора одной прямой и координаты нормального вектора второй прямой, то есть, когда одна прямая задана каноническим уравнением или параметрическими уравнениями прямой на плоскости, а вторая – или общим уравнением прямой, или уравнением прямой в отрезках, или уравнением прямой с угловым коэффициентом.

Являются ли прямые и перпендикулярными?

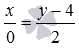
Очевидно, — нормальный вектор прямой , а — направляющий вектор прямой . Векторы и не коллинеарны, так как для них не выполняется условие коллинеарности двух векторов (не существует такого действительного числа t , при котором ). Следовательно, заданные прямые не перпендикулярны.

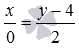
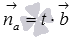
Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Различные виды уравнений прямой на плоскости. Угол между прямыми. Условие параллельности и перпендикулярности прямых

1) Общим уравнение прямой на плоскости называется уравнение вида:

перпендикулярный прямой называется нормальным вектором прямой.

2) Уравнение прямой с угловым коэффициентом:

Пусть означает угол наклона прямой к оси . Тогда называется угловым коэффициентом прямой. Значение есть ордината точки пересечения прямой с осью . Если прямую задать угловым коэффициентом и какой-нибудь её точкой, то прямая может быть задана уравнением .

3) Уравнение прямой в отрезках

Числа равны длинам отрезков, которые отсекает прямая на осях координат.

4) Уравнение прямой, проходящей через данную точку и перпендикулярно данному вектору.

Пусть — точка, принадлежащая прямой; — нормальный вектор этой прямой, тогда уравнение прямой имеют вид

5) Каноническое уравнение прямой.

Пусть задана точка , принадлежащая искомой прямой, и вектор , коллинеарный этой прямой. Тогда каноническое уравнение прямой имеет вид . Вектор называется направляющий вектор прямой.

6) Уравнение прямой, проходящей через две заданные точки.

Рассмотрим прямую, проходящую через точки и .

Уравнение прямой имеет вид

Найти общее уравнение прямой l , проходящей через точку и параллельной прямой

Решение. Примем нормальный вектор данной прямой в качестве нормального вектора искомой и запишем уравнение в виде:

Ответ: общее уравнение прямой l имеет вид .

Найти общее уравнение прямой , проходящей через точку и перпендикулярно прямой

Решение. Так как нормальный вектор данной прямой является направляющим вектором для перпендикулярной ей прямой, то искомое уравнение можно записать в канонической форме:

Ответ: общее уравнение прямой l имеет вид

Составить уравнение прямой l, проходящей через точку и отсекающую оси отрезок, равный 7.

Решение. Найдём координаты второй точки, через которую проходит прямая — это пересечения с осью . Координаты этой точки. Тогда, в соответствии с формулой прямой, проходящей через 2 точки будем иметь:

Ответ: общее уравнение прямой l имеет вид.

7) Угол между прямыми, заданными уравнениями с угловыми коэффициентами.

Тогда угол между ними вычисляется по формуле: ;

Условие параллельности прямых и имеет вид: ;

Условие их перпендикулярности: ;

8) Угол между прямыми, заданными уравнениями в общем виде. Если прямые и заданы общими уравнениями:

(нормальный вектор этой прямой )

(нормальный вектор этой прямой ). .

Условие параллельности прямых и :

Условие их перпендикулярности:

Пример. Найти угол между прямыми и

Решение. Координаты нормальных векторов прямых определим из их уравнений: и Найдём косинус между прямыми:

Ответ: угол между прямыми

9) Расстояние от точки до прямой определяется по формуле:

Найти расстояние между параллельными прямыми:

Решение. Возьмём на первой прямой произвольную точку . Пусть, например, , тогда , т.е. : по формуле находим расстояние от точки до второй прямой:

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Перпендикулярные прямые, условие перпендикулярности прямых

В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Перпендикулярные прямые – основные сведения

Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.

То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.

Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.

Перпендикулярность обозначается « ⊥ », а запись принимает вид a ⊥ b , что значит, прямая a перпендикулярна прямой b .

Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной. В трехмерном пространстве прямые O x , O z , O y перпендикулярны попарно: O x и O z , O x и O y , O y и O z .

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Перпендикулярность прямых – условия перпендикулярности

Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.

Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.

Для того, чтобы прямые a и b были перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b .

Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.

Пусть введена прямоугольная декартова система координат О х у с заданными уравнениями прямой на плоскости, которые определяют прямые a и b . Направляющие векторы прямых a и b обозначим a → и b → . Из уравнения прямых a и b необходимым и достаточным условием является перпендикулярность векторов a → и b → . Это возможно только при скалярном произведении векторов a → = ( a x , a y ) и b → = ( b x , b y ) равном нулю, а запись имеет вид a → , b → = a x · b x + a y · b y = 0 . Получим, что необходимым и достаточным условием перпендикулярности прямых a и b , находящихся в прямоугольной системе координат О х у на плоскости, является a → , b → = a x · b x + a y · b y = 0 , где a → = ( a x , a y ) и b → = b x , b y — это направляющие векторы прямых a и b .

Условие применимо, когда необходимо найти координаты направляющих векторов или при наличии канонических или параметрических уравнений прямых на плоскости заданных прямых a и b .

Заданы три точки A ( 8 , 6 ) , B ( 6 , 3 ) , C ( 2 , 10 ) в прямоугольной системе координат О х у . Определить, прямые А В и А С перпендикулярны или нет.

Прямые А В и А С имеют направляющие векторы A B → и A C → соответственно. Для начала вычислим A B → = ( — 2 , — 3 ) , A C → = ( — 6 , 4 ) . Получим, что векторы A B → и A C → перпендикулярны из свойства о скалярном произведении векторов, равном нулю.

A B → , A C → = ( — 2 ) · ( — 6 ) + ( — 3 ) · 4 = 0

Очевидно, что необходимое и достаточное условие выполнимо, значит, А В и А С перпендикулярны.

Ответ: прямые перпендикулярны.

Определить, заданные прямые x — 1 2 = y — 7 3 и x = 1 + λ y = 2 — 2 · λ перпендикулярны или нет.

Решение

a → = ( 2 , 3 ) является направляющим вектором заданной прямой x — 1 2 = y — 7 3 ,

b → = ( 1 , — 2 ) является направляющим вектором прямой x = 1 + λ y = 2 — 2 · λ .

Перейдем к вычислению скалярного произведения векторов a → и b → . Выражение будет записано:

a → , b → = 2 · 1 + 3 · — 2 = 2 — 6 ≠ 0

Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.

Ответ: прямые не перпендикулярны.

Необходимое и достаточное условие перпендикулярности прямых a и b применяется для трехмерного пространства, записывается в виде a → , b → = a x · b x + a y · b y + a z · b z = 0 , где a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b .

Проверить перпендикулярность прямых в прямоугольной системе координат трехмерного пространства, заданные уравнениями x 2 = y — 1 = z + 1 0 и x = λ y = 1 + 2 · λ z = 4 · λ

Знаменатели из канонических уравнений прямых считаются координатами направляющего вектора прямой. Координаты направляющего вектора из параметрического уравнения – коэффициенты. Отсюда следует, что a → = ( 2 , — 1 , 0 ) и b → = ( 1 , 2 , 4 ) являются направляющими векторами заданных прямых. Для выявления их перпендикулярности найдем скалярное произведение векторов.

Выражение примет вид a → , b → = 2 · 1 + ( — 1 ) · 2 + 0 · 4 = 0 .

Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.

Ответ: прямые перпендикулярны.

Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.

Прямые a и b на плоскости считаются перпендикулярными при перпендикулярности нормального вектора прямой a с вектором b , это и есть необходимое и достаточное условие.

Данное условие применимо, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. То есть при наличии общего уравнения прямой вида A x + B y + C = 0 , уравнения прямой в отрезках вида x a + y b = 1 , уравнения прямой с угловым коэффициентом вида y = k x + b координаты векторов возможно найти.

Выяснить, перпендикулярны ли прямые 3 x — y + 2 = 0 и x 3 2 + y 1 2 = 1 .

Исходя их уравнений, необходимо найти координаты нормальных векторов прямых. Получим, что n α → = ( 3 , — 1 ) — это нормальный вектор для прямой 3 x — y + 2 = 0 .

Упростим уравнение x 3 2 + y 1 2 = 1 до вида 2 3 x + 2 y — 1 = 0 . Теперь четко видны координаты нормального вектора, которые запишем в такой форме n b → = 2 3 , 2 .

Векторы n a → = ( 3 , — 1 ) и n b → = 2 3 , 2 будут перпендикулярными, так как их скалярное произведение даст в итоге значение равное 0 . Получим n a → , n b → = 3 · 2 3 + ( — 1 ) · 2 = 0 .

Необходимое и достаточное условие было выполнено.

Ответ: прямые перпендикулярны.

Когда прямая a на плоскости определена при помощи уравнения с угловым коэффициентом y = k 1 x + b 1 , а прямая b — y = k 2 x + b 2 , отсюда следует, что нормальные векторы будут иметь координаты ( k 1 , — 1 ) и ( k 2 , — 1 ) . Само условие перпендикулярности сводится к k 1 · k 2 + ( — 1 ) · ( — 1 ) = 0 ⇔ k 1 · k 2 = — 1 .

Выяснить, перпендикулярны ли прямые y = — 3 7 x и y = 7 3 x — 1 2 .

Прямая y = — 3 7 x имеет угловой коэффициент, равный — 3 7 , а прямая y = 7 3 x — 1 2 — 7 3 .

Произведение угловых коэффициентов дает значение — 1 , — 3 7 · 7 3 = — 1 , то есть прямые являются перпендикулярными.

Ответ: заданные прямые перпендикулярны.

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.

Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.

Определить, являются ли заданные прямые x — y — 1 = 0 и x 0 = y — 4 2 перпендикулярными.

Получаем, что нормальный вектор прямой x — y — 1 = 0 имеет координаты n a → = ( 1 , — 1 ) , а b → = ( 0 , 2 ) — направляющий вектор прямой x 0 = y — 4 2 .

Отсюда видно, что векторы n a → = ( 1 , — 1 ) и b → = ( 0 , 2 ) не коллинеарны, потому что условие коллинеарности не выполняется. Не существует такого числа t , чтобы выполнялось равенство n a → = t · b → . Отсюда вывод, что прямые не являются перпендикулярными.