Впервые существование решения дифференциального уравнения было доказано Коши. Приводимое ниже доказательство основано на методе последовательных приближений, который принадлежит Пикару. Этот метод имеет самостоятельное значение, поскольку позволяет получить приближенное решение дифференциального уравнения.
- Формулировка теоремы
- Условие Липшица
- Доказательство существования решения
- 1) Доказательство существования предела yn при n стремящемся к бесконечности
- 2) Доказательство того, что Y является решением (4)
- Доказательство единственности решения
- Условия однозначности
- Обыкновенные дифференциальные уравнения
- Обыкновенные дифференциальные уравнения
- Основные понятия о дифференциальных уравнениях
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения с разделенными переменными
- Дифференциальные уравнения с разделяющимися переменными
- Однородные дифференциальные уравнения
- Линейные дифференциальные уравнения
- Дифференциальное уравнение Бернулли
- Обыновенное дефференциальное уравнение
- Основные понятия и определения
- Примеры с решением
- Системы обыкновенных дифференциальных уравнений
- Системы дифференциальных уравнений первого порядка
- Системы линейных дифференциальных уравнений с постоянными коэффициентами
- 📺 Видео
Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Формулировка теоремы
Пусть дано дифференциальное уравнение первого порядка:
(1)
с начальным условием
(1.1) .
Пусть – непрерывная функция двух переменных в замкнутой области :
и, следовательно, ограничена некоторым положительным значением :
(2) .
И пусть функция удовлетворяет условию Липшица:
(3) ,
.
Тогда существует единственное решение уравнения (1):
,
удовлетворяющее начальному условию , определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .
Условие Липшица
Рассмотрим условие Липшица. Оно имеет вид:
(3) ,
где – положительное число;
, и – любые значения из области :
, , .
Смысл условия Липшица легко понять, если записать его в виде:
(3.1) .
При некотором фиксированном значении переменной , функция является функцией от переменной : . Пусть мы имеем график этой функции. Возьмем две точки, принадлежащие , на этом графике и проведем через них прямую. Тогда угол между прямой и осью ограничен некоторым значением , которое меньше . При таком ограничении график не имеет вертикальных касательных и скачков. А в тех точках, где существует частная производная , она ограничена:
.
Если в области функция имеет непрерывную частную производную , то в этой области выполняется условие Липшица (3).
Для доказательства заметим, что поскольку частная производная непрерывна в замкнутой области, то она ограничена:
.
По теореме Лагранжа о конечных приращениях, имеем:
,
где частные производные вычисляются в некоторой точке , в которой переменная принадлежат интервалу между и :
.
Тогда:
.
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Доказательство существования решения
Приведем исходное уравнение (1) с начальным условием (1.1) к интегральному уравнению. Левая и правая части (1) являются функциями от . Заменим на :
.
Интегрируем это уравнение по от до :
;
Подставим начальное условие . В результате получим интегральное уравнение:
(4) .
Покажем, что интегральное уравнение (4) эквивалентно дифференциальному уравнению (1) с начальным условием (1.1). Для этого нужно показать, что из (1) и (1.1) следует (4) и из (4) следует (1) и (1.1). То, что из (1) и (1.1) следует (4) мы уже показали. Осталось показать, что из (4) следует (1) и (1.1). Для этого подставим в (4) . Получим начальное условие (1.1). Продифференцировав обе части уравнения (4) по , получаем уравнение (1).
Далее мы пытаемся найти решение уравнения (4) с помощью последовательных приближений. Для этого определяем ряд функций от переменной по формулам:
(5.1) ;
(5.2) ;
(5.3) ;
.
(5.n) .
Мы предполагаем, что при , стремится к решению уравнения (4):
(6) ,
где – решение уравнения (4). Если мы докажем это, то мы докажем существование решения.
Доказательство существования решения будем проводить в два этапа:
1> вначале докажем, что предел (6) существует;
2) затем докажем, что удовлетворяет уравнению (4):
.
1) Доказательство существования предела yn при n стремящемся к бесконечности
Сведем последовательные приближения (5.1) – (5.n) к сумме ряда. Для этого пишем:
.
Таким образом нам нужно доказать, что ряд
(7)
сходится при .
Сначала покажем, что при , последовательные приближения принадлежат интервалу .
Действительно, при имеем:
.
Поскольку есть наименьшее из двух чисел и , то и
.
Далее, поскольку принадлежит интервалу , то . Тогда, аналогично предыдущему,
.
Отсюда
.
Далее, по индукции, поскольку принадлежат интервалу , то и
.
Отсюда
.
Итак, мы доказали, что последовательные приближения принадлежат интервалу
.
Теперь мы можем оценить члены ряда (7), применяя условие Липшица.
Для первого члена имеем:
;
(8.1) .
Для второго члена применяем условие Липшица и оценку (8.1):
;
(8.2) .
Для третьего члена применяем, аналогично, условие Липшица и оценку (8.2):
;
(8.3) .
Далее применим метод индукции. Пусть
(8.n) .
Тогда
;
(8.n+1) .
Итак, поскольку (8.n) справедливо для и из (8.n) следует (8.n+1), то (8.n) выполняется для любых .
Запишем ряд (7) в виде:
(7.1) ,
где .
Применим (8.n) и заменим наибольшим допустимым значением :
.
Тогда каждый член ряда (7.1) ограничен по модулю членом ряда
(9) .
Исследуем ряд (9) на сходимость. Применим признак Даламбера:
.
Итак, ряд (9) сходится. Поскольку все члены ряда (7.1), начиная со второго, по абсолютной величине меньше членов сходящегося ряда (9), то, в силу критерия Вейерштрасса, ряд (7.1) сходится равномерно для всех , удовлетворяющих условию . Поскольку интеграл есть непрерывная функция от верхнего предела, то каждый член ряда (7.1) есть непрерывная функция от . Поэтому предел
(10)
существует и является непрерывной функцией от .
2) Доказательство того, что Y является решением (4)
Рассмотрим уравнение (5.n):
(5.n) .
Докажем, что при , это уравнение стремится к уравнению
(11) .
В силу (10) левая часть уравнения (5.n) стремится к .
Теперь покажем, что
.
Перепишем правую часть (5.n):
.
Далее заметим, что поскольку все принадлежат закрытому интервалу , то и принадлежит этому интервалу, . Поэтому мы можем применить условие Липшица.
Оценим абсолютную величину последнего члена:
.
Поскольку, при , стремится к равномерно, то для любого положительного числа можно указать такое натуральное число , что для всех ,
.
Тогда
.
Поскольку произвольно, то
Поэтому
.
То есть при уравнение
(5.n)
принимает вид
(11) .
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Доказательство единственности решения
Предположим, что уравнение
(4)
имеет два решения и , различающиеся в некоторой точке , принадлежащей интервалу .
Рассмотрим функцию
.
Будем считать, что . В противном случае поменяем местами и .
Поскольку и непрерывны, то и непрерывная функция. Поэтому она отлична от нуля в некотором интервале, содержащем точку :
при .
Поскольку , то . То есть точка не принадлежит этому интервалу.
Если , то преобразуем (4) следующим образом:
,
где
.
Если переобозначить постоянные
,
то получим задачу (4), для которой
;
при ,
где – некоторое число, не превосходящее .
Если , то поступаем аналогично:
,
Переобозначим постоянные:
.
Получаем задачу (4), для которой
;
при ,
где – некоторое число, не меньшее .
Итак, мы имеем:
;
при ( или при ).
Далее возьмем произвольное положительное число ( или ) и рассмотрим закрытый интервал ( или ). Поскольку функция непрерывна, то она достигает наибольшего значения в одной из точек этого интервала:
( или ).
Сделаем оценку, применяя уравнение (4) и условие Липшица:
;
.
Поскольку , то разделим на :
.
Возникает противоречие, поскольку при это неравенство не выполняется.
Следовательно, не может иметь отличных от нуля значений. Поэтому . Что и требовалось доказать.
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Автор: Олег Одинцов . Опубликовано: 04-06-2016 Изменено: 20-06-2016
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Условия однозначности
В самом общем виде процесс переноса теплоты теплопро-водностью и конвекцией описывается уравнением Фурье-Кирхгофа, которое для одномерного движения имеет вид:
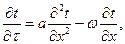
где 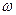
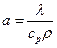
Коэффициент температуропроводности характеризует скорость изменения температуры внутри тела (среды), т.е. меру его инерционности и определяет способность среды проводить теплоту теплопроводностью.
Процесс теплопроводности внутри твердого тела без внутренних источников теплоты в одномерном случае (плоская бесконечная стенка) описывается уравнением ( 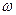
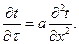
При конвективном теплообмене (конвекция совместно с теплопроводностью) кроме уравнения Фурье-Кирхгофа рассматриваются также дифференциальные уравнения Навье-Стокса, уравнение сплошности и уравнение теплообмена на границе раздела.
Уравнение Навье-Стокса для одномерного движения газа (вдоль оси Х):
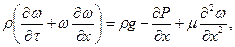
где r — плотность, кг/м 3 ;
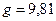
Р — давление, H/м 2 (Па);
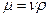
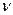
Все слагаемые уравнения имеет размерность силы, отнесенной к единице объема. Левая часть уравнения характеризует инерционные силы (в скобках — ускорение элементарной массы газа).
В правой части первый член характеризует силы тяжести, второй — силы давления и третий — силы вязкости. Эти три составляющие определяют сумму сил, действующих на элементарный объем газа.
Уравнение сплошности (выражает принцип постоянства массового расхода газа):
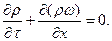
Уравнение на границе теплообмена:
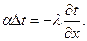
Для получения конкретного решения уравнений (43) — (47) необходимо задать условия однозначности или краевые условия. Условия однозначности включают:
1. геометрические условия, которые дают сведения о форме и размерах тела;
2. физические условия, включающие такие свойства, как теплопроводность l, теплоемкость cp, плотность r, температуропроводность 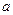
3. начальные условия, которые характеризуют распределение температуры в теле (среде) в начале процесса; при стационарном тепловом режиме начальные условия не задаются;
4. граничные условия, которые дают сведения об условиях теплообмена на поверхности тела (на границе между окружающей средой и поверхностью).
Граничные условия бывают четырёх родов и задаются соответственно способу нагревания или охлаждения тела.
Граничные условия первого рода характеризуются заданием температуры поверхности тела как функции времени и координат:
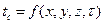
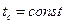
Граничные условия второго рода характеризуются заданием теплового потока, поступающего на поверхность тела, как функции времени и координат:
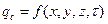
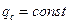
При граничных условиях третьего рода задается зависимость плотности теплового потока вследствие теплопроводности со стороны тела от температур поверхности тела 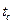
В общем виде граничные условия третьего рода задаются как
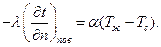
Если теплота на поверхность тела передается конвекцией, то тепловой поток определяется по уравнению (39), а если излучением – по уравнению (41).
Возможен случай передачи теплоты одновременно излучением и конвекцией
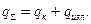
Используя уравнения (39) и (41), его можно записать в следующем виде:
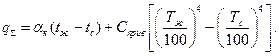
Разделив и умножив оба члена уравнения на разность температур 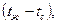
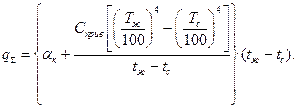
Из формулы (54) следует, что суммарный коэффициент теплоотдачи при переносе теплоты конвекцией и излучением составит
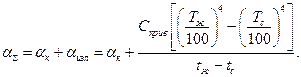
При граничных условиях четвертого рода два тела находятся в плотном контакте между собой. Передача теплоты осуществляется теплопроводностью. В этом случае выполняется равенство температур на границе и тепловых потоков по обе стороны от границы раздела:
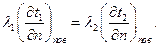
Дифференциальные уравнения (43) или (44) с заданными условиями однозначности дают полную математическую формулировку краевой задачи теплопроводности. Решение задачи осуществляется аналитическими, численными и экспериментальными методами с привлечением теории подобия и моделирования.
Дата добавления: 2015-02-13 ; просмотров: 1818 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Общее и частное решение дифференциального уравненияСкачать

Обыкновенные дифференциальные уравнения
Содержание:
Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Обыкновенные дифференциальные уравнения
При решении многих задач математики, техники, экономики и других отраслей науки бывает трудно установить закон, связывающий искомые и известные переменные величины. Но удается установить связь между производными или дифференциалами этих переменных, которая выражается уравнениями или системами уравнений. Такие уравнения называют дифференциальными уравнениями. Термин «дифференциальное уравнение» введен в 1676 году В. Лейбницом.
Мы рассмотрим только уравнения с функциями одной переменной и обычными производными, которые называют обычными дифференциальными уравнениями.
Основные понятия о дифференциальных уравнениях
Определение. Дифференциальным уравнением называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и еепроизводные или дифференциалы разных порядков, то есть уравнение

Важно понять, что искомая функция в дифференциальном уравнении входит под знак дифференциала или под знак производной.
Определение. Порядком дифференциального уравнения называется наивысший порядок производной от неизвестной функции, входящей в дифференциальное уравнение.
Так, уравнение y’ – 2 xy 2 + 5 = 0 является дифференциальным уравнением первого порядка, а уравнения y» + 2 y’ – y – sin x = 0 — дифференциальным уравнением второго порядка.
Определение. Решением дифференциального уравнения (7.1) называется такая функция y = φ (x), которая при подстановке в уравнение (7.1) превращает его в тождество.
Например, для дифференциального уравнения
y’- 2 x = 0 (7.2)
решением является функция y = x 2 . Найдем производную y’= 2x и подставим в уравнение, получим: 2x – 2x = 0, 0 ≡ 0.
Следует заметить, что y = x 2 не единственное решение уравнения. Это уравнение имеет бесконечное множество решений, которые можно записать так: y = x 2 + C.
Дифференциальные уравнения первого порядка
Определение. Дифференциальным уравнением первого порядка называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и ее первую производную:
F (x, y, y’) = 0. (7.3)
Поскольку производную можно записать в виде отношения дифференциалов, то в уравнение производная может не входить, а будут входить дифференциалы неизвестной функции и независимой переменной.
Если уравнение (7.2) решить относительно у’, то оно будет иметь вид:
y’= f (x, y) или 
Простые примеры показывают, что дифференциальное уравнение может иметь бесконечное множество решений. Это мы видим на примере уравнения (7.2). Легко убедиться также, что дифференциальное уравнение 


Как видим, в решение указанных дифференциальных уравнений входит произвольное число C. Предоставляя постоянной C различные значения, будем получать различные решения дифференциального уравнения.
Определение. Общим решением дифференциального уравнения (7.3) называется функция
у = φ (х, С), (7.5)
которая зависит от одной произвольной постоянной и удовлетворяет дифференциальное уравнение при произвольном значении C.
Если функция (7.5) выражается неявно, то есть в виде
Ф (х, у, С) = 0, (7.6)
то (7.6) называется общим интегралом дифференциального уравнения.
Определение. Частным решением дифференциального уравнения (7.3) называется такое решение, которое получается из общего решения (7.5) при некотором конкретном значении постоянной C.
Ф (х, у, С0) называется частным интегралом дифференциального уравнения.
На практике при решении конкретных задач часто приходится находить не все решения, а решение, которое удовлетворяет определенным начальным условиям. Одной из таких задач является задача Коши, которая для дифференциального уравнения первого порядка формулируется так: среди всех решений дифференциального уравнения (7.3) найти такое решение y, которое при заданном значении независимой переменной x = x0 равна заданному значению y0 , то есть y (x0) = y0 или 
Условие (7.7) называется начальным условием решения.
Покажем на примере, как найти частное решение дифференциального уравнения, когда известно общее решение и задано начальное условие.
Мы видим, что дифференциальное уравнение 

Ответ на вопрос о том, при каких условиях уравнение (7.4) имеет
решение, дает теорема Коши.
ТЕОРЕМА (о существовании и единственности решения). Если функция f (x, y) и ее частная производная 
Теорема Коши дает достаточные условия существования единого решения дифференциального уравнения (7.4). Заметим, что в условии теоремы не требуется существования частной производной 
График произвольного частного решения дифференциального уравнения называется интегральной кривой. Общему решению отвечает семья кривых. Так мы проверили, что уравнение 
которые проходят через начало координат (рис. 1).
Уравнение 
Если задано начальное условие 
интегральных кривых мы выбираем проходящую через точку M0 (x0; y0).
Надо заметить, что нахождение решения дифференциального уравнения часто называют интегрированием уравнения. При этом операцию интегрирования функций называют квадратурой.
Общего метода решения дифференциальных уравнений первого порядка не существует. Рассмотрим некоторые методы решения отдельных типов дифференциальных уравнений.
Дифференциальные уравнения с разделенными переменными
Определение. Уравнение вида
f1 (y) dy = f2 (x) dx, (7.8)
где f1 (y) и f2 (x) — заданные функции, называется дифференциальным уравнением с разделенными переменными.
В этом уравнении каждая из переменных находится только в той части уравнения, где находится ее дифференциал. Уравнение dy = f (x) dx является частным случаем уравнения (7.8). Чтобы решить уравнение (7.8), надо проинтегрировать обе его части: 
Понятно, что произвольную постоянную С можно записывать в любой части равенства.
Пример 1. Решить дифференциальное уравнение: 
Решение. Проинтегрируем левую и правую части уравнения, причем для удобства потенцирования, произвольную постоянную запишем в виде ln |C| получим: 


Подставляя в общее решение начальное условие, найдем С: 2 = С.
Итак,

Дифференциальные уравнения с разделяющимися переменными
Определение. Уравнение вида
f1 (x) f2 (y) + g1 (x) g2 (y) = 0 (7.9)
называется дифференциальным уравнением с разделяющимися переменными.
В этом уравнении переменные еще не разделены, но, поделив обе части уравнения на произведение f2 (y) g1 (x), получим уравнение с разделенными переменными:
Интегрируя это уравнение, запишем 
Получили общий интеграл данного уравнения.
Пример 2. Решить дифференциальное уравнение
x (y + 1) dx – (x 2 + 1) ydy = 0.
Решение. Поделим обе части этого уравнения на (y + 1) (x 2 + 1), после чего получим 
Интегрируя, получим



Пример 3. Найти частное решение дифференциального уравнения (1 + x 2 ) dy + ydx = 0, удовлетворяющее начальному условию y (0) = 1.
Решение. Отделим переменные, поделив уравнение на y ⋅ (1 + x 2 ), и проинтегрируем данное уравнение:
Получили общий интеграл дифференциального уравнения.
Используя начальное условие, найдем произвольную постоянную С:
ln 1 + arctg 0 = C, откуда C = 0.
Найденную постоянную подставим в общий интеграл и отыщем частное решение:

Однородные дифференциальные уравнения
Определение. Функция двух переменных f (x, y) называется однородной n- го измерения, если выполняется условие
Например, f (x, y) = x 2 + y 2 , f (tx, ty) = t 2 f (x 2 + y 2 ) — однородная функция второго измерения.
Определение. Дифференциальное уравнение
y ‘= f (x, y) (7.10)
называется однородным, если функция f (x, y) однородная нулевого измерения.
Покажем, что это уравнение можно свести к уравнению с разделенными переменными.
Рассмотрим функцию f (tx, ty). Сделаем замену 

Тогда уравнение (7.10) запишется в виде 
В общем случае переменные в однородном уравнение не разделяются сразу. Но, если ввести вспомогательную неизвестную функцию u = u (x) по формуле

то мы сможем превратить однородное уравнение в уравнение с разделенными переменными.
Из формулы (7.12) найдем y’ = u + xu’ и уравнение 
то есть 

После интегрирования получим 
Отсюда находим выражение для функции u, возвращаемся к переменной y = xu и получим решение однородного уравнения.
Чаще всего не удается найти функцию u явно выраженной, тогда, после интегрирования, в левую часть следует подставить 
В результате получим решение уравнения в неявном виде.
Пример 1. Найти решение однородного уравнения
Решение. Заменой y = xu сведем заданное уравнение к уравнению


Отделяя переменные, найдем




Возвращаясь к переменной y, получим общее решение: 
Линейные дифференциальные уравнения
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение, которое содержит искомую функцию и ее производную в первой степени без их произведения:
y’ + P (x) y = Q (x). (7.13)
Здесь P (x), Q (x) — известные функции независимой переменной x. Например, y’ + 2 xy = x 2 .
Если Q (x) = 0, то уравнение (7.13) называется линейным однородным и является уравнением с разделяющимися переменными.
Если Q (x) ≠ 0, то уравнение (7.13) называется линейным неоднородным, которое можно решить несколькими способами.
Рассмотрим метод Бернулли, с помощью которого уравнение (7.13) можно свести к интегрированию двух дифференциальных уравнений первого порядка с разделяющимися переменными.
Решение дифференциального уравнения (7.13) ищем в виде y = u (x) v (x) или y = uv, (7.14)
где u (x), v (x) — неизвестные функции. Одну из этих функций можно взять произвольную, а другая определяется из уравнения (7.13).
Из равенства y = uv найдем производную y’:
y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение (7.13):
u’v + uv’ + P (x) ⋅ u⋅ v = Q (x) или u’v + u (v’ + P (x) ⋅ v) = Q (x).
Выберем функцию v такой, чтобы v’ + P (x) v = 0. (7.15)
Тогда для отыскания функции u получим уравнение:
u’v = Q (x). (7.16)
Сначала найдем v из уравнения (7.15).
Отделяя переменные, имеем 
Под неопределенным интегралом здесь будем понимать какую-то одну первообразную от функции P (x), то есть v будет определенной функцией от x.
Зная v, находим u из уравнения (7.16): 
откуда
Здесь мы уже берем для u все первообразные.
Найденные функции u и v подставляем в (7.14) и получаем общее решение линейного дифференциального уравнения:

При решении конкретных примеров проще выполнять эти выкладки, чем применять громоздкую формулу (7.17).
Пример 1. Решить дифференциальное уравнение 
Решение. Решение ищем в виде y = uv, тогда y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение: 

Выражение, стоящее в скобках, приравниваем к нулю, имеем

Отделим переменные, домножив обе части уравнения на 

После интегрирования, получим ln |v| = ln |x| (здесь ограничимся одной первообразной), откуда v = x.
Подставим v = x в уравнение (7.18):
Общее решение запишется:
y = x (x + C) = x 2 + Cx.
Пример 2. Найти частное решение дифференциального уравнения 
Решение. Заданное уравнение — это линейное неоднородное уравнение первого порядка, решение которого ищем в виде y = u⋅v.
Тогда 
Подставим v в уравнение и найдем u:
Общее решение дифференциального уравнения будет:
Подставляем начальные условия в найденное решение и находим С:
Из общего решения получаем частное решение 
Дифференциальное уравнение Бернулли
Определение. Уравнения вида


называется дифференциальным уравнением Бернулли.
Данное уравнение отличается от уравнения (7.13) только множителем y» (или x») в правой части. Для того, чтобы права часть данного уравнения была такой, как в (7.13), разделим его левую и праву часть на y»:
Сделаем замену: 
Домножим левую и правую части полученного уравнения на (n + 1) и, используя замену, получим: 
Мы получили линейное дифференциальное уравнение относительно новой переменной
Пример 1. Найти общее решение дифференциального уравнения xy’ + y = y 2 ln x.
Решение. 
Сделаем замену 
Данное уравнение решим, сделав замену z = u (x) ⋅ v (x).
Выбираем функцию v (x) так, чтобы выражение в скобках равнялось нулю, и эта функция была бы частным решением уравнения
Тогда 
Проинтегрировав правую часть этого уравнения по частям, получим 
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Обыновенное дефференциальное уравнение
Обыкновенным дифференциальным уравнением называется любое соотношение, связывающее независимую переменную 


Обыкновенное дифференциальное уравнение может быть приведено к виду
Здесь 
Число 
Обыкновенные дифференциальные уравнения первого порядка, разрешенные относительно производной. уравнения, интегрируемые в квадратурах
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Основные понятия и определения
Понятие об уравнении первого порядка, разрешенном относительно производной. В соответствии со сказанным во введении, уравнение первого порядка имеет вид
В этой главе мы будем рассматривать уравнение, разрешенное относительно производной:
Наряду с этим уравнением мы всегда будем рассматривать перевернутое уравнение
используя последнее в окрестности тех точек, в которых 
Во многих случаях оказывается целесообразным «место уравнении (2) и (2′) рассматривать одно равносильное им дифференциальное уравнение
Обе переменные 

Умножая обе части уравнения (3) на некоторую функцию 
где 


Иногда уравнение записывают *з так называемой симметрической форме:
Возможно вам будут полезны данные страницы:
Решение уравнения. Предположим, что правая часть уравнения (2), 




- Существует производная
для всех значений
из интервала
(Отсюда следует, что решение
представляет собою функцию, непрерывную ею всей области определения).
- Функция
обращает уравнение (2) в тождество:
справедливое для всех значений 





Так как наряду с уравнением (2) рассматривается перевернутое уравнение (2′), то и решения 
В этом смысле в дальнейшем мы будем для краткости называть решения уравнения (2′) решениями уравнения (2).
Примеры с решением
Пример 1.
является решением уравнения
в интервале 
справедливое при всех значениях
Пример 2.
Функция 

Пример 3.
является решением уравнения
в интервале
Иногда функцию 
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Системы обыкновенных дифференциальных уравнений
При решении многих задач нужно найти функции y1 = y1 (x), y2 = y2 (x), . yn = yn (x), которые удовлетворяют системе дифференциальных уравнений, содержащих независимую переменную x , искомые y1 , y2 , . yn и их производные.
Пример. Пусть материальная точка массы m имеет криволинейную траекторию движения в пространстве. Определить положение точки в любой момент времени t, когда на нее действует сила 
Положение точки в любой момент времени t определяется ее координатами x, y, z; следовательно, x, y, z являются функциями от t. Проекциями вектора скорости точки на оси координат будут производные x’ , y’ , z’.
Положим, что сила

функции определяются из уравнений динамики:
Мы получили систему трех дифференциальных уравнений второго порядка. В случае движения, когда траектория является плоской кривой, лежит, например, в плоскости Оxy, получим систему двух уравнений для определения неизвестных функций x (t) и y (t):
Рассмотрим простейшие системы дифференциальных уравнений.
Системы дифференциальных уравнений первого порядка
Система n уравнений первого порядка с n неизвестными функциями имеет вид:

где x — независимая переменная, y1, y2, . yn — неизвестные функции.
Если в левой части уравнений системы стоят производные первого порядка, а правые части уравнений вовсе не содержат производных, то такая система уравнений называется нормальной.
Решением системы называется совокупность функций y1, y2, . yn, которые превращают каждое уравнение системы в тождество относительно x.
Задача Коши для системы (7.38) состоит в нахождении функций y1, y2, . yn , удовлетворяющих систему (7.38) и заданные начальные условия:

Интегрирование системы (7.38) делают следующим образом. Дифференцируем по x первое уравнение системы (7.38): 
Заменим производные


Дифференцируем полученное уравнение и, подставив в это равенство значения производных из системы (7.38), найдем 
Продолжая дальше таким образом, получим 
В результате получаем следующую систему уравнений:

Из первых (n-1) уравнений определим y2, y3, . yn:

и подставим их значения в последнее уравнение системы (7.40) для определения y1:
Продифференцируем это выражение (n-1) раз, определим


Для того, чтобы полученное решение удовлетворяло заданным начальным условиям, остается только найти значение произвольных постоянных из уравнений (7.42) и (7.43) так, как мы это делали для одного дифференциального уравнения.
Пример 1. Проинтегрировать систему 
когда заданы начальные условия 
Решение. Дифференцируем по x первое уравнение, имеем: 



Из первого уравнения системы найдем 

Общим решением этого уравнения является

и тогда 
Подберем постоянные С1 и С2 так, чтобы выполнялись начальные условия. На основании (*) и (**) имеем:
1 = С1 – 9; 0 = С2 – 2С1 + 14, откуда С1 = 10, С2 = 6.
Таким образом, решением системы, которое удовлетворяет заданным начальным условиям, будет:
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Система дифференциальных уравнений:

где коэффициенты aij — постоянные числа, t — независимая переменная, x1 (t), . xn (t) —
неизвестные функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами.
Эту систему можно решать путем сведения к одному уравнению n-го порядка, как это было показано выше. Но эту систему можно решить и другим способом. Покажем, как это делается.
Будем искать решение системы (7.44) в виде:

Надо определить постоянные α1, α2, . αn и k так, чтобы функции (7.45) удовлетворяли систему (7.44). Подставим функции (7.45) в систему (7.44):
Сократим на e kt и преобразуем систему, сведя ее к такой системе:

Это система линейных алгебраических уравнений относительно α1, α2, . αn. Составим определитель системы:
Мы получим нетривиальные (ненулевые) решения (7.45) только при таких k, при которых определитель превратится в ноль. Получаем уравнение n-го порядка для определения k:
Это уравнение называется характеристическим уравнением для системы (7.44).
Рассмотрим отдельные случаи на примерах:
1) Корни характеристического уравнения действительны и различны. Решение системы записывается в виде:
Пример 2. Найти общее решение системы уравнений:
Решение. Составим характеристическое уравнение:

Решение системы ищем в виде
Составим систему (7.46) для корня k1 и найдем 


Откуда 


Итак, мы получили решение системы:
Далее составляем систему (7.46) для k = 4:
Откуда 
Получим второй решение системы: 
Общее решение системы будет:
2) Корни характеристического уравнения различны, но среди них есть комплексные:
k1 = α + iβ, k2 = α – iβ. Этим корням будут отвечать решения:


Можно доказать также, что истинные и мнимые части комплексного решения также будут решениями. Таким образом, получим два частных решения:

где 

Соответствующие комбинации функций (7.49) войдут в общий решение системы.
Пример 3. Найти общее решение системы
Решение. Составляем характеристическое уравнение:

Подставляем поочередно k1, k2 в систему (7.46), найдем
Запишем уравнение (7.47) и (7.48) для наших данных
Перепишем эти решения в таком виде:
За частные решения можно взять отдельно действительные и отдельно мнимые части:
Общим решением системы будет
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
📺 Видео
Дифференциальные уравнения с разделяющими переменными. 11 класс.Скачать

Однородное дифференциальное уравнениеСкачать

ЗАЧЕМ НУЖНЫ ЭТИ... производные! Математика на QWERTY.Скачать

Как распознать талантливого математикаСкачать

Математика это не ИсламСкачать

6. Особые решения ДУ первого порядкаСкачать

Метод Пикара последовательных приближений для решения дифференциальных уравненийСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Дифференциальные уравнения. 11 класс.Скачать

Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

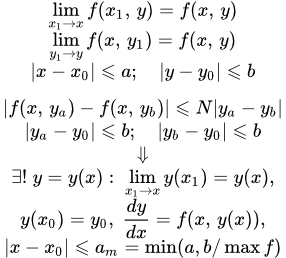


































 для всех значений
для всех значений  из интервала
из интервала  (Отсюда следует, что решение
(Отсюда следует, что решение  представляет собою функцию, непрерывную ею всей области определения).
представляет собою функцию, непрерывную ею всей области определения). обращает уравнение (2) в тождество:
обращает уравнение (2) в тождество: 


































