Про уравнения - легко » Статьи

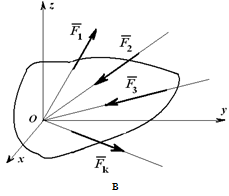
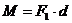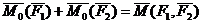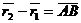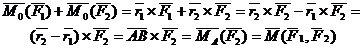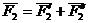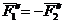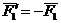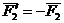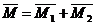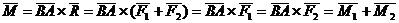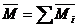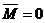Условия и уравнения равновесия системы пар

Обновлено
Содержание
  1. Условия равновесия пар сил.
  2. Условия равновесия пар сил
  3. Условия равновесия пар сил
  4. iSopromat.ru
  5. Формы условий равновесия
  6. Первая форма
  7. Вторая форма
  8. Третья форма
  9. Другие условия равновесия
  10. 🎥 Видео

Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

Статика. Условия равновесия плоской системы сил (23)

Условия равновесия пар сил.

Лекция 4

Краткое содержание: Пара сил. Теорема о сумме моментов пары сил. Теорема об эквивалентности пар сил. Теорема о переносе пары сил в параллельную плоскость. Теорема о сложении пар сил. Условия равновесия пар сил.

ПАРА СИЛ

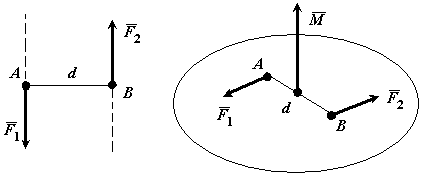
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Плоскостью действия пары сил называется плоскость в которой расположены эти силы.

Плечом пары сил d называется кратчайшее расстояние между линиями действия сил пары.

Моментом пары сил называется вектор 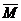Условия и уравнения равновесия системы пар, модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия сил пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки. Условия и уравнения равновесия системы пар

Условия и уравнения равновесия системы пар

Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.

Условия и уравнения равновесия системы пар

Доказательство: Выберем произвольно точку О. Проведем из нее в точки А и В радиус-векторы (Смотри Рис. 4.2).

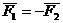
Условия и уравнения равновесия системы пар, Условия и уравнения равновесия системы пар

Условия и уравнения равновесия системы пар

Что и требовалось доказать.

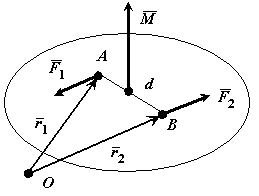Условия и уравнения равновесия системы пар

Рис. 4.2

Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.

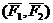
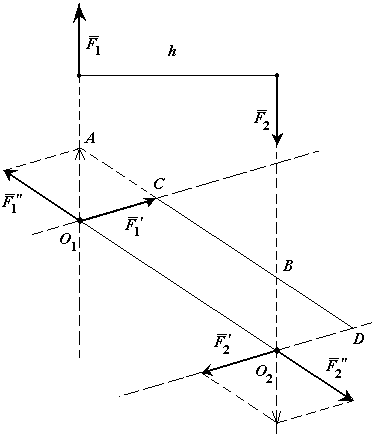
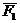
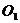
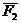
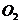
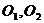
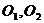
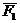
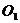
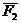
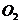
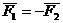
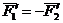
Доказательство: Пусть на твердое тело действует пара сил Условия и уравнения равновесия системы пар.

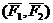
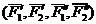
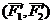
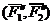
Условия и уравнения равновесия системы парПеренесем силу Условия и уравнения равновесия системы парв точку Условия и уравнения равновесия системы пар, а силу Условия и уравнения равновесия системы парв точку Условия и уравнения равновесия системы пар. Проведем через точки Условия и уравнения равновесия системы пардве любые параллельные прямые, пересекающие линии действия сил пары. Соединим точки Условия и уравнения равновесия системы паротрезком прямой и разложим силы Условия и уравнения равновесия системы парв точке Условия и уравнения равновесия системы пари Условия и уравнения равновесия системы парв точке Условия и уравнения равновесия системы парпо правилу параллелограмма.

Условия и уравнения равновесия системы пар

Условия и уравнения равновесия системы пар

Так как Условия и уравнения равновесия системы пар, то

Условия и уравнения равновесия системы пари Условия и уравнения равновесия системы пар

Поэтому Условия и уравнения равновесия системы парэквивалентна системе Условия и уравнения равновесия системы пар, а эта система эквивалентна системе Условия и уравнения равновесия системы пар, так как Условия и уравнения равновесия системы парэквивалентна нулю.

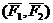
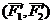
Таким образом мы заданную пару сил Условия и уравнения равновесия системы парзаменили другой парой сил Условия и уравнения равновесия системы пар. Докажем, что моменты у этих пар сил одинаковы.

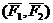
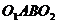
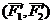
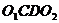
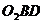
Момент исходной пары сил Условия и уравнения равновесия системы парчисленно равен площади параллелограмма Условия и уравнения равновесия системы пар, а момент пары сил Условия и уравнения равновесия системы парчисленно равен площади параллелограмма Условия и уравнения равновесия системы пар. Но площади этих параллелограммов равны, так как площадь треугольника Условия и уравнения равновесия системы парравна площади треугольника Условия и уравнения равновесия системы пар.

Что и требовалось доказать.

1. Пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия.

2. У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.

Теорема о переносе пары сил в параллельную плоскость.Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.

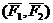
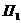
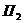
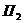
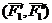
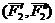
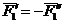
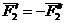
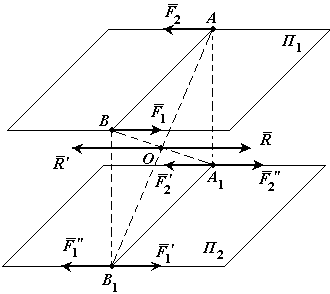
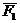
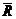
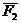
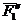
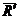
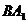
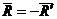
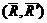
Доказательство: Пусть на твердое тело действует пара сил Условия и уравнения равновесия системы парв плоскости Условия и уравнения равновесия системы пар. Из точек приложения сил А и В опустим перпендикуляры на плоскость Условия и уравнения равновесия системы пари в точках их пересечения с плоскостью Условия и уравнения равновесия системы парприложим две системы сил Условия и уравнения равновесия системы пари Условия и уравнения равновесия системы пар, каждая из которых эквивалентна нулю.

Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы парУсловия и уравнения равновесия системы пар

Условия и уравнения равновесия системы парСложим две равные и параллельные силы Условия и уравнения равновесия системы пари Условия и уравнения равновесия системы пар. Их равнодействующая Условия и уравнения равновесия системы парпараллель-на этим силам, равна их сумме и приложена посредине отрезка Условия и уравнения равновесия системы парв точке О.

Сложим две равные и параллельные силы Условия и уравнения равновесия системы пари Условия и уравнения равновесия системы пар. Их равнодействующая Условия и уравнения равновесия системы парпараллель-на этим силам, равна их сумме и приложена посредине отрезка Условия и уравнения равновесия системы парв точке О.

Так как Условия и уравнения равновесия системы пар, то система сил Условия и уравнения равновесия системы парэквивалентна нулю и ее можно отбросить.

Таким образом пара сил 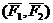Условия и уравнения равновесия системы парэквивалентна паре сил Условия и уравнения равновесия системы пар, но лежит в другой, параллельной плоскости. Что и требовалось доказать.

Следствие: Момент пары сил, действующий на твердое тело, есть свободный вектор.

Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению моменты.

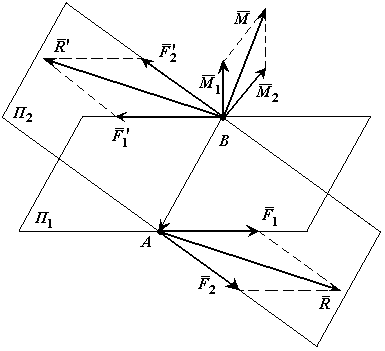Теорема о сложении пар сил.Две пары сил, действующих на одно и то же твердое тело, и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил. Условия и уравнения равновесия системы пар

Условия и уравнения равновесия системы пар

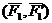
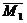
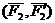
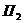
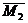
Доказательство: Пусть имеются две пары сил, расположенные в пересекающихся плоскостях. Пара сил Условия и уравнения равновесия системы парв плоскости Условия и уравнения равновесия системы пархарактеризуется моментом Условия и уравнения равновесия системы пар, а пара сил Условия и уравнения равновесия системы парв плоскости Условия и уравнения равновесия системы пархарактеризуется моментом Условия и уравнения равновесия системы пар.

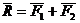
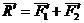
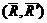
Расположим пары сил так, чтобы плечо пар было общим и располагалось на линии пересечения плоскостей. Складываем силы, приложенные в точке А и в точке В, Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар. Получаем пару сил Условия и уравнения равновесия системы пар.

Условия и уравнения равновесия системы пар

Что и требовалось доказать.

Условия равновесия пар сил.

Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

Условия и уравнения равновесия системы пар

Теорема.Для равновесия пар сил, приложенных к твердому телу, необхо-димо и достаточно, чтобы момент эквивалентной пары сил равнялся нулю.

Условия и уравнения равновесия системы пар

Теорема. Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций моментов пар сил на каждую из трех координатных осей была равна нулю.

Видео:Статика. Пара сил. Лекция (17)Скачать

Статика. Пара сил. Лекция (17)

Условия равновесия пар сил

Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар

Условия и уравнения равновесия системы пар

Видео:Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьников

Условия равновесия пар сил

  • Если пара сил действует так, как если бы она находилась в твердом пространстве, то пара этих сил должна быть равна паре сил, вектору. Что бы вы ни хотели, этот момент равен сумме векторных моментов данной пары сил, т. е. м = м. = 1. Векторный момент L7 геометрически рисуется замкнутым векторным многоугольником, построенным на векторном моменте заданной пары сил.

Общий метод, который мы используем, состоит в том, чтобы рассматривать тело как свободное и вводить вспомогательные неизвестные реакции, вызванные наложением связывания, называемые реакциями связывания. Людмила Фирмаль

Для равновесия пары сил, действующих на твердое тело, необходимо или достаточно, чтобы модуль векторного момента эквивалентной силы был равен нулю, или векторный многоугольник, построенный на основе векторного момента данной пары сил, замкнут. Итак, M = 0.И так оно и есть. L X = y Mix= 0 i 1 ф л, = 0 я = 1 М:= я Миз = 0.. = Я 10 Таким образом, для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций векторных моментов каждой пары сил по 3 координатным осям была равна нулю.

  • В общем случае 1 совокупность сил может быть уравновешена только 1 совокупностью сил, и никакая другая система сил, кроме 1 совокупности сил или 1 совокупности сил, не может быть уравновешена. Если пара сил действует на твердое тело в одной плоскости, то алгебраический момент может быть заменен 1 эквивалентной парой сил, равной сумме алгебраических моментов составляющих пар сил. М = ф м. я = 1. Для равновесия такой пары сил необходимо и достаточно, чтобы алгебраические моменты пар равных сил были равны нулю, то есть для равновесия пар сил, действующих на твердое тело в плоскости 1, сумма алгебраических моментов пар этих сил равна и достаточна нулю.

Таким образом, исследование первого приближения позволяет окончательно ответить на вопрос об устойчивости движения в том случае, когда корни характеристического уравнения имеют отрицательную или положительную вещественную часть. Людмила Фирмаль

Если на твердое тело воздействует только пара сил, расположенных в одной плоскости, то опорное противодействие должно уравновесить данную пару сил и составить эту пару сил. Например, если одна из 2 опор корпуса в точке B является роликовой опорой рис. 33, а другая неподвижным шарниром в точке A, то направление реакции в шарнире A противоположно направлению реакции в точке B. Реакции шарнирно подвижная опора в РБ Ролик расположен перпендикулярно плоскости опоры и вверх. Таким образом, Yal направлен параллельно RB. Величина этих реакций одинакова.

Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.

Условия и уравнения равновесия системы пар

Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар Условия и уравнения равновесия системы пар

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:§ 5.3. Уравнения равновесия плоской системы силСкачать

§ 5.3. Уравнения равновесия плоской системы сил

iSopromat.ru

Условия и уравнения равновесия системы пар

Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:

Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.

Если система уравновешена, то получаем условия равновесия: R=0, MO=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

Видео:Пара силСкачать

Пара сил

Формы условий равновесия

Первая форма

Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:

причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.

Вторая форма

Уравнения равновесия могут быть записаны иначе:

Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.

Третья форма

Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.

Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.

Видео:6. Приведение плоской системы сил к простейшему виду. Условия равновесияСкачать

6. Приведение плоской системы сил к простейшему виду. Условия равновесия

Другие условия равновесия

При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):

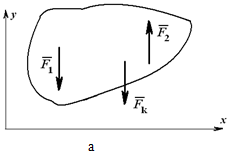
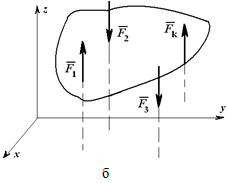
Условия и уравнения равновесия системы пар
Условия и уравнения равновесия системы пар
Условия и уравнения равновесия системы пар

Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:

Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:

и два уравнения для плоской системы:

В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

🎥 Видео

Уравновешивание системы пар силСкачать

Уравновешивание системы пар сил

Условия равновесия систем силСкачать

Условия равновесия систем сил

§ 5.2. Уравнения равновесия системы параллельных силСкачать

§ 5.2. Уравнения равновесия системы параллельных сил

§ 3.1. Пара сил и ее моментСкачать

§ 3.1. Пара сил и ее момент

Урок 187. Испарение и конденсация. Насыщенный пар и его свойстваСкачать

Урок 187. Испарение и конденсация. Насыщенный пар и его свойства

Урок 82. Равнодействующая параллельных сил. Пара силСкачать

Урок 82. Равнодействующая параллельных сил. Пара сил

Равновесие системы телСкачать

Равновесие системы тел

Основная теорема статикиСкачать

Основная теорема статики

Статика. Варианты условий равновесия. Лекция (22)Скачать

Статика. Варианты условий равновесия. Лекция (22)

Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.

Система сходящихся сил. Решение задач по МещерскомуСкачать

Система сходящихся сил. Решение задач по Мещерскому

Система сходящихся силСкачать

Система сходящихся сил

Статика. Условие равновесия. Лекция (21)Скачать

Статика. Условие равновесия. Лекция (21)

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1
Поделиться или сохранить к себе: