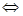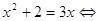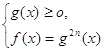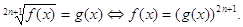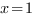Продолжаем изучать методы решения уравнений. Сейчас мы в деталях разберем метод возведения обеих частей уравнения в одну и ту же степень. Начнем с теории: рассмотрим, для решения каких уравнений применяется метод, опишем, в чем он состоит, приведем теоретическое обоснование метода возведения обеих частей уравнения в одну и ту же степень, запишем соответствующие алгоритмы решения уравнений. После этого сосредоточимся на практике и рассмотрим разнообразные примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень.
- Для решения каких уравнений применяется
- В чем состоит метод возведения обеих частей уравнения в одну и ту же степень
- Обоснование метода
- Алгоритмы решения уравнений методом возведения частей в одну и ту же степень
- Примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень
- Возведение обеих частей уравнения в квадрат
- Решение иррациональных уравнений
- 💡 Видео
Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Для решения каких уравнений применяется
Метод возведения обеих частей уравнения в одну и ту же степень в первую очередь применяется для решения иррациональных уравнений. Это объясняется тем, что возведение в натуральную и большую единицы степень позволяет избавляться от корней. Например, возведение в степень позволяет избавляться от корней при решении следующих уравнений:
, C≥0 , в частности,
,
и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению
, и дальше – к сравнительно простому уравнению без знаков корней x 2 −5=4 . Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению
и дальше — к элементарному уравнению 4−5·x=0 .
, например,
,
и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.
и
, таких как
,
и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень.
- уравнений с двумя, тремя корнями в записи, например,
и
. В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала.
- уравнений, в которых под знаком корня находятся другие корни, к примеру,
. Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.
- и это не весь список.
Метод возведения обеих частей уравнения в одну и ту же степень используется и для решения некоторых уравнений, в которых переменная находится в основаниях степеней с дробными показателями. Например, уравнение 
Также метод возведения частей уравнения в степень применяется при решении некоторых степенных уравнений, в которых фигурируют иррациональные показатели. В пример приведем два уравнения 



Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

В чем состоит метод возведения обеих частей уравнения в одну и ту же степень
Метод состоит в переходе к уравнению, которое получается из исходного путем возведения его обеих частей в одну и ту же степень, и нахождении решения исходного уравнения по решению полученного уравнения.
На практике наиболее часто прибегают к возведению обеих частей уравнения в одну и ту же натуральную степень, большую единицы, то есть, в квадрат, куб и т.д. Делается это на базе следующего утверждения:
Возведение обеих частей уравнения в одну и ту же четную натуральную степень дает уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечетную натуральную степень, большую единицы, дает равносильное уравнение (см. равносильные уравнения и уравнения-следствия).
Реже приходится обращаться к возведению обеих частей уравнения в другие степени, в частности, в дробные рациональные и иррациональные. В этих случаях отталкиваются от такого утверждения:
Уравнение A(x)=B(x) , на области допустимых значений переменной x для которого A(x)>0 или A(x)≥0 , B(x)>0 или B(x)≥0 , равносильно уравнению A r (x)=B r (x) , где r – положительное действительное число.
Видео:Иррациональное уравнение 634. Метод возведения обоих частей уравнения в одну и ту же степень.Скачать

Обоснование метода
Обоснованием метода возведения обеих частей уравнения в одну и ту же степень является доказательство утверждений из предыдущего пункта. Приведем эти доказательства.
Возведение обеих частей уравнения в одну и ту же четную натуральную степень дает уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечетную натуральную степень дает равносильное уравнение.
Докажем его для уравнений с одной переменной. Для уравнений с несколькими переменными принципы доказательства те же.
Пусть A(x)=B(x) – исходное уравнение и x0 – его корень. Так как x0 является корнем этого уравнения, то A(x0)=B(x0) – верное числовое равенство. Мы знаем такое свойство числовых равенств: почленное умножение верных числовых равенств дает верное числовое равенство. Умножим почленно 2·k , где k – натуральное число, верных числовых равенств A(x0)=B(x0) , это нам даст верное числовое равенство A 2·k (x0)=B 2·k (x0) . А полученное равенство означает, что x0 является корнем уравнения A 2·k (x)=B 2·k (x) , которое получено из исходного уравнения путем возведения его обеих частей в одну и ту же четную натуральную степень 2·k .
Для обоснования возможности существования корня уравнения A 2·k (x)=B 2·k (x) , который не является корнем исходного уравнения A(x)=B(x) , достаточно привести пример. Рассмотрим иррациональное уравнение 





Так доказано, что возведение обеих частей уравнения в одну и ту же четную натуральную степень приводит к уравнению-следствию.
Остается доказать, что возведение обеих частей уравнения в одну и ту же нечетную натуральную степень дает равносильное уравнение.
Покажем, что каждый корень уравнения является корнем уравнения, полученного из исходного путем возведения его обеих частей в нечетную степень, и обратно, что каждый корень уравнения, полученного из исходного путем возведения его обеих частей в нечетную степень, является корнем исходного уравнения.
Пусть перед нами уравнение A(x)=B(x) . Пусть x0 – его корень. Тогда является верным числовое равенство A(x0)=B(x0) . Изучая свойства верных числовых равенств, мы узнали, что верные числовые равенства можно почленно умножать. Почленно умножив 2·k+1 , где k – натуральное число, верных числовых равенств A(x0)=B(x0) получим верное числовое равенство A 2·k+1 (x0)=B 2·k+1 (x0) , которое означает, что x0 является корнем уравнения A 2·k+1 (x)=B 2·k+1 (x) . Теперь обратно. Пусть x0 – корень уравнения A 2·k+1 (x)=B 2·k+1 (x) . Значит числовое равенство A 2·k+1 (x0)=B 2·k+1 (x0) — верное. В силу существования корня нечетной степени из любого действительного числа и его единственности будет верным и равенство 

Так доказано, что возведение обеих частей иррационального уравнения в нечетную степень дает равносильное уравнение.
Доказанное утверждение пополняет известный нам арсенал, использующийся для решения уравнений, еще одним преобразованием уравнений – возведением обеих частей уравнения в одну и ту же натуральную степень. Возведение в одну и ту же четную степень обеих частей уравнения является преобразованием, приводящим к уравнению-следствию, а возведение в нечетную степень – равносильным преобразованием. На этом преобразовании базируется метод возведения обеих частей уравнения в одну и ту же степень.
Утверждение, касающееся возведения обеих частей уравнения в одну и ту же положительную действительную степень, доказывается аналогично с опорой на единственность степени положительного числа с действительным показателем.
Видео:Решение иррациональных уравнений методом возведения обеих частей в степень. ГВЭ11 + ЕГЭ 2021 #56Скачать

Алгоритмы решения уравнений методом возведения частей в одну и ту же степень
Есть смысл записать три алгоритма решения уравнений методом возведения обеих частей уравнения в одну и ту же степень: первый – для возведения в нечетную степень, второй – для возведения в четную степень, третий – для возведения в ненатуральную положительную степень.
Алгоритм решения уравнений методом возведения обеих частей в одну и ту же нечетную степень:
- Обе части уравнения возводятся в одну и ту же нечетную степень 2·k+1 .
- Решается полученное уравнение. Его решение есть решение исходного уравнения.
Алгоритм решения уравнений методом возведения обеих частей в одну и ту же четную степень:
- Обе части уравнения возводятся в одну и ту же четную степень 2·k .
- Решается полученное уравнение.
- Если полученное уравнение не имеет корней, то делается вывод об отсутствии корней у исходного уравнения.
- Если полученное уравнение имеет корни, то проводится отсеивание посторонних корней любым методом, не завязанным на области допустимых значений, например, через проверку подстановкой.
Обратите внимание: этот алгоритм, в отличие от предыдущего, содержит пункт, касающийся отсеивания посторонних корней. Это связано с тем, что возведение обеих частей уравнения в одну и ту же нечетную степень приводит к равносильному уравнению, а возведение обеих частей уравнения в четную степень в общем случае приводит к уравнению-следствию. Поэтому, в результате возведения в нечетную степень посторонние корни не возникают, а при возведении в четную степень посторонние корни могут появиться. Таким образом, при возведении частей уравнения в четную степень возникает необходимость в отсеивании посторонних корней. Почему отсеивание посторонних корней в этом случае нужно проводить методом, не использующим ОДЗ? Потому что возведение обеих частей уравнения в четную степень может приводить к появлению посторонних корней в пределах ОДЗ, и отсеять их по ОДЗ или по условиям ОДЗ невозможно.
Наконец, запишем алгоритм решения уравнений методом возведения обеих частей в одну и ту же положительную дробную рациональную или иррациональную степень:
- Убеждаемся, что выражения в левой и правой части уравнения не принимают отрицательных значений на ОДЗ для решаемого уравнения.
- Возводим обе части уравнения в одну и ту же положительную степень.
- Решаем полученное уравнение. Его решение дает искомое решение исходного уравнения.
Видео:Как решить уравнение - возведение в квадрат | Профильная МатематикаСкачать

Примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень
Большое количество попадающих под разбираемую тему примеров с подробными решениями приведено в статье решение иррациональных уравнений методом возведения обеих частей в одну и ту же степень. В добавление к этим примерам стоит разобрать решение уравнения через возведение обеих частей уравнения в одну и ту же степень, не являющуюся натуральным числом.
Решите уравнение
Решать заданное уравнение можно несколькими разными методами. Например, можно провести решение методом логарифмирования. Также можно преобразовать уравнение к виду 

Учитывая свойство степени в степени (см. свойства степеней), несложно догадаться, что избавиться от иррациональных показателей позволяет возведение обеих частей уравнения в степень 

Итак, проводим возведение обеих частей уравнения 


Решаем полученное уравнение:
Так мы пришли к кубическому уравнению x 3 −x 2 +2=0 . Один его корень x=−1 легко подбирается. Разделив многочлен x 3 −x 2 +2 на двучлен x+1 , получаем возможность представить кубическое уравнение в виде (x+1)·(x 2 −2·x+2)=0 . Квадратное уравнение x 2 −2·x+2=0 не имеет решений, так как его дискриминант отрицательный. Из этого заключаем, что уравнение x 3 −x 2 +2=0 имеет единственный корень x=−1 .
В процессе решения мы дважды отмечали, что нам будет необходимо сделать проверку найденных корней. Сейчас пришло это время. Проверку выполним через подстановку найденного корня x=−1 в исходное уравнение 
Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Возведение обеих частей уравнения в квадрат
2. Возведение обеих частей уравнения в квадрат.
Пусть даны два уравнения 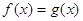
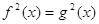
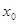
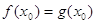
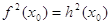
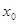
В то же время из равенства квадратов чисел не следует равенство этих чисел (числа могут быть противоположенными). Поэтому из уравнения (2) не следует уравнение (1). Отсюда вытекает, что если при решении уравнения использовалось возведение обеих частей уравнения в квадрат, то нужно повести дополнительное исследование, позволяющее исключить «посторонние» корни, если они появились.
Пример 1. Решить уравнение 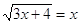
Решение. Возведем обе части этого уравнения в квадрат.
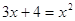
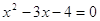
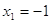
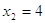
Если 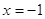
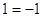
Если 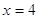
Следовательно, уравнение имеет единственный корень: 4.
3. Выполнение в одной части (или в обеих частях) уравнения тождественных преобразований, приводящих к расширению области определения равнения.
Если некоторое тождественное преобразование привело к расширению области определения уравнения, то получаем уравнения — следствие. При этом могут существовать такие значения переменной, которые являются корнями исходного уравнения.
Пример 1. Решить уравнение 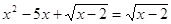
Решение. Выполнив приведение подобных слагаемых, получим: 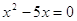
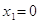
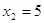
Если 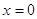
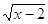
Если 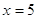
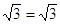
Следовательно, уравнение имеет единственный корень:5.
Пример 2. Решить уравнение 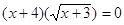
Решение. 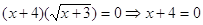
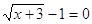
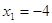
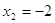
Если 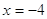
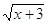
Если 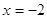
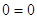
Следовательно, уравнение имеет единственный корень:-2.
Если при решении уравнения мы заменили его уравнением — следствием, то указанная выше проверка является неотъемлемой частью решения уравнения. Поэтому важно знать, при каких преобразованиях данное уравнение переходит в следствие.
Рассмотрим уравнение 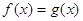
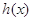
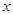
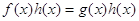
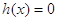
Значит, уравнение (4) есть следствие уравнения (3). Ясно, что уравнения (3) и (4) равносильны, если «постороннее» уравнение 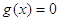
Теорема 1. Если обе части уравнения умножить на 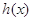
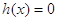
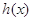
Пример 1. 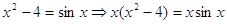
Заметим, что подобное преобразование, т.е. переход от уравнения (4) к уравнению (3) делением обеих частей уравнения (4) на выражение 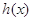
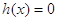
Пример 2. Уравнение 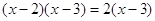
Деление обеих частей уравнения на 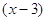
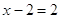
Снова возьмем уравнение (3) и возведем обе его части в квадрат. Получим уравнение: 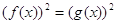
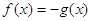
Пример 3. Уравнение 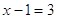
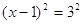
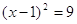
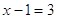
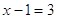
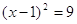
Теорема 2. При возведении обеих частей уравнения в квадрат (и вообще в любую четную степень) получается уравнение, являющееся следствием исходного.
Пример 1. 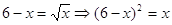
При решении иррационального уравнения чаще всего стараются заменить его более простым, но равносильным исходному. Поэтому важно знать равносильные преобразования.
Определение 10. Уравнение, имеющее одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными. Другими словами два уравнения называют равносильными, если множества их решений совпадают. Равносильность обозначается следующим образом: 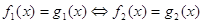
Пример 1. Уравнения 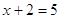
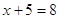
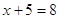
Пример 2. Уравнения 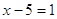
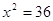
Пример 3. Уравнения 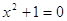
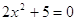
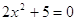
Определение 11. Пусть даны уравнения 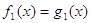
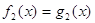
Пример 1. 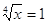
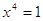
Отметим, что часто множество М совпадает либо с ОДЗ уравнения 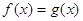
Имеется ряд теорем о равносильности уравнений.
Теорема 3. При возведении обеих частей уравнения в одну и ту же нечетную степень получается уравнение, равносильное исходному.
Пример 1. 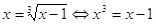
Теорема 4. Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное исходному.
Пример 1. 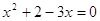
Теорема 5. Если обе части уравнения умножить или разделить на одно и тоже отличное от ноля число, то получится уравнение, равносильное исходному.
Пример 1. 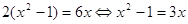
Теорема 6. Если в какой либо части уравнения выполнить тождественные преобразования, не меняющие области определения уравнения, то получится уравнение, равносильное исходному.
В школьной практике при решении иррациональных уравнений чаще всего используются два основных метода:
1) обеих частей уравнения в одну и ту же степень;
2) введение новых (вспомогательных) переменных.
Эти методы будем считать стандартными. В обязательном школьном курсе обычно этими методами и ограничиваются. Однако иногда приходится применять нестандартные методы и искусственные приемы решения иррациональных уравнений.
Типичная ошибка при решении иррациональных уравнений состоит в том, что школьники без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению «посторонних» корней.
При возведении обеих частей иррационального уравнения в одну и ту же степень надо иметь в виду, что если степень — не четное число, то получим равносильное уравнение, если же степень — четное число, то получим уравнение — следствие. Поэтому при решении иррациональных уравнений в большинстве случаев необходима проверка найденных решений.
Проверки можно избежать, если решать иррациональные уравнения с помощью равносильных замен. Для этого полезно знать следующие теоремы.
Теорема 7. Уравнение вида 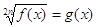
Уравнение вида
Теорема 8. Уравнение вида 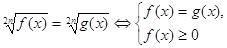
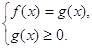
Уравнение вида 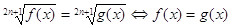
Далее рассмотрим более подробно типы иррациональных уравнений и методы их решения.
Видео:Возведение иррационального уравнения в квадратСкачать

Решение иррациональных уравнений

В этой статье мы поговорим о способах решения простейших иррациональных уравнений.
Иррациональным уравнением называется уравнение, которое содержит неизвестное под знаком корня.
Давайте рассмотрим два вида иррациональных уравнений, которые очень похожи на первый взгляд, но по сути сильно друг от друга отличаются.


В первом уравнении 
При возведении правой и левой части уравнения в нечетную степень мы можем не опасаться получить посторонние корни.
Пример 1 . Решим уравнение
Возведем обе части уравнения в третью степень. Получим равносильное уравнение:
Перенесем все слагаемые в одну сторону и вынесем за скобки х:
Приравняем каждый множитель к нулю, получим:


Посмотрим внимательно на второе уравнение: 


Чтобы решить уравнение такого вида, нужно обе части уравнения возвести в квадрат:

Возведение в квадрат может привести к появлению посторонних корней, поэтому нам надо учесть ОДЗ уравнения:


Однако, неравенство (4) следует из условия (3): если в правой части равенства стоит квадрат какого-то выражения, а квадрат любого выражения может принимать только неотрицательные значения, следовательно левая часть тоже должна быть неотрицательна. Поэтому условие (4) автоматически следует из условия (3) и наше уравнение 

Пример 2 . Решим уравнение:

Перейдем к равносильной системе:

Решим первое уравнение системы и проверим, какие корни удовлетворяют неравеству.

Неравеству 

Ответ: x=1
Внимание! Если мы в процессе решения возводим обе части уравнения в квадрат, то нужно помнить, что могут появиться посторонние корни. Поэтому либо нужно переходить к равносильной системе, либо в конце решения СДЕЛАТЬ ПРОВЕРКУ: найти корни и подставить их в исходное уравнение.
Пример 3 . Решим уравнение:
Чтобы решить это уравнение, нам также нужно возвести обе части в квадрат. Давайте в этом уравнении не будем заморачиваться с ОДЗ и условием существования корней, а просто в конце решения сделаем проверку.
Воозведем обе части уравнения в квадрат:
Перенесем слагаемое, содержащее корень влево, а все остальные слагаемые вправо:
Еще раз возведем обе части уравнения в квадрат:
По тереме Виета:

Сделаем проверку. Для этого подставим найденные корни в исходное уравнение. Очевидно, что при 
При 
Ответ:
💡 Видео
Подготовка к ЕГЭ #56. Решение иррациональных уравнений методом возведения обеих частей в степеньСкачать

Уравнения с корнем. Иррациональные уравнения #shortsСкачать

Решение иррациональных уравнений.Скачать

показательно степенное уравнение методом логарифмирования обеих частей уравненияСкачать

Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Сможешь решить иррациональное уравнение? Необычный метод решенияСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Понятие модуля | Возведение уравнения в квадратСкачать

Решение иррациональных уравнений 3Скачать

Возведение в квадратСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Иррациональные уравнения | Алгебра 8 класс #44 | ИнфоурокСкачать

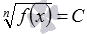 , C≥0 , в частности,
, C≥0 , в частности,  ,
,  и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению
и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению 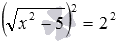 , и дальше – к сравнительно простому уравнению без знаков корней x 2 −5=4 . Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению
, и дальше – к сравнительно простому уравнению без знаков корней x 2 −5=4 . Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению 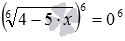 и дальше — к элементарному уравнению 4−5·x=0 .
и дальше — к элементарному уравнению 4−5·x=0 .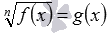 , например,
, например,  ,
,  и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.
и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.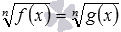 и
и  , таких как
, таких как 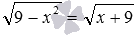 ,
, 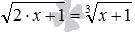 и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень.
и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень. и
и  . В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала.
. В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала. . Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.
. Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.