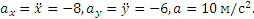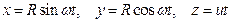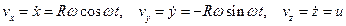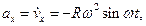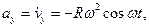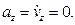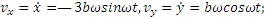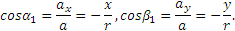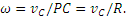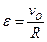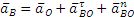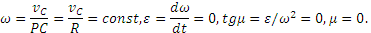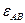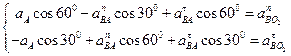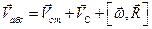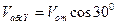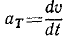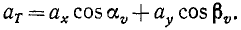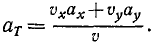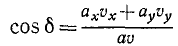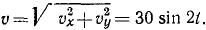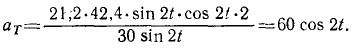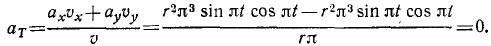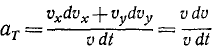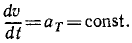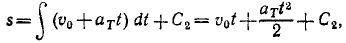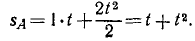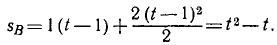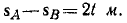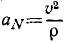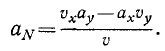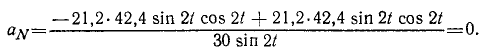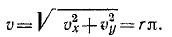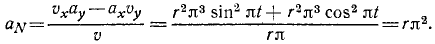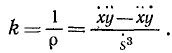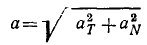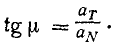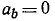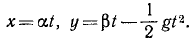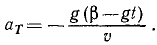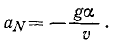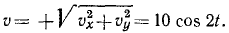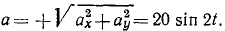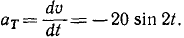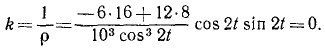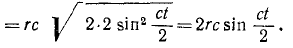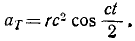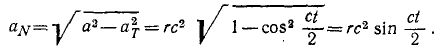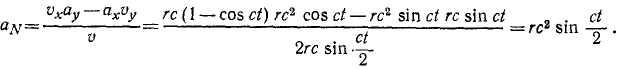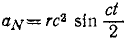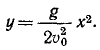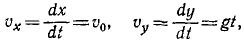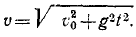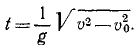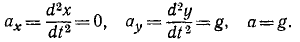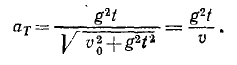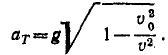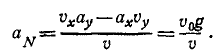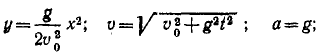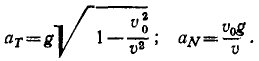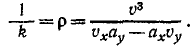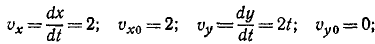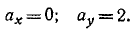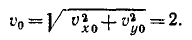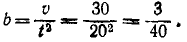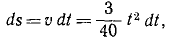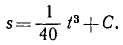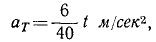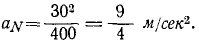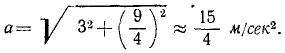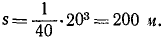Ускорение точки направлено если движение задано уравнениями х 2t у 2t (7 видео)

Примеры решения задач. Движение точки задано уравнениями (х, у — в метрах, t — в секундах).

Задача 2.1.

Движение точки задано уравнениями (х, у — в метрах, t — в секундах).

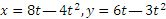
Определить траекторию, скорость и ускорение точки.

Решение.

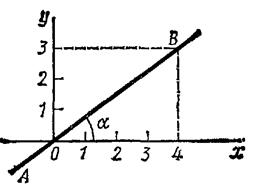Ускорение точки направлено если движение задано уравнениями х 2t у 2t

Рис. 2.9. К задаче 2.1

Для определения траектории исключаем из уравнений движения время t. Умножая обе части первого уравнения на 3, а обе части второго — на 4 и почленно вычитая из первого равенства второе, получим: или .

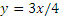
Следовательно, траектория — прямая линия, наклоненная к оси Ох под углом α, где 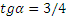(рис. 2.9).

Определяем скорость точки. По формулам (2.1) получаем:

;

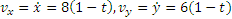
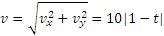
Теперь находим ускорение точки. Формулы (2.1) дают:

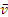
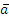
Направлены векторы и вдоль траектории, т. е. вдоль прямой АВ. Проекции ускорения на координатные оси все время отрицательны, следовательно, ускорение имеет постоянное направление от В к А. Проекции скорости при 0 1 с) обе проекции скорости отрицательны и, следовательно, скорость направлена от В к А, т. е. так же, как и ускорение.

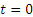
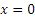
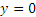
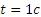
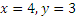
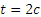
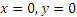
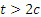
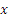
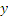
Заметим, наконец, что при и ; при (точка В); при ; при значения и растут по модулю, оставаясь отрицательными.

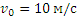
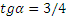
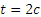
Итак, заданные в условиях задачи уравнения движения рассказывают нам всю историю движения точки. Движение начинается из точки О с начальной скоростью и происходит вдоль прямой АВ, наклоненной к оси Ох под углом α, для которого . На участке OB точка движется замедленно (модуль ее скорости убывает) и через одну секунду приходит в положение В (4, 3), где скорость ее обращается в нуль. Отсюда начинается ускоренное движение в обратную сторону. В момент точка вновь оказывается в начале координат и дальше продолжает свое движение вдоль ОА, Ускорение точки все время равно 10 м/с 2 .

Задача 2.2.

Движение точки задано уравнениями:

где 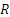, ω и u — постоянные величины. Определить траекторию, скорость и ускорение точки.

Решение.

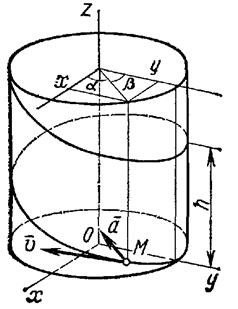Рис. 2.10. К задаче 2.2

Возводя первые два уравнения почленно в квадрат и складывая, получаем

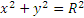
Следовательно, траектория лежит на круглом цилиндре радиуса R, ось которого направлена вдоль оси Oz (рис. 2.10). Определяя из последнего уравнения t и подставляя в первое, находим

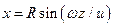
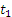
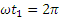
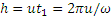
Таким образом, траекторией точки будет линия пересечения синусоидальной поверхности, образующие которой параллельны оси Оу (синусоидальный гофр) с цилиндрической поверхностью радиуса R. Эта кривая называется винтовой линией. Из уравнений движения видно, что один виток винтовой линий точка проходит за время , определяемое из равенства . При этом вдоль оси z точка за это время перемещается на величину , называемую шагом винтовой линии.

Найдем скорость и ускорение точки. Дифференцируя уравнения движения по времени, получаем:

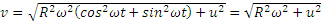
Стоящие под знаком радикала величины постоянны. Следовательно, движение происходит с постоянной по модулю скоростью, направленной по касательной к траектории. Теперь по формулам (2.1) вычисляем проекции ускорения;

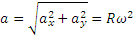
Итак, движение происходит с постоянным по модулю ускорением, Для определения направления ускорения имеем формулы:

’

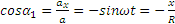
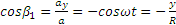
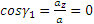
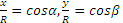
где α и β —углы, образуемые с осями Ох и Оу радиусом R, проведенным от оси цилиндра к движущейся точке. Так как косинусы углов α₁ и β₁ отличаются от косинусов α и β только знаками, то отсюда заключаем, что ускорение точки все время направлено по радиусу цилиндра к его оси.

Заметим, что хотя в данном случае движение и происходит со скоростью, постоянной по модулю, ускорение точки не равно нулю, так как направление скорости изменяется.

Задача 2.3.

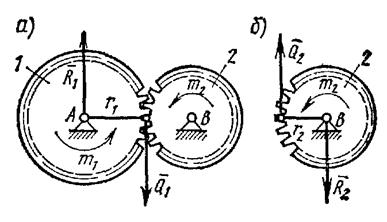
На шестерню 1 радиуса r₁ действует пара сил с моментом m₁ (рис. 46, а). Определить момент m₂ пары, которую надо приложить к шестерне 2 радиуса r₂, чтобы сохранить равновесие.

Решение.

Рис. 2.11. К задаче 2.3

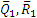
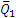
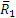
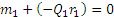
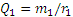
Рассмотрим сначала условия равновесия шестерни 1. На нее действует пара с моментом m₁, которая может быть уравновешена только действием другой пары, в данном случае пары . Здесь — перпендикулярная радиусу составляющая силы давления на зуб со стороны шестерни 2, a — тоже перпендикулярная радиусу составляющая реакции оси А (сила давления на зуб и реакция оси А имеют еще составляющие вдоль радиуса, которые взаимно уравновешиваются и в условие равновесия не войдут). При этом, согласно условию равновесия (17), и .

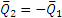
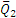
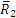
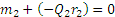
Теперь рассмотрим условия равновесия шестерни 2 (рис. 46, б). По закону равенства действия и противодействия на нее со стороны шестерни 1 будет действовать сила , которая с перпендикулярной радиусу составляющей реакции оси В образует пару , с моментом, равным -Q₂r₂. Эта пара и должна уравновеситься приложенной к шестерне 2 парой с моментом m₂; следовательно, по условию равновесия, . Отсюда, так как Q₂=Q₁ находим m₂=m₁/r₂r₁.

Естественно, что пары с моментами m₁ и m₂ не удовлетворяют условию равновесия , так как они приложены к разным телам.

Полученная в процессе решения задачи величина Q₁ (или Q₂) называется окружным усилием, действующим на шестерню. Как видим, окружное усилие равно моменту вращающей пары, деленному на радиус шестерни: Q₁=m₁/r₁ =m₂/r₂.

Задача 2.4.

Человек ростом h удаляется от фонаря, висящего на высоте H, двигаясь прямолинейно со скоростью 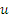. С какой скоростью движется конец тени человека?

Решение.

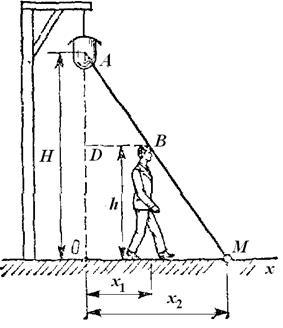Рис. 2.12. К задаче 2.4

Для решения задачи найдем сначала закон, по которому движется конец тени. Выбираем начало отсчета в точке О, находящейся на одной вертикали с фонарем, и направляем вдоль прямой, по которой движется конец тени, координатную ось Ох (рис. 2.12). Изображаем человека в произвольном положении на расстоянии x₁ от точки О. Тогда конец его тени будет находиться от начала О на расстоянии х₂.

Из подобия треугольников ОАМ и DAB находим:

Это уравнение выражает закон движения конца тени М, если закон движения человека, т.е. 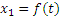, известен.

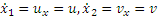
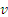
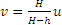
Взяв производную по времени от обеих частей равенства и замечая, что по формуле (2.1) , где — искомая скорость, получим

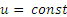
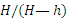
Если человек движется с постоянной скоростью ( ), то скорость конца тени М будет тоже постоянна, но в раз больше, чем скорость человека.

Обращаем внимание на то, что при составлении уравнений движения надо изображать движущееся тело или механизм в произвольном положении. Только тогда мы поучим уравнения, определяющие положение движущейся точки (или тела) в любой момент времени.

Задача 2.5.

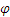
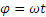
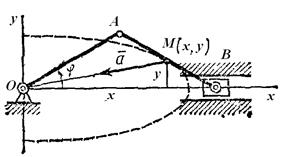Определить траекторию, скорость и ускорение середины М шатуна кривошипно-ползунного механизма (рис. 2.13), если OA=AB=2b, а угол при вращении кривошипа растет пропорционально времени: .

Рис. 2.13. К задаче 2.5.

Начинаем с определения уравнений движения точки М. Проводя оси и обозначая координаты точки М в произвольном положении через х и у находим

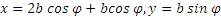
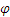
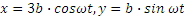
Заменяя его значением, получаем уравнения движения точки М:

Для определения траектории точки М представим уравнения движения в виде

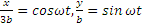
Возводя эти равенства почленно в квадрат и складывая, получим

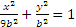
Итак, траектория точки М — эллипс с полуосями 3b и b.

Теперь по формуле (2.1) находим скорость точки М:

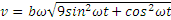
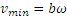
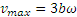
Скорость оказывается величиной переменной, меняющейся с течением времени в пределах от до .

Далее по формулам (2.1) определяем проекции ускорения точки М;

;

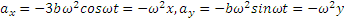
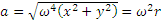
где 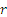— длина радиуса-вектора, проведанного из центра О до точки М. Следовательно, модуль ускорения точки меняется пропорционально ее расстояние от центра эллипса.

Определелим направление ускорения

Отсюда находим, что ускорение точки М все время направлено вдоль МО к центру эллипса.

Задача 2.6.

Вал, делающий n=90 об/мин, после выключения двигателя начинает вращаться равнозамедленно и останавливается через t₁=40 с. Определить, сколько оборотов сделал вал за это время.

Решение.

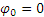
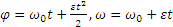
Так как вал вращается равнозамедленно, то для него, считая , будет

. (2.2)

Начальной угловой скоростью при замедленном вращении является та, которую вал имел до выключения двигателя. Следовательно,

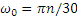
В момент остановки при t=t₁ угловая скорость вала ω₁=0. Подставляя эти значения во второе из уравнений (2.2), получаем:

и .

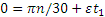
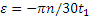
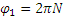
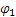
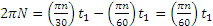
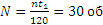
Если обозначить число сделанных валом за время t₁ оборотов через N (не смешивать с n; n — угловая скорость), то угол поворота за то же время будет равен . Подставляя найденные значения ε и в первое из уравнений (а), получим

Задача 2.7.

Маховик радиусом R=0,6 м вращается равномерно, делая n=90 об/мин. Определить скорость и ускорение точки, лежащей на ободе маховика.

Решение.

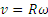
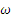
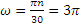
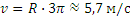
Скорость точки обода , где угловая скорость должна быть выражена в радианах в секунду. Тогда и .

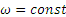
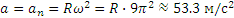
Далее, так как , то ε=0, и, следовательно,

Ускорение точки направлено в данном случае к оси вращения.

Задача 2.8.

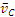
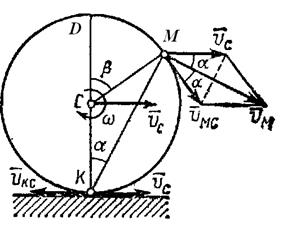Найти скорость точки М обода колеса, катящегося по прямолинейному рельсу без скольжения (рис. 2.14), если скорость центра С колеса равна , а угол DKM=α.

Рис. 2.14. К задаче 2.8.

Решение

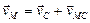
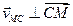
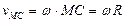
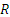
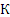
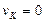
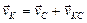
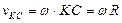
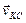
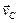
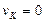
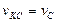
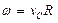
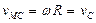
Приняв точку С, скорость которой известна, за полюс, найдем, что , где по модулю ( — радиус колеса). Значение угловой скорости со найдем из условия того, что точка колеса не скользит по рельсу и, следовательно, в данный момент времени . С другой стороны, так же как и для точки М, где . Так как для точки К скорости и направлены вдоль одной прямой, то при , откуда . В результате находим, что .

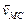
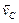
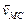
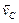
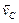
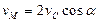
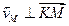
Параллелограмм, построенный на векторах и , будет при этом ромбом. Угол между и равен β, так как стороны, образующие этот угол и угол β, взаимно перпендикулярны. В свою очередь угол β=2α, как центральный угол, опирающийся на ту же дугу, что и вписанный угол α. Тогда по свойствам ромба углы между и и между и тоже равны α. Окончательно, так как диагонали ромба взаимно перпендикулярны, получим

и .

Задача 2.9.

Определить скорость точки М обода катящегося колеса, рассмотренного в предыдущей задаче, с помощью мгновенного центра скоростей.

Решение.

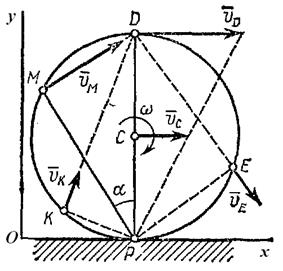Рис. 2.15. К задаче 2.9.

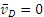
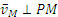
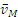
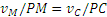
Точка касания колеса Р (рис. 2.15) является мгновенным центром скоростей, поскольку . Следовательно, . Так как прямой угол PMD опирается на диаметр, то направление вектора скорости любой точки обода проходит через точку D. Составляя пропорцию и замечая,

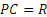
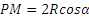
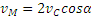
что , a , находим .

Чем точка М дальше от Р, тем ее скорость больше; наибольшую скорость 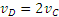имеет верхний конец D вертикального диаметра. Угловая скорость колеса имеет значение

Аналогичная картина распределения скоростей имеет место при качении колеса или шестерни по любой цилиндрической поверхности.

Задача 2.10.

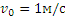
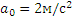
Центр О колеса, катящегося по прямолинейному рельсу (рис. 2.16), имеет в данный момент времени скорость и ускорение . Радиус колеса R=0,2 м. Определить ускорение точки В — конца перпендикулярного ОР диаметра АВ и ускорение точки Р, совпадающей с мгновенным центром скоростей.

Решение.

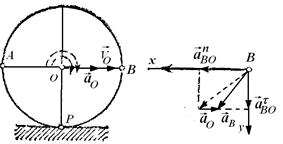Рис. 2.16. К задаче 2.10.

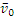
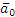
1) Так как и известны, принимаем точку О за полюс.

2) Определение ω. Точка касания Р является мгновенным центром скоростей; следовательно, угловая скорость колеса

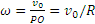
3) Определение ε. Так как величина PO=R остается постоянной при любом положении колеса, то

Знаки ω и ε совпадают, следовательно, вращение колеса ускоренное.

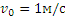
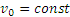
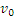
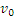
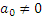
а) не следует думать, что если по условиям задачи , то . Значение в задаче указано для данного момента времени; с течением же времени изменяется, так как ;

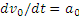
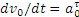
б) в данном случае , так как движение точки O является прямолинейным. В общем случае .

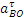
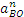
4) Определение и . Так как за полюс взята точка O, то ускорение точки B определяется по фомуле:

Учитывая, что в нашем случае BO=R, находим:

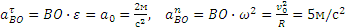
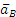
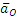
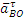
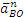
Показав на чертеже точку B отдельно, изображаем (без соблюдения масштаба) векторы, из которых слагается ускорение , а именно: вектор (переносим из точки O), вектор (в сторону вращения, так как оно ускоренное) и вектор (всегда от B к полюсу O).

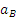
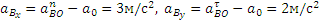
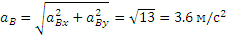
5) Вычисление . Проведя оси X и Y, находим, что

Аналогичным путем легко найти и ускорение точки P: 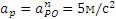и направлено вдоль PO. Таким образом, ускорение точки P, скорость которой в данный момент времени равна нулю, нулю не равно.

Задача 2.11.

Колесо катится по прямолинейному рельсу так, что скорость 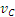его центра С постоянна. Определить ускорение точки М обода колеса (рис. 2.17).

Решение.

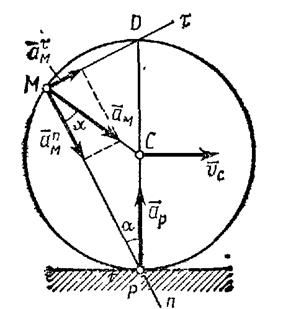Рис. 2.17. К задаче 2.11.

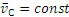
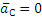
Так как по условиям задачи , то и точка С является мгновенным центром ускорений. Мгновенный центр скоростей находится в точке Р. Следовательно, для колеса

В результате ускорение точки М

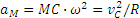
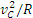
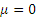
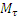
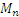
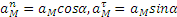
Таким образом, ускорение любой точки М обода (в том числе и точки Р) равно и направлено к центру С колеса, так как угол . Заметим, что это ускорение для точки М не будет нормальным ускорением. В самом деле, скорость точки М направлена перпендикулярно РМ . Следовательно, касательная к траектории точки М направлена вдоль линии MD, а главная нормаль — вдоль МР. Поэтому

Зажача 2.12.

Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна С, соединенных друг с другом и с неподвижными опорами О₁ и О₂ шарнирами (рис.2.17 а). Точка D находится в середине стержня АВ. Длины стержней равны соответственно L₁=0,4 м, L₂ =1,2 м, L₃=1,4 м, L₄=0,6 м.

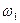
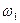
Дано: = 6 с -1 , величина постоянная. Заданную угловую скорость считать направленной против часовой стрелки.

Найти: скорости точек В и C; угловую скорость 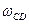; ускорение точки В; угловое ускорение

а)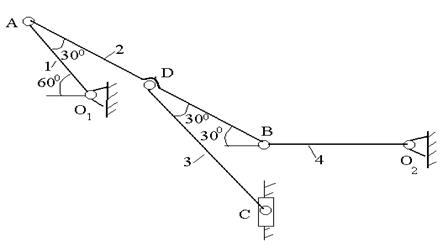
б)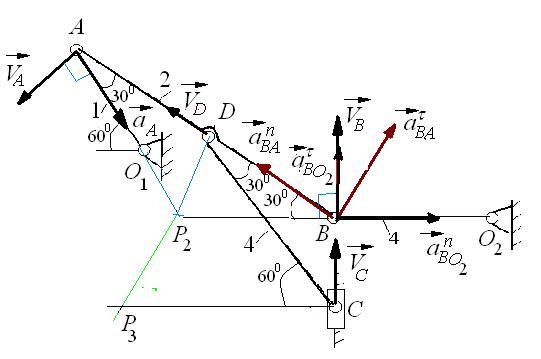
Рис.2.17. К задаче 2.12.

Решение (рис.2.12б)

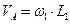
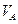
1. Определим скорость точки А. Стержень OAвращается вокруг точко O₁, поэтому скорость точки А определяется по формуле = 1,6 м/с и направлена перпендикулярно отрезку O₁А. = 1,6 м/с

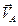
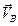
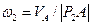
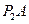
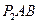
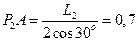
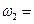
2. Определим угловую скорость стержня АВ. Точка В вращается вокруг центра О₂, поэтому ее скорость перпендикулярна отрезку O₂B. Для нахождения мгновенного центра скоростей отрезка АВ в точках А и В восстановим перпендикуляры к векторам и . Точка пересечения этих перпендикуляров Р₂ является мгновенным центром скоростей второго стержня. Угловая скорость вычисляется по формуле . Расстояние определяется из равнобедренного треугольника , то есть м. Поэтому 2,3 с -1 .

3. Определим скорость точки В по формуле 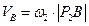= 1,6 м/с

по формуле 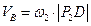= 0,8 м/с

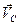
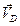
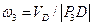
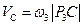
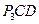
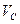
4. Определим скорость точки С. Так как точка С движется прямолинейно, то ее скорость направлена вдоль движения ползуна. Для нахождения мгновенного центра скоростей отрезка CD в точках C и D восстановим перпендикуляры к векторам и . Точка пересечения этих перпендикуляров Р₃ является мгновенным центром скоростей третьего стержня. Угловая скорость вычисляется по формуле , а скорость точки С . Так как треугольник равносторонний, то = 0,8 м/с

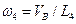
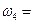
5. Определим угловую скорость отрезка О₂В. Известно, что центром скоростей этого стержня является точка О₂В , а также скорость точки B. Поэтому угловая скорость четвертого стержня вычисляется по формуле и 2,7 с -1 .

6. Определим ускорение точки А. Так как первый стержень вращается равномерно, то точка А имеет относительно О₁ только нормальное ускорение, которое вычисляется по формуле 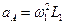= 6,4 м/с 2 .

7. Определим ускорение точки В, которая принадлежит двум стержням — АВ и О₂В. Поэтому ускорение точки В определяется с помощью двух формул

и , где

— ускорение точки А;

— нормальное ускорение точки В относительно А;

— тангенциальное ускорение точки В относительно А;

— нормальное ускорение точки В относительно О₂;

— тангенциальное ускорение точки В относительно О₂.

= 6,4 м/с 2 ; = 4,3 м/с 2 .

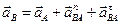
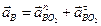
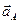
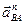
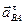
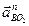
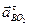
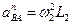
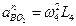
Можно составить уравнение

, которое в проекциях на оси координат имеет вид

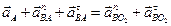
Решив полученную систему двух уравнений с двумя неизвестными, получим:

= 13,2 м/с 2 , а_ВХ = 4,1 м/с 2 , а_В_Y =9,1 м/с 2 , а_В =10 м/с 2 .

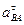
8. Определим угловое ускорение стержня АВ, используя формулу 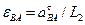= 13,2 с -2 .

Задача 2.13.

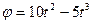
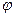
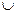
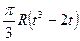
Круглая пластина радиуса R=60 см вращается вокруг неподвижной оси по закону (рис.2.18 а). Положительное направление угла показано на рисунке дуговой стрелкой. Ось вращения ОО₁ лежит в плоскости пластины (пластина вращается в пространстве). По окружности радиуса R движется точка М. Закон ее движения по дуге окружности s= АМ= . На рисунке точка М показана в положении, когда s положительно, при s отрицательном точка М находится по другую сторону от точки А; L=R.

Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t=1 с.

а)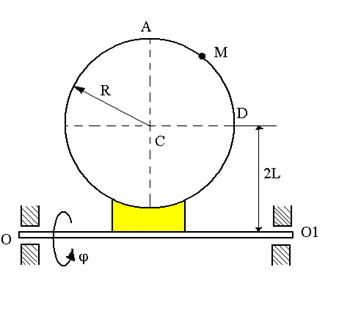
б)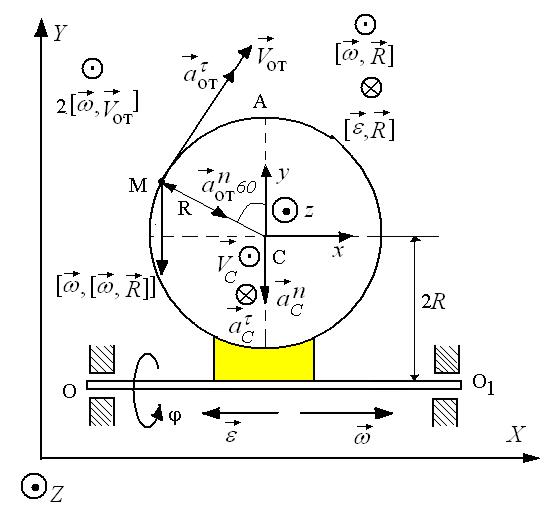
Рис.2.18. К задаче 2.13.

Решение (рис.2.13 б)

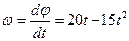
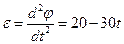
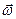
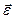
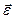
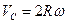
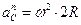
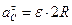
В качестве подвижной системы координат xyz примем точку С. Эта система совершает вращательное движение с угловой скоростью = 5 с -1 . Угловое ускорение = -10 с -2 . Направления векторов и опледеляются по правилу буравчика и изображены на рис. Причем, вектор направлен в противоположную сторону, так как его значение его проекции на ось OХ неподвижной системы координат XYZ отрицательно. Вычислим скорость и ускорение центра подвижной системы координат С, которая движется по окружности. Скорость вычисляется по формуле , равна 600 см/с и первендикулярна плоскости рисунка. Ускорение точки С состоит из двух компонент — нормальное = 3000 см/с 2 и тангенциальное = 1200 см/с 2 ускорения.

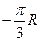
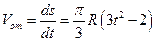
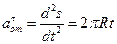
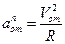
Вычислим путь, относительную скорость и ускорение точки M. Ее положение определяется величиной дуги S, в данный момент времени S = , поэтому она располагается слева от точки А. Относительная скорость . В данный момент времени она равна 63 см/с и направлена по касательной к окружности. Относительное ускорение является суммой двух составляющих — тангенциальное = 377 см/с -2 и нормальное = 66 см/с -2 .

Абсолютная скорость точки M определяется по формуле

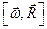
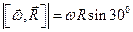
Где — переносная скорость вращательного движения, модуль которой = 150 см / с, ее направление определяется по правилу Жуковского. В разложении на оси координат

По теореме Пифагора 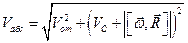= 750 м /с.

Абсолютное ускорение точки M определяется по формуле

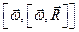
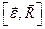
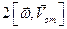
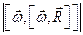
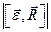
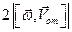
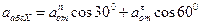
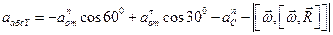
Где и — соответственно нормальное и тангенциальное переносные ускорения вращательного движения, — кориолисово ускорение.

= 750 м / с -2 ; =300 м / с -2 ; = 546 м / с -2

;

Содержание

Заданы уравнения движения точки x=3t, y=t2. Определите скорость точки в момент времени t = 2c.
Касательное и нормальное ускорения точки в теоретической механике
Касательное и нормальное ускорения точки
Проекция ускорения на касательную и на нормаль
Касательное ускорение
Равнопеременное движение точки
Нормальное ускорение
Ускорение при естественном способе задания движения
🔍 Видео

Видео:К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Заданы уравнения движения точки x=3t, y=t2. Определите скорость точки в момент времени t = 2c.

X=3t, Y=t в квадрате, берем производные, получим
Vx=3, Vy=2t
Скорость равна V= квадратный корень из (Vx в квадрате+Vy в квадрате) = квадратный корень из (9+16)= 5.

Как это сложно. Здесь без академика не обойтись

x= 3*2c.
y= 2*2c.
x= 6
y= 4
как сложно 1 класс

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Касательное и нормальное ускорения точки в теоретической механике

Касательное и нормальное ускорения точки

Касательное ускорение характеризует изменение в данное мгновение вектора скорости по величине, а нормальное — по направлению

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Проекция ускорения на касательную и на нормаль

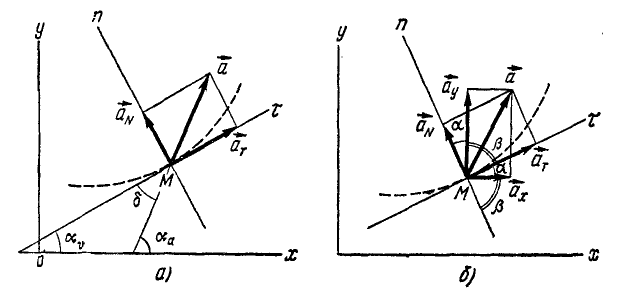
Если движение точки задано в векторной или в координатной форме, то часто встречается необходимость определить проекции ускорения на касательную и главную нормаль к траектории точки в том ‘ месте, где в данное мгновение находится точка (рис. 91, а).

При естественной форме определения движения точки сначала определяют проекции ускорения на касательную и на нормаль, а затем уже по этим проекциям находят величину и направление полного ускорения точки.

Проекцию ускорения точки на касательную к ее траектории называют касательным ускорением, или тангенциальным ускорением (от латинского слова tangens—касающийся), и обозначают a_N.

Проекцию ускорения на нормаль называют нормальным ускорением и обозначают a_r.
Часто касательное и нормальное ускорения рассматривают не как проекции, а как составляющие полного ускорения, т. е. как векторные величины. В таком случае над а_r и a_N ставят стрелку, указывающую на их векторный характер.

Разложение ускорения по касательной и нормали имеет физический смысл: касательная составляющая ускорения направлена по касательной (как и скорость), а потому не может повлиять на направление скорости, но влияет на ее величину; составляющая ускорения по нормали направлена перпендикулярно к скорости, а потому не может повлиять на величину скорости, но влияет на ее направление.

Касательное ускорение равно первой производной от величины скорости по времени:

Видео:Кинематика точки. Авторы: Борисов Никита, Ларионов Егор, Петрашова Полина. Решение задачи.Скачать

Касательное ускорение

Пусть точка M движется по траектории, расположенной в плоскости хОу.
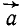
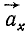
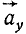
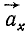
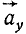
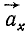
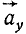
Проведем касательную и нормаль к кривой в точке M (рис. 91, б), нанесем на чертеж вектор ускорения точки M и его составляющие и по координатным осям. Чтобы определить касательное ускорение, надо спроецировать на касательную вектор полного ускорения или найти алгебраическую сумму проекций на касательную составляющих и полного ускорения по осям координат. Воспользовавшись вторым из этих способов, спроецируем и на касательную:

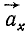
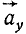
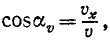
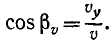
Составляющие ускорения и направлены по координатным осям, а направление касательной совпадает с направлением скорости, поэтому косинусы углов а и β равны направляющим косинусам скорости:

(62′)

(62»)

Подставляя значения направляющих косинусов, получаем

По формуле (68) удобно вычислять касательное ускорение точки, если ее движение задано в координатной форме уравнениями (58′) и (58″).

Можно дать еще другой изящный вывод формулы (68) тангенциального ускорения, для чего спроецировать на касательную вектор полного ускорения, не раскладывая его предварительно по осям декартовых координат. В самом деле, тангенциальное ускорение равно проекции полного ускорения на касательную (рис. 91, а):

a_r = a cos δ,
но угол δ, как внутренний угол треугольника, равен внешнему α_а без другого внутреннего α_υ, поэтому:

Подставляя сюда вместо направляющих косинусов их выражения (67) n (62′), получим

Напомним, что в числителе этой формулы проекции имеют свой знак, а знаменатель определяется по (64), т. е. существенно положителен.

Задача №1

Движение точки задано в декартовых координатах уравнениями:

x=21,2 sin 2 t, y=21,2 cos 2 t

Определить касательное ускорение точки (см. задачу № 36, стр. 132).

Решение. Дифференцируя уравнения движения, найдем υ_x = 21,2 sin 2t, υ_y = -21,2 sin 2t. Определим теперь полную скорость:

Дифференцируя уравнения движения вторично, найдем

Касательное ускорение определим по формуле (68):

Ответ. Касательное ускорение равно 60 cos 2t.

Задача №2

Точка M движется в системе координат хОу согласно уравнениям x=r cos πt, y=r sin πt. Найти касательное ускорение точки М.

Решение. Проекции скорости и ускорения на оси координат, а также и полная скорость точки M были уже нами получены при решении задачи № 44 (см. стр. 142). Для определения касательного ускорения точки M нам остается только подставить эти величины в формулу (68):

Ответ. Касательное ускорение равняется нулю.

Для случая задания движения в естественной форме преобразуем формулу (68) следующим образом:

и, сокращая на υ, найдем касательное ускорение

(69)

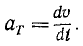
Принимая во внимание (53), можно придать этой формуле несколько иной вид:

(69′)

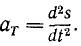
Итак, касательное ускорение—это проекция ускорения точки на касательную к траектории, равная первой производной от величины скорости по времени. Чтобы получить касательное ускорение в векторном выражении, нужно его умножить на единичный вектор касательной:

(69»)

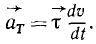
Как уже было сказано, касательное ускорение не может изменить направления скорости, оно характеризует быстроту изменения величины скорости, т. е. соответствует изменению вектора скорости вдоль его направления.

Если с течением времени величина скорости увеличивается, то касательное ускорение направлено в ту же сторону, что и скорость. Такое движение называют ускоренным.

Если же величина скорости уменьшается, то касательное ускорение направлено в сторону, противоположную скорости. Такое движение называют замедленным.

Каждое из этих движений называют переменным движением.

Если величина скорости точки постоянна, то производная 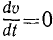, а потому равно нулю и касательное ускорение. Движение точки с постоянной по величине скоростью по любой траектории называют равномерным. Следовательно, при равномерном движении точки касательное ускорение равно нулю.

Обратное заключение можно сделать лишь с некоторой оговоркой: если касательное ускорение постоянно равняется нулю, то, следовательно, величина скорости постоянна и движение равномерно; если же касательное ускорение точки равняется нулю не в течение всего рассматриваемого промежутка времени, а только в какое-то мгновение, то движение точки не является равномерным, и равенство 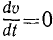означает, что в это мгновение величина скорости достигла экстремального (максимального или минимального) значения.

При равномерном движении точки по любой траектории

(70)

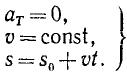
Формулы (70) справедливы только для равномерного движения точки и неприменимы при других движениях.

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Равнопеременное движение точки

Из переменных движений точки в задачах наиболее часто встречается равнопеременное движение — такое движение, при котором касательное ускорение остается постоянным.

При равнопеременном движении точки по любой траектории
(71)

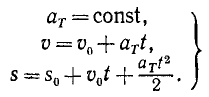
Формулы (71) справедливы только для равнопеременного движения и неприменимы при других движениях. Они даны здесь без вывода и известны из элементарной физики. Вывод этих формул приведен в решении задачи № 48.

Задача №3

Точка А начала двигаться с начальной скоростью υ₀= 1 м/сек и с ускорением a_T =2 м/сек 2 . Через одну секунду следом за точкой А по той же траектории с такой же начальной скоростью и с таким же касательным ускорением стала двигаться точка В. Определить расстояние (по траектории) между точками А и В через t сек после выхода первой точки. Построить графики движения точек.

Решение. Определим сначала уравнение движения точек. Нам дано, что

Разделяя переменные и интегрируя, получим

Постоянную C₁ определим из начальных данных:

Написав υ по (53), разделяя переменные и интегрируя, найдем

Подставляя вместо υ₀ и а_T заданные величины, найдем расстояние (в м), пройденное точкой А за время t:

В то же мгновение t расстояние, пройденное точкой В, будет меньше, так как точка В будет находиться в пути лишь t—1 сек. Для точки В

Расстояние между A и B найдем как разность пройденных ими путей:

Это расстояние растет пропорционально времени, хотя точка В во времени не отстает от точки А и каждую точку траектории проходит через 1 сек после того, как через нее прошла точка А.

Графики движения точек А и В изображаются одинаковыми параболами (рис. 92), но парабола, представляющая движение точки В, смещена по оси времени относительно параболы, представляющей движение точки А, на 1 сек вправо. Чтобы определить расстояние (в м) между А и В в какое-либо мгновение, надо восставить перпендикуляр к оси времени в точке, соответствующей этому мгновению, и измерить расстояние по вертикали между параболами. Чтобы определить интервал времени (в сек) между прохождениями точками А и В какой-либо точки К траектории, надо восставить перпендикуляр к оси расстояний в точке, соответствующей расстоянию точки К от начала отсчета, и измерить расстояние по горизонтали между параболами. Графики наглядно показывают, что точка В отстает от точки А по расстоянию, так как А В непрерывно увеличивается, но не отстает по времени, и точка В проходит каждый отрезок траектории за такое же время, как и точка А.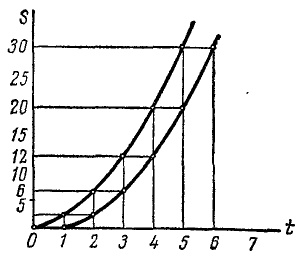

Рис. 92

Нормальное ускорение равно отношению квадрата скорости точки к радиусу кривизны траектории:

Видео:Сложное движение точки (скорость и ускорение муфты)Скачать

Нормальное ускорение

Чтобы получить формулы нормального ускорения, мы опять воспользуемся тем, что проекция вектора на ось равна сумме проекций его составляющих на ту же ось, и определим a_N как алгебраическую сумму проекций составляющих ax и ay на нормаль к траектории точки. Выберем за положительное направление нормали то, которое получается от поворота положительного направления касательной на прямой угол против хода часов (см. рис. 91) в сторону вогнутости кривой.
Как видно из чертежа (см. рис. 91, б)

Подставляем значения (62) направляющих косинусов:

(72)

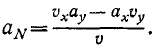
По этой формуле удобно вычислять нормальное ускорение точки, если ее движение задано в координатной форме уравнениями (58′) и (58″).

Эту же формулу (72) можно получить, спроецировав полное ускорение а на нормаль M_n (рис. 91, а):

Подставляя эти значения и сокращая на а, получим:

Задача №4

Движение точки задано уравнениями X= 21,2 sin 2 t, у= 212 cos 2 t. Определить нормальное ускорение точки.

Решение. Дифференцируя эти же уравнения движения при решении задачи № 36 (см. стр. 132), мы уже определили нужные нам величины: υ_x, υ_y, υ, a_x, а_у. Подставляя их в формулу (72), найдем

Ответ. Нормальное ускорение равно нулю.

Задача №5

Точка M движется согласно уравнениям x= r cos πt, y= r sin πt. Найти нормальное ускорение точки М.
Решение. Дифференцируя при решении задачи № 44 (см. стр. 142) эти уравнения движения, мы уже нашли проекции скорости и проекции ускорения. Полную скорость определим по ее проекциям согласно (64):

Подставляя все эти величины в формулу (72), найдем

Ответ. Нормальное ускорение равно rπ 2 .

Чтобы преобразовать формулу (72) для случая, когда движение точки задано в естественной форме, припомним из курса высшей математики выражение кривизны плоской кривой, представленной в параметрической форме уравнениями (58′) и (58″),

Если параметр t означает время, то эту геометрическую формулу можно переписать в обозначениях кинематики:
(73)

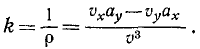
Сравнивая равенства (72) и (73), находим

(74)

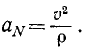
Мы получили положительное значение проекции, следовательно, нормальное ускорение направлено от точки M в положительном направлении оси M_n (см. рис. 91), т. е. в ту сторону от касательной, по которую лежит траектория точки.

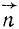
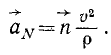
Чтобы получить нормальное ускорение в векторном выражении, надо (74) умножить на единичный вектор нормали:

(74 / )

Как уже было сказано, нормальное ускорение не влияет на величину скорости, потому что оно направлено перпендикулярно к скорости. Оно влияет на направление скорости.

Итак, нормальное ускорение—это проекция ускорения точки на нормаль к траектории, направленная в сторону вогнутости, равная квадрату скорости, деленному на радиус кривизны траектории.
Если движение точки прямолинейное, то радиус кривизны траектории (прямой линии) равен бесконечности, а нормальное ускорение равно нулю.

Обратное заключение можно сделать лишь с некоторой оговоркой: если в каждое мгновение данного промежутка времени нормальное ускорение движущейся точки равняется нулю, то точка движется по прямой; если же нормальное ускорение точки не постоянно равно нулю, а только в какое-либо мгновение, то движение точки не а потому

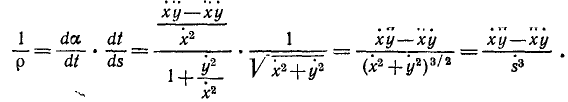
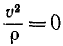
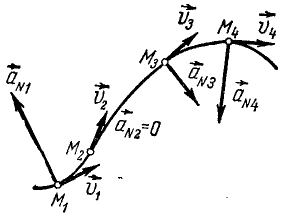
является прямолинейным и равенство означает, что в это мгновение положение точки совпадает с точкой перегиба траектории или же направление скорости меняется на обратное. На чертеже (рис. 93) изображено нормальное ускорение точки в различных местах траектории при равномерном движении.

Рис. 93

Величина ускорения точки равна квадратному корню из суммы квадратов касательного и нормального ускорений:

Видео:Кинематика точки Задание К1Скачать

Ускорение при естественном способе задания движения

Если движение точки задано в естественной форме, то проекции ускорения на нормаль и на касательную можно определить по формулам (69) и (74) и по проекциям определить величину полного ускорения точки (см. рис. 91):

(75)

(75 / )

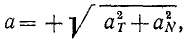
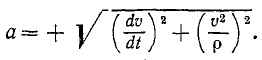
Перед радикалом стоит знак « + », потому что величина ускорения существенно положительна.

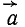
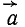
Вектор полного ускорения направлен по диагонали прямоугольника, построенного на векторах касательного и нормального ускорений. Можно точно установить направление ускорения по тангенсу угла, составляемого им с нормалью к траектории:

Касательное ускорение направлено по касательной к траектории, а нормальное к центру кривизны траектории, поэтому вектор полного ускорения лежит с той стороны от касательной, с которой расположена траектория точки.

При криволинейном ускоренном движений точки полное ускорение составляет со скоростью острый угол, а при замедленном—тупой.

Вектор ускорения лежит в соприкасающейся плоскости, и проекция ускорения на бинормаль равна нулю:

Разложение ускорения при движении точки по кривой двоякой кривизны. Если кривая не лежит в одной плоскости, то ее называют пространственной кривой, или кривой двоякой кривизны. В каждой точке к кривой можно провести только одну касательную и бесчисленное множество нормалей, расположенных в плоскости, перпендикулярной к касательной и называемой нормальной плоскостью (рис. 94).

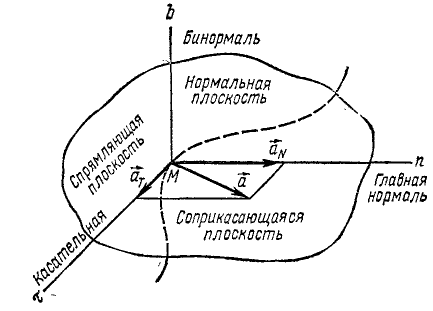
рис. 94

Пусть в мгновение t точка занимает на кривой двоякой кривизны положение М. В это мгновение скорость точки направлена по касательной к кривой в точке М. Через эту касательную и через близкую точку M₁ (не показанную на чертеже)., в которую движущаяся точка придет в мгновение t + Δt, проведем плоскость и будем стремить Δt к нулю. Тогда точка M₁ будет стремиться к точке М. При этом плоскость будет поворачиваться около касательной, проведенной в точке М и стремиться к некоторому определенному положению, в котором она называется соприкасающейся плоскостью. Следовательно, в соприкасающейся плоскости находится вектор скорости движущейся точки в то мгновение, когда эта точка совпадает с точкой М, а также когда она занимает положение, предельно близкое к точке M. А так как ускорение характеризует изменение скорости в данное мгновение, то вектор ускорения тоже находится в соприкасающейся плоскости.

Плоскость, проведенную через точку M перпендикулярно к соприкасающейся и к нормальной плоскостям, называют спрямляющей плоскостью.

Нормаль, лежащую в спрямляющей плоскости, называют бинормалью, а нормаль, лежащую в соприкасающейся плоскости,—главной нормалью (главную нормаль плоской кривой обычно называют просто нормалью).

Касательная Mτ главная нормаль M_n и бинормаль M_b пересекаются в точке M под прямыми углами. Эти три взаимно перпендикулярные прямые в механике часто принимают в качестве координатных осей и называют естественными осями, или осями натурального триэдра. По мере движения точки по траектории естественные оси движутся вместе с ней, поворачиваются относительно основных (неподвижных) осей xOyz.

Положительные направления на естественных осях примем такими, чтобы трехгранный угол τMnb можно было привести в совпадение с углом xОyz. Касательная Mτ играет роль оси Ох, главная нормаль Mn— оси Oy и бинормаль Mb— оси Oz.

Так как вектор ускорения лежит в соприкасающейся плоскости τМn, а бинормаль Mb перпендикулярна к соприкасающейся плоскости, то проекция ускорения на бинормаль всегда равна нулю (α_b = 0), и при проецировании ускорения на три естественные оси мы имеем только две проекции: касательное ускорение и нормальное ускорение.

Таким образом, мы установили, что формулы (69), (69′) и (69″) касательного ускорения, формулы (74) и (74′) нормального ускорения, а также формулы (75) и (75′) полного ускорения, выведенные нами в предположении, что точка движется по плоской траектории, остаются справедливыми для любого движения точки.

Именно потому, что проекция ускорения на бинормаль всегда равна нулю, в формуле (75) величина полного ускорения определяется по двум проекциям, а не по трем, как это имеет место в формуле (66). Приравнивая выражение (66) модуля полного ускорения точки через проекции на неподвижные оси координат его же выражению (75) через проекции на естественные оси, получим для движения точки по любой траектории соотношение

(76)

(76 / )

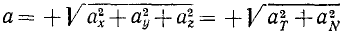
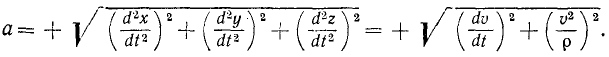
Эти равенства часто бывают полезны при решении задач.

Задача №6

Найти касательное и нормальное ускорения точки, движение которой выражается уравнениями:

Решение. Найдем проекции скорости и ускорения на оси координат:

Подставляя найденные величины в (68), найдем касательное ускорение

Подставляя те же величины в формулу (72), найдем нормальное ускорение

Нормальное ускорение всегда направлено во внутрь траектории, отрицательный знак получился потому, что в этой задаче естественные оси взяты по левой системе, (ось М,— вправо, ось M_n — вниз), а неподвижные — по правой.

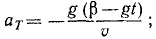
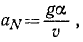
Ответ. где υ — скорость точки.

Задача №7

Найти скорость, полное, касательное и нормальное ускорения точки, описывающей фигуру Лиссажу, по уравнениям движения точки, заданным в координатной форме:

х= 3 sin 2t, у = 4 sin 2t.

Решение. Найдем сначала проекции скорости:

υ_χ = 6 cos 2t, υ_y = 8 cos 2t.

Затем определим величину полной скорости точки:

Для определения касательного и нормального ускорений определим проекции ускорения на декартовы оси координат, затем найдем полное ускорение и разложим его на касательное и нормальное. Имеем

Найдем сначала касательное ускорение, для чего продифференцируем по времени полную скорость или воспользуемся формулой (68):

Мы видим, что полное ускорение по величине равно касательному ускорению, т. е. что нормальное ускорение равно нулю. Это возможно только в случае, если траектория — прямая линия. Для проверки можно определить кривизну траектории или найти уравнение траектории. По первому способу имеем

По второму способу найдем 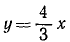(прямая).

Ответ. υ=10 cos 2t; α = 20 sin 2t; а_т= —20sin 2t; α_N = 0.

Задача №8

Точка обода колеса, катящегося без скольжения и без буксования по прямолинейному рельсу, движется согласно уравнениям x=r (ct-sin сt), y=r(l — cos ct). Найти нормальное ускорение точки.
Решение. Для решения задачи можно наметить следующий путь: найти проекции скорости, величину полной скорости, проекции ускорения и полное ускорение; затем, продифференцировав по времени величину полной скорости, найти касательное ускорение и, вычитая его геометрически из полного, найти нормальное.

Дифференцируя уравнения движения, найдем

Далее получаем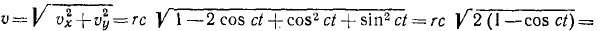

Дифференцируя проекции скорости, найдем

a_x = rc 2 sin ct, a_y = rc 2 cos ct

Дифференцируя υ, найдем касательное ускорение:

Вектор aτ перпендикулярен вектору 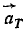и в сумме с ним равняется вектору полного ускорения, поэтому

Задачи такого типа быстрее и короче решать с применением формулы (72). По этой формуле непосредственно получаем:

Ответ:

Задача №9

Тяжелое тело, размерами которого можно пренебречь, брошено с большой высоты с горизонтальной скоростью υ₀ и движется согласно уравнениям x-υ₀t, 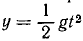. Найти траекторию, скорость, касательное и нормальное ускорения в любом положении, выразив их через скорость тела в этом положении.

Решение. Определяя из первого уравнения t и подставляя во второе, найдем уравнение траектории:

Траектория—парабола (рис. 95). Дифференцируя уравнения движения по времени, найдем проекции скорости и по ним полную скорость:

В начальное мгновение (t = 0), скорость точки υ = υ_o, а затем с течением времени величина скорости непрерывно возрастает. Из полученного равенства определим время t, в течение которого тело приобретает скорость у:

Вторично дифференцируя уравнения движения точки, найдем проекции ускорения на оси координат и полное ускорение:

В данном случае тело движется с постоянным по модулю и направлению ускорением, параллельным оси Оу.
Обращаем внимание на то, что, хотя здесь a = const, движение точки не является равнопеременным, так как условием равнопеременного движения является не условие a = const, а условие a_т= const. В данном же случае, как мы сейчас увидим, а_т непостоянно.

Дифференцируя величину полной скорости по времени или непосредственно по (68), получим касательное ускорение

Подставляя вместо t найденное нами значение, выразим касательное ускорение a_т через скорость υ:

Отсюда следует, что в начальное мгновение, когда υ = υ₀, a_т=0. Затем с увеличением υ величина а_т растет и в пределе стремится к полному ускорению g.
Для нахождения нормального ускорения обратимся к (72). Имеем

В начальное мгновение (при t = 0 и υ=v₀) a_N=g, а затем с увеличением υ а_N убывает, стремясь в пределе к нулю.
Ответ. Парабола

Задача №10

Определить радиус кривизны траектории точки в начале движения, если уравнения ее движения имеют вид: x = 2t, y = t 2 (t— в cек; х, у— в м).
Решение. Из формулы кривизны (73) имеем

Для получения проекций скорости и ускорения в начальное мгновение продифференцируем уравнения движения и подставим t = 0:

Полную скорость в начальное мгновение определяем по ее проекциям:

Подставляя эти величины в формулу (73), получим ответ.
Ответ. р = 2 м

Задача №11

Через 20 сек после начала движения автомобиль, двигаясь иа закруглении радиуса 400 м, приобрел скорость 108 км/ч. Считая, что величина скорости автомобиля пропорциональна квадрату времени, определить полное ускорение автомобиля в конце 20-й секунды н пройденное за это время расстояние.
Решение. За единицы принимаем метр и секунду. Траектория задана—дорога с закруглением радиуса 400 м, и для решения задачи необходимо определить Уравнение движения автомобиля по траектории. (Применять формулы (71) здесь нельзя, так как при равиоперемениом движении величина скорости пропорциональна времени, а в данной задаче она пропорциональна квадрату времени.)
В условии дано

υ=bt 2 .

Найдем коэффициент пропорциональности

Выражая скорость по (53) и разделяя переменные, получим

откуда, интегрируя, получаем

Постоянную C определим из начальных данных: в начальное мгновение (t = 0) автомобиль не прошел еще никакого расстояния, а потому C = 0. Дважды дифференцируя по времени полученное уравнение, найдем касательное ускорение

или в конце 20-й секунды

Скорость в конце 20-й секунды была 30 м/сек, и по (74)

Полное ускорение в конце 20-й секунды было

Чтобы определить расстояние, пройденное автомобилем за 20 сек, положим в уравнении движения t = 20 сек:

Ответ. а = 3,75 м/сек 2 , s = 200 м.

Рекомендую подробно изучить предмет:

Теоретическая механика

Ещё лекции с примерами решения и объяснением:

Основные законы динамики
Колебания материальной точки
Количество движения
Момент количества движения
Приведение системы сил к данной точке
Система сил на плоскости
Естественный и векторный способы определения движения точки
Координатный способ определения движения точки

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.