Уровни изменения каждого фактора это константы предельные значения или коэффициенты уравнения (5 видео)

Уровни изменения каждого фактора это константы предельные значения или коэффициенты уравнения

Содержание

Уровни изменения каждого фактора – это:
Если у Вас нет времени или желания, сдавать тесты при помощи нашего сайта, напишите нам и Мы сделаем это за Вас. — ОСТАВИТЬ ЗАЯВКУ
КОДИРОВАНИЕ ФАКТОРОВ. ВЫБОР ОСНОВНЫХ ФАКТОРОВ И ИХ УРОВНЕЙ
Разница между коэффициентом реакции и константой равновесия
Видео:
Содержание:
Основное отличие — коэффициент реакции от константы равновесия
Ключевые области покрыты
Что такое коэффициент реакции
Что такое константа равновесия
Связь между коэффициентом реакции и константой равновесия
Разница между коэффициентом реакции и константой равновесия
Определение
заявка
Детали Направления
Значение
Заключение
Видео:

Видео:Программирование 1С. Урок 3. Объекты 1С. КонстантыСкачать

Уровни изменения каждого фактора – это:

Выберите один ответ:

b. коэффициенты уравнения

c. предельные значения

ОТВЕТ предоставляется за плату. Цена 3 руб. ВОЙТИ и ОПЛАТИТЬ

Если у Вас нет времени или желания, сдавать тесты при помощи нашего сайта, напишите нам и Мы сделаем это за Вас. — ОСТАВИТЬ ЗАЯВКУ

МЫ ТАКЖЕ МОЖЕМ ВЫПОЛНИТЬ ПРАКТИЧЕСКИЕ ЗАДАНИЯ , ПО ЛЮБОМУ ПРЕДМЕТУ — ОСТАВИТЬ ЗАЯВКУ

НА РЕШЕНИЕ ТЕСТОВ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ, ДЕЙСТВУЕТ ГАРАНТИЯ » ЛУЧШЕЙ ЦЕНЫ «, напишите нам, кто Вам предлагает дешевле чем у нас и где Вам это предлагают, мы проверим и если информация подтвердится, мы сделаем дешевле чем у них.

Видео:РЕГРЕССИОННЫЙ АНАЛИЗ этапы | АНАЛИЗ ДАННЫХ #17Скачать

КОДИРОВАНИЕ ФАКТОРОВ. ВЫБОР ОСНОВНЫХ ФАКТОРОВ И ИХ УРОВНЕЙ

В качестве факторов можно выбирать только контролируемые и управляемые переменные, т.е. такие, которые исследователь может поддерживать постоянными в течение каждого опыта на заданном уровне. В число факторов должны быть включены параметры процесса, оказывающие наиболее сильное влияние на функцию отклика. Необходимо заметить, что, несмотря на всю заманчивость и очевидное преимущество активного спланированного эксперимента перед пассивным, в его применении имеется целый ряд трудностей, связанных с определенными ограничениями на его реализацию. Важнейшим условием применимости этого подхода является управляемость процессов по каждому из выбранных факторов, т.е. возможность независимого изменения каждого из этих факторов и поддержания его на заданном уровне в период проведения опытов.

Для каждого фактора необходимо указать интервал изменения параметров, в пределах которого ставится исследование. Для этого на основе априорной информации устанавливаются ориентировочные значения факторов х_10, х_20,…, х_i_0,…, х_k_0. Этой комбинации значений факторов соответствует точка в многомерном факторном пространстве, которая принимается за исходную точку. Координаты этой точки принимаются за основной (нулевой) уровень.

Интервалом варьирования факторов называется некоторое число (каждое для соответствующего фактора), прибавление которого к основному уровню дает верхний, а вычитание – нижний пределы [2, 11]. Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по осям выбираются так чтобы верхний уровень составлял +1, нижний -1, а основной – 0.

Для факторов с непрерывной областью определения это достигается с помощью преобразования (кодирования) факторов.

В теории планирования экспериментов показано, что минимально необходимое число уровней факторов на единицу больше порядка уравнения.

Для простоты изложения примем, что y=f(x_1,x₂).

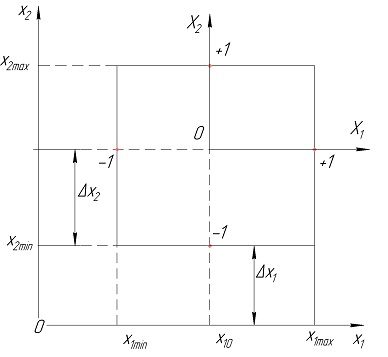
Пусть каждому фактору соответствует координатная ось (это можно сделать, так как факторы независимы). Образованное таким образом пространство называется факторным (рис.3.1) [2, 11].

Рис. 3.1 Переход от реальных факторов к кодированным

Отметим диапазоны изменения факторов: x_i _min – нижний уровень; x_i _max – верхний уровень; i=1,2. Найдем середины этих диапазонов — основные уровни [2, 11]:

(3.7)

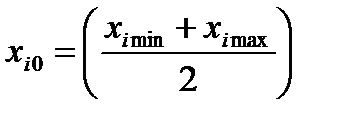
и шаг варьирования фактора:

(3.8)

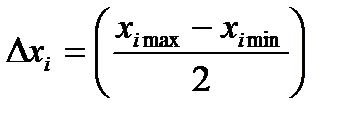
Перенесем начало координат в точку 0 (х_10,х₂₀) и перейдем к новым координатам по формуле:

. (3.9)

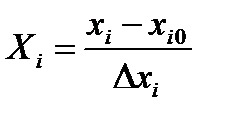
Назовем X_i – кодированными координатами. В кодированном виде верхний уровень любого фактора имеет значение «+1», нижний – «-1», основной – «0». Кодирование уровней факторов проводится для удобства записи условий эксперимента и обработки экспериментальных данных.

3.2.2. МЕТОД ПОЛНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА [2, 9, 10]

Рассмотрим случай, когда функция отклика линейно зависит от трех независимых факторов. План эксперимента представлен в табл. 3.1.

План эксперимента для трех факторов

Номер опыта	план	Результат y_i
X₀	X₁	X₂	X₃	X₁*X₂	X₁*X₃	X₂ *X₃	X₁* X₂ *X₃
+1	-1	-1	-1	+1	+1	+1	-1	y₁
+1	+1	-1	-1	-1	-1	+1	+1	y₂
+1	-1	+1	-1	-1	+1	-1	+1	y₃
+1	+1	+1	-1	+1	-1	-1	-1	y₄
+1	-1	-1	+1	+1	-1	-1	+1	y₅
+1	+1	-1	+1	-1	+1	-1	-1	y₆
+1	-1	+1	+1	-1	-1	+1	-1	y₇
+1	+1	+1	+1	+1	+1	+1	+1	y₈

Здесь добавлен столбец фиктивной переменной X₀, нужный для оценки свободного члена b₀. После реализации получают 8 уравнений с 8 неизвестными, их решение и даст оценку всех восьми коэффициентов регрессии b₀,b₁,…, b₃,b₁₂,…, b_123.

План, в котором число опытов равно числу определяемых коэффициентов, называется насыщенным.

В данном плане были использованы все точки с «крайними» координатами, т.е. 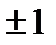(все возможные комбинации выбранных уровней: 2 k =8 (k – число факторов)). Если эксперименты проводятся только на двух уровнях (при двух значениях факторов) и при этом в процессе эксперимента осуществляются все возможные неповторяющиеся комбинации из k факторов, то постановка опытов по такому плану носит название полного факторного эксперимента (ПФЭ) или 2 k

Таким образом, полный факторный эксперимент (ПФЭ) – это эксперимент, реализующий все возможные неповторяющиеся комбинации уровней независимых факторов.

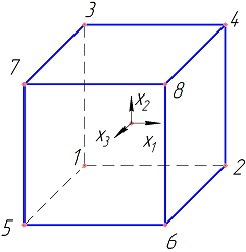
Кодированный план геометрически может быть интерпретирован в виде куба, восемь вершин которого представляют собой восемь экспериментальных данных (рис. 3.2).

При числе факторов k=2 построение матрицы ПФЭ не вызывает затруднений, при увеличении же числа факторов возникает необходимость в некоторых специальных приемах построения матрицы.

Например, прием основанный на чередовании знаков: в первом столбце (для X₁) знаки чередуются поочередно. Во втором (для X₂) – через 2 знака, в третьем (для X₃) – через 4 знака и т.д. по степеням 2 k .

Рис. 3.2. Геометрическое изображение ПФЭ

Матрица ПФЭ обладает следующими свойствами:

— Свойство симметричности: алгебраическая сумма элементов вектор – столбца каждого фактора равна нулю (за исключением столбца, соответствующего свободному члену):

, (3.10)

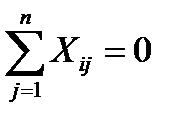
где i- номер фактора; j–номер опыта.

— Свойство нормирования: сумма квадратов элементов каждого столбца равна числу опытов:

; (3.11)

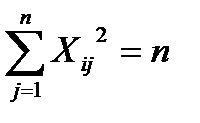
— Свойство ортогональности: скалярное произведение всех вектор-столбцов (сумма почленных произведений элементов любых двух вектор-столбцов матрицы) равно нулю:

(3.12)

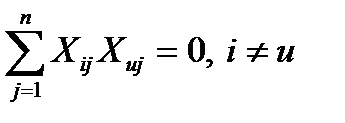
Планы, для которых выполняется свойство 3, называется ортогональными. Благодаря этому свойство резко уменьшаются трудности, связанные с расчетом коэффициентов уравнения регрессии.

Поскольку результаты наблюдений отклика носят случайный характер, приходится в каждой точке плана проводить не один, а m* параллельных опытов (обычно m*=2 4).

В каждой серии экспериментов их последовательность рандомизируется, т.е. с помощью таблиц случайных чисел определяется случайная последовательность реализации экспериментов. Рандомизация дает возможность свести эффект некоторого случайного фактора к случайной погрешности. Это позволяет в определенной степени исключить предвзятость и субъективизм исследователя. Пусть, например, требуется рандомизировать 8 опытов, обозначенных цифрами I,II,…,VIII. Поставим им в соответствие любые 8 последовательных чисел, взятых в любой строке или в любом столбце таблицы случайных чисел. Если при этом встретятся повторяющиеся числа, то их следует отбросить. Например, могут быть получены следующие пары: I – 60; II – 12; III – 05; IV – 15; V – 34; VI – 30, VII – 18, VIII — 70.Расположив случайные числа в порядке возрастания (или убывания), получим искомую последовательность реализации опытов: III, II, IV, VII, VI, V, I, VIII (или VIII, I, V, VI, VII, IV, II, III).

Видео:Примеры решения задач на водородный показатель pH растворов. 11 класс.Скачать

Разница между коэффициентом реакции и константой равновесия

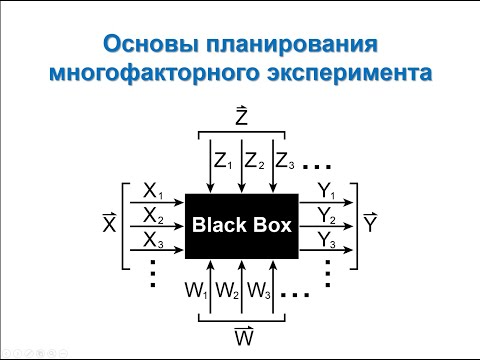
Видео:ММХ. Модуль 8. Основы планирования многофакторного экспериментаСкачать

Видео:

Видео: Химическое равновесие. Константа равновесия. 10 класс.

Видео:Предельные вероятности состоянийСкачать

Содержание:

Видео:Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Основное отличие — коэффициент реакции от константы равновесия

Все химические реакции, которые происходят в системе, могут быть распознаны как равновесные или неравновесные реакции. Реакция становится равновесной, когда реагенты не полностью диссоциируют на свои ионы. Неравновесные реакции включают полную ионизацию реагентов. Коэффициент реакции и константа равновесия — два термина, используемые для объяснения химических реакций, происходящих в системе. Коэффициент реакции дает представление о количестве химических веществ, присутствующих в реакционной смеси. Константа равновесия — это соотношение между концентрациями продуктов и концентрациями реагентов. главное отличие между коэффициентом реакции и константой равновесия является то, что Коэффициент реакции может быть рассчитан для реакции в любое время, тогда как константа равновесия рассчитывается в точке равновесия.

Ключевые области покрыты

1. Что такое коэффициент реакции
— определение, уравнение для расчета, примеры
2. Что такое константа равновесия
— определение, применение, примеры
3. Какова связь между коэффициентом реакции и константой равновесия?
— объяснения соотношения
4. В чем разница между коэффициентом реакции и константой равновесия
— Сравнение основных различий

Ключевые слова: равновесие, константа равновесия, ионизация, реагенты, коэффициент реакции, стехиометрия

Видео:Эконометрика. Множественная регрессия и корреляция.Скачать

Что такое коэффициент реакции

Коэффициент реакции — это соотношение между концентрациями продуктов и концентрациями реагентов. Это может быть сокращено математически, как показано ниже. Давайте рассмотрим следующую реакцию.

Коэффициент реакции для этой реакции может быть дан как ниже. При написании коэффициента реакции следует также учитывать стехиометрию компонентов. Здесь также учитывается стехиометрический коэффициент, который показывает соотношение компонентов. Концентрация повышается до степени этого коэффициента.

Коэффициент реакции для вышеуказанной реакции,

Коэффициент реакции (Qc) = [NH_{3 (г)}] 2 / [N_{2 (г)}] [H2 _(г)] 3

Коэффициент реакции может быть рассчитан в любое время реакции. Это означает, что коэффициент реакции системы может быть рассчитан для реакции до того, как она достигнет равновесия, когда изменение равновесия уже выполнено или когда реакция находится в равновесии.

Вместо концентрации компонентов можно также использовать «активность» каждого компонента для расчета коэффициента реакции. Активность вещества описывает химический потенциал этого вещества.

Видео:Регрессионный анализСкачать

Что такое константа равновесия

Константа равновесия — это соотношение между концентрациями продуктов и концентрациями реагентов в равновесии. Этот термин используется только с реакциями, которые находятся в равновесии. Коэффициент реакции и константа равновесия одинаковы для реакций, находящихся в равновесии.

Константа равновесия также дается как концентрации, возведенные в степень стехиометрических коэффициентов. Константа равновесия зависит от температуры рассматриваемой системы, поскольку температура влияет на растворимость компонентов и объемное расширение. Однако уравнение для константы равновесия не включает каких-либо подробностей о твердых веществах, которые находятся среди реагентов или продуктов. Рассматриваются только вещества в жидкой и газообразной фазах.

Например, давайте рассмотрим равновесие между углекислотой и бикарбонат-ионом.

Константа равновесия для вышеуказанной реакции приведена ниже.

Видео:Теория вероятностей #25: Ковариация и корреляция / ковариационная матрицаСкачать

Связь между коэффициентом реакции и константой равновесия

Если значение коэффициента реакции (Q) выше, чем значение константы равновесия (K), реакция благоприятствует реагентам в большей степени, поскольку количество продуктов в системе выше, чем количество реагентов. Затем реакция имеет тенденцию образовывать больше реагентов, чтобы поддерживать равновесие постоянным.
Если Q ниже, чем K, система состоит из большего количества реагентов, чем продуктов. Поэтому реакция имеет тенденцию образовывать больше продуктов, чтобы поддерживать равновесие.
Если Q и K равны, то реакционная смесь находится в равновесии.

Видео:Геометрический смысл производной. Уравнение касательнойСкачать

Разница между коэффициентом реакции и константой равновесия

Определение

Коэффициент реакции: Коэффициент реакции — это соотношение между концентрациями продуктов и концентрациями реагентов.

Константа равновесия: Константа равновесия — это соотношение между концентрациями продуктов и концентрациями реагентов в равновесии.

заявка

Коэффициент реакции: Коэффициент реакции может быть использован для любой точки реакции (до того, как она достигнет равновесия или после).

Константа равновесия: Константа равновесия может использоваться только для точки, в которой реакции находятся в равновесии.

Детали Направления

Коэффициент реакции: Коэффициент реакции дает представление о направлении, в котором будет протекать реакция.

Константа равновесия: Константа равновесия не дает никаких подробностей о направлении, в котором будет протекать реакция.

Значение

Коэффициент реакции: Значение коэффициента реакции время от времени отличается во время прохождения реакции.

Константа равновесия: Значение константы равновесия является постоянным для конкретного равновесия при определенной температуре.

Заключение

Существует четкое различие между коэффициентом реакции и константой равновесия, хотя оба выглядят одинаково. Это связано с тем, что коэффициент реакции включает концентрацию компонентов в любой точке реакции, тогда как константа равновесия включает концентрации каждого компонента в равновесии. Поэтому очень важно использовать правильные детали для каждого термина этих реакций.