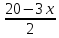Урок по теме уравнение с двумя переменными 7 класс мерзляк (6 видео)

Конспект урока математикм в 7 классе по теме «Системы двух линейных уравнений с двумя переменными»
план-конспект урока по алгебре (7 класс) по теме

Конспект урока изучения нового материала

Содержание

Скачать:
Предварительный просмотр:
Конспект урока по алгебре «Линейное уравнение с двумя переменными» для 7 класса
Разработка урока алгебры по теме «Уравнения с двумя переменными». 7-й класс
Урок алгебры 7 класс по теме «Уравнения с двумя переменными»
Просмотр содержимого документа «Урок алгебры 7 класс по теме «Уравнения с двумя переменными»»
🎦 Видео

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Скачать:

Вложение	Размер
konspekt_uroka_matematiki_v_7_klasse_po_teme.doc	56 КБ

Видео:Видеоурок ЛИНЕЙНОЕ УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Предварительный просмотр:

Конспект урока математики в 7 классе по теме

«Системы двух линейных уравнений с двумя переменными»

обеспечить овладение учащимися графическим приемом решения системы двух линейных уравнений с двумя переменными.

Развивающие: формировать интеллектуальные способности, в том числе:

умение сравнивать, строить аналоги, выделять главное;
умение обобщать и систематизировать пройденный материал;
развивать логическое мышление, память, воображение, математическую речь;
развивать активную познавательную деятельность.

воспитывать самостоятельность, активность, заинтересованность учащихся на всех этапах урока;
формировать такие качества характера, как усидчивость, настойчивость, целеустремлённость.

Повторение пройденного материала.

1) Придумайте задание к следующей задаче:

В ходе обсуждения на доске появляется запись:

Является (0; 20) Не является

решением (4; 8) решением

уравнения (6; 5) уравнения

2) Придумайте задание к следующей задаче:

(2; 3)

III. Актуализация знаний учащихся

Исаак Ньютон сказал: «Чтобы решить вопрос, относящийся к числам

или к отвлеченным отношениям величин,

нужно лишь перевести задачу с родного языка

на язык алгебраический»

Предлагаю вам задачу из «Всеобщей арифметики» Ньютона:

Лошадь и мул шли бок о бок с тяжелой поклажей на спине. Лошадь жаловалась на свою непомерно тяжелую ношу. “Чего же ты жалуешься? – отвечал ей мул. – Ведь если я возьму у тебя один мешок, ноша моя станет вдвое тяжелее твоей. А вот если бы ты сняла с моей спины один мешок, то твоя поклажа стала бы одинакова с моей”. Скажите же, мудрые математики, сколько мешков несла лошадь и сколько мул?

Заполним две таблицы:

В 2 раза тяжелее, чем поклажа лошади

Получаем систему уравнений:

Моделью данной ситуации стали два уравнения, имеющих одно и то же решение, такую модель называют системой линейных уравнений с двумя переменными.

Решением системы линейных уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение в верное равенство.

Для решения системы линейных уравнений с двумя переменными существует несколько способов, один из них графический. Рассмотрим его.

Учащиеся работают группами, учитель консультирует. Затем в виде контроля используется презентация задачи.

IV. Составить математическую модель одной или нескольких следующих задач:

1) Задача иранского ученого XVI века Бехаэддина: Разделить число 10 на 2 части, разность которых 5.

2) Задача Бхаскары: Некто сказал другу: «Дай мне 100 рупий и я буду богаче тебя вдвое». Друг ответил: «Дай мне только 10 и я стану в 6 раз богаче тебя». Сколько рупий было у каждого?

3) Задача из книги «Математика в девяти книгах»: Сообща покупают курицу. Если каждый внесет по 9 (денежных единиц), то останется 11, если же каждый внесет по 6, то не хватит 16. Найти количество людей и стоимость курицы.

4) Задача из рассказа А.П.Чехова «Репетитор»: Купец купил 138 аршин черного и синего сукна за 540 рублей. Спрашивается, сколько аршин он купил того и другого, если синее сукно стоило 5 рублей за аршин, а черное 3 рубля?

5) Задача Ал-Хорезми: Найти два числа, зная, что их сумма равна 10, а отношение 4.

Видео:Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Конспект урока по алгебре «Линейное уравнение с двумя переменными» для 7 класса

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Видеолекции для
профессионалов

Свидетельства для портфолио
Вечный доступ за 120 рублей
311 видеолекции для каждого

Линейное уравнение с двумя переменными.

УМК: Алгебра 7 класс: учеб. для общеобразовательных организаций / А.Г. Мерзляк, В.Б.Полонский, М.С.Якир. – М.: Вентана – Граф, 2013.

Тема: Линейное уравнение с двумя переменными.

Тип урока : урок формирования умений и навыков.

o знакомство учащихся с понятиями линейного уравнения с двумя переменными и его решения;

o выработка умения выражать одну переменную линейного уравнения с двумя переменными через другую;

o развитие познавательных навыков обучающихся, критического и творческого мышления;

o воспитание познавательного интереса к математике, настойчивости, целеустремленности в учебе.

Личностные : ф ормирование навыков организации анализа своей деятельности объективной самооценки и взаимооценки.

Предметные: формирование знаний о линейном уравнении с двумя переменными, его решении и свойствах.

Познавательные: осуществление поиска нужной информации в учебном пособии; понимание знаков, символов, умение их применять; понимание заданного вопроса, в соответствии с ним построение устного ответа; выдвижение и обоснование гипотез, предложение способов их проверки.

Регулятивные: сопоставление способов и результата своих действий с заданным эталоном.

Коммуникативные: умение устанавливать рабочие отношения; эффективно сотрудничать.

Оборудование: компьютер, мультимедийный проектор, экран.

I Организационный момент (Приветствие. Проверка готовности учащихся к уроку). Мотивация

Я хочу загадать вам загадку:

Что самое быстрое, но и самое медленное.

Самое большое, но и самое маленькое.

Самое продолжительное, но и самое краткое.

Самое дорогое, но и дёшево ценимое нами?

Это ребята – время. Урок длится всего 45 мин, и мне бы очень хотелось, чтобы они были потрачены с пользой.

II. Проверка домашнего задания

Какую тему мы с вами изучили на предыдущих уроках? (Уравнения с двумя переменными.)

Давайте проверим ваше домашнее задание.

III. Повторение пройденного материала. Актуализация опорных знаний учащихся.

На доске записано:5х; 5х + 7, 5х + 7 = 12.

— Дайте определение записанным выражениям.

— Что называется уравнением?

— Сформулируйте определение линейного уравнения с одной переменной.

— Что значит решить уравнение?

— Что называется корнем уравнения?

— Приведите свой пример линейного уравнения с одной переменной.

— Чем отличаются уравнения 5х+7=12 и 5х+7у=12?

— Как называется первое уравнение?

— Попытайтесь сформулировать определение второго уравнения.

— Как ы думаете, какова тема нашего сегодняшнего урока? Запишем тему урока в тетради.

— Давайте попробуем провести параллель между известным нам материалом и новым.

I V. Изучение нового материала.

— Давайте вспомним всё, что мы знаем о линейных уравнениях.

— Какой тип уравнения нам известен? (линейное уравнение с одной переменной)

— Вспомним определение линейного уравнения с одной переменной.

— Что называется корнем линейного уравнения с одной переменной?

— Сформулируем все свойства линейного уравнения с одной переменной.

— Заполним первую строку таблицы.

Что является решением уравнения

Линейное уравнение с одной переменной.

ах=в, где х – переменная, а,в- числа.

Значение х, при котором уравнение обращается в верное равенство

1) перенос слагаемых из одной части уравнения в другую, изменив их знак на противоположный.

2) умножение и деление обеих частей уравнения на одно и тоже, не равное нулю число.

Линейное уравнение с двумя переменной.

где х,у – переменные, а,в.с – некоторые числа.

Значения х, у, при которых уравнение обращается в верное числовое равенство.

3) равносильность уравнений.

— Приведите пример уравнения с двумя переменными. (Записать в тетради)

— Что бы вам хотелось узнать о линейном уравнении с двумя переменными?

— Попробуйте сформулировать цель урока. (Совместно с учениками поставить задачи и вопросы к уроку)

Возможные ответы учащихся: знать определение линейно гоуравнения с двумя переменными; научиться находить линейные уравнения 2 степени среди других уравнений; выяснить как решаются эти уравнения.

— Давайте вместе искать ответы на поставленные вами вопросы.

Линейным уравнением с двумя переменными называется уравнение вида ax + by = c, где a,b и c – некоторые числа, а x и y –переменные.

— Среди данных уравнений найдите линейные уравнения с 2 переменными и назовите коэффициенты а, в, с: а) 6х = 96; б) 7х-5у = 2; в) 4х + 3у⁷; г) х + у = 15; д) х-у = 3.

— Линейные уравнения с двумя переменными, как и все уравнения надо решать.

— Найдите корни уравнения х-у = 12

— Сколько решений имеет это уравнение? (Множество)

— Как вы нашли корни уравнения? (Подбором)

— Как выяснить будет ли данная пара чисел корнем уравнения? (Проверить подстановкой)

— Уравнение x – y = 12 при x = 8, y =-4 обращается в верное равенство 8 – (-4) = 12. Говорят, что пара значений переменных x = 8, y = -4 является решением этого уравнения). Попробуйте дать определение решения линейного уравнения с двумя переменными? (Дети дают определение)

Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.

Пары значений переменных иногда записывают короче: (х; у) В такой записи на первом месте пишут значение x а на втором — y. Одно из решений рассмотренного уравнения может быть записано в виде (8; -4).

Уравнения с двумя переменными, имеющие одни и те же решения (или не имеющие решений), называются равносильными.

— Приведите примеры равносильных уравнений. (х+у=7 и х=7-у; =-4 и = -2)

Уравнения с двумя переменными обладают такими же свойствами, что и уравнения с одной переменной:

1. Если в уравнении перенести любой член из одной части в другую, изменив его знак, то получится уравнение равносильное данному.

2. Если обе части уравнения умножить или разделить на одно и то же число (не равное нулю), то получится уравнение равносильное данному.

— По аналогии с первой строкой, давайте заполним вторую строку таблицы, тем самым обобщая новый материал.

Рассмотрим уравнение 4x + 2y = 10. Используя свойства уравнений, выразим одну переменную через другую.

Можем выразить переменную х через переменную у. Для этого оставим 4х в левой части уравнения, а 2у перенесем в правую, изменив его знак. Получаем равносильное уравнение 4х = – 2у+10.

Разделим каждую часть этого уравнения на число 4, получим равносильное уравнение

Для того, чтобы выразить переменную у через переменную х, сначала перенесем 4 x из левой части в правую, изменив его знак. Получаем равносильное уравнение 2 y = 1 0 — 4 x.

Разделим каждую часть этого уравнения на число 2, получим равносильное уравнение

Таким образом, мы выразили одну переменную через другую.

Пользуясь этим равенством, для каждого значения x можно вычислить значение y.

Если x = 2, то y = 5 — 2· 2 = 1.

Если x = -2, то y = 5 — 2· (-2) = 9. Пары чисел (2; 1), (-2; 9) – решения данного уравнения. Таким образом, данное уравнение имеет бесконечно много решений.

V. Работа с учебником. Открываем учебники на странице 195.

— Найдите в учебниках место, где выделена главная идея темы нашего урока.

а) Устно выполняем № 28.1, №28.2, №28.4.

б) Письменно решаем № 28.3. Делают в тетрадях самостоятельно, затем на доске.

в) № 28.8(1;4) № 28.10(1;2) Работа в парах. Разбор у доски.

VI. Историческая справка.

Рене Декарт (1596-1650) – французский философ, математик и физик.

Создал основы аналитической геометрии, ввел понятие переменной величины, разработал метод координат. Осуществил связь алгебры с геометрией.

Пьер Ферма (1601-1665) – французский математик, один из создателей аналитической геометрии и теории чисел. Занимался теорией решения алгебраических уравнений с несколькими переменными.

V I . Самостоятельная работа с самопроверкой с помощью экрана в классе.

1. Выпишите линейное уравнение с двумя переменными:

а) 3 + 6у = 5; б) ху = 16; в) 2х – у = 5.

2. Является ли решением уравнения2х — у = 5 данная пара чисел?

3. Выразите из линейного уравнения 3х – 4у = 12

а) х через у б) у через х.

4. Найдите три, каких-либо решения уравнения х + у = 17.

V II . Итог урока. Обобщение пройденного материала на уроке. Выставление оценок.

Давайте попробуем дать ответы на вопросы, поставленные в начале урока.

— Какие уравнения называются линейными с двумя переменными?

— Что значит решить линейное уравнение с двумя переменными?

— Что называется решением уравнения с двумя переменными?

— Можем ли мы найти все решения уравнения? (Нет, так как их бесконечное количество)

— Как записывается корень уравнения?

— Какие уравнения называются равносильными?

— Перечислите свойства линейного уравнения с двумя переменными

V III .Рефлексия. Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:

сегодня я узнал…

я выполнял задания…

я почувствовал, что…

у меня получилось …

IX . Домашнее задание: п.28, № 28.5, №28.11, № 28.51-повтор.

Видео:7 класс, 8 урок, Линейное уравнение с двумя переменными и его графикСкачать

Разработка урока алгебры по теме «Уравнения с двумя переменными». 7-й класс

Разделы: Математика

Класс: 7

Тип урока: урок изучения и первичного закрепления нового материала.

Дидактическая цель: восприятие, осмысление и первичное закрепление новой учебной информации.

Образовательная цель: ввести понятия «уравнение с двумя переменными», «решение линейного уравнения с двумя переменными», показать приемы решения уравнений с двумя переменными, доступные семиклассникам.

Развивающая цель: научить формулировать учебную задачу, выдвигать предположения, распознавать новую и известную информацию.

Воспитательная цель: воспитывать интерес к познанию, культуру общения при групповой и фронтальной работе.

Планируемые результаты

Предметные: научиться распознавать и приводить примеры уравнений с двумя переменными, определять является ли пара чисел решением данного уравнения с двумя переменными и находить какие-нибудь пары решений уравнения, используя свойства уравнений.
Метапредметные:

Познавательные
Структурирование знаний
Осознанное и произвольное построение высказываний
Рефлексия способов действий
Осознанное чтение текста;
Построение логической цепочки рассуждений

Коммуникативные
Корректно и аргументированно отстаивать свою точку зрения;
Критически относиться к своему мнению;
Принимать позицию собеседника;
Организовывать учебное взаимодействие в группе;

Регулятивные
Целеполагание
Планирование
Прогнозирование
Контроль
Коррекция
Оценка
Саморегуляция

Личностные: осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению, ответственное отношение к учению, саморазвитие, самообразование.

Педагогические технологии: развития критического мышления, уровневой дифференциации.

Методы обучения: репродуктивные, частично-поисковый.

Формы организации учебной деятельности: индивидуальная, групповая, фронтальная.

Технологическая карта урока

Деятельность учителя

Деятельность учащихся

Предлагает построить математическую модель реальной ситуации.
Приложение 1.

В группах составляют математическую модель реальной ситуации.

Организует проверку и корректирует формулировку урока.

Соотносят новую модель со своими установившимися представлениями о моделях. Предлагают название новой модели и формулируют тему урока.

Организует работу по заполнению таблицы
«З – Х – У» (знаем – хотим узнать – узнали), актуализирует опыт ученика.
Приложение 2.

Записывают то, что знают по теме и что хотели бы узнать. Высказывают предположения о логике изучения учебного материала.
Приложение 2.

Осмысление новой информации

Применяет прием «ИНСЕРТ»
Предлагает прочитать текст с маркировкой.
«v» — уже знал
«+» — новое
«-» — думал иначе
«?» — не понял, есть вопросы. >
Приложение 3

При чтении текста на полях расставляют пометки. Текст читают индивидуально. Затем обсуждают в группе.

Организует обсуждение маркировки текста

Сравнивают свою маркировку с маркировками других. Получают ответы на вопросы. Задают уточняющие вопросы

Вопросы Блума
Учитель предлагает вопросы и упражнения, оказывает помощь при затруднениях.

Приложение 4.
Примечание: этот прием используется для закрепления базовых знаний и умений. Для развития учащихся с высоким уровнем обучаемости.

Отвечают на вопросы и решают упражнения.
Организуют взаимопроверку и самоконтроль

Организует обсуждение записей в таблице
«З – Х – У».

Приложение 2.
Индивидуально заполняют в таблице графу «узнал». Обсуждают в группе. Затем фронтально корректируют свои записи. Планируют над какой проблемой индивидуально или в группе работать на следующем уроке.

Информация о домашнем задании.

Задает домашнее задание
§ 24, № 911, 916, 929, 936

Записывают домашнее задание.

Литература

А.Г.Мерзляк «Алгебра». 7 класс.
Ирина Муштавинская «Технология развития критического мышления на уроке и в системе подготовки учителя».

Видео:ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Урок алгебры 7 класс по теме «Уравнения с двумя переменными»

Урок алгебры по теме » Линейные уравнения с двумя переменными» разработан в соответствии с требованиями ФГОС, соответствует базовому уровню обучения.

Просмотр содержимого документа
«Урок алгебры 7 класс по теме «Уравнения с двумя переменными»»

Тема: «График линейного уравнения с двумя переменными» Урок № 83. 19.03.19

Цели: Познакомить учащихся с понятиями линейного уравнения с двумя переменными и его решения, научить выражать из уравнения х через у или у через х.

Познавательные: выдвигать и обосновывать гипотезы, предлагать способы их проверки

Регулятивные: сличать способ и результат своих действий с заданным эталоном, обнаруживать отклонения и отличия от эталона; составлять план и последовательность действий.

Коммуникативные: устанавливать рабочие отношения; эффективно сотрудничать и способствовать продуктивной кооперации.

Личностные: формирование навыков организации анализа своей деятельности

Оборудование: компьютер, мультимедийный проектор, экран

Этап мотивации (самоопределения) к учебной деятельности

Анализ контрольной работы № 6 – задание № 5, 2

Этап актуализации и фиксирования индивидуального затруднения в пробном действии

1) Найти числовое значение выражения 5х + 2у при:

а) х = 0; у = -1; б) х = 4; у = 0,5; в) х = -3; у = -2.

2) Найти несколько пар значений х и у, для которых значение выражения 5х + 2у равно 20. 3) Найдите точку пересечения прямых и .
4) Найдите координаты точки пересечения прямой, проходящей через точки А (–2;7) и В(–5;-2), и луча CD, если заданы координаты С (–6;6) и D(3;0) [Ответ: ( – 3; 4)]

Этап выявления места и причины затруднения.

Решите уравнение: 3х – 9 = 0. Давайте вспомним всё, что мы знаем о линейных уравнениях и попробуем провести параллель между известным нам материалом и новым материалом.

Какой тип уравнения нам известен? (линейное уравнение с одной переменной)

Вспомним определение линейного уравнения с одной переменной.

Что называется корнем линейного уравнения с одной переменной?

Сформулируем все свойства линейного уравнения с одной переменной.

Составьте задачу по условию: Петя купил несколько карандашей, а тетрадей на 5 больше. (Тетрадей х, карандашей у, тогда х – у = 5)

Как называется данное выражение?

Сколько переменных в данном уравнении?

Сформулируйте тему урока. А цели?

Этап построения проекта выхода из затруднения

Заполняется 1 часть таблицы

Что является решением уравнения

Линейное уравнение с одной переменной.

ах=в, где х – переменная, а,в- числа.

Значение х, при котором уравнение обращается в верное числовое равенство

1) перенос слагаемых из одной части уравнения в другую, изменив их знак на противоположный.

2) обе части уравнения умножить или разделить на одно и тоже, не равное нулю число.

Линейное уравнение с двумя переменными.

ах + ву = с, где х,у – переменные, а,в.с – числа.

Значения х, у, обращающие уравнение в верное числовое равенство.

Верны свойства 1,2.

3) равносильные уравнения:

Уравнение с двумя переменными.

ах n + ву m = с, где х,у – переменные, а,в.с – числа.

Пример 5 в учебнике стр. 179

После того, как заполнили первую часть таблицы, опираясь на аналогию, начинаем заполнять вторую строку таблицы, тем самым узнавать новый материал.

Этап реализации построенного проекта

Обратимся к теме: линейное уравнение с двумя переменными. Само название темы наталкивает на мысль, что нужно вводить новую переменную, например у.

Сформулируем по аналогии с определением линейного уравнения с одной переменной определение линейного уравнения с двумя переменными (Линейным уравнением с двумя переменными называется уравнение вида ax + by = c, где a,b и c – некоторые числа, а x и y –переменные).

Уравнение x – y = 5 при x = 8, y = 3 обращается в верное равенство 8 – 3 = 5. Говорят, что пара значений переменных x = 8, y = 3 является решением этого уравнения.

— Сформулируйте определение решения уравнения с двумя переменными (Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство)

Пары значений переменных иногда записывают короче: (8;3). В такой записи на первом месте пишут значение x а на втором — y.

Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной:

Если в уравнении перенести любой член из одной части в другую, изменив его знак, то получится уравнение равносильное данному.

Если к обеим частям уравнения прибавить одно и тоже число, то получится уравнение равносильное данному.

Если обе части уравнения умножить или разделить на одно и то же число(не равное нулю), то получится уравнение равносильное данному.

Пример 1. Рассмотрим уравнение 10x + 5y = 15. Используя свойства уравнений, выразим одну переменную через другую.

Для этого сначала перенесем 10x из левой части в правую, изменив его знак. Получаем равносильное уравнение 5y = 15 — 10x.

Разделим каждую часть этого уравнения на число 5, получим равносильное уравнение

у = 3 — 2x. Таким образом, мы выразили одну переменную через другую. Пользуясь этим равенством, для каждого значения x можно вычислить значение y.

Если x = 2, то y = 3 — 2· 2 = -1.

Если x = -2, то y = 3 — 2· (-2) = 7. Пары чисел (2; -1), (-2; 7) – решения данного уравнения. Таким образом, данное уравнение имеет бесконечно много решений.

Пример 2. Мука расфасована в пакеты по 3 кг и по 2 кг. Сколько пакетов каждого вида надо взять, чтобы получилось 20 кг муки?

Допустим, что надо взять x пакетов по 3 кг и y пакетов по 2 кг. Тогда 3x + 2y = 20. Требуется найти все пары натуральных значений переменных x и y, удовлетворяющих этому уравнению. Получаем: 2y = 20 — 3x у =

Подставляя в это равенство вместо x последовательно все числа 1,2,3 и т.д., найдем при каких значениях х, значения y являются натуральными числами.

Получаем: (2;7), (4;4), (6;1). Других пар, удовлетворяющих данному уравнению нет. Значит надо взять либо 2 и 7, либо 4 и 4, либо 6 и 1 пакетов соответственно.

Этап первичного закрепления с проговариванием во внешней речи

Этап включения в систему знаний и повторения: № 913; № 915; № 917

Этап рефлексии учебной деятельности на уроке (вопросы на листе информации )

Домашнее задание: п. 24, № 911, № 914, № 916