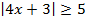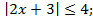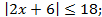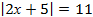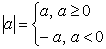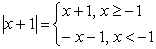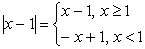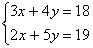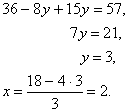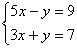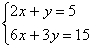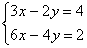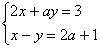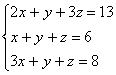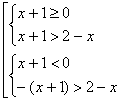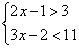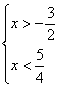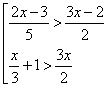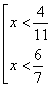план-конспект урока по алгебре (6 класс) на тему
Планирование урока осуществлялось на основе календарно-тематического планирования для 6 класса. Тема урока: «Повторение. Линейные неравенства с одной переменной и их системы». Цель урока: закрепление умения решать линейные неравенства с одной переменной и их системы; развивать логическое мышление, математическую речь, чувство коллективизма.
На данном уроке мною была предложена работа по созданию коллаборативной среды в классе, преодолению барьеров учащихся, развитию их саморегуляции и навыков критического мышления, коммуникативных навыков.
Перед уроком я предложила учащимся выбрать салфетку любого цвета, встречая их у двери. Нам это нужно было для того, чтобы расположить положительно к себе незнакомых мне детей. Для создания благоприятной дружеской атмосферы в классе я предложила создать круг и используя прием «Комплименты», создать атмосферу добра, взаимопонимания, уважения друг к другу. Реакция детей была положительной, ребята с удовольствием дарили друг другу комплименты.
Для создания психологического климата, осознания уникальности каждого ученика начать урок я решила с приема «Мы — уникальны!». Для этого ребята, продолжая работать в кругу, проделали предложенные им операции. Сложите салфетки пополам. Оторвите верхний угол и нижний. Сложите салфетку еще раз и сделайте отверстие посередине. Разверните салфетку, посмотрите на салфетки других. Есть похожие? Ребята смогли убедиться, что у них разные композиции. Значит, каждый из вас имеет уникальное мышление, которое вы сможете реализовать сегодня на уроке. Я считаю, что данный прием в первую очередь позволил создать коллаборативную среду в классе, заинтересовал и повысил мотивацию, так как мы редко начинаем урок, работая в кругу, способствовал высказыванию идей каждого и осознанию их уникальности
Видео:Решение системы линейных неравенств с одной переменной. 6 класс.Скачать
Скачать:
| Вложение | Размер |
|---|---|
| математика 6 класс | 277.04 КБ |
Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Предварительный просмотр:
Анализ урока математики в 6 класс на тему: «Повторение. Линейные неравенства с одной переменной и их системы».
Планирование урока осуществлялось на основе календарно-тематического планирования для 6 класса. Тема урока: «Повторение. Линейные неравенства с одной переменной и их системы». Цель урока: закрепление умения решать линейные неравенства с одной переменной и их системы; развивать логическое мышление, математическую речь, чувство коллективизма.
На данном уроке мною была предложена работа по созданию коллаборативной среды в классе, преодолению барьеров учащихся, развитию их саморегуляции и навыков критического мышления, коммуникативных навыков.
Перед уроком я предложила учащимся выбрать салфетку любого цвета, встречая их у двери. Нам это нужно было для того, чтобы расположить положительно к себе незнакомых мне детей. Для создания благоприятной дружеской атмосферы в классе я предложила создать круг и используя прием «Комплименты», создать атмосферу добра, взаимопонимания, уважения друг к другу. Реакция детей была положительной, ребята с удовольствием дарили друг другу комплименты.
Для создания психологического климата, осознания уникальности каждого ученика начать урок я решила с приема «Мы — уникальны!». Для этого ребята, продолжая работать в кругу, проделали предложенные им операции. Сложите салфетки пополам. Оторвите верхний угол и нижний. Сложите салфетку еще раз и сделайте отверстие посередине. Разверните салфетку, посмотрите на салфетки других. Есть похожие? Ребята смогли убедиться, что у них разные композиции. Значит, каждый из вас имеет уникальное мышление, которое вы сможете реализовать сегодня на уроке. Я считаю, что данный прием в первую очередь позволил создать коллаборативную среду в классе, заинтересовал и повысил мотивацию, так как мы редко начинаем урок, работая в кругу, способствовал высказыванию идей каждого и осознанию их уникальности.
Далее я предложила задание на актуализацию прежних знаний, используя прием «Выбери правильный ответ» ответить на следующие вопросы, которые необходимо применить в решении предложенных мною заданий. Данные ответы учащихся способствовали созданию проблемной ситуации, выхода на тему и постановку целей урока.
На операционном этапе ребятам была предложена работа по технологии КСО методике ВОЗ. Каждому учащемуся необходимо решить 3 карточки и научить решать одноклассников.
После учащимся необходимо было разбиться на группы для решения системы неравенств с одной переменной. Группы отображали решение на ватмане, затем обменивались, и каждой группе необходимо было отметить 3 аспекта:
Далее спикеры каждой из групп должны были выйти к доске и защитить работу, огласив при этом все замечания.
На этапе рефлексии с целью развития критического мышления группам было предложено написать мини — сочинение «Сегодня на уроке Я…».
Для закрепления материала было предложено домашнее задание на решение системы неравенств с одной переменной, причем, каждому разное.
В завершении урока я попросила выстрелить в мишень с помощью стикеров и определить свое настроение.
Таким образом, анализируя данный урок, я считаю, что образовательные цели были достигнуты через решение поставленных задач.
В свою очередь, проведя данный урок, я увидела, что научилась создавать благоприятные условия для положительной, доброжелательной обстановки в классе, применять задания творческого характера для повышения учебной мотивации учащихся, их математической грамотности, организовывать диалогические беседы, развивать их коммуникативные навыки.
Видео:Линейное неравенство с одной переменной. 6 класс.Скачать

Урок «решение Линейных уравнений и неравенств с одной переменной»
6.3В Линейные неравенства с одной переменной
ФИО учителя: Семыкина Л.И.
Решение линейных уравнений и неравенств с одной переменной
6.2.2.3 решать линейные уравнения с одной переменной;
6.2.2.4 решать уравнения вида 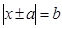
6.2.2.15 изображать множество точек на координатной прямой, заданное неравенством вида | x | > a , | x | ≥ a , | x | a , | x | ≤ a ;
Учащиеся будут: знать как решать линейные неравенства видов kx > b , kx ≥ b , kx b , kx ≤ b , как изображать решения неравенств на координатной прямой. Знают алгоритм решения простейшего линейного уравнения. Учащиеся определяют порядок выполнения действий по приведению заданного уравнения к простейшему линейному. Учащиеся верно выполняют вычисления
Учащиеся знают: как решать линейные неравенства и уравнеия, комментируют решение уравнений и неравенств, используя свойства уравнений и неравенств.
Учащиеся будут: аргументировать свои выводы, работая в группе, при повторении теоретического материала на более высоком уровне;описывать ход своих действий и делать выводы;при устной работе обосновывать ответ, используя терминологию.
Предметная лексика и терминология: неравенство, , решить неравенство.Полезные выражения для диалогов и письма:Решить линейное неравенство, упростить выражение. перенести слагаемые, меняя знак , приводить подобные слагаемые.
Умение учиться, добывать самостоятельно информацию, анализировать ситуацию, адаптироваться к новым ситуациям, ставить проблемы и принимать решения, работать в команде, отвечать за качество своей работы, умение организовывать свое время.
Привитие ценностей осуществляется посредством работ, запланированных на данном уроке.
Взаимосвязь с казахской литературой, с казахским языком.
Знание алгоритма решения линейных неравенств, уравнений
Запланированная деятельность на уроке
Проверить домашнее задание. Совместно с учащимися определить тему и цели урока, «зону ближайшего развития».
Актуализация опорных знаний. Повторение. Устный опрос по правилам.
1 )Какое уравнение с одной переменной называется линейным?
2)Что называется корнем уравнения?
3)Какие уравнения называются равносильными?
4)Что значит решить уравнение?
5)Какие свойства используются при решении уравнений?
6)Какие свойства используются при решении неравенств?
Мозговой штурм. Каждому ряду предлагается одинаковое количество заданий : Выигрывает тот ряд, кто решит первый и разгадает пословицу.
Группа 1. Решите
а) 1-2х 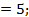
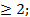
Бақыт кілті — еңбекте. Ключ к счастью — в труде.
Группа 2. Решите
а) 2-5х 
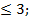
Байлықтың атасы – еңбек, анасы – жер.(Отец богатства – труд, мать богатства – земля).
Группа 3. Решите:
а) 4-5х=14 б) 3х+9 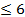
Отансыз адам — ормансыз бұлбұл.Человек без родины своей, как соловей без леса .
Разобрать задания, которые были сделаны с ошибками. Устная взаимопроверка.
Каждый ряд объясняет смысл своей пословицы.
Работа с классом. Основываясь на знания: определение модуля, умение изображать решение неравенства, рассмотреть решение линейного неравенства с одной переменной и линейного уравнения, содержащее переменную под знаком модуля, требующих упрощения .От каждого ряда выходит представитель и показывает свое решение.
1 ряд Решите уравнение:
2 ряд Решите неравенство: 4х – 2·(3-8х) 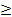
3 ряд Решите уравнение:
Каждый ряд проверяет свое решение.
. Закрепление продолжить организовав работу в паре, что дает возможность каждому оказать помощь с помощью наиболее продвинутых в математике учащихся.
Работа в паре. . Раздать каждой паре карточки с заданиями. Каждая пара выбирает свой уровень.
№1 Решите ненравенство:
а)-3х 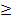
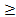
№2 Решите уравнение: а)-3х+2=17; б) 2(х+1)=0
№1 Решите ненравенство:
а)-3 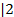
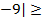
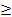
№2 Решите уравнение: а)-3(2х+2)-5=17; б) (2-х)(х+1)=0
Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу, оказывает помощь слабоуспевающим.
Предоставить учащимся достаточно времени для выполнения заданий.
Проводится взаимопроверка по ключу, проводится анализ ошибок. Выслушать выводы учащихся по заданиям.
Рефлексия. Я сегодня все понял» — «Я не понял» — «Есть непонятные моменты» —
Мне стоит обратить внимание-
Домашнее задание. №1082
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
Здоровье и соблюдение техники безопасности. Связи с ИКТ.
На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).
Предусмотрена устная взаимопроверка, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.
Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.
Рефлексия по уроку
Были ли цели урока/цели обучения реалистичными?
Все ли учащиеся достигли ЦО?
Если нет, то почему?
Правильно ли проведена дифференциация на уроке?
Выдержаны ли были временные этапы урока?
Какие отступления были от плана урока и почему?
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.
Урок проведен в соответствии с программными требованиями, достигает поставленной цели, соответствует уровню подготовленности класса, логична последовательность и взаимосвязь этапов урока. Учитель сохраняет преемственность в обучении. Для активизации деятельности на уроке используются различные методы обучения — устные и письменные виды работы. Учитель целенаправленно работает над формированием общих учебных навыков, подбирая различные дифференцированные задания. Но не все учащиеся достигли целей обучения. Есть ученики с очень ослабленным вниманием, плохо развитой памятью, им требуется отдельное внимание.
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?
Что могло бы поспособствовать улучшению урока (подумайте как о преподавании, так и об обучении)?
Что я выявил (а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Урок линейные уравнения и неравенства с одной переменной 6 класс
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Видео:Линейное неравенство с одной переменной. 6 класс.Скачать

«Линейные уравнения и неравенства»
Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.
Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство. Например, число 1 является решением уравнения 2х+5=8х-1. Уравнение х2+1=0 не имеет решения, т.к. левая часть уравнения всегда больше нуля. Уравнение (х+3)(х-4) =0 имеет два корня: х1= -3, х2=4.
Просмотр содержимого документа
«»Линейные уравнения и неравенства»»
Линейные уравнения и неравенства
Романишина Дина Соломоновна, учитель математики гимназии №2 г. Хабаровска
1. Уравнения с одной переменной.
Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.
Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство. Например, число 1 является решением уравнения 2х+5=8х-1. Уравнение х2+1=0 не имеет решения, т.к. левая часть уравнения всегда больше нуля. Уравнение (х+3)(х-4) =0 имеет два корня: х1= -3, х2=4.
Решить уравнение — значит найти все его корни или доказать, что корней нет.
Уравнения называются равносильными, если все корни первого уравнения являются корнями второго уравнения и наоборот, все корни второго уравнения являются корнями первого уравнения или, если оба уравнения не имеют корней. Например, уравнения х-8=2 и х+10=20 равносильны, т.к. корень первого уравнения х=10 является корнем и второго уравнения, и оба уравнения имеют по одному корню.
При решении уравнений используются следующие свойства:
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получите уравнение, равносильные данному.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Уравнение ах=b, где х – переменная, а и b – некоторые числа, называется линейным уравнением с одной переменной.
Если а¹0, то уравнение имеет единственное решение 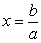
Если а=0, b=0, то уравнению удовлетворяет любое значение х.
Если а=0, b¹0, то уравнение не имеет решений, т.к. 0х=b не выполняется ни при одном значении переменной.
Пример 1. Решить уравнение: -8(11-2х)+40=3(5х-4)
Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с х в левую часть уравнения, а слагаемые, не содержащие х, в правую часть, получим:
Пример 2. Решить уравнения:
Эти уравнения не являются линейными, но покажем, как можно решать такие уравнения.
3х2-5х=0; х(3х-5)=0. Произведение равно нулю, если один из множителей равен нулю, получаем х1=0; х2=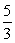
Ответ: 0; 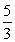
Разложить на множители левую часть уравнения:
х2(х-2)-9(х-2)=(х-2)(х2-9)=(х-2)(х-3)(х-3), т.е. (х-2)(х-3)(х+3)=0. Отсюда видно, что решениями этого уравнения являются числа х1=2, х2=3, х3=-3.
с) Представим 7х, как 3х+4х, тогда имеем: х2+3х+4х+12=0, х(х+3)+4(х+3)=0, (х+3)(х+4)=0, отсюда х1=-3, х2=- 4.
Ответ: -3; — 4.
Пример 3. Решить уравнение: ½х+1ç+½х-1ç=3.
Напомним определение модуля числа:
Например: ½3½=3, ½0½=0, ½- 4½= 4.
В данном уравнении под знаком модуля стоят числа х-1 и х+1. Если х меньше, чем –1, то число х+1 отрицательное, тогда ½х+1½=-х-1. А если х-1, то ½х+1½=х+1. При х=-1 ½х+1½=0.
Таким образом,
Аналогично
а) Рассмотрим данное уравнение½х+1½+½х-1½=3 при х£-1, оно равносильно уравнению -х-1-х+1=3, -2х=3, х=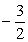
b) Пусть -1 х £ 1, тогда данное уравнение равносильно уравнению х+1-х+1=3, 2¹3 уравнение не имеет решения на данном множестве.
с) Рассмотрим случай х1.
х+1+х-1=3, 2х=3, х=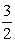
Ответ: х1=-1,5; х2=1,5.
Пример 4. Решить уравнение:½х+2½+3½х½=2½х-1½.
Покажем краткую запись решения уравнения, раскрывая знак модуля «по промежуткам».
Ответ: [-2; 0]
Пример 5. Решить уравнение: (а-1)(а+1)х=(а-1)(а+2), при всех значениях параметра а.
В этом уравнении на самом деле две переменных, но считают х–неизвестным, а а–параметром. Требуется решить уравнение относительно переменной х при любом значении параметра а.
Если а=1, то уравнение имеет вид 0×х=0, этому уравнению удовлетворяет любое число.
Если а=-1, то уравнение имеет вид 0×х=-2, этому уравнению не удовлетворяет ни одно число.
Если а¹1, а¹-1, тогда уравнение имеет единственное решение 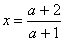
Ответ: если а=1, то х – любое число;
если а=-1, то нет решений;
если а¹±1, то 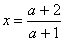
2. Системы уравнений с двумя переменными.
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Решить систему — значит найти все ее решения или доказать, что их нет. Две системы уравнений называются равносильными, если каждое решение первой системы является решением второй системы и каждое решение второй системы является решением первой системы или они обе не имеют решений.
При решении линейных систем используют метод подстановки и метод сложения.
Пример 1. Решить систему уравнений:
Для решения этой системы применим метод подстановки. Выразим из первого уравнения х и подставим это значение 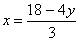
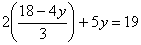
Пример 2. Решить систему уравнений:
Для решения этой системы применим метод сложения уравнений. 8х=16, х=2. Подставим значение х=2 в первое уравнение, получим 10-у=9, у=1.
Пример 3. Решить систему уравнений:
Эта система равносильна одному уравнению 2х+у=5, т.к. второе уравнение получается из первого умножением на 3. Следовательно, ей удовлетворяет любая пара чисел (х; 5-2х). Система имеет бесконечное множество решений.
Ответ: (х; 5-2х), х–любое.
Пример 4. Решить систему уравнений:
Умножим первое уравнение на –2 и сложим со вторым уравнением, получим 0×х+0×у=-6. Этому уравнению не удовлетворяет ни одна пара чисел. Следовательно, эта система не имеет решений.
Ответ: система не имеет решений.
Пример 5. Решить систему:
Из второго уравнения выражаем х=у+2а+1 и подставляем это значение х в первое уравнение системы, получаем 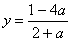
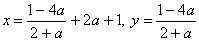
Ответ: при a=-2система не имеет решения,
при а¹-2 система имеет решение 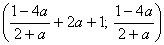
Пример 6. Решить систему уравнений:
Нам дана система из трех уравнений с тремя неизвестными. Применим метод Гаусса, который состоит в том, что равносильными преобразованиями приводят данную систему к треугольной форме. Прибавим к первому уравнению второе, умноженное на –2.
Далее к третьему уравнению системы прибавим второе, умноженное на –3,
наконец прибавим к этому уравнению уравнение у-z=-1, умноженное на 2, получим — 4z=-12, z=3. Итак получаем систему уравнений:
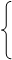
z=3, которая равносильна данной.
Система такого вида называется треугольной.
3. Решение задач с помощью уравнений и систем уравнений.
Покажем на примерах, как можно решать задачи с помощью уравнений и систем уравнений.
Пример 1. Сплав олова и меди массой 32 кг содержит 55% олова. Сколько чистого олова надо добавить в сплав, чтобы в новом сплаве щсодержалось 60% олова?
Решение. Пусть масса олова, добавленная к исходному сплаву, составляет х кг. Тогда сплав массой (32+х)кг будет содержать 60% олова и 40% меди. Исходный сплав содержал 55% олова и 45% меди, т.е. меди в нем было 32·0,45 кг. Так как масса меди в исходном и новом сплавах одна и та же, то получим уравнение 0,45·32=0,4(32+х).
Решив его, находим х=4, т.е. в сплав надо добавить 4 кг олова.
Пример 2. Задумано двузначное число, у которого цифра десятков на 2 меньше цифры единиц. Если это число разделить на сумму его цифр, то в частном получится 4 и в остатке 6. Какое число задумано?
Решение. Пусть цифра единиц есть х, тогда цифра десятков равна х-2 (х2), задуманное число имеет вид 10(х-2)+х=11х-20. Сумма цифр числа х-2+х=2х-2. Следовательно, разделив 11х-20 на 2х-2, получим в частном 4 и в остатке 6. Составляем уравнение: 11х-20=4(2х-2)+6, т.к. делимое равно делителю, умноженному на частное, плюс остаток. Решив это уравнение, получим х=6. Итак, было задумано число 46.
Пример 3. Три ящика наполнены орехами. Во втором ящике на 10% орехов больше, чем в первом, и на 30% больше, чем в третьем. Сколько орехов в каждом ящике, если в первом на 80 орехов больше, чем в третьем?
Решение. Пусть в первом ящике было х орехов, в третьем – y. Тогда во втором ящике было х+0,1х=1,1х или y+0,3y=1,3y. Учитывая, что в первом ящике было на 80 орехов больше, чем в третьем, составляем систему уравнений:
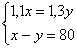
Замечание. Можно эту задачу решить, не составляя системы уравнений. Пусть в первом ящике было х орехов, тогда в третьем — х-80, во втором — 1,1х или 1,3(х-80). Имеем уравнение: 1,1х=1,3(х-80), х=520.
Ответ: в первом ящике было 520 орехов, во втором — 572, в третьем — 440.
Пример 4. Из двух городов А и В, расстояние между которыми 180 км, в 6 ч 20 мин. вышли навстречу друг другу автобус и легковой автомобиль. Их встреча произошла в 7 ч 50 мин. Если бы автобус вышел на 1 ч 15 мин. раньше, а легковой автомобиль на 15 мин. позже, то они встретились бы в 7 ч 35 мин. Какова скорость автобуса и легкового автомобиля?
Решение. Пусть скорость автобуса V1 км/ч, скорость легкового автомобиля V2 км/ч. Так как их встреча произошла через 1,5 ч, то имеем уравнение:1,5V1+1,5V2 =180. Если бы автобус вышел на 1ч 15 мин. раньше, то он был бы в пути 2 ч 30 мин. (7 ч 35 мин. – 5 ч 5 мин.= 2 ч 30 мин.). Если бы легковой автомобиль вышел на 15 мин. позже, то он был бы в пути 1 ч (7 ч 35 мин. – 6 ч 35 мин.= 1ч). Получаем уравнение: 2,5V1 +V2 =180.
Таким образом, имеем систему двух уравнений с двумя неизвестными:
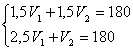
Ответ: 40 км/ч, 80 км/ч.
4. Линейные неравенства с одной переменной.
Если переменной х придать какое-либо числовое значение, то мы получим числовое неравенство, выражающее либо истинное, либо ложное высказывание. Пусть, например, дано неравенство 5х-13х+2. При х=2 получим 5·2-13·2+2 – истинное высказывание (верное числовое высказывание); при х=0 получаем 5·0-13·0+2 – ложное высказывание. Всякое значение переменной, при котором данное неравенство с переменной обращается в верное числовое неравенство, называется решением неравенства. Решить неравенство с переменной – значит найти множество всех его решений.
Два неравенства с одной переменной х называются равносильными, если множества решений этих неравенств совпадают.
Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, более простым, но равносильным данному; полученное неравенство снова заменяем более простым равносильным ему неравенством и т.д.
Такие замены осуществляются на основе следующих утверждений.
Теорема 1. Если какой-либо член неравенства с одной переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 2. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.
Линейным называется неравенство вида ax+b0 (соответственно ax+b
Пример 1. Решить неравенство: 2(х-3)+5(1-х)³3(2х-5).
Раскрыв скобки, получим 2х-6+5-5х³6х-15,
-3х-1³6х-15, -9х³-14, 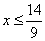
Ответ: 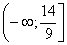
Пример 2. Решить неравенство: 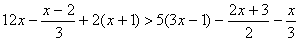
Освободимся от знаменателей, для чего умножим обе части неравенства на положительное число 6, оставив без изменения знак неравенства.
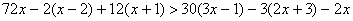
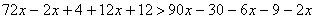
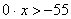
Последнее неравенство верно при любом значении х, так как при любом значении переменной х получается истинное высказывание 0-55. Поэтому множеством его решений служит вся числовая прямая.
Пример 3. Решить неравенство: ½х-1½
На основании определения модуля данное неравенство запишем в виде совокупности двух систем неравенств
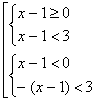
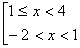
решая эту совокупность получим (2), таким образом решением этого неравенства является промежуток (-2; 4).
Пример 4. Решить неравенство:½х+1½2-х.
отсюда х0,5 из первой системы, а вторая система – не имеет решения.
5. Система и совокупности неравенств.
Говорят, что несколько неравенств с одной переменной образуют систему, если ставится задача найти множество общих решений заданных неравенств.
Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств.
Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих систему. Неравенства, образующие систему, объединяются фигурной скобкой.
Например:
Иногда используется запись в виде двойного неравенства. Например, систему неравенств 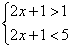
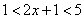
Говорят, что несколько неравенств с одной переменной образуют совокупность, если ставится задача найти множество таких решений, каждое из которых является решением хотя бы одного из этих неравенств.
Значение переменной, при котором хотя бы одно из неравенств, образующих совокупность, обращается в верное числовое неравенство, называется решением совокупности неравенств.
Множество решений совокупности неравенств есть объединение множеств решений неравенств, образующих совокупность. Неравенства, образующие совокупность, иногда объединяются квадратной скобкой. Так, запись 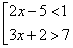
Пример 1. Решить систему неравенств: 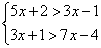
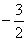
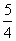
С помощью числовой прямой находим, что пересечением этих множеств служит интервал 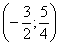
Пример 2. Решить совокупность неравенств:
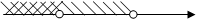
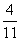
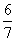
Объединением этих множеств служит промежуток 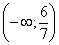
📹 Видео
6 класс, 24 урок, Модульные уравнения и неравенства с одной переменнойСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Как решать неравенства? Часть 1| МатематикаСкачать

6 класс, 31 урок, Системы линейных неравенств с одной переменнойСкачать

Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать

Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать

6 класс, 18 урок, Линейные уравнения с одной переменнойСкачать

Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

ЛИНЕЙНЫЕ НЕРАВЕНСТВА - Как решать линейные неравенства // Подготовка к ЕГЭ по МатематикеСкачать

Урок по теме РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Алгебра 7 Линейное уравнение с одной переменнойСкачать

Решение линейных неравенств с одной переменной, содержащих переменную под знаком модуля. 6 класс.Скачать

Линейные неравенства. Решение линейных неравенств с одной переменной. Числовые промежутки. Алгебра 9Скачать

Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать