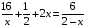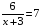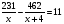Урок дробно рациональные уравнения и неравенства (7 видео)

Урок по теме «Дробно-рациональные уравнения»

Разработка открытого урока по теме «Дробно-рациональные уравнения». Урок повторения и обобщения пройденного материала. Включает в себя задания из заданий ОГЭ.

Содержание

Просмотр содержимого документа «Урок по теме «Дробно-рациональные уравнения»»
Дробно – рациональные уравнения план-конспект урока по математике на тему
Скачать:
Предварительный просмотр:
Конспект урока «Дробные рациональные уравнения»
📹 Видео

Просмотр содержимого документа
«Урок по теме «Дробно-рациональные уравнения»»

ТЕМА УРОКА: Дробно- рациональные уравнение.

Тип урока: Закрепление изученного материала и коррекция знаний.

1.Образовательные цели урока:

— Повторение ранее изученного материала.

— Формирование умения решать дробно-рациональные уравнения, используя при этом различные приемы и методы.

— Самопроверка уровня усвоения темы.

2.Развивающие цели урока:

— Реализация принципов связи теории и практики.

— Развитие памяти, речи, любознательности, познавательного интереса

— Развитие аргументированной речи, доказательного воспроизведения в процессе деятельности.

— Развитие вычислительных навыков.

— Развитие коммуникативных навыков общения и умения слушать и слышать.

3.Воспитательные цели урока.

— Воспитание аккуратности, дисциплины.

— Воспитание настойчивости в достижении цели.

— Воспитание ответственного отношения к учёбе

— Воспитание рациональной организации бюджета времени.

Организационный момент (1-2 мин)

Проверка готовности учащихся к уроку, проверка присутствующих, общий настрой на урок.

Сегодня на уроке мне хотелось бы вас пригласить поглубже заглянуть в замечательный мир математики – в мир уравнений, в мир поиска, в мир исследований.

2. Актуализация знаний, умений, навыков ( 4 мин)

Учитель: Посмотрите на доску. Какие виды уравнений вы видите?

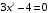
Ученики: Целые и дробно-рациональные.

учитель : Как вы считаете, какое уравнение является « третьим лишним»?

ученик: Первое уравнение, т.к. оно – целое

Сформулируйте тему сегодняшнего урока .Тема : Решение дробных рациональных уравнений.

Откройте тетрадь, запишите число и тему сегодняшнего урока.

Целью урока является: Отработать навыки решения дробно-рациональных уравнений, которые встречаются в ОГЭ.

Великий физик, учёный, Нобелевский лауреат, автор «Теории относительности» говорил: «Мне приходится делить своё время между политикой и уравнениями… Уравнения для меня важнее, потому что политика – для настоящего, а уравнения – для вечности».

Сегодня на уроке мы вспомним теоретический материал по данной теме и решим несколько уравнений, используя различные методы и приемы.

Актуализация знаний, умений, навыков (5 мин)

1. Повторение теоретического материала по данной теме.

— Какие виды уравнений вы знаете? (Целые, рациональные, линейные, квадратные, дробно-рациональные.)

(На доске) ; ; ; ;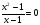

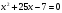
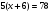
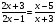
— Какие уравнения называются дробными рациональными? (Уравнения называются дробными рациональными, если его обе части являются рациональными выражениями, причём хотя бы одно из них дробное выражение (содержит деление на переменную))

— Какие вам известны способы решения дробных уравнений?

(заранее на доске)

Классификация способов решения

дробных рациональных уравнений

Условие равенства дроби нулю

Умножение обеих частей уравнения на знаменатель

Применение основного свойства пропорции

Метод введения новой переменной

— Объясните, как решают дробно-рациональные уравнения? Каков алгоритм решения?

(заранее на доске)

Находят общий знаменатель дробей, входящих в уравнение;

Умножают обе части уравнения на этот знаменатель;

Решают получившееся целое уравнение;

Исключают из его корней те, которые обращают в нуль общий знаменатель дробей.

Отработка и закрепление полученных навыков

Индивидуальная работа (10 мин)

— Назовите вид уравнения, определите, каким методом может быть решено каждое из данных целых уравнений, найдите корни уравнений.

( при решении двух уравнений ученики работают по одному на доске, остальные в тетради)

3)Решите задачу: (ОГЭ №22)

Теплоход прошёл 108 км по течению реки и 84 км против течения, затратив на весь путь 8ч. Найдите собственную скорость теплохода, если скорость течения реки 3 км/ч.

Пусть х км/ч собственная скорость теплохода. Заполним таблицу

Видео:Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

Дробно – рациональные уравнения
план-конспект урока по математике на тему

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Скачать:

Вложение	Размер
razrabotka_uroka.doc	407 КБ

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Предварительный просмотр:

Тема урока: «Дробно – рациональные уравнения»

Цели: 1. Систематизировать, обобщить знания и умения учащихся по применению методов решения уравнений;

2. способствовать формированию умений применять приёмы сравнения, обобщения, выделения главного; развивать творческие способности учащихся путём решения усложнённых уравнений;

3. побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.

Оборудование: оценочные листы у учащихся, отпечатанные тесты, таблицы с уравнениями, таблица «Способы решений квадратных уравнений».

І.1). Сообщение темы занятия и целей.

2). Устные упражнения: а). Чтобы решать уравнения, нужно совершать ряд преобразований, и делать это следует очень осмотрительно. Решая уравнения, ученик рассуждал так:

Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Конспект урока «Дробные рациональные уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Урок алгебры в 9 классе.

Дробные рациональные уравнения. (первый урок).

Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова. Учебник для 9 класса общеобразовательных учреждений .

РЕШЕНИЕ ДРОБНО-РАЦИОНАЛЬНЫХ УРАВНЕНИЙ

формирование понятия дробно- рационального уравнения;

рассмотреть различные способы решения дробных рациональных уравнений;

рассмотреть алгоритм решения дробных рациональных уравнений.

обучить решению дробных рациональных уравнений по алгоритму;

проверка уровня усвоения темы путем проведения тестовой работы.

развитие умения правильно оперировать полученными знаниями, логически мыслить;

развитие интеллектуальных умений и мыслительных операций — анализ, синтез, сравнение и обобщение;

развитие инициативы, умения принимать решения, не останавливаться на достигнутом;

воспитание познавательного интереса к предмету;

воспитание самостоятельности при решении учебных задач;

воспитание воли и упорства для достижения конечных результатов.

Тип урока: урок – объяснение нового материала.

1. Организационный момент.

Здравствуйте, ребята! На доске написаны уравнения посмотрите на них внимательно. Все ли из этих уравнений мы умеем решать? Какие нет и почему?

Как называются выражения из которых составлены 5,6, 7 и 8 уравнения? (дробно-рациональными)

Уравнения, в которых левая и правая части, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Попробуйте сформулировать тему нашего урока. Итак, открываем тетради и записываем тему урока «Решение дробных рациональных уравнений».

Давайте сформулируем цели нашего урока (дети самостоятельно формулируют цели урока)

А сейчас мы повторим основной теоретический материл, который понадобиться нам для изучения новой темы. Ответьте, пожалуйста, на следующие вопросы:

Что такое уравнение? (Равенство с переменной или переменными.)

— Как называется уравнение №1? (Линейное.) Способ решения линейных уравнений. (Все с неизвестным перенести в левую часть уравнения, все числа — в правую. Привести подобные слагаемые. Найти неизвестный множитель).

— Как называется уравнение №3? (Квадратное.) Способы решения квадратных уравнений. (По формулам, используя теорему Виета и ее следствия.)

— Какие свойства используются при решении уравнений? (1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному. 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.)

3. Объяснение нового материала.

Итак, мы уже знаем правила решения дробных рациональных уравнений. Что же это за правила? Попробуйте мне их сформулировать:

1группа будет искать решение, применяя свойство пропорции. Что такое пропорция? (Равенство двух отношений.) Сформулируйте основное свойство пропорции. (Если пропорция верна, то произведение ее крайних членов равно произведению средних членов.)

Карточка 1: РЕШИТЬ ДРОБНОЕ РАЦИОНАЛЬНОЕ УРАВНЕНИЕ,

ИСПОЛЬЗУЯ СВОЙСТВО ПРОПОРЦИИ

Произведение средних членов равно произведению

крайних членов пропорции.

2группа — применяя свойство равенства дроби нулю. Ответьте когда дробь равна нулю? (Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.)

Карточка 2: РЕШИТЬ ДРОБНОЕ РАЦИОНАЛЬНОЕ УРАВНЕНИЕ,

УМНОЖЕНИЕМ НА ОБЩИЙ ЗНАМЕНАТЕЛЬ

Обе части уравнения можно умножить или разделить

на одно и то же отличное от нуля число.

3группа решает методом умножения на общий, не равный нулю знаменатель.

Карточка 3: РЕШИТЬ ДРОБНОЕ РАЦИОНАЛЬНОЕ УРАВНЕНИЕ,

УМНОЖЕНИЕМ НА ОБЩИЙ ЗНАМЕНАТЕЛЬ

Обе части уравнения можно умножить или разделить

на одно и то же отличное от нуля число.

После решения и обсуждения в группах один представитель от каждой группы выходит к доске и записывает решение уравнения на доске.

х=0 или х=6 2х²(х-6)=0

Ответ: х=0, х=6 х=0, х=6 х²-6х=0 х=0, х=6

Ответ: х=0, х=6 4х≠ 0 х ≠0

Если получились разные ответы, то задаю наводящие вопросы:

Сравниваем ответы. Объясните, почему так получилось? Почему в одном случае два корня, в другом – один? Какие же числа являются корнями данного дробно-рационального уравнения?

Чем отличаются уравнения № 2 и 4 от уравнений № 5,6,7,8? (В уравнениях № 2 и 4 в знаменателе числа, № 5-8 – выражения с переменной.)

Что такое корень уравнения? (Значение переменной, при котором уравнение обращается в верное равенство.)

Как выяснить является ли число корнем уравнения? (Сделать проверку.)

При выполнении проверки некоторые ученики замечают, что приходится делить на нуль. Они делают вывод, что число 0 не является корнем данного уравнения.

Возникает вопрос: что же необходимо добавить в каждый из этих способов, чтобы исключить данную ошибку? ( исключить посторонние корни) —— дописываем на доске неравенство знаменателя нулю или ОДЗ).

Здесь мы столкнулись с понятием постороннего корня, т. е. это значение переменной, которое не входит в область определения дробно-рационального выражения.

Давайте попробуем сформулировать алгоритм решения дробных рациональных уравнений данными способами. Рассмотрим первый способ: равенство дроби нулю. Дети сами формулируют алгоритм

1. Алгоритм решения дробных рациональных уравнений:

Перенести все в левую часть.

Привести дроби к общему знаменателю.

Составить систему: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.

Проверить неравенство, чтобы исключить посторонние корни.

Как оформить решение, если используется основное свойство пропорции?

Алгоритм решения дробных рациональных уравнений.

1. Воспользоваться свойством пропорции: в верной пропорции произведение крайних

членов равно произведению средних.

2. Решить полученное целое уравнение.

3. Исключить из корней те, которые обращают в нуль общий знаменатель.

4. Записать ответ.

Как оформить решение, если используется умножение обеих частей уравнения на общий знаменатель?

3. Алгоритм решения дробных рациональных уравнений:

Найти общий знаменатель дробей, входящих в уравнение.

Умножить обе части уравнения на общий знаменатель, не равный нулю.

Решить получившееся целое уравнение.

Исключить из корней те, которые обращают в нуль общий знаменатель. 5. Записать ответ.

Назовите у каждого уравнения ОДЗ. Мы с вами рассмотрели три способа решения дробных рациональных уравнений.

4. Первичное осмысление нового материала.

А теперь каждой группе я предлагаю решить уравнения из предложенных любым из способов.

Карточки для групп: Решите уравнения:

(Работа в группах. Учащиеся выбирают способ решения уравнения самостоятельно в зависимости от вида уравнения). Учитель контролирует выполнение задания, отвечает на возникшие вопросы, оказывает помощь ученикам. Самопроверка: ответы записаны на доске

в) Ответ: х = -3, х =2

г) -5 – посторонний корень. Ответ: х = 5;

5. Подведение итогов урока.

Итак, сегодня на уроке мы с вами познакомились с дробными рациональными уравнениями, научились решать эти уравнения различными способами, проверили свои знания с помощью самостоятельной работы. Какой метод решения дробных рациональных уравнений, по Вашему мнению, является более легким, доступным, рациональным? Но, независимо от метода решения дробных рациональных уравнений, о чем необходимо не забывать? В чем «коварство» дробных рациональных уравнений?