Урок биквадратные уравнения 8 класс мерзляк

Видео:Биквадратные уравнения. 8 класс алгебра.Скачать

План-конспект урока: Уравнения, сводящиеся к квадратным.

«Уравнение представляет собой наиболее серьезную

и важную вещь в математике».

Просмотр содержимого документа
«План-конспект урока: Уравнения, сводящиеся к квадратным.»

Учитель: Татарникова Наталья Николаевна.

Тема: Уравнения, сводящиеся к квадратным.

Тип урока: Урок изучение новых знаний.

Цель урока: Образовательные:

Познакомить учащихся с понятием «биквадратное уравнение»;

Рассмотреть способ решения биквадратных уравнений;

Способствовать формированию у учащихся умения решать биквадратные уравнения, методом замены переменных;

Отработать навыки решения квадратных уравнений.

Способствовать формированию навыков общения, умения работать в коллективе;

Способствовать формированию самостоятельности, аккуратности, правильной речи, взаимопомощи, точности.

Способствовать развитию умения учащихся анализировать, делать выводы, планировать и оценивать свои действия.

Учебник Алгебра, 8 класс, А. Г. Мерзляк, В. Б. Полонский, М. С. Якир, учебник для учащихся общеобразовательных организаций;

Методическое пособие: Е. В. Буцко, А. Г. Мерзляк, В. Б. Полонский, М. С. Якир, алгебра 8 класс;

Дидактический материал: А. Г. Мерзляк, В. Б. Полонский, Е. М. Рабинович, М. С. Якир, алгебра, 8 класс.

Планируемые результаты: Учащиеся научатся решать биквадратные уравнения, решать уравнения методом замены переменных.

Форма работы: индивидуальная, фронтальная, групповая.

Оборудование: доска, мел, раздаточный материал, компьютер, проектор.

Проверка домашнего задания;

Актуализация знаний, постановка проблемы;

Изучение нового материала;

Физминутка для глаз;

Первичное закрепление изученного материала;

Рефлексия. Постановка домашнего задания.

Основные понятия: Биквадратное уравнение, метод замены переменных.

Общие сведения: По программе на данную тему запланировано 4 часа, номер урока по КТП 83.

Организационный момент: (1 мин) Мотивация.

Цель: создать благоприятный психологический и эмоциональный настрой на работу и возникновение у ученика осознанного включения в учебный процесс.

Здравствуйте, ребята! Сегодня на уроке мы постараемся узнать еще больше об уравнениях. Эпиграф нашего урока- слова английского физика Оливера Лоджа:

«Уравнение представляет собой наиболее серьезную

и важную вещь в математике».

Вы будете исследователями, будете работать в группах. Желаю вам удачи, хорошего настроения и взаимопонимания!

Проверка домашнего задания (2 мин).

На экране ответы на все уравнения. Учащиеся проверяют свою работу (слайд 1). Давайте подведем итог. Кто справился со всеми уравнениями? Кто выполнил половину? Кто не справился?

Актуализация знаний. Постановка проблемы (10 мин).

Цель: Актуализировать умение решать квадратные уравнения и неполные квадратные уравнения.

Вначале выполним устные упражнения (слайд 2).

Решить уравнение х 2 = 81, а 2 = 16, у 2 = 1, в 2 = 0, с 2 = 23, р 2 = — 25, к 2 = — 16, х 2 = .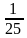

Что записано на доске? (уравнения) (слайд3)

6 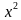– х = 0 Как называется это уравнение? (неполное квадратное уравнение. Как оно решается (вынесением общего множителя).

х 2 + 6х — 7 = 0 Как называются эти уравнения (приведенное квадратное уравнение)

х 2 – 8х + 15 = 0 способ решения (по теореме Виета). Сформулируйте теорему.

Математический тест. (карточки) (слайд 3)

1.Найдите коэффициенты уравнения 4х 2 + х – 1 = 0.

а) а = 4; в = -1; с = -1 б) а = 4; в = 1; с = -1 в) а = 1; в = 4; с = -1

2. Решите уравнение: х 2 — 5х +4 = 0.

а) 4; 5; б) -4; 5; в) 4; -5.

3. Квадратное уравнение не имеет решения, если:

4. Не решая уравнение 7х 2 +11х -18 = 0, найдите его корни

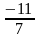
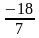
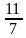
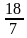
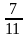
а) ; б) ; в) ; 18.

Учащиеся выбирают свои варианты ответов в процессе обсуждения в группе и проверяют их.

При исправлении ошибок некоторые учащиеся пришли к выводу, что им необходимо повторить формулы корней квадратных уравнений. (слайд 4)

Учащимся даются карточки с заданиями.

х 2 – 64 = 0 2) х 2 – х = 0 3) 3х 2 – 5х – 2 =0 4) 2х 4 – 5х 2 + 7 = 0

х 2 =64 х(х-1)=0 D=25+24=49

х_1,2= ±8 х=0 или х=1 х₁= 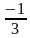х₂=2

В ходе обсуждения учащиеся приходят к выводу, что они не знают, как решается последнее уравнение. Учащиеся ставят проблему: Как решить данное уравнение и как оно называется.

Уравнение х 4 – 9х 2 + 20 = 0 называется: (слайд 5)

а) линейной б) квадратной в)биквадратное г) приведенное квадратное .

В ходе обсуждения учащиеся делают вывод, что уравнение называется биквадратным.

А что означаетприставка «би»? Этот вопрос был задан на предыдущем уроке в качестве творческого задания.

Би…- часть сложных слов, обозначающая: состоящий из двух частей, имеющий два признака, взятый дважды (бицепс).

Учащиеся формулируют тему урока, записывают «Решение уравнений, сводящихся к квадратным» (слайд 6).

Изучение нового материала (8 мин).

Цель: Способствовать умению самостоятельно добывать знания §23 стр. 187. Учащиеся читают определение, выводят алгоритм решения биквадратных уравнений и записывают его:

Ввести новую переменную t = х 2 .

Решить получившееся квадратное уравнение.

С учетом замены решить следующие уравнения.

Возвращаемся к проблемным уравнениям.

2х 4 – 5х 2 + 7 = 0 2) х 4 – 9х 2 + 20 = 0

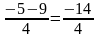
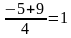
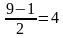
t₁= t₂= t₁= t₂=

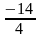
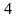
х₁ 2 = х₂ 2 =1 х₁ 2 = х₂ 2 =5

Ø х₁=-1 х₂=1 х₁=-2 х₂=2 х₃= 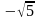х₄=

Ответ: х₁=-1 х₂=1 Ответ: х₁=-2 х₂=2 х₃= 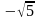х₄=

Физминутка для глаз. Включает различные упражнения для снятия напряжения и утомления глаз (1 мин).

Первичное закрепление изученного материала (10 мин)

Решение биквадратных уравнений №775 (нечет), 779 (нечет 1 столбик). Двое учащихся работают у доски, комментируя решение, остальные работают в тетрадях.

Самостоятельная работа (10 мин).

Цель: Проверить умения применять полученные знания.

Сейчас каждый проверит сам себя – насколько он усвоил способы решения биквадратных уравнений и научился их применять. Когда вы закончите работу над частью «А» — «поднимите руку». Получите ключ для выполнения самопроверки к этой части. Если задание «А» выполнено правильно, получаете следующее задание и т.д.

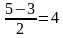
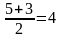
Ø t₁= t₂= t₁= -9 t₂=9

х₁ 2 = 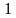х₂ 2 =5 Ø y 2 =9

х₁=-1 х₂=1 х₃= 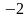х₄=2 y₁=-3 y₂=3

Б.1) Решить уравнение: № 164 (3) стр. 27 (дидактический материал) 4x 4 — 13x 2 +3=0;

t₁= 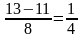t₂=

2)Решить уравнение, не используя алгоритм:

В. Решить уравнение

После выполнения работы учащиеся в группах обсуждают решения, исправляют допущенные ошибки.

Рефлексия. Постановка домашнего задания.

Цель: Формирование самостоятельности в учебно-познавательной деятельности, осознание учащимися своей учебной деятельности.

Учащиеся записывают домашнее задание: § 23, № 776 (нечет), 778 (1,3,5), 780 (1).

Какой новый вид уравнения мы узнали? К какому уравнению приводится биквадратное уравнение? Оцените свою работу на уроке, заполните лист самооценки.

Лист самооценки и взаимооценки в работе группы

Критерий (за каждый критерий от 0 до 5 баллов)

Я внес(ла) большой вклад в работу группы

Я умею выслушивать мнение других ребят, принимать другую точку зрения

Я умею объяснять свою точку зрения, приводить доводы и убеждать

Я готов(а) принимать новые идеи, отличающиеся от моего первоначального мнения

Тема: Уравнения, сводящиеся к квадратным.

Класс состоит из учащихся различного уровня подготовки и математических способностей, поэтому на уроке осуществлялся дифференцированный и проблемный подходы.

Перед уроком была поставлена триединая дидактическая цель урока, которая реализовывалась через следующие аспекты:

Отработка способов решения уравнений, сводящихся к квадратным по алгоритму;

Формирование навыков решения уравнений, сводящихся к квадратным по алгоритму.

Развивать умение выявлять закономерности, абстрагировать и обобщать;

развивать навыки самоконтроля и взаимоконтроля.

воспитание трудолюбия, взаимопомощи, математической культуры.

Поставлены реальные цели образовательного, развивающего и воспитательного аспектов. Цели данного урока соответствуют стандартным требованиям программы и связаны с предыдущими занятиями.

Структура урока: комбинированный урок, сочетает различные виды деятельности, с элементами проблемного обучения.

Форма организации деятельности учащихся: фронтальная, групповая, индивидуальная.

Оборудование: доска, мел, раздаточный материал, компьютер, проектор.

Структура урока соответствует типу урока и его дидактическим задачам. На уроке были использованы следующие методы обучения:

словесные (беседа с учащимися);

наглядные (демонстрация презентации);

Были использованы следующие формы познавательной деятельности: фронтальная, индивидуальная, групповая, которые в ходе урока сменяли друг друга.

Время, отведенное на все этапы урока, было распределено рационально. Поддерживался средний темп работы учащихся.

Урок начинался с организационного момента, задача которого подготовить учащихся к работе на уроке. Этот этап включал в себя мотивацию учащихся, хотя и был непродолжительным, позволил быстро включить учащихся в ход урока, активировать внимание.

Следующий этап – проверка домашнего задания. Задача данного этапа выявление уровня усвоения пройденного материала.

За ним шел этап актуализации знаний. Задача данного этапа выявление пробелов в знаниях учащихся и их устранение. С этой целью использовалась устная фронтальная работа. Обязательны были на этапе, повторение теоретического материала, комментирование ответов учащихся, постановка проблемы, повторение формул нахождения корней квадратного уравнения.

Следующий этап – изучение нового материала. Дети с помощью учителя решали биквадратные уравнения, методом замены пременных.

Затем ребята работали самостоятельно с карточками. Был осуществлен дифференцированный подход к заданиям. После выполнения самостоятельной работы дети в группе обсуждали решения.

Завершающим этапом была рефлексия: оценка учащимися и учителем результатов урока, подведение итогов, постановка домашнего задания.

Между всеми этапами четко прослеживается логическая связь и завершенность каждого этапа. В ходе урока была достигнута триединая дидактическая цель. Учащиеся повторили формулы нахождения корней квадратного уравнения, закрепили умения решать квадратные уравнения. Учащиеся учились рассуждать, логично излагать свои мысли, работать в группе.

Выбранные формы и методы обучения способствовали созданию на уроке положительной психологической атмосферы.

Общение учащихся и учителя доброжелательное, доверительное.

По моему мнению, реализованы все поставленные дидактические цели и задачи урока. Учитель и учащиеся получили удовольствие от общения. Ребята участвовали в подведении итогов урока. Отметки за урок выставлены и прокомментированы.

Видео:Решение уравнений сводящихся к квадратным уравнениям. Биквадратные уравнения – 8 класс алгебраСкачать

Презентация «Биквадратные уравнения» 8 класс УМК А.Г. Мерзляк

Код для использования на сайте:

Скопируйте этот код и вставьте себе на сайт

Для скачивания поделитесь материалом в соцсетях

После того как вы поделитесь материалом внизу появится ссылка для скачивания.

Подписи к слайдам:

УМК: А.Г. Мерзляк и др.

Определение Биквадратным уравнением называется уравнение вида а + в + с = 0 где х – переменная, а, в и с – некоторые числа, причём а≠0. Решение биквадратных уравнений Биквадратные уравнения решают с помощью введения дополнительной переменной Алгоритм решения Например: решить уравнение -5х²-36 = 0 Пусть х² = t, тогда t² — 5t – 36 = 0 АЛГОРИТМ 1).Приводят уравнение к стандартному виду 2). Вводят дополнительную (новую) переменную t² — 5t – 36 = 0 т.к. это приведённое квадратное уравнение, то по т. Виета имеем: = 9 = — 4 3). Составить квадратное уравнение с новой переменной () 4). Решить новое квадратное уравнение с переменной Сделаем обратный переход к переменной х Сделаем обратный переход к переменной х (у нас х² = ): 1) если = 9, то х² = 9 => х= ± 3 2) если = — 4, то х² = — 4 => нет решения 5). Вернуться к замене переменной (сделать обратный переход от переменной t к переменной x) и решить полученные квадратные уравнения Данное биквадратное уравнение имеет 2 решения. Данное биквадратное уравнение имеет 2 решения. Ответ: ± 3 6). Сделать вывод о числе решений уравнения 7). Записать ответ Решите уравнения (самостоятельно)

Работа по учебнику

стр. 188 № 775; 776

• http://www.bottomlinecoaching.ca/wp-content/uploads/2013/01/30-percent-QM.jpg
• http://www.devpractices.ru/wp-content/uploads/2013/04/stockfresh_1802021_3d-white-people-lying-on-a-question-mark_sizeS_f967ef-370×330.jpg
• http://dom-pravo.ru/wp-content/uploads/2013/10/%D0%9E%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5-%D0%B7%D0%B5%D0%BC%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D1%85-%D1%83%D1%87%D0%B0%D1%81%D1%82%D0%BA%D0%BE%D0%B2.jpg
• http://berichnow.ru/wp-content/uploads/2014/01/trebovaniya-ryinka-k-tovaru.png
• Алгоритм/https://cloud.prezentacii.org/19/05/144557/images/screen8.jpg
• Примеры/https://doc4web.ru/uploads/files/67/67304/hello_html_20926b3.gif
• А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Алгебра: 8класс: учебник для учащихся общеобразовательных организаций, – М.: Вентана-Граф, 2018
• А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир.: Алгебра : 8 класс: дидактический материал: пособие для учащихся общеобразовательных организаций / – М.: Вентана-Граф, 2016

Автор шаблона презентации:

Наталья Николаевна Коломина учитель математики МКОУ «Хотьковская СОШ»

Думиничского района Калужской области.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Технологическая карта урока по теме Решение уравнений, сводящимся к квадратным уравнениям

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Алгебра 8 класс : учебник для учащихся общеобразовательных организаций /

А.Г.Мерзляк, В.Б.Полонский, М.С.Якир

ФИО учителя, школа

Смирнова Татьяна Александровна, МОУ Ново-Харитоновская СОШ №10 с УИОП

Решение уравнений, сводящимся к квадратным уравнениям.

Урок общеметодологической направленности

Презентация, карточки с заданиями

Этапы учебного занятия

УУД, формирующиеся на данном этапе

Содержание, дидактический материал

1. Организовать актуализацию требований к учащимся со стороны учебной деятельности.

2. Создать условия для возникновения внутренней потребности, включения в учебную деятельность.

— смыслообразование (Я должен посмотреть…)

— планирование учебного сотрудничества с преподавателем и со сверстниками.

Сегодня на уроке мне хотелось бы вас пригласить «поглубже» заглянуть в замечательный мир математики – в мир уравнений, в мир поиска и исследований.

2. Проверка домашнего задания. Подготовка к работе на основном этапе.

1. Организовать актуализацию изученных способов действий, достаточных для построения новых знаний.

2. Зафиксировать актуализированные способы действия в речи (повторение правил).

3. Зафиксировать актуальные способы действия в знаках (эталоны, схемы, опора по правилам).

4. Организовать обобщение актуализир. способов действий. Мотивировать учащихся к учебному действию.

5. Организовать выполнение учащимися учебного действия.

6. Зафиксировать учебные затруднения (групповое или индивидуальное)

— общеучебные умения структурировать знания, контроль и оценка процесса и результатов деятельности.

— анализ, сравнение, синтез.

— контроль и оценка прогнозирования (при анализе учебного действия).

Но для начала давайте вспомним:

Какое уравнение называется квадратным?

Какие квадратные уравнения называются неполными?

Приведите примеры неполных квадратных уравнений.

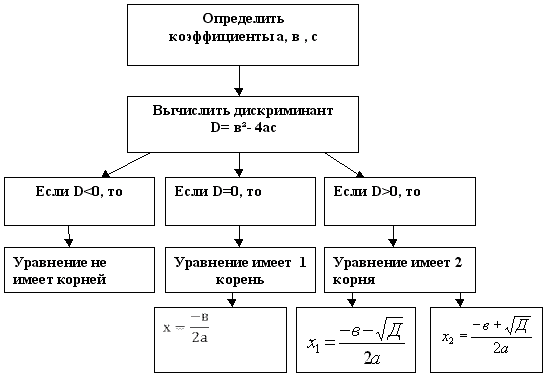
Сформулируйте определение дискриминанта квадратного уравнения.

Сколько корней может иметь квадратное уравнение?

Напишите основную формулу корней квадратного уравнения.

Сформулируйте теорему Виета, обратную теорему.

Какое уравнение называется биквадратным?

Все способы решений, известных вам уравнений, можно образно представить в виде “ключей”.

Символ урока – связка ключей — «Квадратные уравнения», «Дробно-рациональные уравнения», «Уравнения, сводящиеся к квадратным».

Определите вид каждого уравнения и найдите корни (№ 1 — № 5), где это возможно выполнить (устно).

2) (ответ: t1 = 1, t2 = 4)

3. Усвоение новых знаний и способов действия

Организовать построение проекта изучения нового знания:

1. учащиеся ставят цель проекта (что является целью — тема).

2. учащиеся определяют средства (алгоритмы, модели, справочники, Интернет. )

3. учащиеся формулируют шаги, которые необходимо сделать для реализации поставленной цели.

— целеполагание как постановка учебной задачи,

— умение структурировать знания, постановка и формулировка проблемы, умение осознанно и произвольно строить речевые высказывания.

выбор наиболее эффективных способов решения задач.

Но в нашей связке есть ещё один «ключик», который вам ещё не известен — «Уравнения, сводящиеся к квадратным».

И наша задача состоит в том, чтобы «отточить» этот ключик и научиться, таким ключом, открывать тайну уравнений.

Поэтому, тема нашего урока: «Уравнения, сводящиеся к квадратным».

Давайте рассмотрим уравнение (№ 6).

— Какую особенность в данном уравнении Вы заметили? — Выражение обозначим буквой t. Что изменилось в уравнении? (получилось квадратное уравнение относительно t). И такой подход к решению уравнений называют – методом введения новой переменной, который позволяет свести данное уравнение к квадратному.

Введем замену: Пусть х-1 = t, тогда исходное уравнение примет вид – по т. Виета найдём корни уравнения: t1 = 1, t2 = 4. Но нам нужны значения х. Вернемся к подстановке: х-1 = t ,получим линейные уравнения:

Давайте ещё раз проанализируем решение данного уравнения, каких целей добились.

План исследования уравнения:

Провести анализ уравнения.

Составить план решения.

Реализовать план решения.

Составить анализ метода решения и систематизировать опыт.

4 пункт плана исследования уравнения — составление анализа метода решения — это ещё один этап нашей исследовательской работы.

Знаете ли вы, что английский математик Джеймс Джозеф Сильвестр называл музыку математикой чувств, а математику – музыкой разума.

Продолжим нашу работу.

Рассмотрим следующее уравнение (№ 7).

Раскроем скобки, объединяя 1 – 4 множители и 2 – 3 множители. Получим уравнение Нетрудно заметить, что если решать уравнение, раскрывая скобки дальше, то в левой части уравнения получится многочлен четвёртой степени – сложно.

Введем замену: Пусть ,тогда исходное уравнение примет вид:

Вернемся к подстановке, получим уравнения:

Подведём итог нашей исследовательской работы.

Вывод: Итак, два различных уравнения мы решили одним и тем же методом – методом введения новой переменной, где первоначальное уравнение приводится к квадратному.

4. Реализация построенного проекта и закрепление изученных способов действий.

1. Организовать реализацию построенного проекта в соответствии с планом.

2. Организовать фиксацию нового способа действия в речи.

3. Организовать фиксацию нового действия в знаках.

4. Обсуждение возможности применения нового способа действий для решения всех заданий данного типа.

5. Организовать усвоение учащимися нового способа действий во внешней речи

( в парах или группах, фронтально)

Планирование учебного сотрудничества

— поиск и выделение необходимой информации

— построение логической цепи рассуждения

Решение заданий из учебника.

5. Контроль и самооценка знаний и способов действия

1. Организовать самостоятельное выполнение учащимися типовых заданий на новый способ действия.

2. Организовать сопоставление работы с эталоном для самопроверки.

3. По результатам выполнения самостоятельной организовать рефлексию деятельности по применению нового способа деятельности.

а) контроль и коррекция в форме сравнения способа действия и его результата с заданным эталоном;

б) планирование – определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий.

-умение осознанно и произвольно строить высказывания (устно/письменно)

Выполнение заданий самостоятельно (слайд 3-4)

а) Какую подстановку можно выполнить в каждом уравнении?

б) А теперь попробуйте свести данное уравнение к квадратному, подстановку мы уже определили (выберите по желанию для себя любое уравнение) и проверим.

Самопроверка с использованием документ камеры или слайдов презентации.

Анализ затруднений при выполнении заданий.

6. Коррекция знаний и способов действий

1. Организовать выявление типов заданий, где используется новый способ действия.

2. Организовать повторение учебного содержания необходимого для обеспечения содержательной непрерывности.

7. Подведение итогов занятия, информация о домашнем задании.

1. Организовать фиксацию нового содержания изученного на уроке.

2. Организовать фиксацию неразрешенных затруднений на уроке как направлений будущей учебной деятельности.

3. Организовать обсуждение и запись домашнего задания.

— умение структурировать знания

— оценка процессов и результатов деятельности

— осознание того, что уже усвоено и что ещё подлежит усвоению

Сегодня на уроке мы только попробовали подобрать наш «ключик» к решению уравнений. Вам предстоит ещё большая работа, чтобы этот ключ работал в совершенстве. Благодарю вас за урок. Желаю удачи вам, новых поисков и открытий.

§23 (пример 2), №780, 795(1,2)

1. Организовать рефлексию учащихся по поводу своего психоэмоционального состояния, мотивации, своей деятельности, взаимодействия с преподавателем и одногруппниками.

— умение выражать свои мысли

— оценивание качества своей и общей учебной деятельности

Учащиеся заполняют листы самооценки.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 949 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Биквадратное уравнениеСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 569 258 материалов в базе

Другие материалы

• 23.10.2020
• 75
• 2

• 23.10.2020
• 126
• 8

• 23.10.2020
• 1203
• 23

• 23.10.2020
• 110
• 1

• 23.10.2020
• 174
• 7

• 23.10.2020
• 65
• 0

• 23.10.2020
• 80
• 2

• 23.10.2020
• 67
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 23.10.2020 231
• DOCX 68.2 кбайт
• 40 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Колобова Вероника Львовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 1 год и 3 месяца
• Подписчики: 0
• Всего просмотров: 9125
• Всего материалов: 68

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Уравнения, сводящиеся к квадратным. Биквадратное уравнениеСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

В России могут объявить Десятилетие науки и технологий

Время чтения: 1 минута

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🎬 Видео

Решение биквадратных уравнений. Практическая часть. 1ч. 8 класс.Скачать

Дробно-рациональные уравнения. 8 класс.Скачать

5 Лайфхаков Которые Помогут Решить Биквадратное УравнениеСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Решение биквадратных уравнений. Практическая часть. 2ч. 8 класс.Скачать

БИКВАДРАТНОЕ УРАВНЕНИЕ класс математикаСкачать

Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

Алгебра 8 класс (Урок№27 - Квадратные уравнения. Неполные квадратные уравнения.)Скачать

Биквадратное уравнениеСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Урок алгебры для 8 класса. Тема: "Биквадратные уравнения"Скачать

Теорема Виета. 8 класс.Скачать

Решение уравнений, сводящихся к квадратным уравнениям биквадратное уравнение (урок 1)Скачать