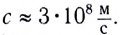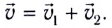Равномерное движение – это движение с постоянной скоростью, то есть когда скорость тела не изменяется ни по модулю, ни по направлению. 

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.
Равномерным прямолинейным движением называется движение, при котором за любые равные промежутки времени тело совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена так же, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости.
Пройденный путь при прямолинейном движении равен модулю перемещения. Чтобы найти путь, пройденный при равномерном движении, надо скорость тела умножить на время движения:
Для описания движения введём прямоугольную систему координат ХОУ. Тогда положение тела определяется его координатами Х и У.
Координаты тела определяются по формуле:
где х0 ; у0 – начальные координаты тела; υх , υу — проекции вектора скорости на оси координат
Значение х0 и у0, а также знаки перед слагаемыми в правых частях уравнений зависят от выбора начала координат и направления осей ОХ и ОУ. Если положительное направление оси ОХ совпадает с направлением движения (с направлением скорости), то проекция скорости на ось ОХ равна величине скорости и положительна. Если положительное направление оси ОХ противоположно направлению движения тела – скорость отрицательна.
Проекция перемещение на ось ОХ равна:
График зависимости перемещения от времени показан на рис.1.5. Из графика видно, что проекция скорости равна
где α- угол наклона графика к оси времени.
Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время).
Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:
Зависимость координаты от времени показана на рис. 1.6. Из рисунка видно, что
следовательно, скорость тела 1 выше скорости тела 2

Точка пересечения прямых зависимостей координаты от времени, построенных для разных тел в одном масштабе, соответствует точке встречи этих тел.



- Равномерное прямолинейное движение
- теория по физике 🧲 кинематика
- Скорость при прямолинейном равномерном движении
- Перемещение и координаты тела при равномерном прямолинейном движении
- График проекции перемещения
- График координаты
- Конспект лекции «Равномерное прямолинейное движение»
- 1. Скорость равномерного прямолинейного движения
- 2. Уравнение прямолинейного равномерного движения
- 3. Графическое представление прямолинейного равномерного движения
- Контрольные вопросы
- Упражнения
- Литература
- Равномерное прямолинейное движение в физике — формулы и определения с примерами
- Графическое представление равномерного прямолинейного движения
- График проекции скорости
- График проекции перемещения
- График пути
- График координаты
- По графику проекции скорости можно найти проекцию перемещения и пройденный путь
- По углу наклона графика проекции перемещения можно оценить скорость движения
- Пример №1
- Пример №2
- Прямолинейное равномерное движение и скорость
- Пример №3
- Скорость при равнопеременном прямолинейном движении
- Перемещение при равнопеременном прямолинейном движении
- Равноускоренное и равнозамедленное движения
- Кинематика прямолинейного движения
- 💥 Видео
Видео:Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

Равномерное прямолинейное движение
теория по физике 🧲 кинематика
Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.
Видео:Графики зависимости пути и скорости от времениСкачать

Скорость при прямолинейном равномерном движении
Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.
Векторный способ записи скорости при равномерном прямолинейном движении: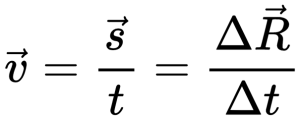
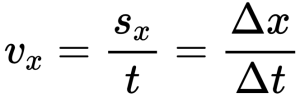
Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.
Дополнительные единицы измерения
- 1 км/ч (километр в час) = 1000 м/3600 с.
- 1 км/мин (километр в минуту) = 1000 м/60 с.
- 1 км/с (километр в секунду) = 1000 м/с.
- 1 м/мин (метр в минуту) = 1 м/60 с.
- 1 см/с (сантиметр в секунду) = 0,01 м/с.
Спидометр — прибор для измерения модули скорости тела.
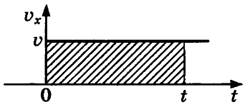
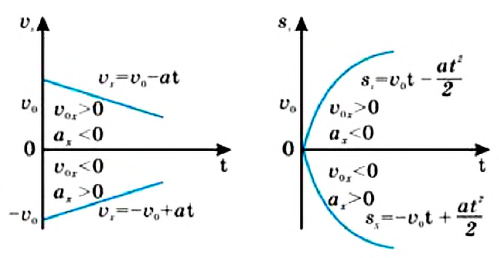
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:
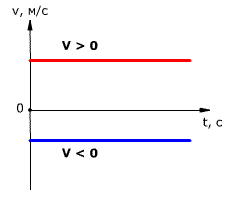
- Если график скорости лежит выше оси времени, тело движется в направлении оси ОХ.
- Если график скорости лежит ниже оси времени, тело движется против оси ОХ.
- Если график скорости совпадает с осью времени, тело покоится.
Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.
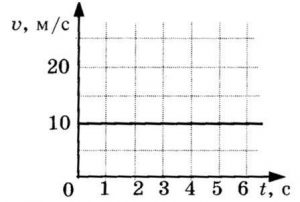
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.
График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:
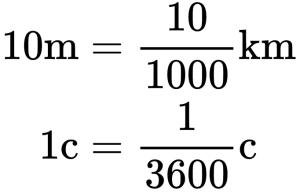
Видео:Урок 12. Равномерное прямолинейное движениеСкачать

Перемещение и координаты тела при равномерном прямолинейном движении
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.
При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:
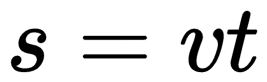
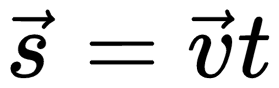
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.
Формула проекции перемещения:
График проекции перемещения
График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:
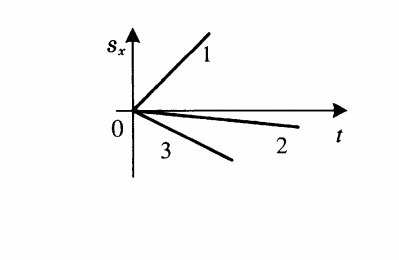
- Если луч лежит выше оси времени, тело движется в направлении оси ОХ.
- Если луч лежит ниже оси времени, тело движется против оси ОХ.
- Если луч совпадает с этой осью, тело покоится.
Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси sx.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси sx меньше.
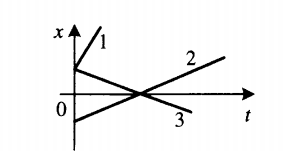
График координаты
График координаты представляет собой график зависимости координаты от времени. Выглядит он так:
Так как график координаты представляет собой график линейной функции, уравнение координаты принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Определение направления движения тела по графику координаты
- Если с течением времени координата увеличивается (график идет снизу вверх), тело движется в направлении оси ОХ. На картинке выше этому соответствуют графики тел 1 и 2.
- Если с течением времени координата уменьшается (график идет сверху вниз), тело движется противоположно направлению оси ОХ. На картинке выше этому соответствует график тела 3.
- Если координата не изменяется, тело покоится.
Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.
Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.
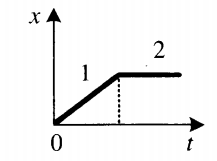
Пример №2. График зависимости координаты тела от времени имеет вид:
Изучите график и на его основании выберите два верных утверждения:
- На участке 1 скорость тела постоянна, а на участке 2 равна нулю.
- Проекция ускорения тела на участке 1 положительна, а на участке 2 — отрицательна.
- На участке 1 тело движется равномерно, а на участке 2 оно покоится.
- На участке 1 тело движется равноускорено, а на участке 2 оно движется равномерно.
- Проекция ускорения тела на участке 1 отрицательна, а на участке 2 — положительна.
На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.
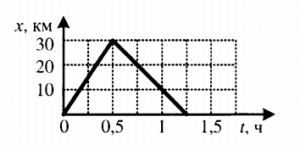
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?
Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:
Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:
Скорость во время движения от В к А равна:
Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.
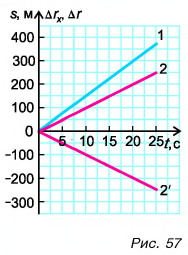
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…
Алгоритм решения
- Выбрать любой временной интервал.
- Выбрать для временного интервала начальные и конечные пути для каждого из графиков.
- Записать формулу скорости и вычислить ее для 1 и 2 тела.
- Найти n — отношение скорости второго тела к скорости первого тела
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
- Для графика 1: начальный путь s10 = 0 м. Конечный путь равен s1 = 80 м.
- Для графика 2: начальный путь s20 = 0 м. Конечный путь равен s2 = 120 м.
Скорость определяется формулой:
Так как начальный момент времени и скорость для обоих тел нулевые, формула примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Скорость первого тела:
Скорость второго тела:
Отношение скорости второго тела к скорости первого тела:
pазбирался: Алиса Никитина | обсудить разбор | оценить
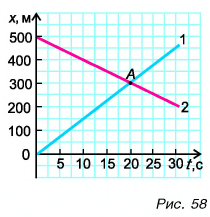
На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.
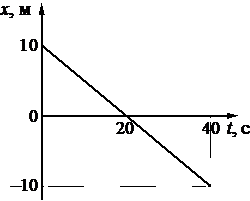
Алгоритм решения
- Записать уравнение координаты при равномерном прямолинейном движении.
- Выразить из уравнения проекцию скорости.
- Определить начальную и конечную координаты, а также время, в течение которого двигалось тело.
- Вычислить проекцию скорости.
- Выбрать соответствующий график.
Решение
Уравнение координаты при равномерном прямолинейном движении имеет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Отсюда проекция скорости равна:
Начальная координата xo = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.
Вычисляем проекцию скорости:
Этому значению соответствует график «в».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Видео:Перемещение при прямолинейном равномерном движении | Физика 9 класс #4 | ИнфоурокСкачать

Конспект лекции «Равномерное прямолинейное движение»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
Видеолекции для
профессионалов
- Свидетельства для портфолио
- Вечный доступ за 120 рублей
- 311 видеолекции для каждого
«Истинное знание — это знание причин».
РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
1. Скорость равномерного прямолинейного движения
2. Уравнение прямолинейного равномерного движения точки
3. Графическое представление равномерного прямолинейного движения
Видео:9 класс, 3 урок, Графики прямолинейного равномерного движенияСкачать

1. Скорость равномерного прямолинейного движения
Простейший вид механического движения — равномерное прямолинейное движение.
Равномерным прямолинейным движением называют движение материальной точки, при котором она за любые равные промежутки времени совершает одинаковые перемещения.
Приблизительно равномерным прямолинейным движением можно считать движение парашютиста с раскрытым парашютом вблизи поверхности Земли (в отсутствие ветра), движение эскалатора метрополитена.
Из определения равномерного прямолинейного движения следует:
– для описания данного движения достаточно воспользоваться одномерной системой координат, поскольку траектория движения — прямая;
– отношение перемещения к интервалу времени, за который это перемещение произошло, для данного движения является неизменной величиной, ведь за равные интервалы времени тело совершает одинаковые перемещения.
Движения разных тел отличаются быстротой: улитка ползёт медленно, самолёт летит быстро. Такие кинематические величины, как перемещение и путь, не содержат информацию о том, как быстро по времени изменяется положение тела в пространстве. Пространственно-временной характеристикой движения является скорость.

Дадим определение скорости равномерного прямолинейного движения. Допустим, что точка, двигаясь равномерно и прямолинейно в течение некоторого промежутка времени 



Вычислим отношение этого перемещения к промежутку времени, в течение которого это перемещение произошло. В результате будем иметь вектор, потому что при делении вектора на число, будет тоже вектор. Этот вектор получил название — скорость равномерного прямолинейного движения точки. Его обозначают буквой 
Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения точки ко времени, за которое оно совершено.
Следовательно, можно записать: 
Так как промежуток времени 

Модуль перемещения 

В Международной системе (СИ) единицей расстояния является метр, единицей времени — секунда; поэтому скорость выражается в метрах в секунду 



Скорость движения транспортных средств измеряется прибором — спидометром, где числа шкалы показывают скорость, выраженную в 
Равномерное движение — это всегда движение по прямой линии. При равномерном движении путь и перемещение одинаковы.
Например, если машина едет по прямой линии и на спидометре одно и то же значение скорости (модуль скорости), то это движение равномерное. Стоит машине изменить направление (повернуть), это будет означать, что вектор скорости изменил свое направление. Вектор скорости направлен туда же, куда едет машина. Такое движение нельзя считать равномерным, несмотря на то, что спидометр показывает одно и то же число.
Движение на карусели также нельзя считать равномерным, так как постоянно изменяется направление движения, а значит и вектор скорости.
Уравнение скорости для равномерного прямолинейного движения имеет вид 
Видео:Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

2. Уравнение прямолинейного равномерного движения
Равномерное прямолинейное движение описывается определённым уравнением. Получим это уравнение, воспользовавшись определением скорости.
Пусть радиус-вектор 




Если начальный момент времени 


Но по формулам, написанным в векторном виде, вычисления вести нельзя, ведь векторная величина имеет не только численное значение, но и направление. При вычислениях удобно пользоваться формулами, в которые входят не векторы, а их проекции на оси координат, так как над проекциями можно производить алгебраические действия.
Если тело движется равномерно вдоль положительного направления оси 







Полученное выражение является уравнением координаты тела. Его называют кинематическим уравнением равномерного движения или законом равномерного прямолинейного движения.






Перепишем кинематическое уравнение равномерного движения в виде:

Учтём также, что разность между начальной и конечной координатой точки — проекция перемещения на выбранную координатную ось:
Левые части обоих равенств равны, значит правые тоже равны. Получим уравнение для проекции перемещения:
Его называют уравнением перемещения.
При равномерном прямолинейном движении направление вектора скорости не изменяется, а значит путь и модуль проекции перемещения тела равны. На основании этого, получим уравнение пути при равномерном прямолинейном движении тела:
При равномерном прямолинейном движении зависимость пути от времени является линейной.
Если движение точки происходит по направлению оси 



Видео:Физика - уравнения равноускоренного движенияСкачать

3. Графическое представление прямолинейного равномерного движения
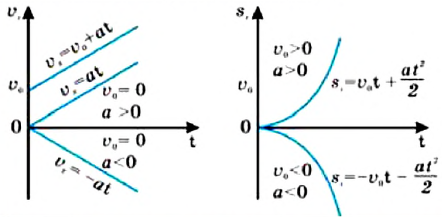
Рассмотрим графические зависимости скорости, координаты, пути и перемещения от времени при равномерном прямолинейном движении.


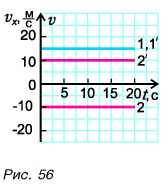
Из графика скорости видно, что проекция скорости тел для прямых 1 и 3 больше нуля, так как они располагаются выше оси времени. В случае с прямой 2 можно сказать, что тело движется в обратном направлении, поэтому проекция скорости отрицательная.
Если рассмотреть конечный промежуток времени, то получим ограниченную область, имеющую форму прямоугольника. Площадь этого прямоугольника будет являться пройденным телом путем. (Длина одной из сторон прямоугольника — это скорость, а длина другой — это промежуток времени).
2. График зависимости пройденного пути от времени.





Графики зависимости пути от времени для всех тел располагаются выше оси времени . Это объясняется тем, что пройденный путь — это длина траектории, а, следовательно, путь не может быть отрицательным.
Наклон графика пути к оси времени зависит от модуля скорости: чем больше скорость движения тела, тем больший угол наклона. Скорость движения тела равна тангенсу угла наклона прямой к оси времени:
3. Графиками движения называют графики зависимости координаты от времени .





На графике видно, что для первого и третьего тела значение координаты 

Для прямой 2 значение координаты 
Кроме того, из графиков можно судить о модуле скорости. Тело, движение которого описано прямой 1, движется быстрее остальных, так как за один и тот же промежуток времени оно проходит большее расстояние.
При этом, как и в случае с перемещением, угол наклона графика к оси времени зависит от скорости тела. Из этих наблюдений можно сделать следующий вывод: чем больше угол между прямой и осью времени, тем больше скорость движения тела.
В случае прямолинейного равномерного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти положение тела в любой момент времени.

1) координаты тела в любой момент времени;
2) путь, пройденный телом за некоторый промежуток времени;
3) время, за которое пройден какой-то путь;
4) кратчайшее расстояние между телами в любой момент времени;
5) момент и место встречи тел
Необходимо помнить , что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.
Примеры решения задач
Задача 1. На рисунке приведены графики движения двух тел. Чему равно отношение скорости первого тела к скорости второго?


Проекция скорости: 
Значит 
Искомое отношение:
Ответ: отношение скоростей равно 
Задача 2. Даны законы движения двух материальных точек: 



1 способ (аналитический)
В момент встречи:

Тогда

2 способ (графический)





Ответ: две материальные точки встретятся через 5 с в точке с координатой 15 м
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Контрольные вопросы
1. Какое движение называют равномерным прямолинейным?
2. Дайте определение скорости равномерного прямолинейного движения.
3. Как определить модуль скорости прямолинейного равномерного движения?
4. Какой вид имеет у равнение скорости для равномерного прямолинейного движения?
5. Каков физический смысл скорости?
6. Какое уравнение выражает закон равномерного прямолинейного движения?
7. Какой вид имеет уравнение перемещения при равномерном прямолинейном движении?
8. Какой вид имеет график скорости для равномерного прямолинейного движения?
9. В каких случаях график расположен выше оси времени? ниже оси времени? на оси времени?
10. Как по графику скорости определить путь, пройденный телом?
11. Как угол наклона графика зависимости пройденного пути от времени при равномерном прямолинейном движении зависит от скорости?
12. Какая зависимость отражается на графике движения?
13. Что можно определить, пользуясь графиком движения?
14. Составьте с помощью интернета таблицу примерных скоростей различных объектов. Проанализируйте её.
Видео:Скорость прямолинейного равноускоренного движения. График скорости | Физика 9 класс #6 | ИнфоурокСкачать

Упражнения
1. На рисунке изображены графики зависимости координаты от времени для пешехода и велосипедиста:

б) В каком направлении оси 
в) Чему равны модули скорости пешехода и велосипедиста?
г) Перенесите графики в тетрадь и добавьте к ним график зависимости координаты от времени для автомобиля, который едет в отрицательном направлении оси 
2. На рисунке изображены графики зависимости координаты от времени для тела, движущегося вдоль оси 
а) Какие графики описывают движение тела в направлении, противоположном направлению оси 
б) На каких графиках показано, что тело проходит через начало координат?
в) На каких графиках 


а) Каким цветом изображён график для грузовика?
б) Какому событию соответствует точка пересечения графиков?
в) Какие величины можно определить по этим графикам? Чему они равны?
г) Перенесите эти графики в тетрадь и добавьте к ним график зависимости координаты от времени для легкового автомобиля, который двигался прямолинейно и равномерно, встретился сначала с велосипедистом, а потом — с грузовиком, причём обе эти встречи произошли до того, как грузовик и велосипедист встретились друг с другом. В каком направлении относительно оси 
4. Автомобиль и мотоциклист движутся навстречу друг другу со скоростями, модули которых равны 30 м/с и 20 м/с соответственно. Расстояние между ними в начальный момент времени равно 150 м. Найдите аналитическим способом время встречи автомобиля с мотоциклистом и расстояние, которое проехал мотоциклист. Решите задачу графическим способом.
5. Муравей и черепаха движутся вдоль стены здания друг за другом. Муравей догоняет черепаху. В начальный момент времени расстояние между ними равно 75 см. Модуль скорости муравья равен 5 см/с, а модуль скорости черепахи равен 2,5 см/с. Когда муравей догонит черепаху? Решите задачу аналитическим и графическим способами.
6. Моська погналась за разозлившим её слоном. Модуль скорости слона равен 2 м/с, а модуль скорости Моськи — 12 м/с. Когда Моська догонит слона, если в начальный момент времени расстояние между ними равно 300 м?
Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Литература
1. Мякишев Г. Я., Физика 10 класс, 2016 год, стр. 20-23, 31-33
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Равномерное прямолинейное движение в физике — формулы и определения с примерами
Содержание:
Равномерное прямолинейное движение:
Вы изучали равномерное прямолинейное движение, познакомились с понятием «скорость». Скалярной или векторной величиной является скорость? Каковы закономерности равномерного прямолинейного движения?
Вы знаете, что движение, при котором за любые равные промежутки времени тело проходит одинаковые пути, называется равномерным. В каком случае одинаковыми будут не только пути, но и перемещения?
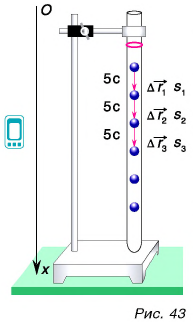
Проделаем опыт. Проследим за падением металлического шарика в вертикальной трубке, заполненной вязкой жидкостью (например, густым сахарным сиропом) (рис. 43). Будем отмечать положение шарика через равные промежутки времени. Опыт показывает, что за равные промежутки времени, например за
Сделаем вывод. При равномерном прямолинейном движении тело за любые равные промежутки времени совершает одинаковые перемещения и проходит одинаковые пути.
В 7-м классе вы находили скорость равномерного движения тела как отношение пути к промежутку времени, за который путь пройден: 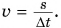
Скорость равномерного прямолинейного движения — это величина, равная отношению перемещения к промежутку времени, за который оно совершено:
Из равенства (1) следует, что скорость 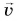
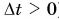
Отношение 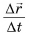
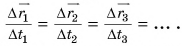
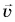
Из формулы (1) легко найти перемещение:
и путь 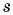
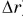
А как определить положение равномерно и прямолинейно движущегося тела в любой момент времени 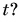
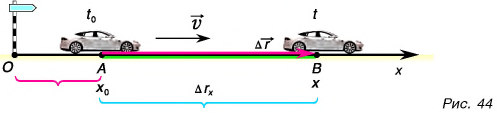
Автомобиль рассматриваем как материальную точку. Из формулы (2) находим проекцию перемещения автомобиля на ось Ох:

Согласно рисунку 44 за время 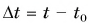
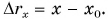
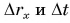
Приняв 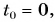
Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.
Зависимость координаты движущегося тела от времени называется кинематическим законом движения. Формула (5) выражает кинематический закон равномерного прямолинейного движения.
Для измерения скорости используются специальные приборы. В автомобилях имеется спидометр (рис. 45), на самолетах — указатель скорости. Эхолокаторы измеряют скорость тел, движущихся под водой, а радиолокаторы (радары) — в воздухе и по земле. Сотрудники службы дорожного движения с помощью портативного радара с видеокамерой (рис. 46) регистрируют скорость транспортных средств.
Для любознательных:
Скорости движения могут сильно отличаться. За одну секунду черепаха может преодолеть несколько сантиметров, человек — до 10 м, гепард — до 30 м, гоночный автомобиль — около 100 м.
Около 8 км за секунду пролетает по орбите спутник Земли (рис. 47). Но даже скорости космических кораблей «черепашьи» по сравнению со скоростью микрочастиц в ускорителях. В современном ускорителе (рис. 48) электрон за одну секунду пролетает почти 300 000 км!
Главные выводы:
- При равномерном прямолинейном движении за любые равные промежутки времени тело совершает одинаковые перемещения.
- Скорость равномерного прямолинейного движения постоянна: с течением времени не изменяется ни ее модуль, ни ее направление.
- При равномерном прямолинейном движении тела модуль перемещения равен пути, пройденному за тот же промежуток времени.
- Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.
Пример решения задачи:
Кинематический закон прямолинейного движения лодки но озеру вдоль оси Ох задан уравнением 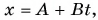
Определите: 1) проекцию скорости лодки 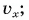
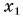
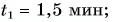
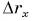
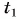
Решение
Сделаем рисунок к задаче.
По условию задачи координата лодки линейно зависит от времени. Значит, лодка движется равномерно. Сравнив 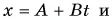
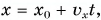
Найдем
Из рисунка 49: проекция перемещения
Ответ:
Видео:Равномерное прямолинейное движение - физика 9Скачать

Графическое представление равномерного прямолинейного движения
Зависимости между различными величинами можно наглядно изобразить с помощью графиков. Использование графиков облегчает решение научных, практических задач и даже бытовых проблем.
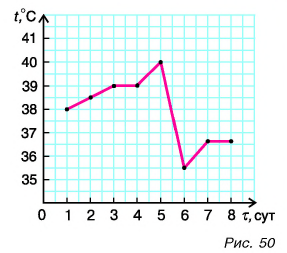
Например, по графику зависимости температуры пациента от времени (рис. 50) видно, что на 5-е сутки температура достигла своего максимума, затем резко упала, а еще через сутки стала приближаться к норме. График дал наглядное представление о течении болезни.
В физике роль графиков чрезвычайно велика. Умение строить и читать графики помогает быстрее и глубже понять физические явления.
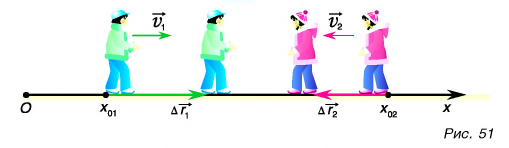
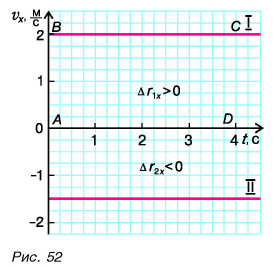
Рассмотрим простой пример из кинематики. Леша и Таня идут навстречу друг другу (рис. 51). Они движутся равномерно и прямолинейно. Модуль скорости Леши 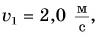
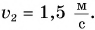
Выберем координатную ось Ох и зададим начальные положения участников движения (см. рис. 51). Пусть при 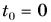
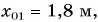
Построим графики зависимости проекции скорости 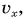
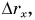
График проекции скорости
Согласно условию и рисунку 52 для проекций скорости движения Тани и Леши на ось Ох получим: 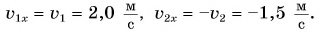
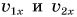
Графики показывают: проекция скорости при равномерном прямолинейном движении с течением времени не изменяется.
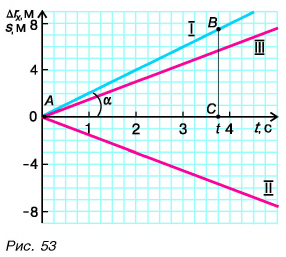
График проекции перемещения
Проекция перемещения 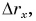
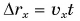
Зависимость проекции перемещения от времени для Леши 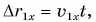
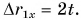
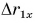
Для Тани 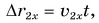
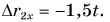
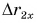
Из графиков и формул следует, что при равномерном прямолинейном движении проекция перемещения прямо пропорциональна времени.
График пути
Путь — величина положительная при любом движении тела. При равномерном прямолинейном движении путь равен модулю перемещения: 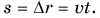
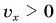
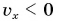
Графики пути показывают: при равномерном прямолинейном движении пройденный путь прямо пропорционален времени.
График координаты
Его называют также графиком движения.
По формуле 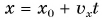
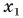
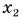
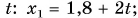
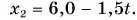
Графики движения показывают: при равномерном прямолинейном движении координата тела линейно зависит от времени.
По точке пересечения графиков I и II (точке А) (рис. 54) легко найти момент и координату места встречи Леши и Тани. Определите их самостоятельно.
Что еще можно определить по графикам?
По графику проекции скорости можно найти проекцию перемещения и пройденный путь
Рассмотрим прямоугольник ABCD на рисунке 52. Его высота численно равна 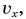
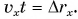
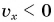
Докажите самостоятельно, что площадь между графиком проекции скорости и осью времени численно равна пройденному пути.
По углу наклона графика проекции перемещения можно оценить скорость движения
Рассмотрим треугольник АВС на рисунке 53. Чем больше угол наклона а графика проекции перемещения, тем больше скорость тела. Объясните это самостоятельно.
Главные выводы:
Для равномерного прямолинейного движения:
- График проекции скорости — прямая, параллельная оси времени.
- Графики проекции перемещения и координаты — прямые, наклон которых к оси времени определяется скоростью движения.
- Площадь фигуры между графиком проекции скорости и осью времени определяет проекцию перемещения.
Пример №1
Мотоциклист едет из города по прямолинейному участку шоссе с постоянной скоростью 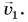
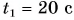
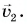
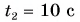
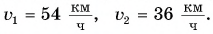
Решение
Изобразим координатную ось Ох, вдоль которой идет движение (рис. 55). Начало системы координат О свяжем с перекрестком.
В начальный момент времени мотоциклист находился на перекрестке, а велосипедист в точке В. Значит, кинематический закон движения мотоциклиста имеет вид:
Найдем координату 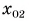
Кинематический закон движения велосипедиста имеет вид:
Расстояние между мотоциклистом и велосипедистом через время 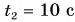
Пример №2
Построим графики проекций и модулей скорости. Для мотоциклиста графики проекции скорости 1 и модуля скорости 
Графиками пути s, проекции 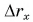
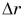
Графики пути, модуля и проекции перемещения мотоциклиста совпадают (прямая 1).
Прямая 2 является графиком пути и модуля перемещения велосипедиста. Прямая 
Графики координат представлены на рисунке 58. Они выражают зависимости 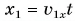
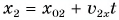
Ответ:
Прямолинейное равномерное движение и скорость
Из курса Физики VII класса вам известно, что равномерное прямолинейное движение является самым простым видом механического движения.
Прямолинейное равномерное движение — это движение по прямой линии, при котором материальная точка за равные промежутки времени совершает одинаковые перемещения.
При прямолинейном равномерном движении модуль и направление скорости с течением времени не изменяются:
Скорость при прямолинейном равномерном движении является постоянной физической величиной, равной отношению перемещения материальной точки ко времени, за которое это перемещение было совершено:
Так как отношение 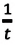
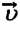
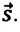
Если скорость 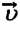
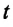
При прямолинейном равномерном движении пройденный телом путь равен модулю перемещения:
Так как уравнение в векторном виде можно заменить алгебраическими уравнениями в проекциях векторов, то для вычисления перемещения используют не формулу, выраженную через векторы, а формулу, содержащую в себе проекции векторов на координатные оси. При прямолинейном движении положение материальной точки определяется одной координатой X, определяются проекции векторов скорости и перемещения материальной точки на эту ось и уравнение решается в этих проекциях. Поэтому выражение (1.2) можно записать в проекциях перемещения и скорости на ось ОХ:
Можно получить формулу для вычисления координаты точки 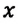
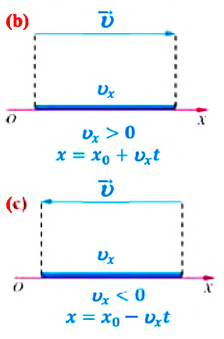
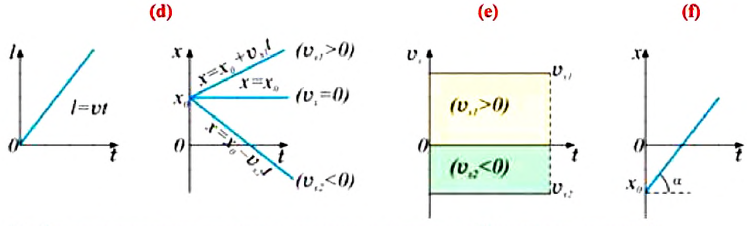
Выражение (1.5) является уравнением прямолинейного равномерного движения тела. Если материальная точка движется по направлению выбранной координатной оси ОХ, то проекция скорости считается положительной (b), если же движется против направления координатной оси, то проекция скорости считается отрицательной (с).
Из формулы (1.5) определяется выражение для проекции скорости:
Из формулы (1.6) становится ясным физический смысл скорости: проекция скорости на ось равна изменению проекции соответствующей координаты за единицу времени.
Пройденный путь и координата материальной точки при прямолинейном равномерном движении являются линейной функцией от времени (d). Скорость же является постоянной величиной, поэтому график скорость — время будет представлять собой линию, параллельную оси времени — скорость такого движения не зависит от времени (е):
График координата-время при равномерном движении образует определенный угол с осью времени. Тангенс этого угла равен проекции (модулю) скорости по оси ох (f):
Пример №3
Два велосипедиста одновременно начали движение навстречу друг другу вдоль прямой линии из пунктов А и В, расстояние между которыми 90 км. Скорость первого велосипедиста 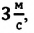
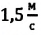
Определите: а) координату и время 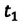
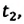
a) При решении задачи соблюдается следующая последовательность действий:
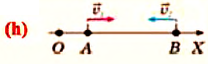
I действие. Выбирается система координат ОХ с началом координат в точке А и рисуется схема (h).
II действие. Уравнение движения записывается в общем виде:
III действие. На основании условия задачи уравнения движения велосипедистов записываются в общем виде:
IV действие. Координаты велосипедистов при встрече равны: 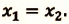
V действие. Для определения координат 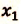
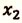
Так как 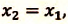
b) Так как по условию задачи велосипедисты движутся прямолинейно и без изменения направления движения, то пройденный путь равен проекции (модулю) перемещения:
c) Время 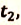
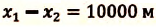
Скорость при равнопеременном прямолинейном движении
Из формулы (1.14) видно, что если известны ускорение 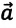
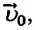
или ее проекцию на ось
Если начальная скорость равна нулю 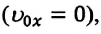
Из этих выражений видно, что скорость при равнопеременном движении является линейной функцией от времени. График зависимости скорости от времени — прямая линия, проходящая через начало координат (или через 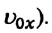
Перемещение при равнопеременном прямолинейном движении
Формулу для определения перемещения при равнопеременном движении можно вывести на основе графика скорость-время. Проекция перемещения равна площади фигуры между графиком 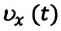
На приведенных графиках — это заштрихованная фигура трапеции (см: с):
или в векторной форме:
Если в последнюю формулу вместо 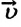
обобщенную формулу перемещения для равнопеременного движения:
Таким образом, формула проекции перемещения (например, на ось 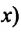
а формула координаты:
(1.23) является формулой перемещения при равнопеременном движении в векторной форме, а (1.24) и (1.25) обобщенными формулами координаты и проекции перемещения, соответственно. Если материальная точка начинает движение из состояния покоя 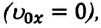
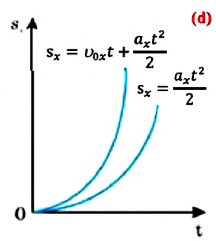
Как видно из формулы, проекция перемещения при прямолинейном равнопеременном движении пропорциональна квадрату времени 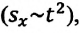
В некоторых случаях возникает необходимость определить перемещение материальной точки, не зная время 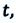
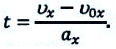
Это выражение подставляется в формулу (1.21):
После простых преобразований получаем:
Для проекции конечной скорости получаем: 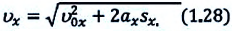
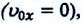
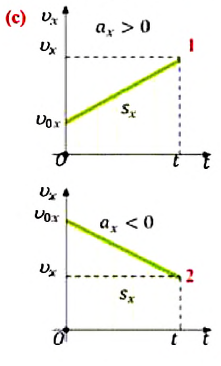
Равноускоренное и равнозамедленное движения
Равнопеременное движение по характеру может быть или равноускоренным, или же равнозамедленным.
При равноускоренном движении векторы 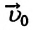
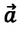
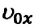
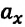
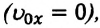
При равнозамедленном движении векторы 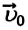
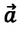
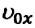
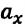
В таблице 1.3 даны формулы и соответствующие графики равноускоренного и равнозамедленного прямолинейного движения.
| Прямолинейное равноускоренное движение | |||
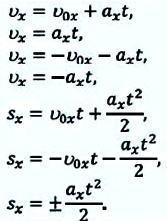 |  | ||
| Прямолинейное равнозамедленное движение | |||
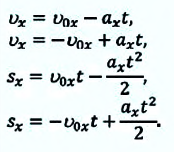 | |||
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Ускорение в физике
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
- Путь и перемещение
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💥 Видео
Урок 15. Решение задач на графики движенияСкачать

Урок 25. График скорости РУД. Перемещение при РУД.Скачать

Прямолинейное равнопеременное движение, ускорение. 9 класс.Скачать

Перемещение тела при прямолинейном равноускоренном движении | Физика 9 класс #8 | ИнфоурокСкачать

Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

7 класс, 6 урок, Графики зависимости пути и скорости от времениСкачать

Решение графических задач на равномерное движениеСкачать

Кинематика. Равномерное и равноускоренное движение. Урок 1Скачать




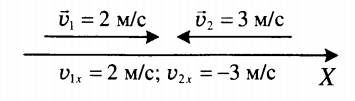
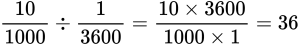
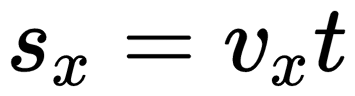
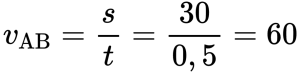
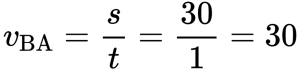






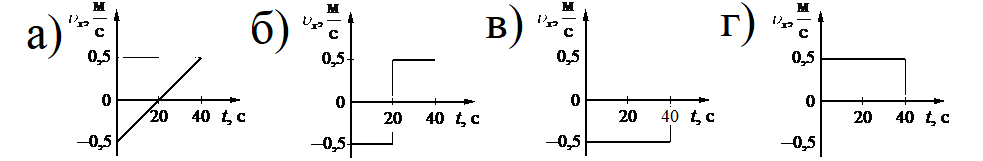
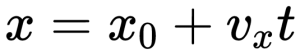
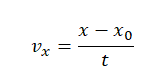
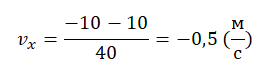




















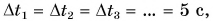



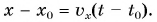






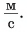
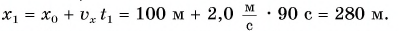
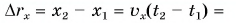
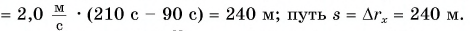
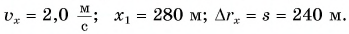
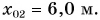

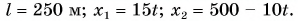
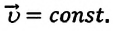
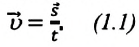
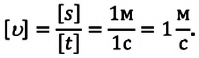

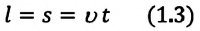
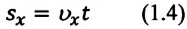
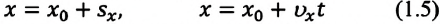
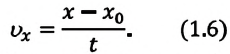
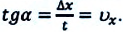
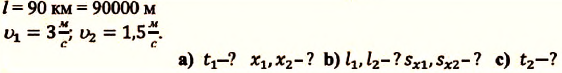
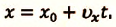
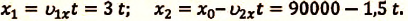
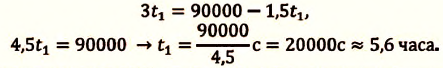
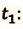
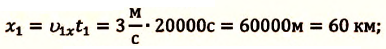
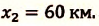
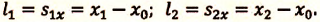
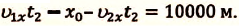
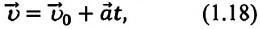
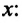
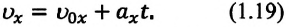

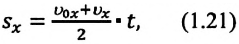
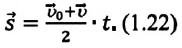
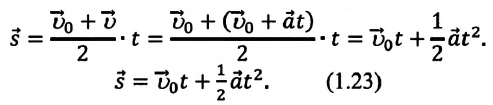
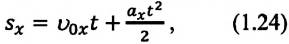
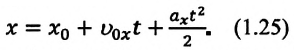
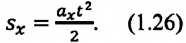
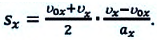

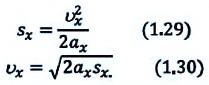
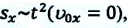 то отношение проекций перемещения равно отношению квадратов соответствующих промежутков времени:
то отношение проекций перемещения равно отношению квадратов соответствующих промежутков времени:
 — подъемная машина).
— подъемная машина).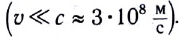
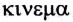 — движение) изучается механическое движение тел без учета их масс и действующих на них сил. В динамике (от греческого слова
— движение) изучается механическое движение тел без учета их масс и действующих на них сил. В динамике (от греческого слова 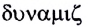 — сила) рассматривается влияние взаимодействия между телами на их движение. В статике (от греческого слова
— сила) рассматривается влияние взаимодействия между телами на их движение. В статике (от греческого слова 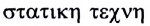 — искусство взвешивать) исследуются законы сложения сил и условия равновесия твердых, жидких и газообразных тел.
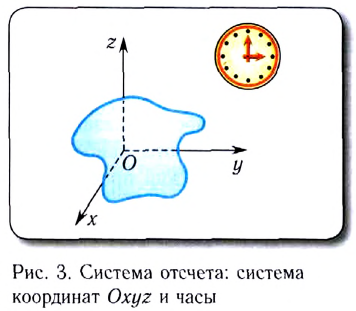
— искусство взвешивать) исследуются законы сложения сил и условия равновесия твердых, жидких и газообразных тел.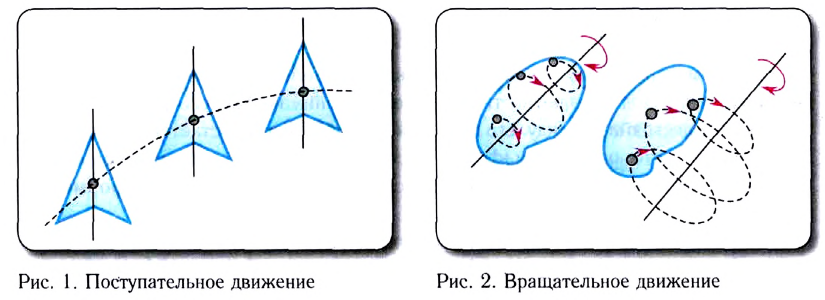
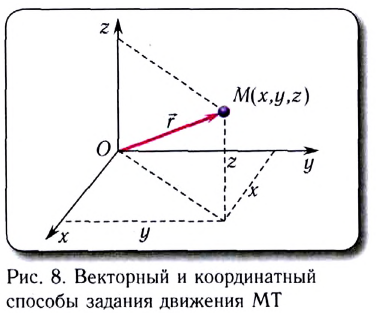
 направленный из точки, заданной радиус-вектором
направленный из точки, заданной радиус-вектором 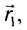 где МТ находилась в начальный момент времени, в точку, заданную радиус-вектором
где МТ находилась в начальный момент времени, в точку, заданную радиус-вектором 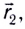 где МТ находится в рассматриваемый момент времени (рис. 4):
где МТ находится в рассматриваемый момент времени (рис. 4):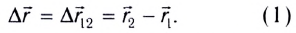
 всегда проводится из начала координат О в текущее положение материальной точки (рис. 8). При движении положение МТ изменяется. Закон движения в этом случае задается векторным уравнением
всегда проводится из начала координат О в текущее положение материальной точки (рис. 8). При движении положение МТ изменяется. Закон движения в этом случае задается векторным уравнением 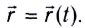
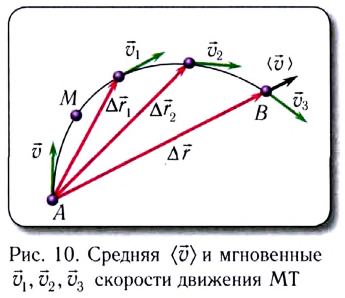
 движения как отношение перемещения
движения как отношение перемещения 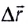 тела к промежутку времени
тела к промежутку времени 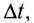 за который это перемещение произошло (рис. 10):
за который это перемещение произошло (рис. 10):
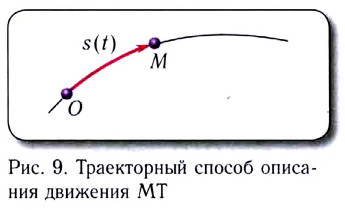
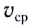 называется отношение длины отрезка пути As (см. рис. 9) к промежутку времени
называется отношение длины отрезка пути As (см. рис. 9) к промежутку времени 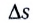 его прохождения:
его прохождения:
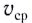 в отличие от средней скорости
в отличие от средней скорости 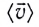 является скалярной величиной.
является скалярной величиной.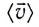 характеризует движение тела (МТ) на определенном участке траектории, но не дает информации о его движении в определенной точке траектории или в определенный момент времени. Кроме того, средняя скорость дает лишь приближенное понятие о характере движения, так как движение в течение каждого малого промежутка времени заменяется равномерным движением. В рамках этой модели скорость тела (МТ) меняется скачком при переходе от одного промежутка времени к другому.
характеризует движение тела (МТ) на определенном участке траектории, но не дает информации о его движении в определенной точке траектории или в определенный момент времени. Кроме того, средняя скорость дает лишь приближенное понятие о характере движения, так как движение в течение каждого малого промежутка времени заменяется равномерным движением. В рамках этой модели скорость тела (МТ) меняется скачком при переходе от одного промежутка времени к другому.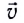 — это скорость тела (МТ), равная производной перемещения по времени:
— это скорость тела (МТ), равная производной перемещения по времени:
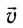 в любой точке траектории направлен по касательной к ней (см. рис. 10).
в любой точке траектории направлен по касательной к ней (см. рис. 10).
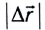 равен пройденному пути s. Скорость
равен пройденному пути s. Скорость 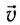 равномерного движения равна отношению перемещения тела
равномерного движения равна отношению перемещения тела 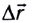 ко времени
ко времени 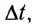 за которое это перемещение произошло:
за которое это перемещение произошло:
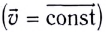 и равна средней скорости
и равна средней скорости 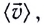 определяемой выражением (2).
определяемой выражением (2).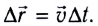 Вследствие того, что
Вследствие того, что 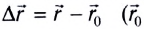 — радиус-вектор, задающий положение МТ в начальный
— радиус-вектор, задающий положение МТ в начальный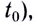 получаем кинематическое уравнение движения в векторном виде
получаем кинематическое уравнение движения в векторном виде
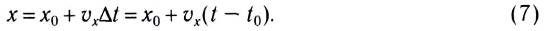
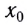 — координата тела (МТ) в начальный момент времени
— координата тела (МТ) в начальный момент времени 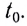 Если начальный момент времени
Если начальный момент времени 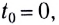 уравнение принимает вид
уравнение принимает вид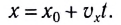
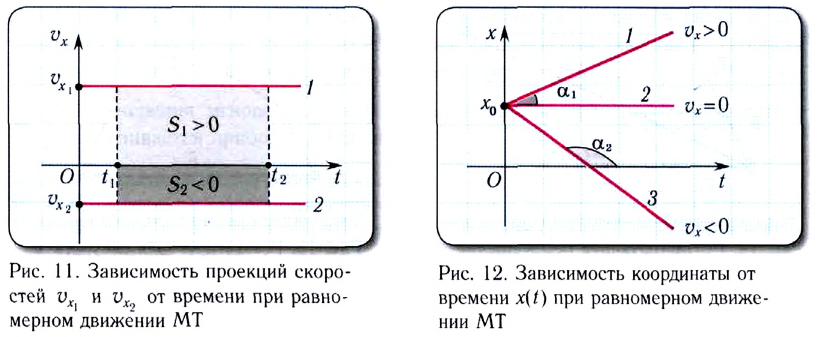
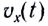 от времени представляет собой отрезок прямой линии, параллельной оси времени Ot (рис. 11). Отрезок прямой l на рисунке 11 соответствует движению материальной точки в положительном направлении оси
от времени представляет собой отрезок прямой линии, параллельной оси времени Ot (рис. 11). Отрезок прямой l на рисунке 11 соответствует движению материальной точки в положительном направлении оси 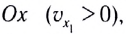 а 2 — в отрицательном
а 2 — в отрицательном 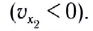 Площади
Площади 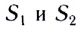 закрашенных прямоугольников численно равны модулям перемещений МТ с проекциями скоростей
закрашенных прямоугольников численно равны модулям перемещений МТ с проекциями скоростей 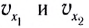 за промежуток времени
за промежуток времени 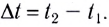
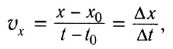
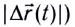 от времени s(t) при равномерном движении представляет собой прямую линию, проходящую через начало координат (рис. 13).
от времени s(t) при равномерном движении представляет собой прямую линию, проходящую через начало координат (рис. 13).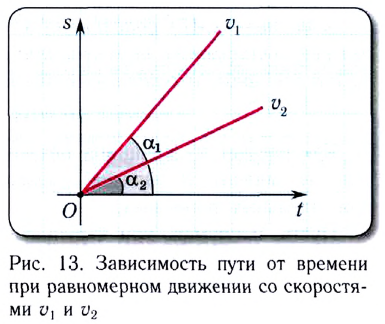
 ).
).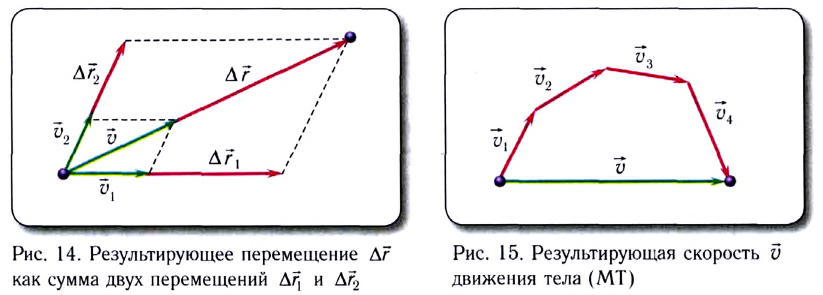

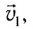 мы движемся на лодке со скоростью
мы движемся на лодке со скоростью 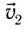 относительно воды. В этом случае результирующее перемещение
относительно воды. В этом случае результирующее перемещение 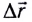 (рис. 14) лодки относительно берега будет складываться из собственного перемещения
(рис. 14) лодки относительно берега будет складываться из собственного перемещения 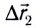 относительно воды и перемещения
относительно воды и перемещения 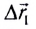 вместе с водой вследствие течения реки:
вместе с водой вследствие течения реки: 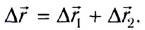
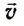 тела (МТ), участвующего в нескольких движениях одновременно, равна векторной сумме скоростей
тела (МТ), участвующего в нескольких движениях одновременно, равна векторной сумме скоростей  отдельных движений (рис. 15):
отдельных движений (рис. 15):