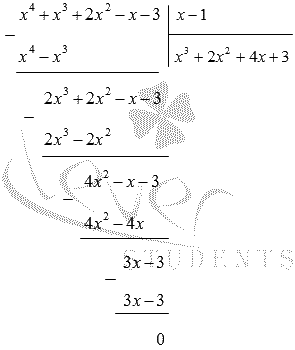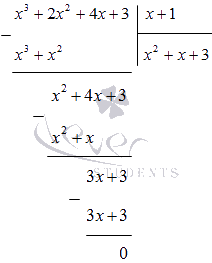Разделы: Математика
В классах с углубленным изучением математики уравнения степени выше второй начинают изучать сразу же после прохождения темы «Квадратные уравнения». В курсе алгебры 8-9 классов – это уравнения, которые путем тех или иных преобразований сводятся к квадратным. Чтобы помочь учащимся разобраться в многообразии этих уравнений, я разбиваю их на типы в соответствии с методом их решения. Это облегчает их усвоение, а так же подготавливает учащихся к усвоению темы «Уравнения высших степеней» в 10-11 классах. Все рассмотренные уравнения можно предложить и учащимся общеобразовательных классов, которые интересуются математикой. Уравнения, аналогичные разобранным, можно найти в сборниках и учебной литературе, список которой приведен в конце работы.
а) биквадратные уравнения
б) с модулем
в) введение новой переменной
д) уравнения, в которых во всех квадратных трехчленах равны соответственно старший коэффициент и свободный член
е) сводящееся с помощью введения новой переменной к дробно-линейному
Литература
- Ю.Н.Макарычев, Н.Г. Миндюк. Алгебра. Дополнительные главы к школьному учебнику 8 класса. Учебное пособие для учащихся школ и классов с углубленным изучением математики. Под ред. Г.В.Дорофеева. Москва «Просвещение» 1997 и последующие издания.
- Ю.Н.Макарычев, Н.Г. Миндюк. Алгебра. Дополнительные главы к школьному учебнику 9 класса. Учебное пособие для учащихся школ и классов с углубленным изучением математики. Под ред. Г.В.Дорофеева. Москва «Просвещение» 1997 и последующие издания.
- Ю.Н.Макарычев, Н.Г. Миндюк. Дидактические материалы по алгебре для 8 класса с углубленным изучением математики. Москва «Просвещение» 2001 и последующие издания.
- Ю.Н.Макарычев, Н.Г. Миндюк. Дидактические материалы по алгебре для 9 класса с углубленным изучением математики. Москва «Просвещение» 2001 и последующие издания.
- М.Л. Галицкий, А.М.Гольдман, Л.И.Звавич. Сборник задач пол алгебре для 8-9 классов. Учебное пособие для учащихся школ и классов с углубленным изучением математики. Москва 1996 и последующие издания.
- Л.И.Звавич, Д.И.Аверьянов, Б.П. Пигарев, Т.Н.Трушанина. Задания для проведения письменного экзамена по математики в 9 классе. Москва «Просвещение» 1994 и последующие издания.
Видео:Теорема БезуСкачать

Решение уравнений высших степеней
В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Видео:Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать

Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :
a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .
Видео:8 класс, 35 урок, Уравнения высших степенейСкачать

Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .
Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:
Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:
x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )
Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :
— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3 .
D = 1 2 — 4 · 1 · 3 = — 11 0
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| x i | коэффициенты многочлена | ||||
| 1 | 1 | 2 | — 1 | — 3 | |
| 1 | 1 | 1 + 1 · 1 = 2 | 2 + 2 · 1 = 4 | — 1 + 4 · 1 = 3 | — 3 + 3 · 1 = 0 |
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
После нахождения следующего корня, равного — 1 , мы получаем следующее:
| x i | коэффициенты многочлена | |||
| 1 | 2 | 4 | 3 | |
| 1 | 1 | 2 + 1 · ( — 1 ) = 1 | 4 + 1 · ( — 1 ) = 3 | 3 + 3 · ( — 1 ) = 0 |
Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.
Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .
Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .
Решение
У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .
Проверяем их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
| x i | коэффициенты многочлена | ||||
| 1 | — 1 | — 5 | 0 | 12 | |
| 2 | 1 | — 1 + 1 · 2 = 1 | — 5 + 1 · 2 = — 3 | 0 — 3 · 2 = 3 | 12 — 6 · 2 = 0 |
В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .
Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.
2 3 + 2 2 — 3 · 2 — 6 = 0
Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :
| x i | коэффициенты многочлена | |||
| 1 | 1 | — 3 | — 6 | |
| 2 | 1 | 1 + 1 · 2 = 3 | — 3 + 3 · 2 = 3 | — 6 + 3 · 2 = 0 |
В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .
Ответ: x = — 3 2 ± i 3 2 .
Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.
Решение
x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0
Выполняем домножение 2 3 обеих частей уравнения:
2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0
Заменяем переменные y = 2 x :
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Ответ: x 1 = — 1 , x 2 = 3 2
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Методическая разработка по алгебре на тему «Решение уравнений высших степеней» (8 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Министерство образования Республики Марий Эл
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 3 г. Козьмодемьянска»
элективного курса по математике
«Решение алгебраических уравнений
Разработала: учитель математики
высшей квалификационной категории
МОУ «СОШ № 3 г Козьмодемьянска»
Республики Марий Эл
Авдеева Галина Николаевна
Элективный курс «Решение уравнений высших степеней» предназначен для предпрофильной подготовки в 9 классе, а так же может быть использован для изучения в профильных 10 – 11 классах. Актуальность этого курса состоит в том, что в последние годы в материалах выпускных экзаменов в форме ОГЭ и ЕГЭ предлагаются задания по этой теме. Курс предназначен для углубления знаний учащихся по теме «Уравнения» и рассчитан на 10 часов. Содержание курса согласовано с государственными стандартами общего среднего образования и примерными программами по математике.
Предлагаемый элективный курс соответствует возрастным особенностям учащихся, не создает у них перегрузок при изучении математики.
Курс ориентирован на развитие у школьника умений решать уравнения более сложные, чем предлагаются в учебнике, выбирать оптимальный метод решения для данного конкретного уравнения.
Данный элективный курс может быть использован учителями общеобразова- тельных классов для индивидуальных и дифференцированных занятий.
• развитие математической культуры учащихся;
• развитие познавательной деятельности учащихся;
• развитие интереса школьников к предмету.
• расширить представления учащихся по важнейшей теме в курсе алгебры;
• познакомить учащихся с различными методами решения уравнений;
• развивать логическое мышление, умение аргументировать ответы.
• умение учащихся решать уравнения различными методами;
• применение полученных знаний для успешной сдачи ОГЭ и ЕГЭ;
• определение склонностей ученика при выборе профильного обучения.
Виды деятельности на занятиях:
• лекция, практикум, беседа.
По окончании курса учащиеся должны выполнить практическую работу: подготовить подборку уравнений рассмотренных видов из дополнительной литературы (с решениями).
Методы решения уравнений высших степеней.
1. Метод разложения на множители.
1)

х = − 3. Пусть 

Ответ: −3; 
2)


Ответ: 1; 
2. Метод введения новой переменной.
Это самый распространенный метод.
а) Простейшие случаи. Очевидная замена.
1)
Пусть 
Получаем: 
х = 1 
Ответ: 
2)
Пусть 





D = 9 – 28 = − 19 D = 9 + 16 = 25
корней нет 

3)
Пусть 

Имеем два уравнения:




D = 1 – 24 = − 23 

4)
Пусть 



х − 1 = − 1 или х − 1 = 1 х − 1 = − 2 или х − 1 = 2
5)
Пусть 

Имеем два уравнения:




х = 0; х = − 1
Ответ: − 1; 0; 
б) Использование основного свойства дроби
1)
Т. к. х = 0 не является корнем уравнения, то разделим и числитель, и знаменатель каждой дроби на х ≠ 0.
Пусть 

Возвращаемся к переменной х.

D = 49 – 60 = − 11 D = 49 – 15 = 34
корней нет
Ответ: 
2)
Т. к. х = 0 не является корнем уравнения, то разделим и числитель, и знаменатель каждой дроби на х ≠ 0.
Пусть 


t = 1;
Возвращаемся к переменной х.

D = 1 – 24 = − 23 D = 121 – 96 = 25
в) Раскрытие скобок парами
1)
Пусть 

Получаем два квадратных уравнения:

х = 2; х = 3; D = 25 + 64 = 89
Ответ: 2; 3; 
2)
Пусть 






D = 9 + 24 = 33 х = − 5; х = 2
Ответ: − 5; 2; 
г) Раскрытие скобок парами и деление обеих частей уравнения
Т. к. х = 0 не является корнем уравнения, то обе части уравнения разделим
на 
Пусть 


Получаем два уравнения с переменной х:

Ответ: −4; 5; 
д) Выделение квадрата двучлена.
Пусть 
Имеем два уравнения:


х = − 1; х = 2; D = 25 – 40 = − 15
е) Возвратные уравнения
Определение. Возвратным уравнением называют уравнение, в котором
равноудаленные от концов уравнения коэффициенты равны.
1)
Т. к. х = 0 не является корнем уравнения, то обе части уравнения разделим
на 
Пусть 

D = 25 + 1200 = 1225
Имеем два уравнения с переменной х:



х = − 3; 

Ответ: − 3; 

2)
Т. к. х = 0 не является корнем уравнения, то обе части уравнения разделим
на 
Пусть 

Имеем два уравнения с переменной х:


х = 
Ответ: 

ж) Уравнения, сводящиеся к однородному уравнению
1)
Разделим обе части уравнения на 
Пусть 


Возвращаемся к переменной х:



х = 1; 

Ответ: 0; 1; 

Пусть 

с двумя переменными:
Подставим в эти равенства выражения с переменной х:

х = 1; 

Ответ: 0; 1; 

2)
Пусть 

с двумя переменными:
Ответ: − 1; − 0,5; 2; 4.
з) Уравнения, содержащие взаимно обратные выражения.
1)
Пусть 

Получаем уравнение: 



(х + 1) 2 = 0 D = 1 – 16 = − 15
х = − 1 корней нет
2)
Пусть 

Получаем уравнение: 





3х – 1 = 8х + 20; 3х – 1 = − 8х − 20; 12х – 4 = 2х + 5; 12х – 4 = − 2х − 5;
5х = − 21 11х = − 19 10х = 9 14х = − 1
х = − 4,2 х = 

Ответ: − 4,2; 

3. Применение следствия из теоремы Безу.
Если число α является корнем многочлена Р(х), то этот многочлен делится на
1)
Подбором находим, что число 2 является корнем уравнения. Значит, левая
часть уравнения делится на х – 2. Получаем:
х + 5 = 0 или х 2 – 3 = 0
Ответ: −5; 2; 
2)
Подбором находим, что число 1 является корнем уравнения. Значит, левая
часть уравнения делится на х – 1. Получаем:
Подбором находим, что число −1 является корнем уравнения. Значит, левая
часть уравнения делится на х + 1. Получаем:
Подбором находим, что число −2 является корнем уравнения. Значит, левая
часть уравнения делится на х + 2. Получаем:
Ответ: −2; −1; 1; 
Для самостоятельного решения:
1.
Ответ: 1; 

2.
Ответ: 
3.
Ответ: − 4; 
4.
5.
Ответ: 

6.
Ответ: −3; 2; 3; 4; 5.
7.
Ответ: −1; 23; 

8.
Ответ: − 

9.
Ответ: −2; 3;
10.
1. А.Г. Мордкович. Алгебра – 8 . Часть 1. Учебник. Мнемозина, 2013 год.
2. А.Г. Мордкович и др. Алгебра – 8. Часть 2. Задачник. Мнемозина, 2013 год
3. А.Г. Мордкович, Н.П. Николаев. Алгебра – 8. Учебник для классов с
углублённым изучением математики. Мнемозина, 2010 год.
4. Л.И. Звавич, А.Р. Рязановский. Алгебра – 8. Задачник для классов с
углублённым изучением математики. Мнемозина, 2010 год.
5. А.Г. Мордкович. Алгебра – 9 . Часть 1. Учебник. Мнемозина, 2013 год.
6. А.Г. Мордкович и др. Алгебра – 9. Часть 2. Задачник. Мнемозина, 2013 год
7. А.Г. Мордкович, Н.П. Николаев. Алгебра – 9. Учебник для классов с
углублённым изучением математики. Мнемозина, 2009 год.
8. Л.И. Звавич, А.Р. Рязановский, П.В. Семёнов. Алгебра – 9. Задачник для
классов с углублённым изучением математики. Мнемозина, 2009 год.
9. М.Л.Галицкий, А.М.Гольдман, Л.И.Звавич. Сборник задач по алгебре. 8 – 9
🎦 Видео
Вспоминаем схему Горнера и уравнения высших степенейСкачать

✓ Теорема Безу. Рациональные нули многочленов | Ботай со мной #119 | Борис ТрушинСкачать

11 класс, 3 урок, Уравнения высших степенейСкачать

Уравнения высших степеней 1 часть (старший коэффициент равен 1)Скачать

Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Уравнение четвертой степениСкачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Решение уравнения методом замены переменнойСкачать

Решение систем уравнений второго порядка. 8 класс.Скачать

Метод неопределенных коэффициентовСкачать

(Урок 8 класс 18/05)Уравнения высших степенейСкачать

Теорема Виета для уравнений высших степеней. Рациональные уравнения Часть 4 из 4Скачать

Уравнения высших степеней. Решение уравнений с помощью деления в столбикСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать