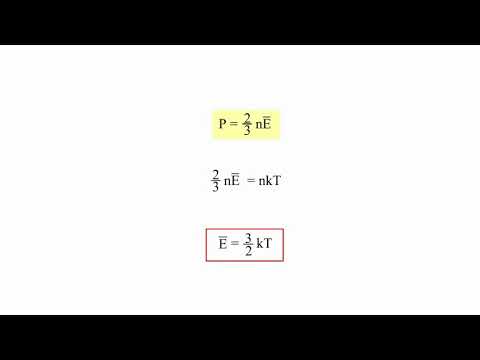МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ – раздел молекулярной физики, изучающий свойства вещества на основе представлений об их молекулярном строении и определенных законах взаимодействия между атомами (молекулами), из которых состоит вещество. Считается, что частицы вещества находятся в непрерывном, беспорядочном движении и это их движение воспринимается как тепло.
До 19 в. весьма популярной основой учения о тепле была теория теплорода или некоторой жидкой субстанции, перетекающей от одного тела к другому. Нагревание тел объяснялось увеличением, а охлаждение – уменьшением содержащегося внутри них теплорода. Понятие об атомах долго казалось ненужным для теории тепла, однако многие ученые уже тогда интуитивно связывали тепло с движением молекул. Так, в частности, думал русский ученый М.В.Ломоносов. Прошло немало времени, прежде чем молекулярно-кинетическая теория окончательно победила в сознании ученых и стала неотъемлемым достоянием физики.
Многие явления в газах, жидкостях и твердых телах находят в рамках молекулярно-кинетической теории простое и убедительное объяснение. Так давление, оказываемое газом на стенки сосуда, в котором он заключен, рассматривается как суммарный результат многочисленных соударений быстро движущихся молекул со стенкой, в результате которых они передают стенке свой импульс. (Напомним, что именно изменение импульса в единицу времени приводит по законам механики к появлению силы, а сила, отнесенная к единице поверхности стенки, и есть давление). Кинетическая энергия движения частиц, усредненная по их огромному числу, определяет то, что принято называть температурой вещества.
Истоки атомистической идеи, т.е. представления о том, что все тела в природе состоят из мельчайших неделимых частиц-атомов, восходят еще к древнегреческим философам – Левкиппу и Демокриту. Более двух тысяч лет назад Демокрит писал: «…атомы бесчисленны по величине и по множеству, носятся же они во вселенной, кружась в вихре, и таким образом рождается все сложное: огонь, вода, воздух, земля». Решающий вклад в развитие молекулярно-кинетической теории был внесен во второй половине 19 в. трудами замечательных ученых Дж.К.Максвелла и Л.Больцмана, которые заложили основы статистического (вероятностного) описания свойств веществ (главным образом, газов), состоящих из огромного числа хаотически движущихся молекул. Статистический подход был обобщен (по отношению к любым состояниям вещества) в начале 20 в. в трудах американского ученого Дж.Гиббса, который считается одним из основоположников статистической механики или статистической физики. Наконец, в первые десятилетия 20 в. физики поняли, что поведение атомов и молекул подчиняется законам не классической, а квантовой механики. Это дало мощный импульс развитию статистической физики и позволило описать целый ряд физических явлений, которые ранее не поддавались объяснению в рамках обычных представлений классической механики.
- Молекулярно-кинетическая теория газов.
- Давление газа.
- Уравнение состояния. Газовые законы.
- МУ 4866: Изучение сил вязкого трения
- Элементы теории и метод эксперимента
- Метод Стокса
- Вязкости некоторых веществ (в мкПа·с)
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Вязкость газов по молекулярно-кинетической теории (мкт)
- 🌟 Видео
Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Молекулярно-кинетическая теория газов.
Газовое состояние (см. ГАЗ) – одно из тех состояний вещества, описание которого на основе методов молекулярно-кинетической теории уже с самого начала ее развития дало наиболее полные и ощутимые результаты. В первую очередь это относится к так называемому идеальному газу, молекулы которого большую часть времени проводят в состоянии свободного хаотического движения, резко меняя свою скорость лишь в моменты кратковременных столкновений. Молекулярно-кинетическая теория успешно объясняет все известные экспериментальные законы идеального газа (закон Бойля – Мариотта, закон Гей-Люссака, закон Авогадро и формулируемое на их основе уравнение состояния Менделеева – Клапейрона). На базе этой теории получили свое полное объяснение процессы переноса в газах: диффузия, вязкость и теплопроводность.
Видео:Идеальный газ в молекулярно-кинетической теории | Физика 10 класс #28 | ИнфоурокСкачать

Давление газа.
В качестве одного из примеров применения молекулярно-кинетической теории можно рассмотреть вывод выражения для давления газа. Сначала определяется среднее число столкновений молекул, происходящих за единицу времени с поверхностью стенки сосуда. В газе выделяются три взаимно перпендикулярных оси, соответствующие декартовой системе координат. Если в сосуде содержится N молекул, то из-за огромного их числа логично предположить, что в любой момент времени вдоль каждого из направлений будут двигаться примерно N/3 молекул. Очевидно, что в направлении самой стенки сосуда перпендикулярно к ней будет в среднем двигаться 1/6 часть всех молекул.
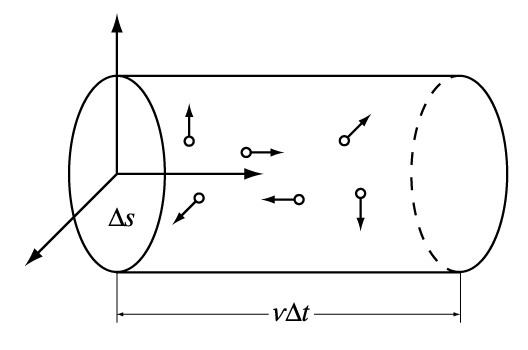
Пусть есть плоский элемент поверхности на стенке сосуда D S. Предполагается, для простоты, что все молекулы движутся с одинаковой скоростью v. Тогда за время D t до элемента стенки D S долетят все движущиеся по направлению к нему молекулы, которые заключены в объеме цилиндра с основанием D S и высотой v D t (рис. 1).
Если n = N/V – число молекул в единице объема, то число молекул, долетевших до стенки и ударившихся об нее, равно D v = (n/6)v D S D t. Соответственно, число ударов молекул об единичную площадку в единицу времени оказывается равным
Каждая молекула, летящая к стенке, при столкновении с ней передает стенке свой импульс. Поскольку скорость молекулы при упругом столкновении со стенкой меняется от величины v до –v, величина передаваемого импульса равна 2mv. Сила, действующая на поверхность стенки D S за время D t, определяется величиной полного импульса, передаваемого всеми молекулами достигнувшим стенки за этот промежуток времени, т.е. F = 2mv n c D S/ D t, где n c определено выражением (1). Для величины давления p = F/ D S в этом случае находим: p = (1/3)nmv2.
Для получения окончательного результата можно отказаться от предположения об одинаковой скорости молекул, выделив независимые группы молекул, каждая из которых имеет свою приблизительно одинаковую скорость. Тогда средняя величина давления находится усреднением квадрата скорости по всем группам молекул или
Это выражение можно представить также в виде
где 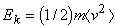
Тепловое равновесие, понятие температуры. Известно, что тепло всегда перетекает от горячего тела к холодному, т.е. температура соприкасающихся тел стремится выравняться. Это явление характеризуют как переход системы в состояние теплового равновесия. Понятие температуры является не столь очевидным, как многие привычные понятия механики: масса, сила, энергия и т.д. Температура связана с весьма неопределенным понятием теплоты и холода, которые располагаются в сознании человека где-то рядом с запахом и вкусом. Одно из главных достижений молекулярно-кинетической теории состоит в том, что теплота рассматривается просто как одна из форм энергии, а именно – кинетическая энергия атомов и молекул. Эта величина, усредненная по огромному числу беспорядочно движущихся частиц, и оказывается мерилом того, что называется температурой тела. Такое представление распространяется на все вещества – твердые, жидкие и газообразные. Частицы нагретого тела движутся быстрее, чем холодного. Если два тела, имеющие первоначально разные температуры, входят в соприкосновение друг с другом, движение частиц в одном из них замедляется, в другом наоборот ускоряется: средняя кинетическая энергия частиц становится везде одинаковой. Это и означает, что система в целом приходит в состояние полного теплового равновесия.
Поскольку понятие температуры тесно связано с усредненной кинетической энергией молекул, было бы естественным и в качестве единиц ее измерения использовать энергетические единицы (например, эрг или джоуль). Однако, энергия теплового движения частиц фактически очень мала по сравнению с эргом (не говоря уже о джоуле), поэтому использование этой величины оказывается неудобным. В молекулярной физике пользуются практически удобной условной единицей измерения температуры – градусом, который определяется таким образом, что интервал температур между точками кипения и замерзания воды при атмосферном давлении полагается равным 100 градусам.
Если температура T измеряется в градусах Кельвина (К), то связь ее со средней кинетической энергией молекул имеет вид
где k = 1,38·10 –16 эрг/K – переводный коэффициент, определяющий, какая часть эрга содержится в градусе. Величина k называется постоянной Больцмана (она была введена Планком в 1899).
Видео:Основные положения молекулярно-кинетической теории газов и ее опытное обоснование. 10 класс.Скачать

Уравнение состояния. Газовые законы.
Подстановка соотношений (4) в (3), приводит к известному уравнению состояния идеального газа
Из соотношений (2) и (5) следует также выражение для средне-квадратичной скорости молекул
Этой формуле удобно придать другой вид, умножив числитель и знаменатель под знаком квадратного корня на число Авогадро
Здесь M = mNA – атомная или молекулярная масса, величина R = kNA = 8,318·10 7 эрг называется газовой постоянной.
Средняя скорость молекул в газе даже при умеренных температурах оказывается очень большой. Так, для молекул водорода (H2) при комнатной температуре (T = 293K) эта скорость равна около 1900 м/c , для молекул азота в воздухе – порядка 500 м/с. Скорость звука в воздухе при тех же условиях равна 340 м/с.
Учитывая, что n = N/V, где V – объем, занимаемый газом, N – полное число молекул в этом объеме, легко получить следствия из (5) в виде известных газовых законов. Для этого полное число молекул представляется в виде N = vNA, где v – число молей газа, и уравнение (5) принимает вид
которое носит название уравнения Клапейрона – Менделеева.
При условии T = const давление газа меняется обратно пропорционально занимаемому им объему (закон Бойля – Мариотта).
В замкнутом сосуде фиксированного объема V = const давление меняется прямо пропорционально изменению абсолютной температуры газа Т. Если газ находится в условиях, когда постоянным сохраняется его давление p = const, но изменяется температура (такие условия можно осуществить, например, если поместить газ в цилиндр, закрытый подвижным поршнем), то объем, занимаемый газом, будет меняться пропорционально изменению его температуры (закон Гей-Люссака).
Пусть в сосуде есть смесь газов, т.е. имеются несколько разных сортов молекул. В этом случае величина импульса, передаваемого стенке молекулами каждого сорта, не зависит от наличия молекул других сортов. Отсюда следует, что давление смеси идеальных газов равно сумме парциальных давлений, которые создавал бы каждый газ в отдельности, если бы занимал весь объем. В этом состоит еще один из газовых законов – известный закон Дальтона.
Длина свободного пробега молекул. Одним из первых, кто еще в 1850-х дал разумные оценки величины средней тепловой скорости молекул различных газов, был австрийский физик Клаузиус. Полученные им непривычно большие значения этих скоростей сразу же вызвали возражения. Если скорости молекул действительно так велики, то запах любого пахучего вещества должен был бы практически мгновенно распространяться из одного конца замкнутого помещения в другой. На самом деле распространение запаха происходит очень медленно и осуществляется, как теперь известно, посредством процесса так называемой диффузии в газе. Клаузиус, а затем и другие исследователи, сумели дать убедительное объяснение этому и другим процессам переноса в газе (таким как теплопроводность и вязкость) с помощью понятия средней длины свободного пробега молекул, т.е. среднего расстояния, которое пролетает молекула от одного столкновения до другого.
Каждая молекула в газе испытывает очень большое число столкновений с другими молекулами. В промежутке между столкновениями молекулы движутся практически прямолинейно, испытывая резкие изменения скорости лишь в момент самого столкновения. Естественно, что длины прямолинейных участков на пути молекулы могут быть различными, поэтому имеет смысл говорить лишь о некоторой средней длине свободного пробега молекул.
За время D t молекула проходит сложный зигзагообразный путь, равный v D t. Изломов траектории на этом пути столько, сколько произошло столкновений. Пусть Z означает число столкновений, которое испытывает молекула в единицу времени Средняя длина свободного пробега равна тогда отношению длины пути 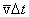
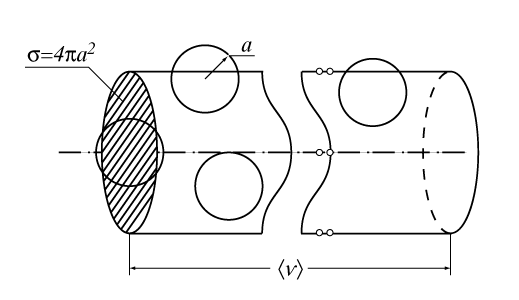
Для оценки величины Z принимается, что молекулы представляют собой твердые упругие шарики радиуса a, которые равномерно распределены в объеме газа с плотностью n. Сначала предполагается, что молекула движется в среде, где все остальные молекулы неподвижны. Можно видеть, что молекула пролетает мимо другой молекулы, не испытав столкновения с ней, если расстояние между центрами молекул превышает 2a. Следовательно, за время t, равное 1c, молекула взаимодействует только с теми партнерами по столкновению, центры которых расположены в объеме цилиндра длиной 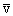
Величину s называют эффективным поперечным сечением столкновений молекул. Число молекул в объеме цилиндра равно n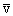
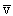
На самом деле, конечно, в газе одновременно находятся в движении все молекулы, поэтому в выражение для Z должна входить средняя скорость относительного движения молекул, так что Z = n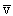
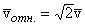
Характерный радиус молекул для различных газов можно оценить из экспериментальных данных по вязкости (внутреннему трению) в газе. Для молекул N2, например, a » 2,0·10 –10 м. В таблице 1 приведены рассчитанные по формуле (10) значения l 0 в мкм (1мкм = 10 –6 м) для некоторых газов при нормальных условиях (p = 1атм, T=273K). Эти значения оказываются примерно в 100–300 раз больше собственного диаметра молекул.
Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. Практическая часть.10 классСкачать

МУ 4866: Изучение сил вязкого трения
Лабораторная работа 1-8: Изучение сил вязкого трения
Цель работы: изучение явления вязкого трения и одного из методов определения вязкости жидкостей.
Видео:Молекулярно-кинетическая теория | ЕГЭ по физике 2023 | Снежа Планк из ВебиумСкачать

Элементы теории и метод эксперимента
При движении тел в жидкостях и газах на тела действуют силы внутреннего трения. Эти силы присущи всем реальным жидкостям и газам и составляют основу понятия вязкости. Вязкость − важная физическая характеристика веществ. Значение вязкости приходится учитывать при перекачивании жидкостей и газов по трубам (нефтепроводы, газопроводы), вязкость расплавленного стекла определяет процесс его выработки, большую роль играет вязкость в процессах выплавки металлов и т.д.
В физике явление вязкости относится к так называемым явлениям переноса. К ним также относятся явления диффузии (на молекулярно-кинетическом уровне объяснение явления связано с переносом вещества – атомов или молекул) и теплопроводности (перенос энергии при столкновениях молекул). С точки зрения молекулярно-кинетической теории вязкость объясняется переносом импульса при взаимодействии молекул.
При ламинарном течении жидкости или газа между слоями, движущимися с различной скоростью, действуют силы, обусловленные вязкостью. Если два слоя
площадью S (рис. 1) находятся на расстоянии ∆z и движутся с различными скоростями, так что ∆v = v2 – v1, между ними возникает сила вязкого трения, пропорциональная градиенту скорости ∆v/∆z в направлении, перпендикулярном к направлению течения, и площади слоев S. Этот эмпирический закон открыл Ньютон (Newton, 1687 г.):
где коэффициент η по определению называется вязкостью или коэффициентом внутреннего трения.
Из формулы (1) видно, что вязкость измеряется в паскаль-секундах (Па·с). Используют и более мелкую единицу вязкости − пуаз (П), названную так в честь французского физика Пуазейля: 1 Па·с = 10 П.
Движение жидкости (газа) в круглой трубе. Рассмотрим ламинарное течение жидкости (газа) в трубе радиусом R (рис. 2).
Выделим в этой трубе трубку длиной L меньшего радиуса r. На внешнюю поверхность этой трубки будет действовать сила, обусловленная вязкостью:
При равномерном движении эта сила должна быть равна равнодействующей сил давления, влияющих на торцы этого малого цилиндрика, ограничивающего поверхность трубки:
Из условий F+Fтр=0 получаем дифференциальное уравнение для v(r):
Решением этого уравнения с учетом того, что вблизи стенок трубы скорость течения равна нулю, будет:
Из условий F+Fтр=0 получаем дифференциальное уравнение для v(r):
Из условий F+Fтр=0 получаем дифференциальное уравнение для v(r):
Отсюда скорость течения на оси трубы:
С учетом этого можно записать:
Таким образом, изменение скорости по сечению трубы получается параболическим.
Найдем расход (поток) жидкости Q = ΔV/Δt , т.е. объем жидкости, протекающей через поперечное сечение трубы за единицу времени. Разобьем поперечное сечение трубы на кольца шириной dr (рис.3).
Через кольцо радиусом r за секунду пройдет объем жидкости, равный произведению площади кольца 2πrdr на скорость течения в точках, находящихся на расстоянии r от оси трубы:
Полный поток получается интегрированием:
Из (9) и (6) получим формулу для потока:
Формула (10) называется формулой Пуазейля (Poiseuille, 1840). Согласно этой формуле поток жидкости пропорционален перепаду давления на единице длины трубы, пропорционален четвертой степени радиуса трубы и обратно пропорционален коэффициенту вязкости.
Вязкость газов по молекулярно-кинетической теории (MKT). В газах вязкость обусловлена столкновением молекул, в жидкостях − межмолекулярным взаимодействием, ограничивающим подвижность молекул.
Рассмотрим два слоя газа, движущихся с разными скоростями (рис. 1). Если температура газа всюду одинакова, то средняя скорость движения молекул равна:
где т − масса молекулы.
Так как молекула может двигаться по шести независимым направлениям в пространстве, то площадку S за единицу времени пересечет N = unS/6 молекул, где п − концентрация молекул. Так как молекулы сталкиваются, проходя в среднем определенное расстояние, приблизительно равное средней длине свободного пробега λ, то импульс, связанный с направленным движением слоев со скоростями v1 и v2, будет передаваться слою, находящемуся между ними, если расстояние до него равно длине свободного пробега молекул, при этом изменение импульса молекул среднего слоя за время ∆t будет
Так как v(z) есть непрерывная функция координаты z, можно считать, что v2=v(z+λ), а v1=v(z-λ). Если размеры сосуда, в котором находится газ, много больше длины свободного пробега, то, полагая что λ можно считать очень малым изменением аргумента функции v(z), из определения производной следуют приближенные равенства:
Если подставить эти выражения в формулу для изменения импульса и учесть, что по второму закону Ньютона изменение импульса равно импульсу силы (∆p = F∆t), то из определения понятия коэффициента внутреннего трения с учетом того, что произведение массы молекулы на их концентрацию есть плотность газа (ρ = nm), для вязкости получается выражение:
Это выражение можно преобразовать. По молекулярно-кинетической теории длина свободного пробега молекул
где d − эффективный диаметр молекулы.
Подставив u и λ в выражение для вязкости, получим
Видим, что вязкость зависит от параметров молекулы (т и d) и от температуры газа, а от давления и плотности не зависит.
Значения вязкости некоторых жидких и газообразных веществ даны в приложении. Расплавленные металлы имеют вязкость того же порядка, что и обычные жидкости.
Так как при повышении температуры подвижность молекул увеличивается, вязкость при этом уменьшается (на примере воды это показано в приложении).
Особыми вязкостными свойствами обладает жидкий гелий. При температуре ниже 2,172 К (а температура перехода его в жидкое состояние при нормальном атмосферном давлении, т.е. температура кипения, равна 4,4 К, и при дальнейшем понижении температуры он остается жидкостью, не переходя в твердое состояние) он переходит в сверхтекучее состояние, в котором вязкость равна нулю. Это явление открыл в 1938 г. П.Л.Капица (Нобелевская премия, 1978).
Метод Стокса
Одним из методов измерения вязкости веществ (вискозиметрии) является метод падающего
шарика, или метод Стокса (Stokes, 1851 г.). Английский физик Стокс показал, что на шарик, движущийся со скоростью v в вязкой среде, действует сила вязкого трения, равная F=3πηvd , где d − диаметр шарика.
Рассмотрим движение шарика при его падении. По второму закону Ньютона (рис. 4)
где А — сила вязкого трения, FA =1/6*(ρжπd 3 g) — сила Архимеда, mg= 1/6*(ρπd 3 g) — сила тяжести, ρж и ρ — плотности жидкости и материала шариков соответственно. Решением этого дифференциального уравнения будет следующая зависимость скорости от времени:
где v0 — начальная скорость шарика, а
— скорость установившегося движения (при t>>τ). Величина τ= ρd 2 /η есть время релаксации.
Эта величина показывает, насколько быстро устанавливается стационарный режим движения. Обычно считают, что при t ≈ 3τ движение практически не отличается от стационарного. Следовательно, измерив скорость vy, можно рассчитать вязкость жидкости.
Условие ламинарности движения жидкости определяется значением безразмерного параметра − числом Рейнольдса:
где d − характерный размер движущегося тела (в данном случае диаметр шарика). Формула Стокса применима для значений R Порядок выполнения работы
- Измерить с помощью штангенциркуля внутренний диаметр сосуда, с помощью линейки − расстояние между горизонтальными метками на сосуде и с помощью микрометра − диаметры всех шариков, используемых в эксперименте. Ускорение силы тяжести считать равным 9,8 м/с 2 . Плотность жидкости и плотность вещества шариков указаны на лабораторной установке. Результаты занести в таблицу.
- Опуская поочередно шарики в жидкость, измерить время прохождения каждого из них на отрезке пути между метками. По формуле (20) вычислить вязкость жидкости η. Результаты занести в таблицу.
- Оценить погрешность результатов измерений и получить окончательный результат для значения η.
4. По формуле (19) определить значение числа Рейнольдса для одного из опытов и сделать вывод о применимости формулы Стокса.
5. Оценить путь, пройденный шариком до установления стационарного режима. Очевидно, что за время t пройденный путь определяется интегралом:
Показать, что при t = 3τ путь s = 2vyτ, и оценить эту величину.
Сравнить полученное значение с расстоянием, проходимым шариком от поверхности жидкости до верхней метки, и сделать вывод, можно ли к моменту прохождения шариком верхней метки считать его движение установившимся.
Приложение
Вязкости некоторых веществ (в мкПа·с)
Вязкость воды при разных температурах
| Температура, °С | 0 | 20 | 40 | 60 | 80 | 100 |
| η | 1790 | 1010 | 660 | 470 | 360 | 280 |
Вязкость некоторых жидкостей (при 20 о С)
| Ацетон | Бензин | Глицерин | Кастор. масло | Скипидар | Спирт |
| 330 | 650 | 1,5·10 6 | 0,99·10 6 | 1500 | 1200 |
Вязкость некоторых газов (при 20 о С)
| Азот | Водород | Воздух | Кислород | Окись углерода | Углекислый газ |
| 17,5 | 8,8 | 18,1 | 20,2 | 18,4 | 16,0 |
Видео:10 класс, 2 урок, Основное уравнение молекулярно кинетической теорииСкачать

КОНТРОЛЬНЫЕ ВОПРОСЫ
- Объяснить молекулярно-кинетический механизм явления внутреннего трения.
- Дать определение понятия вязкости и единиц ее измерения.
- Какие измерения вносят наибольшую погрешность в результат косвенного измерения вязкости жидкости в ваших опытах?
- Что такое ламинарное и турбулентное течения?
- Имеется 2 шарика из одинакового материала, но различного размера. Какой шарик будет быстрее падать в вязкой жидкости? Когда шарик быстрее падает в вязкой жидкости: в узком сосуде или в широком?
Видео:Основные положения молекулярно-кинетической теории | Физика 10 класс #24 | ИнфоурокСкачать

БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Савельев И.В. Курс общей физики. Т. 1. – М.: Наука, 1979 (и по- следующие издания). – С. 252-256, 258-261, 400-404.
- Трофимова Т.И. Курс физики: учеб. пособие для вузов. − М.: Высш.шк., 2001. – С. 62-66.
Изучение сил вязкого трения: методические указания к лабораторной работе / Рязан. гос. радиотехн. ун-т; сост.: Ю.В. Черкасова, А.С. Иваников. – Рязань, 2015. – 8 с.
Содержат элементы теории и метод определения вязкости жидкостей. Предназначены для студентов всех специальностей, изучающих дисциплину «Физика».
Табл. 1. Ил. 4. Библиогр.: 2 назв.
Вязкое трение, ламинарное течение, метод Стокса, число Рейнольдса
Печатается по решению редакционно-издательского совета Рязанского государственного радиотехнического университета.
Рецензент: кафедра общей и экспериментальной физики РГРТУ (зав. кафедрой доц. М.В. Дубков)
Изучение сил вязкого трения
Составители: Черкасова Юлия Вадимовна
Иваников Александр Сергеевич
Редактор Р.К. Мангутова Корректор С.В. Макушина
Подписано в печать 02.02.15. Формат бумаги 60 x 84 1/16.
Бумага писчая. Печать трафаретная. Усл. печ. л. 0,5.
Тираж 200 экз. Заказ
Рязанский государственный радиотехнический университет.
Видео:Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать

Вязкость газов по молекулярно-кинетической теории (мкт)
Рассмотрим два слоя газа, движущиеся с разными скоростями (рис. 1). Если температура газа всюду одинакова, то средняя скорость движения молекул также одинакова, обозначим ее И. По МКТ она зависит от массы молекул и температуры газа:

Где Т — Масса молекулы, Т — температура газа, K – постоянная Больцмана.
Так как молекула может двигаться по шести независимым направлениям в пространстве, то площадку S За единицу времени пересечет 

Так как V(Z) есть непрерывная функция координаты Z, можно считать, что V2=V(Z+λ,), а V1=V(Z-λ). Если размеры сосуда, в котором находится газ, много больше средней длины свободного пробега, то, полагая λ малым изменением аргумента функции V(Z), можно записать следующие приближенные равенства:

Если подставить эти выражения в формулу (7) и учесть, что по второму закону Ньютона изменение импульса равно импульсу силы (DР=FDT), то из определения понятия коэффициента внутреннего трения с учетом того, что произведение массы молекулы на их концентрацию есть плотность газа (ρ=Пт), для вязкости получается выражение:

Это выражение можно преобразовать. По молекулярно-кинетической теории средняя длина свободного пробега молекул

Где D — эффективный диаметр молекулы.
Подставив (8) и (9) в выражение для вязкости, получим

Видим, что вязкость зависит от массы молекулы Т, ее диаметра D И от температуры T, а от давления и плотности газа не зависит.
Вязкости некоторых веществ (в МкПа·с)
🌟 Видео
Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Идеальный и реальный газ | Газы.Молекулярно-кинетическая теория | Химия (видео 7)Скачать

Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

Физика 10 класс : Основное уравнение молекулярно-кинетической теории идеального газаСкачать

Урок 139. Основные положения МКТ.Скачать

Уравнение идеального газа. Пример 1 | Газы.Молекулярно-кинетическая теория | Химия ( видео 2)Скачать

Физика. МКТ: Основное уравнение МКТ. Центр онлайн-обучения «Фоксфорд»Скачать

Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Физика. 10 класс. Основные положения молекулярно-кинетической теории газов /16.11.2020/Скачать

МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ (МКТ)Скачать