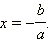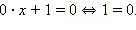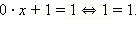Уравнения видов ax b и ax b 0 называются линейными уравнениями (7 видео)

Линейные уравнения. Виды линейных уравнений.

Линейное уравнение — это алгебраическое уравнение. В этом уравнении полная степень составляющих его многочленов равна единице.

Линейные уравнения представляют в таком виде:

Содержание

Линейное уравнение с одной переменной.
Линейное уравнение с двумя переменными.
Уравнения видов ax b и ax b 0 называются линейными уравнениями
Линейное уравнение
теория по математике 📈 уравнения
🌟 Видео

Видео:Решение линейного уравнения ax=b. Сколько корней может быть у линейного уравнения. Алгебра 7 класс.Скачать

Линейное уравнение с одной переменной.

Линейное уравнение с 1-ой переменной приводится к виду:

Число корней зависимо от a и b:

— Когда a=b=0, значит, у уравнения есть неограниченное число решений, так как .

— Когда a=0, b≠ 0, значит, у уравнения нет корней, так как .

— Когда a ≠ 0, значит, у уравнения есть только один корень .

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Линейное уравнение с двумя переменными.

Уравнением с переменной x является равенство типа A(x)=B(x), где A(x) и B(x) — выражения от x. При подстановке множества T значений x в уравнение получаем истинное числовое равенство, которое называется множеством истинности этого уравнения либо решение заданного уравнения, а все такие значения переменной — корни уравнения.

Линейные уравнения 2-х переменных представляют в таком виде:

— в общей форме: ax + by + c = 0,

— в канонической форме: ax + by = -c,

— в форме линейной функции: y = kx + m, где .

Решением либо корнями этого уравнения является такая пара значений переменных (x;y), которая превращает его в тождество. Этих решений (корней) у линейного уравнения с 2-мя переменными неограниченное количество. Геометрической моделью (графиком) данного уравнения есть прямая y=kx+m.

Если в уравнении есть икс в квадрате, то такое уравнение называется квадратным уравнением.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Уравнения видов ax b и ax b 0 называются линейными уравнениями

Уравнение вида , где − переменная, − некоторые действительные числа, называется уравнением степени не выше первой .

Если , то решением уравнения является любое число.

Если и , то уравнение корней не имеет.

Если , то уравнение называется линейным и имеет ровно одно решение

Корнем этого уравнения является число 1, поскольку при подстановке вместо этого числа получается верное числовое равенство.

Решите уравнение 0 ∙ + 1 = 0.

Имеем:

Это уравнение не имеет решений, поскольку ни при каких значениях переменной (которая, очевидно, явно не входит в уравнение) равенство не имеет место.

Ответ. Нет решений.

Решите уравнение 0 ∙ + 1 = 1.

Имеем

Решением этого уравнения является любое действительное число. В самом деле, при любом значении переменной равенство является верным.

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Линейное уравнение

теория по математике 📈 уравнения

Уравнение – это равенство, содержащее переменную, значение которой надо найти.

Уравнение с одним неизвестным, содержащим первую степень, называется линейным уравнением с одной переменной. Стандартный

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Так, например, к линейным относятся уравнения:

6х+21=0; 34–2х=0; 34х=17; 89х=0

Уравнения, содержащие несколько слагаемых с переменной или без нее, а также скобки, называются уравнениями, сводящимися к линейным. То есть при его упрощении должно получиться линейное уравнение стандартного вида. К таким уравнениям могут относиться уравнения вида:

х+12=4х–45; 19х–67=98; х=–32+17х; 7(х+13)=89–14х

Решить уравнение – это значит найти все его корни или доказать, что корней нет.

Что такое корень уравнения?

Вспомним, что корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.

Корни линейного уравнения

Наличие корней зависит от коэффициентов а и b.

Если а=0, то уравнение не имеет корней;
Если а=0 и b=0, то корней бесконечное множество (корнем является любое число);
Если а≠0 – уравнение имеет единственный корень b:а.

Рассмотрим нахождение количества корней на примерах.

Здесь коэффициент а отличен от нуля. Значит, уравнение имеет один корень.

Здесь коэффициент а равен нулю, поэтому корней нет.

Здесь оба коэффициента равны нулю, поэтому уравнение имеет множество корней, или, еще можно сказать, что корнем уравнения является любое число.

Чтобы найти корни уравнения, надо его решить, используя алгоритм, по которому из одного уравнения мы сможем получить уравнение, равносильное данному. Сначала вспомним, что при переносе слагаемых из одной части в другую, мы получаем уравнение, равносильное данному. Также можно делить или умножать обе части уравнения на одно и то же число.

Алгоритм решения линейного уравнения

Раскрыть скобки (при их наличии), используя правило раскрытия скобок;
Выполнить перенос слагаемых их одной части в другую (слагаемые с переменной собираем в одной части, слагаемые без переменной – в другой);
Привести подобные слагаемые;
Найти корень уравнения.

Пример №2. Решить уравнение:

В данном уравнении нет скобок, поэтому выполняем перенос слагаемых, изменяя соответственно знаки у тех слагаемых, которые переносим (обычно слагаемые с переменной собираем слева, а без переменной – справа): 2х–9х=10+11. Теперь приводим подобные слагаемые и получаем: –7х=21. Видим, что корень находится действием деления (неизвестный множитель): х=21:(–7). Ответ х=–3.

При оформлении решения запись оформляем следующим образом:

Пример №3. Решить уравнение:

Здесь мы видим скобки, поэтому сначала раскроем их, помня о том, то число 2 в левой части уравнения надо умножить на каждое слагаемое в скобках, а в правой части уравнения перед скобкой стоит «минус», поэтому изменяем знаки у слагаемых при раскрытии скобок: 5х–2х+16=9х–3х–11. Выполняем перенос слагаемых: 5х–2х–9х+3х=–11–16. Приводим подобные: –3х=–27. Находим корень уравнения: х=–27:(–3). Получаем ответ: х=9

Пример №4. Решить уравнение:

Выполним всё по алгоритму: перенос слагаемых и приведение подобных слагаемых. 2х–2х=3+12; 0х=15. Видим, что коэффициент а=0, поэтому запишем ответ – нет корней, так как надо 15:0, а мы знаем правило, что на нуль делить нельзя.

Имеем линейное уравнение:

Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.

Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.

Запись решения выглядит так:

pазбирался: Даниил Романович | обсудить разбор | оценить