Разделы: Математика
Тема тригонометрических уравнений начинается со школьной лекции, которая строится в виде эвристической беседы. На лекции рассматривается теоретический материал и образцы решения всех типовых задач по плану:
- Простейшие тригонометрические уравнения.
- Основные методы решения тригонометрических уравнений.
- Однородные уравнения.
На следующих уроках начинается самостоятельная отработка навыков, основанная на применении принципа совместной деятельности учителя и ученика. Сначала устанавливаются цели для учащихся, т.е. определяется, кто хочет знать не более того, что требуется государственным стандартом, а кто готов заниматься больше.
Итоговая диагностика создается с учетом уровневой дифференциации, что позволяет учащимся осознанно определять тот минимум знаний, который необходим для получения оценки “3”. Исходя из этого, отбираются разноуровневые материалы для диагностики знаний учащихся. Такая работа позволяет осуществить индивидуальный подход к учащимся, включить каждого в осознанную учебную деятельность, формировать навыки самоорганизованности и самообучения, обеспечивать переход к активному, самостоятельному мышлению.
Семинар проводится после отработки основных навыков решения тригонометрических уравнений. За несколько уроков до семинара ученикам даются вопросы, которые будут рассматриваться на нем.
Семинар состоит из трех частей.
1. Во вводной части рассматривается весь теоретический материал, включая знакомство с проблемами, которые возникнут при решении сложных уравнений.
2. Во второй части рассматриваются решение уравнений вида:
- а cosx + bsinx = c.
- a (sinx + cosx) + bsin2x + c = 0.
- уравнения, решаемые через понижение степени.
В этих уравнениях применяются универсальная подстановка, формулы понижения степени, метод вспомогательного аргумента.
3. В третьей части рассматриваются проблемы потери корней и приобретение посторонних корней. Показывается, как надо отбирать корни.
Ученики работают в группах. Для решения примеров вызываются хорошо подготовленные ребята, которые могут показать и объяснить материал.
Семинар рассчитан на хорошо подготовленного ученика, т.к. на нем рассматриваются вопросы несколько выходящие за рамки программного материала. В него включены уравнения более сложного вида, и особо рассматриваются проблемы, возникающие при решении сложных тригонометрических уравнений.
Семинар проводился для учеников 10 – 11 классов. Каждый ученик получил возможность расширить и углубить свои знания по этой теме, сравнить уровень своих знаний не только с требованиями, предъявляемыми к выпускнику школы, но и с требованиями предъявляемыми поступающим в В.У.З.
СЕМИНАР
Тема: «Решение тригонометрических уравнений»
Цели:
- Обобщить знания по решению тригонометрических уравнений всех типов.
- Заострить внимание на проблемах: потеря корней; посторонние корни; отбор корней.
I. Вводная часть
1. Основные методы решения тригонометрических уравнений
- Разложение на множители.
- Введение новой переменной.
- Функционально-графический метод.
2. Некоторые типы тригонометрических уравнений.
- Уравнения, сводящиеся к квадратным уравнениям, относительно cos х = t, sin х = t.
Asin 2 x + Bcosx + C = 0; Acos 2 x + Вsinx + C = 0.
Решаются методом введения новой переменной.
- Однородные уравнения первой и второй степени
Уравнение первой степени: Asinx + Bcosx = 0 разделим на cos x, получим Atg x + B = 0
Уравнение второй степени: Asin 2 x + Bsinx cosx + Сcos 2 x = 0 разделим на cos 2 x, получим Atg 2 x + Btgx + C = 0
Решаются методом разложения на множители и методом введения новой переменной.
- Уравнение вида: Аsinx + Bcosx = C. А, В, С
0
- Понижение степени:
1). Аcos2x + Вcos 2 x = C; Acos2x + Bsin 2 x = C.
Решаются методом разложения на множители.
2). Asin2x + Bsin 2 x = C; Asin2x + Bcos 2 x = C.
- Сводятся к однородным: С = С(sin 2 х + cos 2 х).
- Сводятся к уравнению: Аsin2x + Bcos2x = C.
- Уравнение вида: A(sinx + cosx) + Bsin2x + C = 0.
Сводятся к квадратным относительно t = sinx + cosx; sin2x = t 2 – 1.
3. Формулы.
- Универсальная подстановка:
х

+ 2
n; Проверка обязательна!
- Понижение степени: cos 2 x = (1 + cos2x): 2; sin 2 x = (1 – cos 2x): 2
- Метод вспомогательного аргумента.
Acosx + Bsinx заменим на Csin (x +
), где
sin
= а/С; cos
= в/С;

4. Правила.
- Увидел квадрат – понижай степень.
- Увидел произведение – делай сумму.
- Увидел сумму – делай произведение.
5. Потеря корней, лишние корни.
- Потеря корней: делим на g(х); опасные формулы (универсальная подстановка). Этими операциями сужаем область определения.
- Лишние корни: возводим в четную степень; умножаем на g(х) (избавляемся от знаменателя). Этими операциями расширяем область определения.
II. Примеры тригонометрических уравнений
1. Уравнения вида Asinx + Bcosx = C
1)Универсальная подстановка.О.Д.З. х – любое.
3 sin 2x + cos 2x + 1= 0.
tgx = u. х 


tg x = –1/3, x = arctg (–1/3) + 

Проверка: 3sin( 





х = 

Ответ: х = arctg(–1/3) + 




2)Функционально-графический метод. О.Д.З. х – любое.
Sinx – cosx = 1
Sinx = cosx + 1.
Построим графики функций: y = sinx, y = cosx + 1.
Ответ: х = 






3) Введение вспомогательного аргумента. О.Д.З.: х – любое.
8cosx + 15 sinx = 17.
8/17 cosx + 15/17 sinx = 1, т.к. (8/17) 2 + (15/17) 2 = 1, то существует такое 

cos 



sin (x + 
Ответ: x = 





2. Понижение порядка: Acos2x + Bsin2x = C. Acos2x + Bcos2x = C.
1). sin 2 3x + sin 2 4x + sin 2 6x + sin 2 7x = 2. О.Д.З.: х – любое.
1 – cos 6x + 1 – cos 8x + 1 – cos 12x + 1 – cos 14x = 4
cos 6x + cos 8x + cos 12x + cos 14x = 0
2cos10x cos 4x + 2cos 10x cos 2x = 0
2cos 10x(cos 4x + cos 2x) = 0
2cos10x 2cos3x cosx = 0
cos10x = 0, cos3x = 0, cosx = 0.
Ответ: х = 








| При | k = 1 и m = 0 k = 4 и m = 1. | серии совпадают. |
3. Сведение к однородному. Asin2x + Bsin 2 x = C, Asin2x + Bcos 2 x = C.
1) 5 sin 2 x + 
5 sin 2 х + 

cos 2 х = 0 удовлетворяет уравнению.
cosx ( 
cosx = 0, 
х = 






Ответ: х = 





4. Уравнение вида: А(sinx + cosx) + В sin2x + С = 0.
1). 4 + 2sin2x – 5(sinx + cosx) = 0. О.Д.З.: х – любое.
sinx + cosx = t, sin2x = t 2 – 1.
4 + 2t 2 – 2 – 5t = 0, | t | 2 – 5t + 2 = 0. t1 = 2, t2 = Ѕ.
sinx + cosx = Ѕ. cosx = sin(x + 
sinx +sin(x + 
2sin(x + 

sin(x + 

x +


Ответ: х = (–1) k arcsin(1/2



5. Разложение на множители.
1) cos 2 х – 2 cosx = 4 sinx – sin2x
cosx(cosx – 2) = 2 sinx (2 – cosx),
(cosx – 2)(cosx + 2 sinx) = 0.
1) сosx = 2, корней нет.
2) сosx + 2 sinx = 0
2tgx + 1 = 0
Ответ: x = arctg(1/2) + 

III. Проблемы возникающие при решении тригонометрических уравнений
1. Потеря корней: делим на g(х); применяем опасные формулы.
1) Найдите ошибку.
1 – сosx = sinx *sinx/2,
1 – сosx = 2sin 2 х/2 формула.
2 sin 2 х/2 = 2 sinx/2* сosx/2* sinx /2 разделим на 2 sin 2 х/2,
1 = сosx/2
х/2 = 2 


Потеряли корни sinx/2 = 0, х = 2

Правильное решение: 2sin 2 х/2(1 – сosx /2) = 0.
| sin 2 х/2 = 0 x = 2  k, k k, k  Z. Z. | 1 – сosx /2 = 0 x = 4p n, n  Z. Z. |
2. Посторонние корни: освобождаемся от знаменателя; возводим в четную степень.
1). (sin4x – sin2x – сos3x + 2sinx – 1) : (2sin2x – 

2сos3х sinx – сos3x + 2sinx – 1 = 0
(сos3x + 1)(2sinx – 1) = 0
| 1). сos3x + 1 = 0 х =  /3 + 2 /3 + 2 n/3, n n/3, n  Z. Z. | 2). 2sinx – 1 = 0 x = (–1) k  /6 + /6 +  k, k k, k  Z. Z. |
I. х =  /3 + 2 /3 + 2 n/3 n/3 1. n = 0 sin 2  /3 = /3 =  3 / 2 3 / 2 не удовлетворяют. О.Д.З. 2. n = 1 3. n = 2 | II. x = (–1) k  /6 + /6 +  k, k k, k  Z Z 1. k = 0 sin 2  /6 = /6 =  3 / 2 3 / 2 не удовлетворяют О.Д.З. 2. k = 1 sin 2*5  /6 = – /6 = – 3 / 2 3 / 2 удовлетворяют О.Д.З. |
Ответ: х = 






2). 

1 – sin t = 2 cos 2 t
| 1). sin t = –1, t = –  /2 + 2 /2 + 2  k, k k, k  Z; Z; | 2). sin t = 1/2, t = (–1) n  /6 + /6 +  n, n n, n  Z; Z; |
I. t = –  /2 + 2 /2 + 2  k, k k, k  Z; Z; 1. k = 0 t = –  /2 /2 удовлетворяют О.Д.З. | II. t = (–1) n  /6 + /6 +  n, n n, n  Z; Z; 1. n = 0 t =  /6 /6 удовлетворяют О.Д.З. 2. n = 1 t = 5  /6 /6 не удовлетворяют О.Д.З. |
| Ответ: t = –  /2 + 2 /2 + 2  k, k, x = –  /4 + /4 +  k, k, k  Z, Z, | t =  /6 + 2 /6 + 2  n, n, x =  /12 + /12 +  n, n, n  Z. Z. |
3. Отбор корней.
1). tgx + tg2x = tg3x О.Д.З.: х 






| sin3x sinx sin2x = 0 sin3x = 0 x =  n/3, n n/3, n  Z, Z,n = 0, x = 0 уд. | sinx = 0 x =  h, h h, h  Z, Z,h = 0, x = 0 уд. | sin2x = 0 x =  m/2, m m/2, m  Z. Z.m = 0, x = 0 уд. Ответ: x = Видео:Уравнение вида a sin x + b cos x =cСкачать  Уравнения вида acosx bsinx cЧтобы решить тригонометрическое уравнение надо путём тригонометрических преобразований свести его к простейшему тригонометрическому уравнению. Напомним формулы решений простейших тригонометрических уравнений. 1. `sinx=a`. Если `|a|>1`, решений нет. Если `|a| 1`, решений нет. Если `|a| Уравнение распадается на два: 1) `2sinx-1=0`, `sinx=1/2` и `x=(-1)^npi/6+pin,n in Z`. 2) `3cosx+1=0`, `cosx=-1/3` и `x=+- arccos(-1/3)+2pin,n in Z`. Отметим, что в сериях решений 1) и 2) не было бы ошибкой использовать разные буквы (например, `n` и `m`), т. к. идёт перечисление решений. Используя формулу приведения `sin2x=cos(pi/2-2x)`, преобразуем наше уравнение `cos(pi/2-2x)+cos(5x-pi/6)=0` или `2cos((3x+pi/3)/2)*cos((7x-(2pi)/3)/2)=0`. Уравнение распадётся на два: 1) `cos((3x+pi/3)/2)=0`; `(3x+pi/3)/2=pi/2+pin,ninZ`; II. Сведение уравнения к алгебраическому от одного переменного Решить уравнение `4sin^3x=3cos(x+(3pi)/2)`. По формуле приведения `cos(x+(3pi)/2)=sinx`, поэтому уравнение запишется: `4sin^3x=3sinx`. Отметим, что в случае двух уравнений `sinx=+-(sqrt3)/2` мы записали не объединение стандартных формул `(-1)^n(+-pi/3)+pin,ninZ`, а более простую, которая получается, если изобразить решения этих уравнений на тригонометрическом круге (рис. 1). (Две верхние точки – решения уравнения `sinx=(sqrt3)/2`, а две нижние – решения уравнения `sinx=-(sqrt3)/2`). `x=pin,ninz`; `x=+-pi/3+pin,n inZ`. Решить уравнение `cos2x+sin^2x=0,5`. Воспользуемся формулой `cos2x=1-2sin^2x`. Получим: `1-sin^2x=0,5` или `sin^2x=1/2`, `sinx=+-1/sqrt2`. Это уравнение можно решить и пользуясь формулой `sin^2x+(1-cos2x)/2`. Тогда оно преобразуется к виду: `cos2x=0`, `2x=pi/2+pin,ninZ`, или Геометрически множества точек (1) и (2) совпадают (рис. 2). Так что решения тригонометрических уравнений могут быть записаны в разной форме. III. Однородные уравнения (хотя формально эти уравнения можно отнестик предыдущему типу) Решить уравнение `5sin^2x-4sinx*cosx-cos^2x=0`. Это однородное уравнение второго порядка. Так как `cosx!=0` (иначе из нашего уравнения следовало бы, что `sinx=0` что противоречит основному тригонометрическому тождеству `sin^2x+cos^2x=1`), то разделим наше уравнение на `cos^2x`. Получим уравнение `5″tg»^2x-4″tg»x-1=0`. Откуда `»tg»x=1` или `»tg»x=-1/5`. Следовательно, `x=pi/4+pin,ninZ`, или `x=-«arctg»1/5+pin,ninZ`. Решить уравнение `2+3sinxcosx=7sin^2x`. Воспользуемся основным тригонометрическим тождеством `1=sin^2x+cos^2x`. Преобразуем наше уравнение к однородному уравнению второго порядка: `2(sin^2x+cos^2x)+3sinxcosx=7sin^2x` или `5sin^2x-3sinxcosx-2cos^2x=0`. Здесь `cosx!=0` (в противном случае из последнего уравнения следовало бы, что `sinx!=0` что противоречит основному тригонометрическому тождеству). Делим последнее уравнение на `cos^2x`. Получаем уравнение `5″tg»^2x-3″tg»x-2=0`. Откуда `»tg»x=1` или `»tg»x=-2/5`. И значит, `x=pi/4+pin,ninZ`, или `x=-«arctg»2/5+pin,ninZ` Наконец рассмотрим уравнение, сводящееся к однородному третьего порядка. Решить уравнение `sin^3x+13cos^3x-cosx=0`. Перепишем это уравнение так: Это однородное уравнение третьего порядка. Деля его на `cos^3x` (`cosx!=0` для решений нашего уравнения), получим уравнение относительно `»tg»x` Делаем замену: `t=»tg»x`. Алгебраическое уравнение `t^3-t^2+12=0` имеет корень `t=-2` (находится подбором среди целых делителей числа `12`). Далее деля многочлен `t^3-t^2+12` на `(t+12)`, раскладываем левую часть алгебраического уравнения на множители Уравнение `t^2-3t+6=0` не имеет действительных корней, т. к. `D sqrt2` не даёт решений. Число `|1-sqrt3| при `2x+varphi=pi/2+2pin,ninZ`. `max_Rf(x)=-2`, `min_R f(x)=-12`. Рассмотрим теперь более сложные тригонометрические уравнения, в которых надо делать отбор корней. V. Рациональные тригонометрические уравнения Решить уравнение `(cos2x+cosx+1)/(2sinx+sqrt3)=0`. Не будем решать это неравенство, а изобразим на тригонометрическом круге (рис. 3а) точки, не удовлетворяющие ОДЗ. Решаем уравнение `cos2x+cosx+1=0`. Преобразуем его: `(2cos^2x-1)+cosx+1=0`, `2cos^2x+cosx=0`, Изобразим решения уравнения `cosx=0` на тригонометрическом круге (рис. 3б). Они удовлетворяют ОДЗ. Изобразим решения уравнения `cosx=-1/2` на тригонометрическом круге (рис. 3в). Мы видим, что точки `x=-(2pi)/3+2pin,ninZ`, не удовлетворяют ОДЗ, а точки `x=(2pi)/3+2pin,ninZ`, удовлетворяют ОДЗ. Таким образом, Решить уравнение `(sinx)/(sin3x)+(sin5x)/(sinx)=8cosxcos3x`. Умножим уравнение на `sinx*sin3x`. Получим: Преобразуем это уравнение: Ещё раз воспользуемся формулой в правой части последнего уравнения и умножим его на `2`. Получим `(1-cos2x)+(cos2x-cos8x)=2(cos4x-cos8x)` или `1+cos8x-2cos4x=0`. Далее: `1+(2cos^2 4x-1)-2cos4x=0`, `2cos4x(cos4x-1)=0 iff` $$ iff left[beginmathrm4x=1.\ mathrm4x=0.endright.$$ Если `cos4x=1`, то `4x=2pin,x=(pin)/2,ninZ`. 1. Изображаем точки на тригонометрическом круге (рис. 4а). Геометрически их `4` штуки (для `n=0,1,2,3` – далее они повторяются). 2. Изображаем точки которые не удовлетворяют ОДЗ на тригонометрическом круге (4б). Их `6` штук (для `m=0,1,2,3,4,5` – далее они повторяются). Видно, что совпадения точек в `(3)` и `(4)` будут при `x=pin,ninZ`. Эти значения надо исключить из решения, т. е. в ответ пойдут точки С решениями уравнения или `x=pi/8+(pin)/4,ninZ`, можно поступить аналогично, сделав отбор на тригонометрическом круге. Но когда точек–решений на тригонометрическом круге много, и много точек, не входящих в ОДЗ, то удобнее воспользоваться аналитическим способом отбора решений. В данном случае точек — решений на тригонометрическом круге в серии `x=pi/8+(pin)/4,ninZ`, будет `8` штук (различные при `n=0, 1, 2, 3, 4, 5, 6, 7` – далее они повторяются), а точек, не входящих в ОДЗ на тригонометрическом круге `6`. Посмотрим, есть ли совпадения, т. е. существуют ли целые `m` и `n` такие, что `pi/8+(pin)/4=(pim)/3 iff 1/8+n/4=m/3 iff` `iff 3+6n=8m iff 3=2(4m-3n)`. Последнее равенство невозможно, т. к. слева стоит нечётное число, а справа чётное. Отметим, что и для решений уравнения `cos4x=1` отбор можно было сделать аналитически. А именно смотрим, существуют ли целые `m` и `n` такие, что `(pin)/2=(pim)/3 iff 3n=2m`. Видим, что `n` делится на `2`. Тогда `n=2k` и `m=3k,kinZ`. Т. е. из решения уравнения `cos4x=1` надо исключить `x=(pin)/2`, где `n=2k`, т. е. оставить `x=(pin)/2` с `n=2k+1,kinZ`. Но при `n=2k+1` в серии `x=(pin)/2` останутся `x=pi/2(2k+1)=pi/2+pik,kinZ`, что и было нами получено на тригонометрическом круге. Иногда отбор решений предлагается сделать в условии задачи. Видео:Уравнения вида a*sinx+b*cosx=cСкачать  Простейшие тригонометрические уравненияУравнение sinx = a, x- неизвестная переменная, a – некоторое постоянное число. а) Если a>1 или a n arcsina+πn, n Например, решение уравнения sinx = 0,3 записывается в виде: x = (-1) n arcsin0,3+πn, n Уравнение соsx = a, x- неизвестная переменная, a – некоторое постоянное число. а) Если a>1 или a 1, то решений нет. Ответ: решений нет. б) x =(-1) k arcsin(- x =(-1) k +1 в) Так как -2,3>1, то решений нет; Ответ: решений нет. г) x= Ответ: д) tgx = 3.Виды тригонометрических уравнений: 1.Уравнения, в которых можно выполнить замену переменной Такие тригонометрические уравнения можно привести, например, к виду где a,b,c – некоторые действительные числа,a ≠0, f(x)- одна из тригонометрических функций. Например, 4sin 2 x +5 sinx+1 = 0. Обозначим sinx = t, (1)тогда данное уравнение можно записать в виде: 4t 2 +5t +1 = 0, это квадратное уравнение относительно t, найдем его корни. Подставим найденные значения t1 и t2 в равенство (1). Получим простейшие тригонометричкские уравнения sinx =-1,sinx =- 0,25. Решение первого уравнения x= — x =(-1) k+1 arcsin0,25+ Ответ: — Решить уравнение sin 2 x + cosx +1= 0. sin 2 x + cosx +1= 0, заменяя sin 2 x = 1- cos 2 x, получим 1- cos 2 x+ cosx +1= 0, cos 2 x — cosx -2= 0. Обозначим cosx = t, (1)тогда данное уравнение можно записать в виде: t 2 -t -2 = 0, это квадратное уравнение относительно t найдем его корни. Подставим найденные значения t1 и t2 в равенство (1). Получим простейшие тригонометричкские уравнения cosx = -1, cosx = 2. Решение первого уравнения x= Второе уравнение решений не имеет, т.к. 2>1. Ответ: 2.Однородные тригонометрические уравнения. Такие уравнения можно привести к виду a∙sin 2 x+bsinxcosx+ k∙cos 2 x= 0, a,b,k – некоторые действительные числа, a≠0, k≠0. Например, 4sin 2 x +5sinx cosx+cos 2 x = 0.Такие уравнения – однородные уравнения второй степени Чтобы решить такое уравнение, надо: 1. Разделить почленно обе части уравнения на cos 2 x ≠ 0,т.е. 4 2.Выполнить преобразования: 4 3.Решить квадратное уравнение относительно tgx, tgx =t. tgx = -1, tgx = — 0,25. x = arctg(-1)+πk, x = — Ответ: — Решить уравнение 4sin 2 x +sin2x -3 = 0. Заменим в данном уравнении sin2x по формуле двойного аргумента на 2sinxcosx, а 3- на 3sin 2 x +3сos 2 x , т.к. sin 2 x +сos 2 x =1, получим: 4sin 2 x +2sinxcosx-3sin 2 x -3сos 2 x =0, sin 2 x +2sinxcosx-3сos 2 x =0. Последнее уравнение – однородное. Решим его: 1. 2. 3. tgx =t, t 2 +2t — 3= 0. D=16, t1= 1;t2= -2 . x = arctg1+πk, x = Ответ: Для решения однородных уравнений можно использовать следующую таблицу:
3.Уравнение вида asinx+bcosx=c Чтобы решить уравнение такого вида (например,3sinx+4cosx=2), можно 1.Записать его в виде sin(x +t) = sin(x +t) = 2.Решить простейшее тригонометрическое уравнение: sin(x +t) = ( в нашем случае sin(x +t) = x = (-1) k arcsin0,4 – t +πk, 3. Определить t, t = arctgb/a ( в нашем случае t = arctg4/3); 4. Записать ответ: x = (-1) k arcsin0,4 – arctg4/3+πk, Решите уравнение 2sinx +cosx = 1. 1. sin(x +t) = 2. x+t = (-1) k arcsin 4. Для решения уравнения вида
Если левая часть тригонометрического уравнения Для решения тригонометрических уравнений данным способом можно использовать таблицу 5.Некоторые другие виды тригонометрических уравнений а) sin(3x+ а) sin(3x+ Обозначим 3x+ Решим это уравнение относительно х: 3x = — Ответ: — б) sin2x – cosx = 0. Заменим в данном уравнении sin2x по формуле синуса двойного аргумента на 2sinxcosx, получим 2sinxсos + cosx = 0. Затем вынесем cosx за скобки, получим: cosx (2sinx-1) = 0, откуда сosx = 0 или 2sinx -1=0; x = x = Ответ: в) sinx + cosx = 0. Это уравнение можно рассматривать как однородное уравнение первой степени относительно функций синуса и косинуса. Чтобы решить это уравнение : Разделим почленно обе части уравнения на cosx,получим: tgx +1 = 0, tgx = -1 . 3.Решим простейшее уравнение tgx = -1, x= Ответ: 6.Уравнения, решаемые с помощью применения свойств ограниченности тригонометрических функций
Ответ: 2) Ответ: 📺 ВидеоУравнение asinx + bcosx = cСкачать  Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать  10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать  10 класс, 30 урок, Преобразование выражения Asinx + Bcosx к виду Csin(x+t)Скачать  Решение уравнения вида a sin x + b cos x = cСкачать  Решение систем уравнений второго порядка. 8 класс.Скачать  Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать  Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.Скачать  Уравнения вида a sinx + b cosx = c (часть 2)Скачать  Решение тригонометрических неравенств. 10 класс.Скачать  Решение уравнения a*sin^2(x)+b*sin(x)*cos(x)+c*cos^2(x)=0Скачать 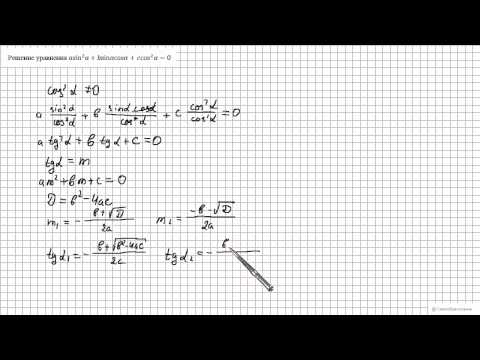 Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать  Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать  Решите уравнение ➜ sinx+cosx=1 ➜ 2 способа решенияСкачать  КАК РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ? // УРАВНЕНИЕ COSX=AСкачать  4 Метода решения уравнений типа: asinx + bcosx = c. #тригонометрия #математика #решениеуравненийСкачать  Решение уравнения a*sinx+b*cosx=0Скачать  Решение тригонометрических уравнений. Метод вспомогательного угла. 10 класс.Скачать  |
 0
0
 sin
sin 





 .
.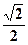 )+
)+  x =(-1) k
x =(-1) k 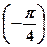 +
+ 
 +
+  , x=
, x=  ;
; , x = arctg
, x = arctg  +
+  Решение второго уравнения
Решение второго уравнения ; (-1) k+1 arcsin0,25+
; (-1) k+1 arcsin0,25+ 
 ,
, ;
; 4tg 2 x +5tgx+1=0.
4tg 2 x +5tgx+1=0. или x = arctg(-0,25)+πn,
или x = arctg(-0,25)+πn,  ,
, ;
; tg2x +2tgx — 3= 0.
tg2x +2tgx — 3= 0. 2. Решить уравнение
2. Решить уравнение 
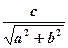 ( в нашем случае sin(x +t) =
( в нашем случае sin(x +t) =  ,
, ).
). , sin(x +t) =
, sin(x +t) =  ;
; , где
, где  можно использовать следующую таблицу:
можно использовать следующую таблицу:
 ,
,  ,
,  .
. содержит лишь одно из выражений
содержит лишь одно из выражений  или
или  и функцию
и функцию 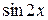 (или произведение
(или произведение  ), то, вводя новую переменную
), то, вводя новую переменную  или
или  и учитывая, что
и учитывая, что  ,
,  , приходим к уравнению относительно
, приходим к уравнению относительно 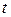 .
.
 +
+  , разделим все члены правой части уравнения на 3, получим x = —
, разделим все члены правой части уравнения на 3, получим x = —  + (-1)k
+ (-1)k  +
+  .
. или sinx = 0,5;
или sinx = 0,5;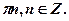



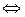

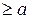

 . Так как
. Так как  и
и  для
для  , то уравнение
, то уравнение 

 Так как
Так как  , то
, то  — корень исходного уравнения.
— корень исходного уравнения.