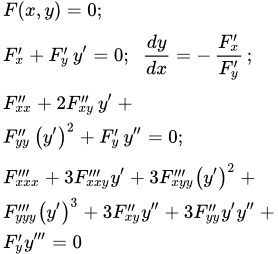- Производная первого порядка
- Доказательство
- Производные высших порядков
- Примеры
- Пример 1
- Решение по формуле 2
- Решение вторым способом
- Пример 2
- Пример 3
- Неявные функции
- Неявные функции, определяемые одним уравнением.
- Неявные функции, определяемые системой уравнений.
- Локальная обратимость регулярного отображения.
- Явные и неявные функции
- 🎬 Видео
Видео:18+ Математика без Ху!ни. Производная неявной функции.Скачать
Производная первого порядка
Пусть функция задана неявным образом с помощью уравнения
(1) .
И пусть это уравнение, при некотором значении , имеет единственное решение . Пусть функция является дифференцируемой функцией в точке , причем
.
Тогда, при этом значении , существует производная , которая определяется по формуле:
(2) .
Доказательство
Для доказательства рассмотрим функцию как сложную функцию от переменной :
.
Применим правило дифференцирования сложной функции и найдем производную по переменной от левой и правой частей уравнения
(3) :
.
Поскольку производная от постоянной равна нулю и , то
(4) ;
.
Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Производные высших порядков
Перепишем уравнение (4), используя другие обозначения:
(4) .
При этом и являются сложными функциями от переменной :
;
.
Зависимость определяет уравнение (1):
(1) .
Поскольку производная правой части уравнения (4) равна нулю, то
(5) .
Подставив сюда производную , получим значение производной второго порядка в неявном виде.
Дифференцируя, аналогичным образом, уравнение (5), мы получим уравнение, содержащее производную третьего порядка :
.
Подставив сюда найденные значения производных первого и второго порядков, найдем значение производной третьего порядка.
Продолжая дифференцирование, можно найти производную любого порядка.
Видео:11. Производная неявной функции примерыСкачать

Примеры
Пример 1
Найдите производную первого порядка от функции, заданной неявно уравнением:
(П1) .
Решение по формуле 2
Находим производную по формуле (2):
(2) .
Перенесем все переменные в левую часть, чтобы уравнение приняло вид .
.
Отсюда .
Находим производную по , считая постоянной.
;
;
;
.
Находим производную по переменной , считая переменную постоянной.
;
;
;
.
По формуле (2) находим:
.
Мы можем упростить результат если заметим, что согласно исходному уравнению (П.1), . Подставим :
.
Умножим числитель и знаменатель на :
.
Решение вторым способом
Решим этот пример вторым способом. Для этого найдем производную по переменной левой и правой частей исходного уравнения (П1).
Подставим (из уравнения (П1)):
.
Умножим на :
.
Пример 2
Найти производную второго порядка от функции , заданной неявно с помощью уравнения:
(П2.1) .
Дифференцируем исходное уравнение, по переменной , считая что является функцией от :
;
.
Применяем формулу производной сложной функции.
.
Дифференцируем исходное уравнение (П2.1):
;
.
Из исходного уравнения (П2.1) следует, что . Подставим :
.
Раскрываем скобки и группируем члены:
;
(П2.2) .
Находим производную первого порядка:
(П2.3) .
Чтобы найти производную второго порядка, дифференцируем уравнение (П2.2).
;
;
;
.
Подставим выражение производной первого порядка (П2.3):
.
Умножим на :
;
.
Отсюда находим производную второго порядка.
Пример 3
Найти производную третьего порядка при от функции , заданной неявно с помощью уравнения:
(П3.1) .
Дифференцируем исходное уравнение по переменной считая, что является функцией от .
;
;
;
;
;
;
(П3.2) ;
Дифференцируем уравнение (П3.2) по переменной .
;
;
;
;
;
(П3.3) .
Из уравнений (П3.2), (П3.3) и (П3.4) находим значения производных при .
;
;
.
Автор: Олег Одинцов . Опубликовано: 16-02-2017
Видео:27. Дифференцирование неявной функции двух переменныхСкачать

Неявные функции
Видео:[Calculus | глава 6] Неявное дифференцирование — что здесь происходит?Скачать
![[Calculus | глава 6] Неявное дифференцирование — что здесь происходит?](https://i.ytimg.com/vi/Vpa7bb6cg4I/0.jpg)
Неявные функции, определяемые одним уравнением.
Пусть функция (F(x,y)) определена в (R^2). Рассмотрим уравнение
$$
F(x,y)=0.label
$$
Множество (G_F) точек плоскости, координаты которых удовлетворяют уравнению eqref, было названо графиком уравнения. Через (A_F) будем обозначать проекцию графика (G_F) на ось (x). Будем рассматривать такие уравнения eqref, графики которых не есть пустые множества.
Так, график уравнения (x^2 + y^2 — 1 = 0) есть окружность, график уравнения ((x-1)(x+y-1)=0) есть пара прямых (x = 1) и (x+y-1=0) (рис. 28.1).
Рис. 28.1
Если график (G_F) уравнения eqref взаимно однозначно проектируется на (A_F), то существует единственная функция (f: ; A_Frightarrow R), график которой совпадает с графиком уравнения. Эта функция каждому (xin A_F) ставит в соответствие тот единственный (y), для которого (F(x,y)=0). Говорят, что уравнение eqref определяет (y) как неявную функцию (x).
Но, как правило, график уравнения eqref не проектируется взаимно однозначно на (A_F). Тогда на (A_F) в общем случае определено бесконечное множество функций, графики которых совпадают с некоторым подмножеством графика (G_F) уравнения eqref. Так, разбивая отрезок ([-1,1]) точками (x_0= -1 Рис. 28.2
Меняя местами переменные (x) и (y), можно говорить о том, что уравнение eqref определяет в некотором прямоугольнике переменную (x) как неявную функцию переменной (y).
Докажем теорему, дающую достаточные условия существования, непрерывности и дифференцируемости неявной функции, определяемой уравнением eqref в некотором прямоугольнике.
- функция (F(x,y)) имеет в окрестности точки ((x_0,y_0)) непрерывные частные производные (F_x(x,y)) и (F_y(x,y));
- (F(x_0,y_0)=0);
- (F_y(x_0,y_0)neq 0).
Тогда существует прямоугольник
$$
K = ,nonumber
$$
в котором уравнение (F(x,y) = 0) определяет (y) как неявную функцию (x). Функция (y=f(x)) непрерывно дифференцируема на интервале ((x_0-a,x_0+a)) и
$$
f'(x)=-frac.label
$$
(circ) Разобьем доказательство на два пункта.
Доказательство существования неявной функции. Из условия (F_y(x_0,y_0)neq 0) следует, что либо (F_y(x_0,y_0) > 0), либо (F_y(x_0,y_0) 0.label
$$
Если (F_y(x_0,y_0) 0).
Так как функция (F_y(x,y)) в точке ((x_0,y_0)) непрерывна и в силу условия eqref принимает в этой точке положительное значение, то найдется такой прямоугольник (рис. 28.3)
$$
K_1=,nonumber
$$
в котором функция (F_y(x,y) > 0).
Рис. 28.3
Рассмотрим функцию одной переменной
$$
psi (y)=F(x_0,y),quad y_0-bleq yleq y_0+b.nonumber
$$
Функция (psi (y)) строго возрастает на отрезке ([y_0-b,y_0+b]), так как
$$
psi'(y)=F_y(x_0,y) > 0.nonumber
$$
Кроме того, в силу условия (F(x_0,y_0)=0)
$$
psi (y_0) = F(x_0,y_0) = 0.nonumber
$$
Поэтому
$$
psi (y_0-b)= F(x_0,y_0-b) 0.label
$$
Неравенства eqref в силу непрерывности функции (F(x,y)) должны сохраняться в некоторых окрестностях точек ((x_0,y_0-b)) и ((x_0,y_0+b)). Поэтому существует такое (ain (0,a_1)), что для всех (xin [x_0-a,x_0+a]) выполнены неравенства
$$
F(x,y_0-b) 0.label
$$
Покажем, что в прямоугольнике
$$
K=,nonumber
$$
уравнение (F(x,y) = 0) определяет (y) как неявную функцию (x).
Возьмем любую точку (x^*in [x_0-a,x_0+a]) и рассмотрим непрерывную на отрезке ([y_0-b,y_0+b]) функцию одной переменной (varphi (y)=F(x^*,y)). В силу условия eqref эта функция принимает на концах отрезка значения разных знаков:
$$
varphi(y_0-b)= F(x^*,y_0-b) 0.nonumber
$$
По теореме Коши о промежуточных значениях найдется такая точка (y^*in [y_0-b,y_0+b]), что
$$
varphi(y^*) = F(x^*,y^*)=0.nonumber
$$
Так как (varphi'(y) = F_y(x^*,y) > 0), то функция (varphi(y)) строго возрастает на отрезке ([y_0-b,y_0+b]) и не может обратиться на этом отрезке в нуль более одного раза.
Таким образом, для любого (xin [x_0-a,x_0+a]) найдется единственный (yin [y_0-b,y_0+b]) такой, что (F(x,y) = 0). Это означает, что в прямоугольнике (K) уравнение (F(x,y) = 0) определяет (y) как неявную функцию (x).
Доказательство непрерывной дифференцируемости неявной функции. Непрерывная на замкнутом прямоугольнике (K) функция (F_y(x,y)) по теореме Вейерштрасса принимает на этом прямоугольнике свое наименьшее значение (alpha). Так как (F_y(x,y) > 0) на (K), то
$$
F_y(x,y)geq a > 0,qquad (x,y)in K.label
$$
Непрерывная на (K) функция (F_x(x,y)) ограничена на (K). Поэтому
$$
|F_x(x,y)| Замечание 1.
Если известно, что уравнение (F(x,y)=0) определяет в прямоугольнике (aleq xleq b, ; cleq yleq d) переменную (y) как неявную функцию (x), то связь между (dy) и (dx) можно установить, формально дифференцируя тождество (F(x,y(x)) = 0). Воспользовавшись инвариантностью формы дифференциала, получаем
$$
F_x(x,y)dx + F_y(x,y)dy = 0.nonumber
$$
Дифференцируя последнее тождество еще раз, можем найти второй дифференциал (d^2y)
$$
F_ dx^2 + 2F_ dx dy + F_ dy^2 + F_y d^2y = 0.nonumber
$$
Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Неявные функции, определяемые системой уравнений.
Рассмотрим систему (m) уравнений с (n+m) неизвестными
$$
left<beginF_1(x_1,ldots,x_n,x_,ldots,x_)=0,\…..\F_m(x_1,ldots,x_n,x_,ldots,x_)=0endright.label
$$
При формулировке общей теоремы о неявных функциях удобно пользоваться понятием декартова произведения множеств. Если (A) и (B) — произвольные множества, то их декартово произведение (Atimes B) есть множество пар ((x,y)), где (xin A), (yin B). Так, декартово произведение ([a,b]times [c,d]) есть множество пар вещественных чисел таких, что (aleq xleq b,) и (cleq yleq d), то есть прямоугольник в (R^2).
Клеточной окрестностью точки (x^0 =(x_1^0,ldots,x_n^0)) будем называть следующее множество:
$$
K(x^0)=<x: ; xin R^n, ; -varepsilon_ileq x_i-x_i^0leq varepsilon_i, ; i=overline>,nonumber
$$
где (varepsilon_i, ; i =overline) — положительные числа, (x = (x_1,…,x_n)).
Легко видеть, что в том случае, когда (K_1(x^0)subset R^n) и (K_2(y^0)subset R^m) — клеточные окрестности, их декартово произведение (K_1(x^0)times K_2(y^0)) есть клеточная окрестность точки ((x^0,y^0)=(x_1^0,…,x_n^0,y_1^0,…,y_m^0) в пространстве (R^).
Для дальнейшего удобно преобразовать переменные, полагая (x=(x_1,…,x_n), ; y=(y_1,…,y_m)), где (y_1=x_,…,y_m=x_).
Тогда систему уравнений eqref можно записать в более кратком виде:
$$
F_i(x,y) = 0, ; i=overline.label
$$
Функции (F_i(x,y) = 0) будем считать определенными в некоторой клеточной окрестности точки ((x^0,y^0)).
Пусть (K(x^0)subset R^n) и (Q(y_0)subset R^m) есть клеточные окрестности. Будем говорить, что система уравнений (F_i(x,y)=0, ; i=overline), определяет в (K(x^0)times Q(y_0)) переменные (y_1,…,y_m) как неявные функции переменных (x_1,…,x_n), если для любого (xin K(x^0)) найдется единственный (yin Q(y^0)) такой, что (F_i(x,y) = 0, ; i=overline).
Пусть выполнены следующие условия:
Тогда найдутся клеточные окрестности (K(x^0) subset R^n) и (Q(y^0) subset R^m) такие, что в (K(x^0)times Q(y^0)) система уравнений eqref определяет переменные (y_1,…,y_m) как неявные функции переменных (x_1,…,x_n). Неявные функции (y_j =varphi_j(x)) непрерывно дифференцируемы в (K(x^0)) и (y_j^0=varphi_j(x^0), ; j=overline).
(circ) Воспользуемся методом индукции по числу уравнений (m). При (m=1) доказательство теоремы 2 не отличается от доказательства теоремы 1 (в дальнейшем будем ссылаться на этот частный случай теоремы 2 как на теорему 1).
Предположим, что утверждение теоремы верно в том случае, когда система eqref содержит (m-1) уравнение. Докажем, что тогда теорема верна и для системы eqref из (m) уравнений.
Так как определитель eqref отличен от нуля, то, раскладывая его по элементам последней строки, получаем, что хотя бы один из соответствующих миноров (m-1)-го порядка отличен от нуля. Пусть, например
$$
<begindisplaystylefrac&…&displaystylefrac<partial y_>\…&…&…\displaystylefrac<partial F_>&…&displaystylefrac<partial F_><partial y_>end>_neq0nonumber
$$
(Здесь и в дальнейшем символ (0) означает, что значение соответствующей функции берется для аргументов с верхним индексом (0)).
Тогда в силу индукции найдутся такие клеточные окрестности
$$
beginK_1=displaystyleleft<(x,y_m): ; vert x_i-x_i^0vertleqvarepsilon_i’, ; i=overline, ; vert y_m-y_m^0vert Замечание 2.
Существует несколько способов доказательства теоремы о неявных функциях. Предложенный способ является, по-видимому, наиболее простым, но обладает двумя недостатками: не дает алгоритма для вычисления неявной функции и не обобщается на бесконечномерный случай.
Видео:Производная неявной функцииСкачать

Локальная обратимость регулярного отображения.
Пусть на множестве (Esubset R^n) заданы (n) функций
$$
f_1(x),…,f_n(x).nonumber
$$
Они задают отображение (f: ; Erightarrow R^n), которое каждой точке (xin E) ставит в соответствие точку (y=f(x)), где
$$
y_1=f_1(x),quad,…,quad y_n=f_n(x).nonumber
$$
Точка (y=f(x)) называется образом точки (x) при отображении (f). Точка (x) называется прообразом точки (y).
Если (Omegasubset E), то множество
$$
f(Omega)=nonumber
$$
называется образом множества (Omega) при отображении (f). Если (omegasubset f(E)), то множество
$$
f^(omega)=nonumber
$$
называется прообразом множества (omega).
Пусть (G subset R^n) есть открытое множество. Отображение (f: ; Grightarrow R^n) называется непрерывным в точке (x^0), если (forall varepsilon > 0 ; existsdelta > 0) такое, что (forall x) таких, что (rho(x,x^0) Лемма 1.
Если (G) есть открытое множество, а (f: ; Grightarrow R^n) — непрерывное отображение, то прообраз каждого открытого множества (omegain f(G)) есть открытое множество.
(circ) Пусть (Omega= f^(omega)). Возьмем любую точку (x^0inOmega). Тогда (f(x^0)=y^0in omega). Так как множество (omega) открыто, то найдется окрестность (S_(y^0)in omega). В силу непрерывности отображения (f) в точке (x^0) найдется шаровая окрестность (S_(x^0)), для которой выполнено условие eqref.
Следовательно,
$$
S_(x^0)subset f^(omega)subsetOmega,nonumber
$$
и (Omega) — открытое множество. (bullet)
Как обычно, под окрестностью (A(x^0)) точки (x^0) будем понимать любое множество (A), для которого точка (x^0) внутренняя.
Пусть (G subset R^n) — открытое множество. Отображение (f: ; Grightarrow R^n) будем называть непрерывно дифференцируемым, если функции (f_1(x),…,f_n(x)), задающие это отображение, непрерывно дифференцируемы в (G). Непрерывно дифференцируемое отображение (f: ; Grightarrow R^n) будем называть регулярным, если в области (G) якобиан отображения (j_f(x)neq 0). Якобианом отображения (j_f(x)) называется следующий функциональный определитель:
$$
j_f(x)=beginfrac&…&frac\…&…&…\frac&…&fracend.nonumber
$$
Пусть (G) — открытое множество в (R^n), а отображение (f: ; Grightarrow R^n) регулярно. Тогда в каждой точке (x^0in G) оно локально регулярно обратимо, то есть (forall x^0in G) найдутся такие окрестности (A(x^0) subset G) и (B(y^0)subset f(G)), где (y^0= f(x^0)), что отображение (f: ; A(x^0)rightarrow B(y^0)) будет взаимно однозначным, причем обратное отображение (f^: ; B(y^0)rightarrow A(x^0)) регулярно.
(circ) Рассмотрим в (Gtimes R^n) систему уравнений
$$
F_i(x,y)equiv y_i-f_i(x)=0,quad i=overline.label
$$
Пусть (x^0) — произвольная точка множества G и (y^0=f(x^0)). Тогда функции (F_i(x,y)) непрерывно дифференцируемы в (Gtimes R^n) и (y_i^0= f_i(x^0), ; i=overline). Так как отображение (f) регулярно, то
$$
<beginfrac&…&frac\…&…&…\frac&…&fracend>_=(-1)^nj_f(x^0)neq0.nonumber
$$
Для системы уравнений eqref выполнены все условия теоремы 2 о неявных функциях. Поэтому найдутся такие клеточные окрестности
$$
beginK(x^0)=left<x: ; vert x_i-x_i^0vertleqvarepsilon_i, ; i=overlineright>,quad K(x^0)subset G,\Q(y^0)=left<y: ; vert y_i-y_i^0vertleqdelta_i, ; i=overlineright>,quad Q(y^0)subset f(G),endnonumber
$$
что в (K(x^0)times Q(y^0)) система уравнений eqref определяет переменные (x_1,…,x_n) как неявные непрерывно дифференцируемые функции переменных (y_1,…,y_n):
$$
beginx_1=varphi_1(y),quad …,quad x_n=varphi_n(y),\xin K(x^0),quad yin Q(y^0),quad x_i^0=varphi_i(y^0),quad i=overline.endlabel
$$
Пусть (B(y^0)) есть внутренность (Q(y^0)):
$$
B(y^0) = left<y: ; |y_i-y_i^0| Следствие.
Если (f: ; Grightarrow R^n) есть регулярное отображение, то образ любого открытого множества (Omegasubset G) есть открытое множество.
(circ) Пусть (omega=f(Omega)). Возьмем произвольную точку (y^0inomega) и пусть (x^0) есть какой-то ее прообраз. Тогда, вследствие теоремы 3, найдутся такие окрестности (A(x^0) subset Omega) и (B(y^0) subset omega); что отображение (f: ; A(x^0)rightarrow B(y^0)) регулярно обратимо. Поэтому каждая точка (y^0inomega) принадлежит (omega) вместе с некоторой окрестностью (B(y^0)). Множество (omega=f(Omega)) открыто. (bullet)
Видео:11.1. Касательная к неявной функции / производная неявной функции ПРИМЕРЫСкачать

Явные и неявные функции
Определение.
Функция называется явной, если она задана формулой, правая часть которой не содержит зависимой переменной.
Такая функция имеет вид: 
Например, 
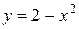

Определение.
Неявной функцией y независимой переменной х называется функция, значения которой находятся из уравнения, связывающего х и y и, не разрешенного относительно y.
Неявная функция имеет вид: 
Например, 

Замечание.
Термины «явная функция» и «неявная функция» характеризуют не природу функции, а способ ее задания.
Основные характеристики функции
Изучить функцию – это значит охарактеризовать ход ее изменения (ее поведение) при изменении независимой переменной. Характеризуют функцию по следующим свойствам:
1) четность или нечетность функции;
2) периодичность функции;
4) возрастание или убывание функции (монотонность функции);
5) ограниченность функции.
Рассмотрим эти характеристики.
Четные и нечетные функции
Определение.
Функция 

Например, 

График четной функции расположен симметрично относительно оси 
 |
Определение.
Функция 

Например, 

График нечетной функции расположен симметрично относительно начала координат (рис.1.5).
Функция может быть ни четной. ни нечетной, и в этом случае её называют функцией общего вида.
Например, 


Графики таких функций не симметричны ни относительно оси 
Периодические функции
Определение.
Функция 


Наименьшее из положительных чисел Т, удовлетворяющих условию определения, называется периодом функции 
Например, функции 


Нули функции
Определение.
Значение аргумента, при котором функция обращается в нуль, 
Например, нулями функции 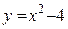


Монотонные функции
Определение.
Функция называется возрастающей (убывающей) в некоторой области изменения аргумента, если большему значению аргумента соответствует большее (меньшее) значение функции (рис.1.6, 1.7).
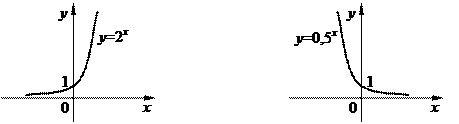 |
Определение.
Если функция в некоторой области изменения аргумента является только возрастающей или только убывающей, то функция называется монотонной.
Ограниченные функции
Определение.
Функция 



Например, функции 




График ограниченной функции лежит между прямыми 

 |
УПРАЖНЕНИЯ
1. Найти область определения следующих функций:
1) 

2) 

3) 

4) 

2. Найти множество значений функции:
1) 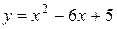

2) 

3) 

3. Найти 




Ответ: 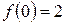


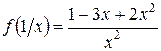
4. Пусть 

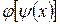

Ответ: 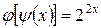

5. Установить чётность или нечётность функции:
1) 
2) 
3) 
4) 
6. Найти основные периоды функций:
1) 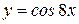

2) 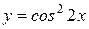
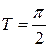
3) 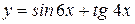

7. Введя промежуточные аргументы, представить данную функцию, как суперпозицию других функций:
1) 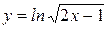


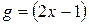
2) 


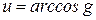


8. Для данных функций найти явные обратные:
1) 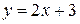

2) 

3) 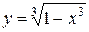
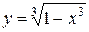
🎬 Видео
19. Производная второго порядка неявной функцииСкачать

Математика без Ху!ни. Уравнение касательной.Скачать

Составить уравнение касательной к графику функции, заданной в неявном видеСкачать

Математика Без Ху!ни. Производная функции, заданной параметрически.Скачать

Как находить производную неявной функции - bezbotvyСкачать

Дифференцирование функции в явном и неявном видеСкачать

Касательная к параметрически и неявно заданной функцииСкачать

Неявные дифференциальные уравнения первого порядкаСкачать

Математический анализ, 31 урок, Дифференцирование сложных и неявных функцийСкачать

Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Производная функции, если функция задана в неявном видеСкачать