Уравнения в изображениях по лапласу

Назначение . Данный сервис предназначен для нахождения онлайн оригинала f(t) по изображению F(p) . Результаты вычисления оформляются в формате Word (см. пример).

• Решение онлайн
• Видеоинструкция

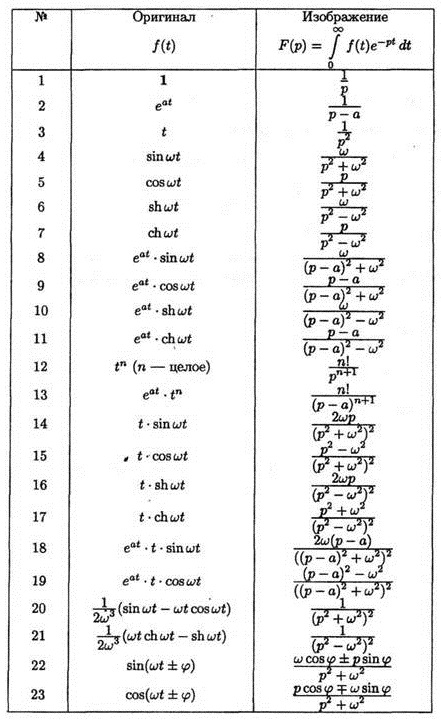
Таблица оригиналов и изображений Лапласа

Изображение	Оригинал
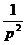	t
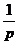	1
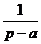	e at
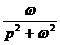	sin(ωt)
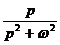	cos(ωt)
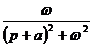	e -at sin(ωt)
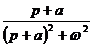	e -at cos(ωt)
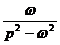	sh(ωt)
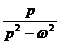	ch(ωt)

Начальной функцией или оригиналом называют функцию f(t) действительной переменной t , удовлетворяющей следующим условиям:

1. f(t)=0 при t 0 и s – некоторые вещественные числа, то |f(t)|≤Me st при t≥0.
2. f(t) — кусочно-непрерывная и интегрируемая на любом конечном отрезке изменения t .

Точная нижняя грань s₀ всех чисел s , для которых выполняется неравенство, называется показателем роста функции f(t) .

Видео:Метод Лапласа решения ДУСкачать

Теоремы запаздывания и смещения

Теорема смещения: L[e p₀t f(t)] = F(p-p₀).
Пример . (p+4)/((p+4) 2 +9) = e -4t cos(3t)

Видео:Преобразование Лапласа по определениюСкачать

Примеры решений задач по операционному исчислению (преобразованию Лапласа)

Операционное (символическое) исчисление – это один из методов математического анализа, позволяющий в некоторых случаях свести исследование и решение дифференциальных, псевдодифференциальных, интегральных уравнений, к более простым алгебраическим задачам.

Изучая преобразование Лапласа, мы вводим оригинал функции $f(t)$ и ее изображение $F(p)$, находимое по формуле:

$$F(p) = int_0^infty f(t) e^dt$$

Для быстроты и удобства решения задач составлена таблица изображений и оригиналов, которая, наряду с теоремами (линейности, подобия, смещения, запаздывания), свойствами и правилами дифференцирования и интегрирования изображения/оригинала, постоянно используется в решении примеров.

В этом разделе вы найдете готовые задания разного типа: восстановление оригинала или изображения функции, нахождение свертки функций, решение ДУ, систем ДУ или интегральных уравнений с помощью преобразования Лапласа и т.д.

Видео:7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

Как найти изображение функции

Задача 1. Найти изображение данного оригинала, или оригинала, удовлетворяющего данному уравнению

Задача 2. Пользуясь определением, найти изображение функции $f(t)=3^t$.

Задача 3. Найти изображение функции: $int_0^t cos tau cdot e^dtau. $

Задача 4. Найти изображение оригинала $f(x)$ двумя способами:
1) Вычислив интеграл $F(p) = int_0^infty f(x) e^dx$;
2) Воспользовавшись таблице изображений и свойствами преобразования Лапласа.
Оригинал задается формулой (курсочно-линейная функция, см. файл).

Видео:Лекция 124. Преобразование Лапласа. ВведениеСкачать

Как найти оригинал функции

Задача 5. Найти оригинал изображения $F(p)$, где

Задача 6. Найти оригинал изображения

Задача 7. Найти оригинал для функции с помощью вычетов

Видео:Неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами МЕТОДОМ ЛАПЛАСАСкачать

Как решить ДУ (систему ДУ) операционным методом

Задача 8. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом

Задача 9. Найти решение задачи Коши методами операционного исчисления

Задача 10. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.

Задача 11. Методом операционного исчисления найти решение задачи Коши для ДУ 3-го порядка

Задача 12. Решите задачу Коши для системы дифференциальных уравнений с помощью преобразования Лапласа.

Задача 13. C помощью формулы Дюамеля найти решение уравнения

Задача 14. Решить систему ДУ с помощью преобразования Лапласа

Видео:Преобразование Лапласа - bezbotvyСкачать

Как решить интегральное уравнение

Задача 15. Методом операционного исчисления найти решение интегрального уравнения

$$ y(t)=cos t +int_0^t (t-tau)^2 y(tau)d tau. $$

Задача 16. Решить интегральное уравнение

$$ int_0^t ch (tau) x(t-tau)d tau = t. $$

Видео:Уравнение Лапласа (ФКП)Скачать

Как найти свертку функций

Задача 17. Найти свертку функций $f(t)=1$ и $phi(t)=sin 5t$.

Видео:Преобразование Лапласа / Примеры изображений простейших функцийСкачать

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.

Видео:Операционное исчисление | Преобразование Лапласа | Решение задачСкачать

Применение преобразования Лапласа к решению
линейных дифференциальных уравнений и систем

Видео:Билет №04 "Потенциал электростатического поля"Скачать

1°. Общие сведения о преобразовании Лапласа: оригинал и изображение

Функцией-оригиналом называется комплекснозначная функция действительного переменного , удовлетворяющая следующим условиям:

2) функция интегрируема на любом конечном интервале оси ;

3) с возрастанием модуль функции растет не быстрее некоторой показательной функции, т. е. существуют числа 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAQBAMAAAC1onFLAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAgUHAYqEh5RGR0VIxELEI83NdAAABBklEQVQY02NgIAAcBRWA5EVBMVRhDjUwdfq/AZCc/kUBVXa6sC2IYjNfwMDANN8AVZKxguExiGYR/sDAwOcvAGK7XIDJsgcw7D8ApFlVfzAwCM0HG8yysAEqe16AQR+kgZ3xEwNbwHqIIMvKBAgDaJY+yLJklt8MfB2foXpYTCHS8gIM+SBZR6aPDFu4P8IsZDI9AJXtB8kGsX3leMD5Ce5aJuMDEFmwyQUMnzkTuD4gZIORZNkMGJYrQkyBmgx2PdDB+hOAzhBgsDdg2C8AleSGuqp9AsP+DQwMXQIMQL/GQ8ORZSnUR5y1DOFA3/7/zyDJsB5IooYG7yvXGoz4aoAzeYQYGADRdjuTYajQpgAAAABJRU5ErkJggg==» /> и такие, что для всех имеем

Изображением функции-оригинала по Лапласу называется функция комплексного переменного , определяемая равенством

при s_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAFIAAAATBAMAAADxBkdhAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAQcCBEFor0KCR6LBxSK9m8wAAAVlJREFUKM9jYCAaJBsbGx8jSqVj71LRWVuIUiqrwMB6iViVDHcT0AQNcaoUQBN0LsVh+3UGBlYlVSAnqUVaFarUASrPuKkFprJQ8JQKA0NUQmwAA0vBpZZciPnOxVClUQmzYSoXW1xyYGC7ycBewMB65DYD7waIOCtUaTHDDQY2EajtQMR8WVD6AgNj6lUGXgWoEawVYKWrpiYw9AglQFSyX2PgvGFsbMDAwHmFQXYDTKUGWOXZuwVsC1gVICqZ7jAw3wHLAl1gGwBVWAkOOja38IvMCowXoCpvMrDdYGAAKvGdwLAKotAV6szYCYzXgCovglQWMHBcZ1OYlcDWABRX4FmG6vVTCcwKTGCVsnfvKrDUWgQwX9oElJvb0ZSAGvJOmzUcOCFmgkP3IBCDDClngxjVipSEGBig7kQGLDexJg2g3zegCfFcxZ6KZoSjJ6FJShOwGwqMIwCRZlRL/vuSSQAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />. Условие 3 обеспечивает существование интеграла (2).

Преобразование (2), ставящее в соответствие оригиналу его изображение , называется преобразованием Лапласа. При этом пишут .

Видео:Найти изображения оригиналов по Лапласу. Операционное исчисление. Функция-оригинал.Скачать

Свойства преобразования Лапласа

Всюду в дальнейшем считаем, что

I. Свойство линейности. Для любых комплексных постоянных и

II. Теорема подобия. Для любого постоянного 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADEAAAAQBAMAAABNQoq8AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcGe2BFbQSGBMfCxcU2qjNsAAADDSURBVBjTY2AgDYgvxCHB5WyyALtM9wW2HUhcDgs4006A8TGyyprjAlCWiwCjCpDNekkzACLQrA6RYnwkwKgHZK42DVFghkq5CcBlAhi4NjOwPSuGGtMJlmJ/xMCgV8DA9JSB6yXc8kg3IMEKkelTAOo2gMv4Iuypm8DA+DoArgVkGiPQbdpgGdY3DDAXQP3DAPKPiAFjkRMbiqsZ1iWwPweGkY+RafYxEL8IJsHA5jklAeSShQysIHtYEaHD2JbKwAAA/gYrl5lLD9QAAAAASUVORK5CYII=» />

III. Дифференцирование оригинала. Если есть оригинал, то

Обобщение: если раз непрерывно дифференцируема на и если есть оригинал, то

IV. Дифференцирование изображения равносильно умножению оригинала на «минус аргумент», т.е.

V. Интегрирование оригинала сводится к делению изображения на

VI. Интегрирование изображения равносильно делению на оригинала:

(предполагаем, что интеграл сходится).

VII. Теорема запаздывания. Для любого положительного числа

VIII. Теорема смещения (умножение оригинала на показательную функцию). Для любого комплексного числа

IX. Теорема умножения (Э. Борель). Произведение двух изображений и также является изображением, причем

Интеграл в правой части (14) называется сверткой функций и и обозначается символом

Теорема XI утверждает, что умножение изображений равносильно свертыванию оригиналов , т.е.

Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать

Отыскание оригиналов дробно-рациональных изображений

Для нахождения оригинала по известному изображению , где есть правильная рациональная дробь, применяют следующие приемы.

1) Эту дробь разлагают на сумму простейших дробей и находят для каждой из них оригинал, пользуясь свойствами I–IX преобразования Лапласа.

2) Находят полюсы этой дроби и их кратности . Тогда оригиналом для будет функция

где сумма берется по всем полюсам функции .

В случае, если все полюсы функции простые, т.е. , последняя формула упрощается и принимает вид

Пример 1. Найти оригинал функции , если

Решение. Первый способ. Представим в виде суммы простейших дробей

и найдем неопределенные коэффициенты . Имеем

Полагая в последнем равенстве последовательно , получаем

Находя оригиналы для каждой из простейших дробей и пользуясь свойствам линейности, получаем

Второй способ. Найдем полюсы функции . Они совпадают с нулями знаменателя . Таким образом, изображение имеет четыре простых полюса . Пользуясь формулой (17), получаем оригинал

Пример 2. Найти оригинал , если .

Решение. Данная дробь имеет полюс кратности и полюс кратности . Пользуясь формулой (16), получаем оригинал

Видео:Преобразование Лапласа и вынужденное движение | Утро с теорией управления, лекция 3Скачать

2°. Решение задачи Коши для линейных дифференциальных уравнений с постоянными коэффициентами

Пусть требуется найти решение дифференциального уравнения второго порядка с постоянными коэффициентами

Будем считать, что функция и решение вместе с его производньь ми до второго порядка включительно являются функциями-оригиналами. Пусть . По правилу дифференцирования оригиналов с учетом (2) имеем

Применяя к обеим частям (1) преобразование Лапласа и пользуясь свойством линейности преобразования, получаем операторное уравнение

Решая уравнение (20), найдем операторное решение

Находя оригинал для , получаем решение уравнения (18), удовлетворяющее начальным условиям (19).

Аналогично можно решить любое уравнение n-го порядка с постоянными коэффициентами и с начальными условиями при .

Пример 3. Решить дифференциальное уравнение операторным методом

Решение. Пусть , тогда по правилу дифференцирования оригинала имеем

Известно, что поэтому, переходя отданной задачи (21)–(22) к операторному уравнению, будем иметь

Легко видеть, что функция удовлетворяет данному уравнению и начальному условию задачи.

Пример 4. Решить уравнение .

Решение. Так как и по условию , то операторное уравнение будет иметь вид

Отсюда находим операторное решение

Разлагаем правую часть на элементарные дроби:

Переходя к оригиналам, получаем искомое решение .

Пример 5. Решить уравнение .

Решение. Так как и по условию , то операторное уравнение будет иметь вид

и, следовательно, операторное решение

Разложим правую часть на элементарные дроби:

Переходя к оригиналам, получим решение поставленной задачи

Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

3°. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами

Пусть требуется найти решение системы двух уравнений с постоянными коэффициентами

удовлетворяющее начальным условиям

Будем предполагать, что функции , а также и являются функциями-оригиналами.

По правилу дифференцирования оригиналов с учетом (24) имеем

Применяя к обеим частям каждого из уравнений системы (23) преобразование Лапласа, получим операторную систему

Эта система является линейной алгебраической системой двух уравнений с двумя неизвестными и . Решая ее, мы найдем и , а затем, переходя к оригиналам, получим решение системы (23), удовлетворяющее начальным условиям (24). Аналогично решаются линейные системы вида

Пример 6. Найти решение системы дифференциальных уравнений операторным методом

удовлетворяющее начальному условию .

Решение. Так как и , то операторная система будет иметь вид

Решая систему, получаем

Разлагаем дроби, стоящие в правых частях, на элементарные:

Переходя к оригиналам, получим искомое решение

🎥 Видео

Преобразование Лапласа Решение системы линейных дифференциальных уравненийСкачать

Преобразование Лапласа: 3D-анимация #дубляжСкачать

Решить задачу Коши для дифференциального уравнения с помощью формулы ДюамеляСкачать