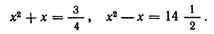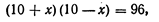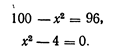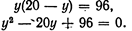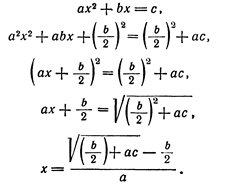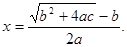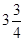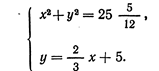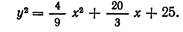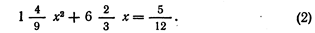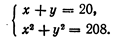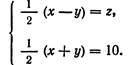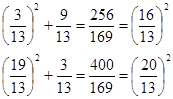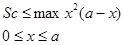| Название: Методы решения уравнений в странах древнего мира Раздел: Рефераты по математике Тип: реферат Добавлен 19:57:57 07 марта 2011 Похожие работы Просмотров: 236 Комментариев: 26 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать |
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения
Ясно, что, выбирая в качестве неизвестного полу разность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).
Квадратные уравнения в Индии.
Задачи на уравнения встречаются уже в астрономическом трактате “Ариабхаттаим”, составленном в 449 г. индийским математиком и астрономом Арибхаттой. Но это уже раннее средневековье.
В Алгебраическом трактате ал-Хорезми даётся классификация линейных и квадратных уравнений.
Индий учёные знали решения неопределённых уравнений в целых числах (в том числе и в отрицательных, чего сам Диофант избегал).
Формула решений квадратного уравнения.
Греческий математик Герон (I или II век нашего летоисчисления) вывел формулу для решения квадратного равнения ax 2 + bx = c умножением всех членов на а и
прибавлением к обеим половинам уравнения 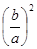
В индии пришли к более простому способу вывода, который встречается в школьных учебниках: они умножали на 4a и к обеим половинам по b 2 . Это даёт:
Индийские математики часто давали задачи в стихах.
Задача о лотосе.
Над озером тихим, с полмеры над водой,
Был виден лотоса цвет.
Он рос одиноко, и ветер волной
Нагнул его в сторону – и уж нет
Цветка над водой.
Нашёл его глаз рыбака
В двух мерах от места, где рос.
Сколько озера здесь вода глубока?
Тебе предложу я вопрос.
Ответ:
Из истории решения системы уравнений, содержащей одно уравнение второй степени и одно линейное
В древневавилонских текстах, написанных в III—II тысячелетиях до н. э., содержится немало задач, решаемых с помощью составления систем уравнений, в которые входят и уравнения второй степени. Вот одна из них.
. “Площади двух своих квадратов я сложил: 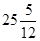
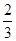
Соответствующая система уравнений в современной записи имеет вид:
Для решения системы (1) вавилонский автор возводит во втором уравнении у в квадрат и согласно формуле квадрата суммы, которая ему, видимо, была известна, получает:
Подставляя это значение у в первое из системы уравнений (1), автор приходит к квадратному уравнению:
Решая это уравнение по правилу, применяемому нами в настоящее время, автор находит х, после чего определяет у. Итак, хотя вавилоняне и не имели алгебраической символики, они решали задачи алгебраическим методом.
Диофант, который не имел обозначений для многих неизвестных, прилагал немало усилий для выбора неизвестного таким образом, чтобы свести решение системы к решению одного уравнения. Вот один пример из его “Арифметики”.
Задача 21. “Найти два числа, зная, что их сумма равна 20, а сумма их квадратов — 208”.
Эту задачу мы решили бы путем составления системы уравнений:
Диофант же, выбирая в качестве неизвестного половину разности искомых чисел, получает (в современных обозначениях):
Складывая эти уравнения, а затем вычитая одно из другого (все это Диофант производит устно), получаем
x = 2 + 10; у = 10 —2.
х 2 + у 2 = (г + lO) 2 + (10 — г) 2 == 2z 2 + 200.
z = 2; х = 2 + 10 = 12; у = 10 — 2 = 8.
Задача Диофанта №80 (Из II книги его “Арифметики”)
Найти 2 таких числа, чтобы сумма квадрата каждого из них с другим искомым числом дала полный квадрат,
Пусть первое число (I) будет s. Чтобы квадрат его •при прибавлении второго числа дал квадрат, второе число должно быть 2s + 1, так как в таком случае выполняется требование задачи: квадрат первого числа. сложенный со вторым, дает
s 2 + 2s + 1, то есть полный квадрат (s + 1) 2 .
Квадрат второго числа, сложенный с первым, должен также дать квадрат, то есть число (2s + I) 2 + s, равное
4s 2 + 5s + 1 == t 2
Положим, что t = 2s — 2; тогда t 2 = 4s 2 — 8s + 4. Это выражение должно равняться 4s 2 + 5s + 1. Итак, должно быть:
4s 2 — 8s + 4 == 4s 2 + 5s + l откуда s=
Значит, задаче удовлетворяют числа:
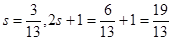
Почему Диофант делает предположение, что t==2s—2, он не объясняет. Во всех своих задачах (в дошедших до нас шести книгах его их 189) он делает то или другое предположение, не давая никакого обоснования.
Вообще содержание 6 книг таково:
В “Арифметике” 189 задач, каждая снабжена одним или несколькими решениями. Задачи ставятся в общем виде, затем берутся конкретные значения входящих в нее величин и даются решения.
Задачи книги I в большинстве определенные. В ней имеются и такие, которые решаются с помощью систем двух уравнений с двумя неизвестными, эквивалентных квадратному уравнению. Для его разрешимости Диофант выдвигает условие, чтобы дискриминант был полным квадратом. Так, задача 30— найти таких два числа, чтобы их разность и произведение были заданными числами,— приводится к системе
Диофант выдвигает “условие формирования”: требуется, чтобы учетверенное произведение чисел, сложенное с квадратом разности их, было квадратом, т. е. 4b + а 2 = с 2 .
В книге II решаются задачи, связанные с неопределенными уравнениями и системами таких уравнений с 2, 3, 4, 5, 6 неизвестными степени не выше второй.
Диофант применяет различные приемы. Пусть необходимо решить неопределенное уравнение второй степени с двумя неизвестными f2 (х, у) ==0. Если у него есть рациональное решение (x0 , y0 ), то Диофант вводит подстановку
в которой k рационально. После этого основное уравнение преобразуется в квадратное относительно t, у которого свободный член f2 ( x0 , у 0 ) = 0. Из уравнения получается t1 == 0 (это значение Диофант отбрасывает), t2 — рациональное число. Тогда подстановка дает рациональные х и у.
В случае, когда задача приводилась к уравнению у 2 = ax 2 + bx + с, очевидно рациональное решение x0 = О,y0 =±C . Подстановка Диофанта выглядит так:
Другим методом при решении задач книги II Диофант пользовался, когда они приводили к уравнению у 2 == = a 2 x 2 + bx + с. Он делал подстановку
после чего х и у выражались рационально через параметр k:
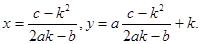
Диофант, по существу, применял теорему, состоящую в том,; что если неопределенное уравнение имеет хотя бы одно рациональное решение, то таких решений будет бесчисленное множество, причем значения х и у могут быть представлены в виде рациональных функций некоторого параметра”
В книге II есть задачи, решаемые с помощью “двойного неравенства”, т. е. системы
Диофант рассматривает случай а = с, но впоследствии пишет, что метод можно применить и при а : с = т 2 , Когда а == с, Диофант почленным вычитанием одного равенства из другого получает и 2 —и 2 = b — d. Затем разность b — d раскладывается на множители b — d = п1 и приравнивает и + v = I, и — v = п, после чего находит
Если задача сводится к системе из двух или трех уравнений второй степени, то Диофант находит такие рациональные выражения неизвестных через одно неизвестное и параметры, при которых все уравнения, кроме одного, обращаются в тождества. Из оставшегося уравнения он выражает основное неизвестное через параметры, а затем находит и другие неизвестные.
Методы, разработанные в книге II, Диофант применяет к более трудным задачам книги III, связанным с системами трех, четырех и большего числа уравнений степени не выше второй. Он, кроме того, до формального решения задач проводит исследования и находит условия, которым должны удовлетворять параметры, чтобы решения существовали.
В книге IV встречаются определенные и неопределенные уравнения третьей и более высоких степеней. Здесь дело обстоит значительно сложнее, потому что, вообще говоря, неизвестные невозможно выразить как рациональные функции одного параметра. Но, как и раньше, если известны одна или две рациональные точки кубической кривой fз (х, у) == 0, то можно найти и другие точки. Диофант при решении задач книги IV применяет новые методы”
Книга V содержит наиболее сложные задачи; некоторые из них решаются с помощью уравнений третьей и четвертой степеней от трех и более неизвестных. Есть и такие, в которых требуется разложить данное целое число на сумму двух, трех или четырех квадратов, причем эти квадраты должны удовлетворить определенным неравенствам.,
При решении задач Диофант дважды рассматривает уравнение Пелля ax 2 + 1 = у 2 .
Задачи книги VI касаются прямоугольных треугольников с рациональными сторонами. К условию х 2 + у 2 == z 2 в них добавляются еще условия относительно площадей, периметров, сторон треугольников.
В книге VI доказывается, что если уравнение ax 2 + b == у 2 имеет хотя бы одно рациональное решение, то их будет бесчисленное множество. Для решения задач книги VI Диофант применяет все употребляемые им способы.
Кстати, в одном из древних рукописных сборников задач в стихах жизнь Диофанта описывается в виде следующей алгебраиче-юй загадки, представляющей надгробную надпись на его могиле
Прах Диофанта гробница покоит; дивись ей—и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком.
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.
Задача-загадка сводится к составлению и решению уравнения:
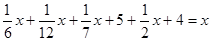
Неопределённое уравнение x 2 + y 2 = z 2
Такое неопределённое уравнение исследовали пиффагорийцы, целые решения которого поэтому называют “пифагоровыми тройками”, они нашли бесконечно много таких троек, имеющих вид:
Более систематическое исследование задач, эквивалентных кубическим уравнениям, относится только к эпохе эллинизма. Архимед в сочинении “О шаре и цилиндре” (книга II, предложение 4) свел задачу о рассечении шара плоскостью на два сегмента, объемы которых имели бы заданное отношение т : п (т > п), к нахождению высоты х большего сегмента из пропорции
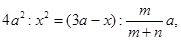
где а — радиус шара.
Архимед обобщает задачу: рассечь заданный отрезок а на две части х и а —х так, чтобы
(а — х) : с = S : х 2 , (2)
где с и S — заданные отрезок и площадь.
Заметив, что при такой общей постановке задача не всегда разрешима (имеются в виду только положительные действительные решения), Архимед приступает к ее исследованию с тем, чтобы наложить ограничения на с и S. Он говорит, что изложит полное решение задачи “в конце”, однако соответствующее место не сохранилось. Жившие на столетие позже Архимеда греческие геометры Диокл и Дионисодор уже не знали его. Они предложили собственные, гораздо более сложные решения, но никто из них не сумел провести анализ общего случая.
Только в VI в. н. э. комментатор Архимеда Евтокий нашел утраченное место. Архимед решает задачу с помощью двух конических сечений:
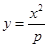
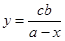
(здесь положено S = pb). Оба уравнения легко получить из пропорции (2). Для выяснения необходимых условий Архимед переходит от пропорции (2) к кубическому уравнению
которое он выражает словесно как соотношение между объемами. Ясно, что уравнение (5) может иметь положительные корни, если
Итак, проблема сводится к нахождению экстремума х 2 (а — х).
Оставим пока в стороне вопрос о методе экстремумов Архимеда, мы вернемся к этому, когда будем говорить об инфинитезимальных методах древних. Скажем только, что Архимед полностью исследовал условия существования положительных вещественных корней уравнения (5), а именно:
1) если Sc 3 /27, то на участке (0, а) имеются два таких корня;
2) если Sc = 4a з /27, то имеется один корень (как сказали бы мы,— двукратный);
3) если Sc > 4a з /27, то корня нет.
Здесь 4а 3 /27 есть максимум х 2 (а — х), достигаемый при х = 2а/3. В конце письма, предпосланного книге “О коноидах и сфероидах” (греки называли сфероидами эллипсоиды вращения, прямоугольными коноидами — параболоиды вращения, а тупоугольными коноидами — полости двуполостных гиперболоидов вращения), Архимед пишет, что с помощью доказанных в книге теорем можно решить ряд задач, как, например: от данного сфероида или коноида отсечь сегмент плоскостью, проведенной параллельно заданной, так, чтобы отсеченный сегмент был равен данному конусу, цилиндру или шару. Перечисленные задачи, так же как и задачи о делении шара, сводятся к кубическим уравнениям, причем в случае тупоугольного коноида уравнение будет иметь вид
Из текста Архимеда можно заключить, что он проанализировал и решил это уравнение. Таким образом, Архимед рассмотрел кубические уравнения вида х 3 + ax + b = 0 при различных значениях a и b и дал метод их решения. Однако исследование кубических уравнений оставалось для греков трудной задачей, с которой, в ее общем виде никто, кроме Архимеда, не мог справиться. Решение отдельных задач, эквивалентных кубическим уравнениям, греческие математики получали с помощью нового геометрического аппарата конических сечений. Этот метод впоследствии восприняли математики стран ислама, которые сделали попытку провести полный анализ всех уравнений третьей степени.
Но еще до этого, и притом греческими математиками, был сделан новый решительный шаг в развитии алгебры: геометрическая оболочка была сброшена, и началось построение буквенной алгебры на основе арифметики. Это произошло в первые века нашей эры.
1. “История математики в древности” Э. Кольман.
2. “Решение уравнений в целых числах” Гельфонд.
3. “В мире уравнений” В.А.Никифоровский.
4. “История математики в школе” Г.И.Глейзер.
5. “Рассказы о старой и новой алгебре” И.Депман.
6. “Пифагор: рассказы о математике” Чистаков.
7. “Краткий очерк истории математики” Стройк Д.Я.
8. “Очерки по истории математики” Болгарский Б.В.
9. “История математики” (энциклопедия) под редакцией Юшкевича.
10. “Энциклопедический словарь юного математика” под редакцией Гнеденко.
- В мире уравнений
- Скачать:
- Предварительный просмотр:
- Презентация «Решение уравнений в Древней Индии, Греции, Китае»
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 💡 Видео
Видео:ИНДИЯ И КИТАЙ В ДРЕВНОСТИ В ОДНОМ ВИДЕО | ИСТОРИЯ ДРЕВНЕГО МИРА, 5 КЛАСССкачать

В мире уравнений
В мире уравнений
СОШ №41 с.Аксаково,
Кто и когда придумал первое уравнение? Ответить на этот вопрос, невозможно.
Теория уравнений интересовала и интересует математиков всех времен и народов. Задачи, сводящиеся к простейшим уравнениям, люди решали на основе здравого смысла с того времени, как они стали людьми. А учебные задачи, которые мы сегодня решаем при помощи уравнений, были хорошо известны еще в Древнем Вавилоне и Древнем Египте, Древнем Китае, Древней Индии и Древней Греции. Выделение алгебры в самостоятельную ветвь математики произошло в арабских странах, куда после распада Римской империи переместился центр научной деятельности. Там появился трактат «Китаб аль-джебр валь-мукабала», в котором были даны общие правила для решения уравнений первой и второй степени. Это сочинение оказало большое значение на развитие математики в Европе, а само слово «аль-джебр», входившее в название книги, постепенно стало названием науки -алгебра –области математики, связанной с искусством решения уравнений.
Выбор темы моего исследования не случаен, т.к. решение уравнений — едва ли не самый распространенный тип экзаменационных задач. На протяжении всех лет обучения в школе мы решаем уравнения, но школьный курс алгебры предусматривает ограниченный набор уравнений. Я умею, без ограничений, решать уравнения первой и второй степени, умею так же решать биквадратные уравнения и особого интереса к ним не проявляю. Интересны уравнения больших степеней. Поэтому объектом моего исследования стали уравнения высших степеней. Цель моей работы заключается в поиске методов решения уравнений произвольных степеней.
Под уравнениями высших степеней понимаются уравнения вида f(х)=0,где f(х)- многочлен степени выше двух. Это может быть кубическое уравнение aх 3 +bх 2 +cх+d=0 или уравнение четвертой степени aх 4 +bх 3 +cх 2 +dх+e=0, или уравнение пятой степени, и так далее. Среди них есть такие, решения которых сводятся, как правило, к квадратному уравнению, либо к определенным формулам Виета, Кардано, Феррари. Наиболее общий прием решения уравнений произвольной степени опирается на теорему Безу или ее следствия.
Таким образом, изучив научно-популярную литературу по данной теме, я выяснила, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции и извлечение корней степени, не превышающей степень уравнения. Более того, все уравнения не выше четвертой степени можно «обслужить» одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни. Общей формулы, применимой ко всем уравнениям пятой степени и выше, не существует. Но имеются специальные вычислительные методы, позволяющие найти корни любого уравнения с любой наперед заданной точностью, ничуть не меньшей, чем дают вычисления по готовым формулам, т.к. в прикладных задачах нас интересуют только приближенные значения корней уравнения, а его разрешимость в радикалах здесь обычно роли не играет.
Настоящая работа будет полезна любознательным школьникам, а так же может служить справочным учебным пособием для выпускников школы. Она позволит улучшить подготовку и математический кругозор в решении уравнений произвольных степеней.
Видео:Индия и Китай в древности Интерактивная картаСкачать

Скачать:
| Вложение | Размер |
|---|---|
| nauchnaya_rabota._drobkova_anya.rar | 2.8 МБ |
Видео:Особенности философии Древней Индии и КитаяСкачать

Предварительный просмотр:
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №41 с. Аксаково
муниципального района Белебеевский район РБ
В мире уравнений
МБОУ СОШ№41 с. Аксаково
Андреева Зинаида Маркеловна
1 Алгебра – наука о решении уравнений 5-6
2 Уравнения высших степеней
2.1 Кубические уравнения 7
2.2 Уравнения четвертой степени 8
2.3 Симметрические уравнения четвертой степени 9
2.4 Уравнения высоких степеней
2.5 Алгебраические уравнения и группы Галуа 10
3 Методы решения уравнений высших степеней
3.1 Разложение многочлена на множители 11
3.2 Метод введения параметра 12
3.3 Метод введения новой переменной
3.4 Комбинирование различных методов 13
3.5 Методы решения симметрических уравнений 3-й и 4-й степеней 14
3.6 Теорема Безу и ее следствия
3.7 Метод Кардано 16
3.8 Метод Феррари 17
3.9Теорема Виета 18-19
Приложение 22 2 Введение
- Важность и актуальность исследования
Кто и когда придумал первое уравнение? Ответить на этот вопрос невозможно. Теория уравнений интересовала и интересует математиков всех времен и народов.
«Можно утверждать, что решение полиномиальных уравнений послужило исторически источником алгебры и что со времен вавилонян, индусов и Диофанта и до наших дней оно остается одной из основных целей» — эти слова французских математиков А. Гротендик (род. 1928) и Ж. Дьедоне (род. 1906), точки зрения которых придерживаются и современные ученые на содержание алгебры.
Выбор темы моего исследования тоже не случаен, так как решение уравнений — самый распространенный тип экзаменационных задач. На протяжении всех лет обучения в школе мы решаем уравнения, но школьный курс алгебры предусматривает ограниченный набор уравнений. Я умею, без ограничений, решать уравнения первой и второй степени и особого интереса к ним не проявляю. Интересны уравнения больших степеней.
Под термином «уравнения высших степеней» понимаются уравнения вида f(x)=0, где f(x)- многочлен степени выше двух. Это может быть кубическое уравнение aх 3 +вх 2 +cх+d=0 или уравнение четвертой степени ах 4 +bх 3 +сх 2 +dх+е=0, или уравнение пятой степени, и так далее. Среди них есть такие уравнения, решения которых сводятся, как правило, к линейным и квадратным по хорошо известным методам. Это разложение на множители многочлена f(х) и введение новой переменной. Но вызвал большой интерес нелинейные уравнения общего вида, решения которых невозможно найти указанными методами. Передо мной встал вопрос: существуют ли другие способы решения уравнений высших степеней? Не попытаться ли, как это делается в математике, отыскать общую формулу, пригодную для решения любых уравнений?
Материал исследования составляют теоретические и практические стороны решения уравнений высших степеней.
Объект исследования- уравнения высших степеней.
Предмет исследования — научно-популярная литература по математике.
3. Цель и задачи исследования
Цель исследования — найти методы решения уравнений высших степеней.
Общая цель исследования определяет конкретные задачи:
-изучить научно-популярную литературу по данной теме;
-выяснить существование специальных методов решения уравнений произвольной степени;
-установить, существует ли формула, выражающая корни любого алгебраического уравнения через конечное число алгебраических операций над его коэффициентами;
-на практике убедиться в правильности данных методов.
4. Практическая значимость исследования.
Материал данного исследования имеет практическую значимость и будет полезна любознательным школьникам, а так же выпускникам школы. Она позволит улучшить подготовку и расширить математический кругозор в решении уравнений произвольных степеней.
5. Методы исследования
Основными методами исследования являются:
1 Алгебра – наука о решении уравнений
Алгебра-часть математики, которая изучает общие свойства действий над различными величинами и решение уравнений, связанных с этими действиями. История алгебры уходит своими корнями в древние времена. Задачи, связанные с уравнениями решались еще в Древнем Египте и Вавилоне. Древние египтяне излагали свои алгебраические познания в числовой форме, не применяли буквенной символики. Путем проб и ошибок числа в условиях задач подбирались так, чтобы получались «хорошие» ответы (натуральные). Других чисел древние египтяне не знали. Более сложные задачи умели решать в Древнем Вавилоне. Там решались уравнения первой, второй и даже отдельные уравнения третьей степени. При этом вавилоняне так же не использовали букв, а излагали решения задач в словесной форме. Способы решения конкретных уравнений дают основание считать, что вавилоняне владели общими правилами нахождения корней уравнений первой и второй степени. Если при решении уравнения надо было извлекать квадратный корень из числа, не являющегося точным квадратом, находили приближенное значение корня. Но эти достижения еще нельзя было назвать наукой, т.к. не было общей теории.
Совсем другой вид приняла алгебра в Древней Греции. Все алгебраические утверждения выражали в геометрической форме. Древнегреческие математики работали не с числами, а с отрезками. Поэтому найти неизвестное для них означало построить отрезок. Большинство задач решалось путем построения циркулем и линейкой, но не все задачи поддавались такому решению. Ведь геометрически можно выразить лишь первые степени (длины), квадраты (площади) и кубы (объемы), но не высшие степени неизвестных. Геометрический путь решения уравнений был гениальной находкой античных математиков, но он сдерживал развитие алгебры. Алгебраические методы, ростки которых возникли в более ранних цивилизациях, в Древней Греции не получили развития.
Выделение алгебры в самостоятельную ветвь математики произошло в арабских странах, куда после распада Римской империи переместился центр научной деятельности. В Багдаде был создан «Дом мудрости», куда по воле халифа собрали образованных людей со всех сторон халифата. Эти мудрецы не только переводили труды своих великих предшественников, но и творили сами. Одним из них был Мухаммед бен Мусса аль- Хорезми. Наиболее значительным его трудом является трактат по алгебре, в котором впервые были разработаны правила преобразования уравнений. Уравнения у него, конечно, были с числовыми коэффициентами и выражались в словесной форме. Но на этих конкретных примерах он показывает способы решения основных типов линейных и квадратных уравнений. В греческих традициях строго геометрически обосновывает свои способы. Любое уравнение должно было быть преобразовано к одному из рассмотренных видов с помощью двух операций: 1) восполнение-перенесение отрицательных членов уравнения в другую часть; 2)противопоставление-приведение подобных членов. Это сочинение, которое по-арабски называется «Китаб аль-джебр вак-мукабала» оказало большое влияние на развитие математики в Европе, а само слово «аль-джебр», входившее в название книги, постепенно стало названием науки – алгебра ( области математики, связанной с искусством решения уравнений).
Итак, решать линейные и квадратные уравнения можно, не записывая каких-либо формул, не зная буквенных обозначений, а только лишь хорошо запомнив многочисленные правила. Но при решении уравнений третьей, четвертой и более высоких степеней без настоящей алгебры двигаться было трудно.
Для математиков, уже умевших — после вавилонян, Евклида и аль — Хорезми –решать линейные и квадратные уравнения, самым желанным было научиться решать уравнения третьей степени (кубические).
2 Уравнения высших степеней
2.1 Кубические уравнения
В 11 веке известный поэт, астроном и математик Омар Хайям без буквенной символики и отрицательных чисел описал все возможные виды уравнений третьей степени и рассмотрел геометрический способ их решения.. Занимался кубическими уравнениями и его современник арабский энциклопедист ал–Бируни. Корни уравнений третьей степени они строили при помощи пересечения парабол, гипербол, окружностей, каким способом решали задачи и греческие геометры. Но арабов, чья математика тяготела к вычислениям, интересовало и численное значение корней. Многие ученые пытались найти правило вычисления корней кубического уравнения, но потерпели неудачу.
Все кубические уравнения являются разновидностями уравнения самого общего вида, т.е. уравнения вида
аx 3 + bx 2 + cx + d =0, где а≠0
Со времен Омара Хайяма ученые средневековья почти 400 лет искали формулу для решения уравнения третьей степени. Были периоды, когда начинало казаться, что сил человеческого ума для решения этой задачи недостаточно. В конце ХV века профессор математики в университетах Рима и Милана Лука Пачоли в своём знаменитом учебнике «Сумма знаний по арифметике, геометрии, отношениям и пропорциональности» задачу о нахождении общего метода решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов Даля Ферро, Никколо Тартальей, Джероламо Кардано вскоре такой метод был найден- выделение полного куба. Д.Кардано написал большую книгу, посвященную алгебре. Главным украшением этой книги и была «формула Кардано», как ее называют теперь. Но формулу Кардано нельзя применять без учета некоторых дополнительных условий и ограничений. Пусть практическое значение этих формул невелико-трудно переоценить тот мощный импульс, который они дали развитию современной алгебры.
Важный вклад в развитии науки внес французский математик Франсуа Виет. Пытаясь решить задачу, каким образом корни уравнения выражаются через коэффициенты, он записал систему равенств. Отыскивая одно, он придумал другое: обозначить буквами не только неизвестные, но и коэффициенты при них. Путем преобразований Ф.Виет доказал, что второй коэффициент данного уравнения приведенного вида равен сумме корней уравнения, взятой с противоположным знаком, третий коэффициент равен сумме попарных произведений корней уравнения, четвертый коэффициент равен сумме всех возможных произведений корней уравнения по три, взятой с противоположным знаком и т.д., свободный член уравнения равен произведению всех корней уравнения, умноженному на (-1) n . Эта связь коэффициентов уравнения приведенного вида с его корнями называется обобщенной теоремой Виета. Она позволяет более легко составлять уравнения по их корням. Хотя буквенная символика Виета обладала некоторыми недостатками, тем не менее это был огромный шаг вперед, до него в математике не было формул. Недаром Виета часто называют «отцом алгебры».
2.2 Уравнения четвертой степени
Метод решения уравнений четвертой степени нашел в ХVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется — метод Феррари.
Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени
x 4 +px 3 +qx 2 +rx+s=0
можно избавиться от члена px 3 подстановкой x=y-p/4. Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
Идея Феррари состояла в том, чтобы представить уравнение в виде А 2 =В 2 , где левая часть- квадрат выражения А=x 2 +s, а правая часть- квадрат линейного выражения В от х, коэффициенты которого зависят от s. После этого останется решить два квадратных уравнения: А=В и А=-В. Конечно, такое представление возможно только при специальном выборе параметра s.
2.3 Симметрические уравнения четвертой степени
Если уравнение имеет вид Р(Q(x))=0, где Р и Q- многочлены, то замена y=Q(x) сводит его решение к решению двух уравнений меньших степеней: Р(y)=0 и Q(x)=y. Замена используется, в частности, при решении биквадратных уравнений.
Более интересный случай- возвратные уравнения, т.е. уравнения четвертой степени
a 2n x 2n +a 2n-1 x 2n-1 +…+a 1 x+a 0 =0,
в которых коэффициенты, одинаково отстоящие от концов, равны: a 2n = a 0, a 2n-1= a 1 и т.д. Такое уравнение сводится к уравнению вдвое меньшей степени делением на x n и последующей заменой y=x±1/x.
При решении возвратных уравнений более высоких степеней обычно используют тот факт, что выражение x k +1/x k при любом k можно представить как многочлен степени k от y=x+1/x.
2.4 Уравнения высоких степеней
Формула корней квадратного уравнения известна с незапамятных времен, а в XVI в. итальянские алгебраисты решили в радикалах уравнения третьей и четвертой степеней. Таким образом, было установлено, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции (сложение, вычитание, умножение, деление) и извлечение корней степени не превышающей степень уравнения. Более того все уравнения данной степени n(n≤4) можно «обслужить» одной общей формулой. При подстановке в нее коэффициентов уравнения получили все корни — и действительные, и комплексные.
После этого естественно возник вопрос: а есть ли похожие общие формулы для решения уравнений пятой степени и выше? Ответ на него смог найти норвежский математик Нильс Хенрик Абель вначале XIX в. Чуть раньше этот результат был указан, но недостаточно обоснован итальянцем Паоло Руффини. Теорема Абеля — Руффини звучит так:
Общее уравнение степени n при n≥5 неразрешимо в радикалах.
Таким образом, общей формулы, применимой ко всем уравнениям данной степени n≥5, не существует.
Хотя уравнения высоких степеней неразрешимо в радикалах, да и формулы Кардано и Феррари для уравнений третьей и четвертой степеней в школе не проходят, в учебниках по алгебре, на вступительных экзаменах в институты иногда встречаются задачи, где требуется решить уравнение выше второй степени. Обычно их специально подбирают так, чтобы корни уравнений можно было найти с помощью некоторых элементарных приемов.
2.5 Алгебраические уравнения и группы Галуа
Теория Галуа позволяет выяснить для любого конкретного уравнения, решается ли оно в радикалах. Для этого данному уравнению сопоставляется некоторая группа перестановок его корней. Важно, что эту группу, названную сейчас группой Галуа, можно определить, не вычисляя корней уравнения, только по его коэффициентам. Галуа установил связь между разрешимостью алгебраического уравнения в радикалах и особым свойством группы этого уравнения, которое также было названо разрешимостью. В частности, любая коммутативная группа разрешима. Если коэффициенты уравнения рациональны и его левая часть не разлагается на множители с рациональными коэффициентами (неприводима), то это уравнение разрешимо в радикалах только тогда, когда разрешима его группа Галуа.
Например, уравнение x 5 — 4x + 2=0 имеет пять различных корней. Хотя они нам неизвестны, можно показать, что группа Галуа данного уравнения совпадает с группой всех перестановок его пяти корней — это самая «большая» из возможных групп для уравнений пятой степени. Доказывается, что эта группа неразрешима. Следовательно, корни данного уравнения не выражаются в радикалах, а значит, общей формулы для решения уравнений пятой степени в радикалах не существует.
3 Методы решения уравнений высших степеней
3.1 Разложение многочлена на множители
При решении алгебраических уравнений часто приходится разлагать многочлен на множители. Разложить многочлен на множители — это значит представить его в виде произведения двух или нескольких многочленов. Некоторые методы разложения многочленов мы употребляем достаточно часто: вынесение общего множителя, применение формул сокращенного умножения, выделение полного квадрата, группировка. Рассмотрим ещё некоторые методы.
Иногда при разложении многочлена на множители бывают полезными следующие утверждения:
- если многочлен a n +a n-1 x+…+a 0 x n ,a 0 ≠0, с целыми коэффициентами имеет рациональный корень х= p/q (где p/q- несократимая дробь, p є Z, q є N), то p- делитель свободного члена a n , а q- делитель старшего коэффициента а 0 ;
- если каким-либо образом подобрать корень х=а многочлена Р n (x) степени n, то многочлен Р n (x) можно представить в виде Р n (х)=(х-а) Р n-1 (х), где Р n-1 (х)- многочлен степени n-1.
Многочлен Р n-1 (х) можно найти либо делением многочлена Р n (х) на двучлен (х-а) «столбиком», либо соответствующей группировку слагаемых многочлена и выделением из них множителя х-а, либо методом неопределенных коэффициентов.
Пример. Разложить на множители многочлен
х 4 -5х 3 +7х 2 -5х+6
Решение. Поскольку коэффициент при х 4 равен 1, то рациональные корни данного многочлена, существуют, являются делителями числа 6, т.е. могут быть целыми числами ±1, ±2, ±3, ±6. Обозначим данный многочлен через Р 4 (х). Так как Р 4 (1)=4 и Р 4 (-4)=23, то числа 1 и -1 не являются корнями многочлена Р А (х). Поскольку Р 4 (2)=0, то х=2 является корнем многочлена Р 4 (х), и, значит, данный многочлен делится на двучлен х-2.
х 4 -5х 3 +7х 2 -5х+6 х-2
х 4 -2х 3 х -3х +х-3
-3х +7х -5х+6
-3х +6х
х -5х+6
х -2х
-3х+6
Следовательно, Р 4 (х)= (х-2)( х -3х +х-3). Так как х -3х +х-3 =
= х 2 (х-3)+(х-3)= (х-3)(х 2 +1), то х 4 -5х 3 +7х 2 -5х+6=(х-2)(х-3)(х 2 +1).
3.2 Метод введения параметра
Иногда при разложении многочлена на множители помогает метод введения параметра. Суть этого метода можно пояснить на следующем примере.
Пример. х 3 -(√3+1)х 2 +3.
Решение : рассмотрим многочлен с параметром а:
который при а=√3 превращается в заданный многочлен. Запишем этот многочлен как квадратный трехчлен относительно а:
а 3 -ах 2 +(х 3 -х 2 ).
Так как корни этого квадратного относительно а трехчлена есть а 1 =х и а 2 =х 2 -х, то справедливо равенство а 2 -ах 2 +(х 3 -х 2 ) = (а-х)(а-х 2 +х). Следовательно, многочлен х 3 -(√3+1)х 2 +3 разлагается на множители √3-х и √3-х 2 +х, т.е.
х 3 -(√3+1)х 2 +3=(√3-х)( х 2 -х-√3).
3.3 Метод введения новой переменной
В некоторых случаях путем замены выражения f(х), входящего в многочлен через у можно получить многочлен относительно у, который уже легко разложить на множители. Затем после замены у на f(х) получаем разложение на множители многочлена Р n (х).
Пример: разложить на множители многочлен
Решение : преобразуем данный многочлен следующим образом:
(х+1)(х+2)(х+3)-15= = (х 2 +3х)( х 2 +3х+2)-15.
Обозначим х 2 +3х через у. тогда имеем
х(х+1)(х+2)(х+3)-15=( х 2 +3х+5)( х 2 +3х-3).
Пример: разложить на множители многочлен (х-4) 4 +(х+2) 4
Решение : обозначим = х-1 через у.
Тогда (х-4) 4 +(х+2) 4 =(у-3) 4 +(у+3) 4 =у 4 -12у 3 +54у 3 -108у+81+у 4 +12у 3 +54у 3 +108у+81=
=2у 4 +108у 2 +162=2(у 4 +54у 2 +81)=2((у 2 +27) 2 -648)=2(у 2 +27-√648)(у 2 +27+√684)=
=2((х-1) 2 +27-√684)((х-1) 2 +27+√684)=2(х 2 -2х+28-18√2)( х 2 -2х+28+18√2).
3.4 Комбинирование различных методов
Часто при разложении многочлена на множители приходится применять последовательно несколько из рассмотренных выше методов.
Пример: разложить на множители многочлен
Решение : Применяя группировку, перепишем многочлен в виде
х 4 -3х 2 +4х-3=( х 4 -2х 2 )-(х 2 -4х+3).
Применяя к первой скобке метод выделения полного квадрата, имеем:
х 4 -3х 2 +4х-3=(х 4 -2∙1∙х 2 +1)(х 2 -4х+4).
Применяя формулу полного квадрата, можно теперь записать, что:
х 4 -3х 2 +4х-3=(х 2 -1) 2 -(х-2) 2 .
Наконец, применяя формулу разности квадратов, получим, что:
х 4 -3х 2 +4х-3=( х 2 -1+х-2)( х 2 -1-х+2)=( х 2 +х-3)(х 2 -х+1).
3.5 Решение симметрических уравнений третьей и четвертой степеней
а) решение симметрических уравнений третьей степени.
Пример: решить уравнение 3х 3 +4х 2 +4х+3=0.
Решение : это уравнение является симметрическим уравнением третьей степени.
Поскольку 3х 3 +4х 2 +4х+3=3(х 3 +1)+4х(х+1)=(х+1)(3х 2 -3х+3+4х)=
=(х+1)(3х 2 +х+3), то данное уравнение равносильно совокупности уравнений
Решение первого из этих уравнений есть х= -1, второе уравнение решений не имеет.
б) решение симметрических уравнений четвертой степени.
Пример: решить уравнение х 4 -5х 3 +8х 2 -5х+1=0.
Решение : Данное уравнение является симметрическим уравнением четвертой степени. Так как х=0 не является его корнем, то, разделив данное уравнение на х 2 , получим равносильное ему уравнение:
х 2 -5х+8-5/х+1/х 2 =0
Сгруппировав слагаемые, перепишем уравнение в виде
х 2 +1/х 2 -5(х+1/х)+8=0
Заменив х+1/х на у, получим уравнение
имеющее два корня у 1 =2 и у 2 =3. Следовательно, исходное уравнение равносильно совокупности уравнений х+1/х=2 и х+1/х=3.
Решение первого уравнения этой совокупности есть х =1, а решение второго есть х и х 3 = .
Следовательно, исходное уравнение имеет три корня: х , х , х 3.
3. 6 Теорема Безу и ее следствия.
Наиболее общий прием решения уравнений высших степеней опирается на теорему Безу и ее следствия. Рассмотрим эту теорему и её следствия.
Пусть имеем многочлен М(х)=а 0 х n +а 1 х n-1 +…+a n , целый относительно х, т.е. многочлен с целыми неотрицательными показателями х, х-а- двучлен. Тогда теорема Безу утверждает:
Остаток от деления многочлена, целого относительно х, на двучлен х-а равен значению многочлена при х=а.
Если разделить многочлен М(х) на х-а, то в частности получится многочлен Q(x), степень которого на 1 меньше степени многочлена М(х), и некоторый остаток R. Очевидно, что остаток R не содержит х, т.е равен постоянному числу, так как степень остатка меньше степени делителя.
Тогда М(х)=(х-а)Q(х)+R. Это равенство верно при любом значении х. Оно является тождеством. Положим в нем х=а. Получим:
т.е М(а)=R, R= М(а). Теорема доказана.
Значение а, при котором R=0, называется корнем многочлена М(х). Оно является и корнем уравнения М(х)=0, так как М(а)=0.
Основная теорема алгебры утверждает, что любой многочлен с числовыми коэффициентами, целый относительно х, имеет по крайней мере один корень х 1 . Из теоремы Безу в этом случае следует, что М(х)=(х- х 1 ) Q(x),где степень многочлена Q(x) на 1 меньше степени многочлена М(х). Заменим в уравнении М(х)=0 левую часть произведения (х- х 1 ) Q(x). Получим (х- х 1 ) Q(x)=0. Приравнивая к нулю множитель х- х 1 , получим уже найденный корень х 1 . Приравняем к нулю второй множитель Q(x)=0. Рассуждая аналогично предыдущему, получим, что последнее уравнение имеет хоть один корень х 2 . Тогда левую часть уравнения Q(x)=0 можно заменить произведением (х-х 2 )Q 1 (х)=0, где Q 1 (х)-многочлен степени n-2. Продолжая рассуждать дальше, убеждаемся, что уравнение n-й степени имеет ровно n действительных или мнимых корней.
Если все коэффициенты в уравнении — действительные числа, то каждый мнимый корень уравнения обязательно имеет сопряженный ему корень этого уравнения, т.е. если уравнение с действительными коэффициентами имеет корень х 1 =а+bi, то оно имеет и корень х 2 =а-bi.
Пример: решить уравнение х 4 -3х 3 -8х 2 +12х+16=0.
Решение : выписываем делители свободного члена 16:
При х=1 в левой части уравнения получим 1-3-8+12+16≠0. Единица не является корнем уравнения.
Проверим х=-1. Левая часть уравнения будет равна 1+3-8-12+16=0, х 1 = -1-корень уравнения.
Делим левую часть уравнения на х-х 1 =х+1:
х 4 -3х 3 -8х 2 +12х+16 х+1
± х 4 ± х 3 х 3 -4х 2 -4х+16
±4 х 3 ±4х 2
±4х 2 ±4х
16х+16
Приравниваем к нулю полученное частное:
Проверяем, является ли х=2 корнем этого уравнения:
8-16-8+16=0, т.е. х 2 =2 – корень этого уравнения.
3.7 Метод Кордано
Данным методом решаются лишь уравнения вида х 3 + рх + q = 0
Используем формулу куба суммы: (a + b) 3 = a 3 + 3a 2 b + b 3 = a 3 + b 3 + 3ab·(a + b)
Заменим (а + b) на х:
х 3 – 3abx – (a 3 – b 3 ) = 0
Исходное уравнение равносильно системе уравнений:
Эту систему можно решать по-разному, но результат один:
Это и есть формула Кардано , часто использующаяся при решении кубических уравнений, когда обычные методы не помогают.
Пример. Решим уравнение х 3 + 15х + 124 = 0
Решение. Имеем p = 15, q = 124.
3.8 Метод Феррари
х 4 + dx 3 + ax 2 + bx + c = 0
Избавляемся от dx 3 подстановкой
х 4 + ах 2 + bx + с = 0.
Идея в том, чтобы представить уравнение в виде А 2 =В 2 , где А = х 2 + s, а В – линейная функция от х. Тогда останется решить уравнение А = ± В.
Возьмем Тогда, учитывая исходное равенство, получим:
Пусть t 0 – корень последнего уравнения. Тогда при t = t 0 правая часть-квадрат:
Решив эту систему, мы найдем решение исходного уравнения.
Это и есть метод Феррари.
Пример. х 4 + 8х 3 + 11 = 68х
Решение . Добавив к обеим частям уравнения 16х 2 и перенеся свободный член вправо, перепишем уравнение следующим образом:
(х 2 +4х) 2 =16х 2 +68х-11
Введем неизвестное t и добавим к обеим частям уравнения выражение t 2 -2(х 2 +4х)t.
( х 2 + 4х – t) 2 = ( 16 — 2t)х + ( 68 — 8t)х — ( 11 – t 2 ).
Левая часть уравнения является квадратом. Найдем такое значение t, при котором квадратный трехчлен от х, стоящий в правой части, тоже является полным квадратом. Для этого нужно, чтобы дискриминант квадратного трехчлена равнялся нулю, т.е. чтобы выполнялось равенство
( 34 — 4t) 2 + (16 — 2t) (1 1 – t 2 ) = 0.
Раскрыв в нем скобки, придем к кубическому уравнению
t 3 – 147t + 666 = 0, где t = 6 –корень уравнения.
При t = 6 исходное уравнение принимает вид:
( х 2 + 4х – 6 ) 2 = ( 2х + 5 ) 2 .
Значит, х 2 + 4х – 6 = ±(2х + 5).
Решая оба получившихся уравнения, найдем четыре корня данного уравнения:
3.9 Теорема Виета
х 3 + px 2 + qx + r = 0
Если х 1 , х 2 , х 3 – корни уравнения, то его можно записать в виде
(х – х 1 )·(х – х 2 )·(х – х 3 ) = 0
Преобразуем, раскрыв скобки:
х 3 – (х 1 + х 2 + х 3 )х 2 + (х 1 х 2 + х 1 х 3 + х 2 х 3 )х – х 1 х 2 х 3 = 0
Имеем возможность вместо одного уравнения третьей степени записать такую систему из трех уравнений:
Видео:УРАВНЕНИЯ В ДРЕВНЕЙ ГРЕЦИИ | ИСТОРИЯ МАТЕМАТИКИСкачать

Презентация «Решение уравнений в Древней Индии, Греции, Китае»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
Колобова Татьяна Евгеньевна, учащаяся 8 > класса Руководитель: Рыбакова Наталья Александровна г. Арзамас 2017
Математика – древний, важный и сложный компонент культуры человека. Она появилась из необходимости практической деятельности человека. Изучая историю математики, мы знакомимся с благородными идеями многих поколений. Мне приходиться делить время между политикой и уравнениями. Однако уравнения гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно. А. Эйнштейн
Математика древних греков удивляет в первую очередь богатством своего содержания Древняя Греция
Диофантовы уравнения Диофант Александрийский Математик Древней Греции. Некоторые называют его «отцом алгебры ». Создатель «Арифметики», которая состоит из 13 книг. Пример: 1) 5x + 35y=40 Решение: Наибольший общий делитель (5, 35) = 5, 40 можно поделить на 5, значит, у этого уравнения есть корни, Например: x=1, y=1
Решение квадратных уравнений с помощью геометрии x 2 В древние времена, когда геометрия была более изучаема, чем алгебра, математики Древней Греции решали уравнение вот так: x² + 4x — 21 = 0 x² + 4x = 21, или x² + 4x +4=21+4 Решение: Выражения x² + 4x +4 и 21+4 геометрически представляют тот же самый квадрат, а исходное уравнение x² +4x –21 +4 –4 = 0 – одинаковые уравнения. Получается, что x + 2 = ±5, или х1 = 3 х2 = -7
Творчество математиков Индии значительно повлияло на развитие арифметики, алгебры и тригонометрии Индийские математики Брахмагупта Ариабхата Древняя Индия
Математики Индии в отличие от греческих математиков вывели более простую формулу решения квадратных уравнений. Она встречается в школьных учебниках. Но, не все индийские математики решали именно по этой формуле. Например, Бхаскара решал квадратные уравнения вот так: x2 — 44х + 484 = -684 + 1008, (х — 22)2 = 324, х — 22= ±18, x1 = 4, x2 = 40. Формула корней квадратного уравнения
Магавира при решении систем линейных уравнений использовал метод, который не отличается от метода уравнивания коэффициентов. Например: 6x -3y =3 5x +4y =22 1) НОК (3;4) =12, 6x -3y =3 *4 24x -12y =12 5x +4y =22 *3 15x +12y =66 2) + 24x -12y =12 15x +12y =66 39x =78 3) 6*2 -3y =3 x= 2 y=3 Ответ: x=2, y=3 Линейные уравнения
Самые заметные научные открытия китайских учёных: метод численного решения уравнений n -степени (метод Руффини – Горнера); теоретико-числовые задачи на системы сравнений первой степени с одним неизвестным (сравнения Гаусса); метод решения систем линейных уравнений (метод Гаусса); вычисление числа π (пи) Древний Китай
Пример: (y +4)2=y2 +202 Решение китайских учёных предположительно такое: (y +4)2=y2 +202 , y2+8y+16= y2 +400, 8y=384, y=48, Ответ: y=48 Решение уравнений
В ходе работы я узнала много нового и полезного из области математики. Познакомилась с биографией великих математиков. Узнала, каким методом решали уравнения древнегреческие, индийские и китайские математики. Составила и решила уравнения новыми для меня способами. Литература БерезкинаЭ. И. Математика древнего Китая. М.: Наука, 1980 Депман И.Я. История арифметики. — М.: Просвещение, 1965. — 415 с. Панов В. Ф. Математика древняя и юная/ Под ред. В. С. Зарубина. — 2-е изд. —М.: Изд-во МГТУ им. Н. Э. Баумана, 2006. —648 с. Рыбников К.А. Возникновение и развитие математической науки. — М.: Изд-во «Просвещение», 1987. — 159 с. Стройк Д. Я. Краткий очерк истории математики. Пер. с нем.—5- изд., испр.— М.: Наука. Гл. ред. физ.мат. лит., 1990.— 256 с
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 945 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 687 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 315 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Кратко о философии Древнего КитаяСкачать

Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 590 687 материалов в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 15.04.2018
- 964
- 1
- 15.04.2018
- 566
- 7
- 15.04.2018
- 2502
- 52
- 15.04.2018
- 587
- 3
- 15.04.2018
- 366
- 5
- 15.04.2018
- 1006
- 11
- 15.04.2018
- 361
- 1
- 15.04.2018
- 295
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 15.04.2018 7822
- PPTX 3.8 мбайт
- 63 скачивания
- Рейтинг: 1 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Рыбакова Наталья Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 10 месяцев
- Подписчики: 2
- Всего просмотров: 17834
- Всего материалов: 11
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Медицина в древних цивилизациях: Древний Египет, Древняя Индия, Древний Китай, АнтичностьСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Ленобласть распределит в школы прибывающих из Донбасса детей
Время чтения: 1 минута
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Каждый второй ребенок в школе подвергался психической агрессии
Время чтения: 3 минуты
В Ленобласти школьники 5-11-х классов вернутся к очному обучению с 21 февраля
Время чтения: 1 минута
В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
💡 Видео
МАТЕМАТИКА ДРЕВНЕГО КИТАЯ И ИНДИИ | История математикиСкачать

5 класс. История. Древняя Индия и КитайСкачать

Древний Китай | Всемирная история 5 класс #15 | ИнфоурокСкачать

2.2 Философия Древнего Китая - Философия для бакалавровСкачать

Древний Китай. Урок по истории для 5 классаСкачать

История Древнего мира: Китай, Египет, Рим, Месопотамия | Лекция для сна | Всемирная история | УмскулСкачать

2.1 Философия Древней Индии - Философия для бакалавровСкачать

Древняя история Индии – это откровенный вымысел.Скачать

История 5 класс (Урок№14 - Китай в древности.)Скачать

5 самых необычных сексуальных традиций Древней Индии!Скачать

Индия и Китай в XVIII веке. Видеоурок 14. История 8 классСкачать

Древняя Индия | История Древнего мира, 5 классСкачать

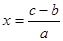
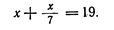
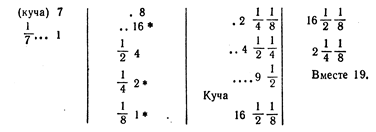
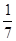 ее часть есть 1. Это записано в первом столбце.
ее часть есть 1. Это записано в первом столбце.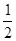 от 8, получает 4. Так как это больше нехватки 3, то на
от 8, получает 4. Так как это больше нехватки 3, то на 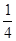 от 8 есть 2,
от 8 есть 2, 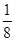 от восьми 1. Ахмес видит, что
от восьми 1. Ахмес видит, что 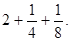
 , удвоенное это число:
, удвоенное это число: 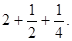 и учетверенное:
и учетверенное: 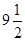 . Сумма этих трех чисел, равная числу
. Сумма этих трех чисел, равная числу 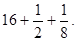 , есть произведение первоначального предположения 7 на
, есть произведение первоначального предположения 7 на 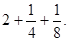 .
.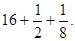 .
.