- WolframAlpha по-русски
- Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha
- Новое в Wolfram Language | Аналитическое решение уравнений в частных производных
- Иллюстрированный самоучитель по Mathematica 3/4
- Дифференциальные уравнения. Решение дифференциальных уравнений в символьном виде.
- Уравнения в частных производных wolfram mathematica
- Основные операции
- Знаки сравнения
- Логические символы
- Основные константы
- Основные функции
- Решение уравнений
- Решение неравенств
- Решение различных систем уравнений, неравенств и уравнений
- Математический анализ
- Пределы
- Производные
- Интегралы
- Дифференциальные уравнения и их системы
- Ошибки при работе с системой
- Использование Wolfram Mathematica в решении дифференциальных уравнений
- Аннотация
- Ключевые слова
- Текст научной работы
- Читайте также
- Математическая подготовка студентов в вузе в контексте будущей профессиональной деятельности
- Использование прикладных программ при изучении математической статистики
- Применение систем компьютерной математики при изучении комплексного анализа
- Организация самостоятельной работы студентов в условиях информационно-образовательной среды вуза
- Системы компьютерной математики в решении дифференциальных уравнений
- Список литературы
- Цитировать
- Поделиться
Видео:Новое в Wolfram Language | Аналитическое решение уравнений в частных производныхСкачать

WolframAlpha по-русски
Математика с WolframAlpha ® . Объяснения с примерами.
Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha
Решение дифференциальных уравнений с выводом результатов в пошаговом представлении (функция «Show steps» — Показать шаги) является одной из важных особенностей Wolfram|Alpha.
Wolfram|Alpha в большинстве случаев может помочь в решении дифференциальных уравнений различного уровня сложности, начиная от простейших дифференциальных уравнений первого порядка с разделяющимися переменными (separable equations ) и включая более сложные уравнения, для решения которых служат, например, методы операционного исчисления, использующие преобразование Лапласа.
Как видим, Wolfram|Alpha сначала определяет (классифицирует) этот пример, как обыкновенное линейное дифференциальное уравнение первого порядка, затем выводит общее решение данного уравнения, график частного решения, удовлетворяющего условию y(1)=1, а также семейство интегральных кривых данного уравнения.
Чтобы получить детальное пошаговое решение, используйте кнопку «Show steps»:
Видео:Новое в Wolfram Language | Аналитическое решение уравнений в частных производных | Колебание струныСкачать

Новое в Wolfram Language | Аналитическое решение уравнений в частных производных
Перевод поста Devendra Kapadia «New in the Wolfram Language: Symbolic PDEs».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации. Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях. Цель этой статьи — приоткрыть завесу в мир УрЧП (тем кто еще с ним не знаком) и ознакомить читателя с тем, как можно эффективно решать УрЧП в Wolfram Language, используя новый функционал для решения краевых задач в DSolve, а так же новую функцию DEigensystem, которая появилась в версии 10.3.
История УрЧП восходит к работам известных математиков восемнадцатого века — Эйлера, Даламбера, Лапласа, однако развитие этой области в последние три столетия так и не остановилось. И потому в статье я приведу как классические, так и современные примеры УрЧП, что позволит рассмотреть эту область знаний под разными углами.
Давайте начнем с рассмотрения колебаний натянутой струны с длиной π, закрепленной на обоих концах. Колебания струны можно смоделировать с помощью одномерного волнового уравнения, приведённого ниже. Здесь u(x,t) — вертикальное смещение точки струны с координатой х в момент времени t:
Затем мы задаём граничные условия, указав тем самым, что концы струны при колебаниях сохраняют свои положения.
Зададим теперь начальные условия для движения струны, указав смещения и скорости различных точек струны в момент времени t=0:
Теперь мы можем использовать DSolve для решения волнового уравнения с начальными и краевыми условиями:
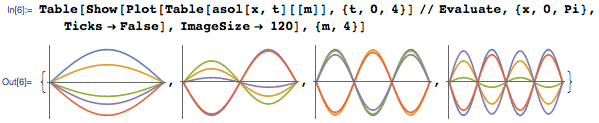
Как указано выше, решение есть бесконечная сумма тригонометрических функций. Сумма возвращается в невычисленной форме (Inactive), поскольку каждый отдельный член разложения имеет физическую интерпретацию, и зачастую даже небольшое количество членов может являться хорошим приближением. К примеру, мы можем взять первые четыре члена для получения приближенного решения asol(x,t)
Каждый член в сумме представляет собой стоячую волну, которые могут быть представлены следующим образом:
И все эти стоячие волны складываются воедино, образуя гладкую кривую, как показано на анимации ниже:
Волновое уравнение относится к классу линейных гиперболических уравнений в частных производных, описывающих распространение сигналов с конечными скоростями. Это УрЧП представляет собой удобный способ для моделирования колебаний в струне или в каком-то другом деформирумом теле, однако ещё более важную роль оно играет в современной физике и инженерных приложениях, т.к. оно описывает распространение света и электромагнитных волн.
Давайте теперь смоделируем поток тепла в стержне единичной длины, изолированном с обоих концов, с помощью представленного ниже уравнения теплопроводности:
Поскольку стержень изолирован с обоих концов, то через них проходит нулевой поток тепла, что можно выразить как граничные условия вида х = 0 и х = 1:
Теперь нужно указать начальное температурное распределение в стержне. В этом примере мы будем использовать приведённую ниже линейную функцию. В левом конце (х = 0) начальная температура — 20 градусов, в правом (х = 1) — 100:
И теперь мы можем решить уравнение теплопроводности с заданными условиями:
Как и в приведённом выше примере с волновым уравнением, мы можем извлечь несколько членов суммы и получить приближенное решение:
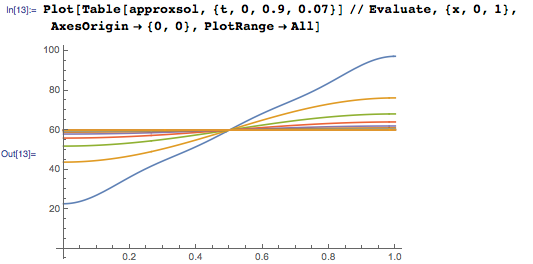
Первый член приближенного решения — 60 — среднее от температур на границах стержня, и она является стационарной температурой для этого стержня. Как показано на графике функции температуры от длины, представленном ниже, температура стержня быстро достигает стационарного значения в 60 градусов:
Уравнение теплопроводности относится к классу линейных параболических уравнений в частных производных, которые описывают процессы диффузии. Это простое на вид уравнение часто можно встретить в самых различных, а иногда и весьма неожиданных областях. Далее в статье мы рассмотрим два примера этого явления.
Рассмотрим теперь уравнение Лапласа, которое используется для моделирования стационарного состояния систем, т. е. поведения после некоторых зависящих от времени уже законченных переходных процессов. В двумерном случае это уравнение можно представить следующим образом:
Ограничим координаты х и у прямоугольной областью Ω, как показано ниже:
Классическая задача Дирихле — найти функцию u(x,y), удовлетворяющую уравнению Лапласа внутри области Ω с заданным условием Дирихле (DirichletCondition), которое определяет значения на границах области Ω, как показано ниже:
Задачу Дирихле можно решить с помощью функции DSolve, весьма изящно задав при этом область:
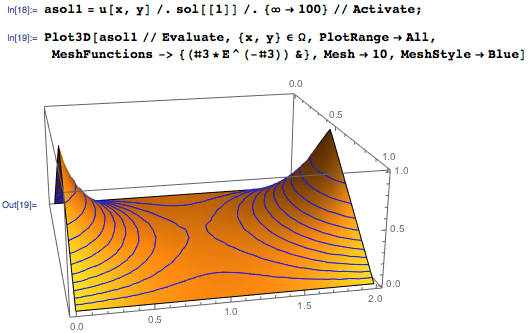
Как и в примерах ранее, мы можем извлечь некоторое количество членов (скажем, 100) из суммы и визуализировать решение:
Следует заметить, что решение u(x,y) задачи Дирихле представляется гладким в Ω, несмотря на то, что граничные условия имеют резкие черты. Помимо этого, u(x,y) достигает экстремальных значений на границах, в то время как в центре прямоугольника находится седловая точка. Эти черты характерны для линейных эллиптических уравнений — класса уравнений в частных производных, к которым и принадлежит уравнение Лапласа.
Волновое уравнение, уравнение теплопроводности, уравнение Лапласа — самые известные примеры классических УрЧП. Теперь мы рассмотрим три примера типичных современных УрЧП, первым среди которых будет уравнение Бюргерса для вязкой жидкости, которое может быть представлено следующим образом:
Это нелинейное УрЧП было введено Иоханнесом Бюргерсом в сороковых годах в качестве простой модели для турбулентных потоков (параметр ϵ в уравнении представляет собой вязкость жидкости). Однако, десять лет спустя, Э. Хопф и Д. Коул показали, что уравнение Бюргерса сводится к уравнению теплопроводности, а это значит, что данное уравнение не может проявлять хаотического поведения. Преобразование Коула-Хопфа позволяет решать уравнения Бюргерса в замкнутой форме для начального условия, заданного, к примеру, так:
В этом примере мы будем использовать функцию DSolveValue, которая возвращает только выражение для решения. Члены с функцией ошибок (Erf) в формуле ниже возникают из решения соответствующей граничной задачи теплового уравнения:
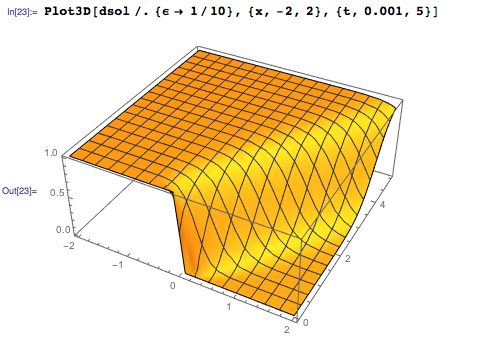
Представленный ниже график демонстрирует изменение во времени гипотетического одномерного поля скоростей потока. Решение представляется гладким для положительного ϵ, при том что начальное условие есть кусочно заданная функция:
Как можно заметить на нижепреведённых графиках, решение стремится к разрывному при сремлении вязкости ϵ к нулю. Подобные решения с резким переходом (shock solutions) — известная особенность уравнений Бюргерса для невязкой (ϵ = 0) среды.
В качестве второго примера современных УрЧП рассмотрим уравнение Блэка-Шоулза, используемое в финансовых расчётах. Это уравнение впервые представили Фишер Блэк и Майрон Шоулз в 1973 году в качестве модели для определения теоретической цены на европейские опционы, и формулируется оно следующим образом:
где:
c — цена опциона как функция от стоимости акций s и времени t,
r — процентная ставка без риска,
σ — волатильность акций.
В их эпохальной статье (которая была процитирована более 28000 раз), Блэк и Шоулз отметили, что их уравнения с помощью преобразования переменных могут быть сведены к уравнению теплопроводности. Это резкое упрощение приводит к знаменитой формуле Блэка-Шоулза для европейских опционов с конечными условиями, основанными на цене исполнения (strike price) k актива в момент времени t=Т:
Вооружившись этой формулой, мы можем вычислить значения финансовых опционов для типичных значений параметров:
Ответ согласуется со значением, полученным с помощью встроенной функции FinancialDerivative:
В качестве третьего примера современных УрЧП рассмотрим уравнение Шредингера для электрона в одномерной потенциальной яме с глубиной d и соответствующим начальным условием. Уравнение и условия можно сформулировать следующим образом:
Этот пример имеет элементарное решение, которое принимает мнимые значения из-за наличия I в уравнении Шредингера:
Функция плотности вероятности для электрона ρ = Ψ ⊹ Ψ, с использованием подходящих значений параметров в задаче, может быть вычислена следующим образом:
Мы можем создать анимацию изменения плотности вероятности во времени, которая показывает, что «центр» электрона в яме движется из стороны в сторону:
Собственные значения и собственные функции играют важную роль как в решении уравнения Шрёдингера, так и в других УрЧП. В частности, они предоставляют «строительные блоки» для решений волновых уравнений и уравнений теплопроводности в виде бесконечных сумм, которые приводились ранее в статье. Поэтому, в качестве нашего последнего примера рассмотрим задачу о нахождении девяти наименьших собственных значений и собственных функций для оператора Лапласа с однородным (нулевым) условием Дирихле для трехмерной сферической области. Найдем девять наименьших значений λ и соответствующих им функций ϕ, удовлетворяющих Λϕ = λ ϕ, которые определяются следующим образом:
Новая функция DEigensystem в версии 10.3 позволяет вычислить требуемые собственные значения и функции следующим образом:
Собственные значения в этой задаче выражаются через BesselJZero. Вот пример:
Собственные значения можно визуализировать с помощью функции DensityPlot3D, которая возвращает красивые графики, как показано ниже:
УрЧП являются важным инструментом во многих отраслях науки и техники, в статистике и финансах. На более фундаментальном уровне они предоставляют точные математические формулировки некоторых самых глубоких и тонких вопросов о нашей Вселенной, скажем, о возможности существования голых сингулярностей. По моему опыту, изучение УрЧП награждает редким сочетанием из практических идей и интеллектуального удовлетворения.
Рекомендую изучить документацию по DSolve, NDSolve, DEigensystem, NDEigensystem и методу конечных элементов, чтобы узнать больше о различных подходах к решению УрЧП в Wolfram Language.
УрЧП в символьной форме поддерживаются в Wolfram Mathematica и Wolfram Language с версии 10.3, а в ближайшее время будут представлены и во всех остальных программных продуктах Wolfram.
Видео:Уравнения в частных производных 1Скачать

Иллюстрированный самоучитель по Mathematica 3/4
Дифференциальные уравнения. Решение дифференциальных уравнений в символьном виде.
Дифференциальными принято называть уравнения, в состав которых входят производные функции у(х), представляющей решение уравнения. Дифференциальные уравнения могут быть представлены в различной форме, например в общеизвестной форме Коши:
Несколько дифференциальных уравнений образуют систему дифференциальных уравнений. Решение таких систем также возможно средствами Mathematica и подробно описано в ряде книг по использованию системы. Дифференциальные уравнения и системы дифференциальных уравнений могут быть линейными и нелинейными. Для линейных уравнений обычно существуют решения в аналитическом виде. Нелинейные дифференциальные уравнения в общем случае аналитических решений не имеют, но могут решаться приближенными численными методами.
Дифференциальные уравнения широко используются в практике математических вычислений. Они являются основой при решении задач моделирования – особенно в динамике. Немногие математические системы имеют реализации численных методов решения систем дифференциальных уравнений. Но система Mathematica имеет средства как для символьного, так и для численного решения дифференциальных уравнений и их систем.
Для решения дифференциальных уравнений в символьном виде используются следующие средства:
- DSolve[eqn, y[x], х] – решает дифференциальное уравнение относительно функций у [ х ] с независимой переменной х;
- DSolve[, , ] – решает систему дифференциальных уравнений.
У функции DSolve и ее численного варианта NDSolve есть пара опций, на которые следует обратить внимание:
- DSolveConstants – опция к DSolve, определяющая постоянные интегрирования, которые будут использованы в результате;
- StartingStepSize – опция к NDSolve, определяющая величину начального шага.
В решении дифференциальных уравнений встречаются постоянные интегрирования. По умолчанию они обозначаются как С [ i ].
Видео:Видео курс Wolfram Mathematica | Функции D и DtСкачать

Уравнения в частных производных wolfram mathematica
Достаточно войти на страницу wolframalpha набрать в текстовом поле свой запрос и нажать на кнопку «=»
(имеет всплывающую подсказку вычислить ) или просто нажать Enter .
Функционал Wolfram Alpha не ограничивается лишь поиском ответов на поставленные вопросы. С помощью этой системы можно, например, строить графики и сопоставлять различные данные, что намного наглядней и лучше воспринимается, чем просто текст. Кроме того, с помощью Wolfram Alpha можно производить математические операции, как элементарные (которые без проблем выполняет и Google), так и решать уравнения различной сложности. Также Wolfram Alpha умеет строить графики функций, вычислять значения синуса или косинуса и так далее.
Например можно решить вот такое уравнение :
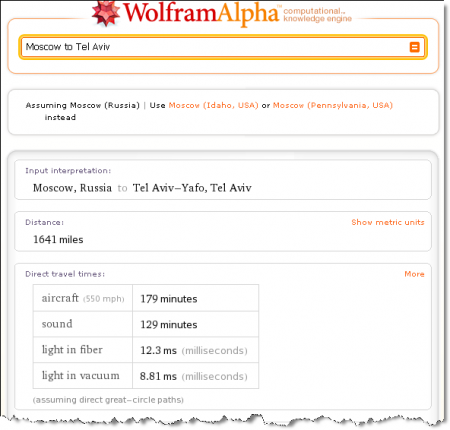
а чтобы узнать, какое расстояние между Москвой и Тель-Авивом, нужно ввести в поле
и вот вам результат:
Один из минусов сервиса Wolfram Alpha – это его англоязычность…так что если хотите задать вопрос системе придется писать его на английском языке. Даже неизвестно, появится ли русскоязычная версия этой поисково-вычислительной системы.
Основные команды для Вольфрам Альфа
(Команды вводятся в строку Вольфрама — например выше. Все команды заканчиваются нажатием Enter)
1. Решение уравнений, построение графиков
- Арифметические знаки плюс, минус, умножить, поделить +, — , *, / Примеры: 3*2, x*y, (a+b)/c
- Возведение в степень «x в степени а» x^a. Примеры x^a, x**a, (a+b)^2, (a+b)**2, (a+b)^(2x+1)
- Скобки. Действия в скобках ведутся первыми
- Функции .sin(x), cos(x), tan(x)=sin(x)/cos(x), cotan(x)=cos(x)/sin(x), sec(x)=1/cos(x), cosec(x)=1/sin(x)
- Функции log(x), exp(x), sinh(x), cosh(x), tanh(x), cotanh(x)
- Корень квадратный из «х» sqrt(x) или x^(1/2)
Чтобы вычислить выражение, нужно его просто ввести. Например корень из 2 будет выглядеть как sqrt(2) или же 2^(1/2).
2. Чтобы решить уравнение, нужно просто его ввести
3. Чтобы построить график, нужно использовать команду plot
Например нарисуем с помощью Вольфрама функцию 2^(-x) cos(x). Это делается командой plot (график).
Чтобы построить несколько графиков на одной координатной плоскости (например для визуализации решения систем уравнений), при значении переменной x в интервале (A,B), нужно использовать команду
4. Чтобы собрать множители из двучлена (многочлена) f, наберите factor[f]
5. Чтобы развалить произведение f на слагаемые, используйте команду expand[f]
6. Чтобы упростить выражение f[x], наберите команду Simplify[f[x]]
Например упростить «е в степени догарифм х»:
Simplify[ exp[ log[x] ] ]
Вольфрам альфа: интегралы
Как работать с Wolfram Alpha
Видео:Wolfram Mathematica, 1 занятие, осень 2020Скачать

Основные операции
- Сложение
: a+b
- Вычитание
: a-b
- Умножение
: a*b
- Деление
: a/b
- Возведение в степень
: a^b
Примеры
- 314+278; 314—278; 314*278; 314^278;
- (a^2+b^2)+(a^2-b^2); (a^2+b^2)/(a^2-b^2); (a+b)^(2+2/3).
Видео:КиЯ 0.18 | Решение уравнения и отображение его корней в Wolfram LanguageСкачать

Знаки сравнения
- Меньше
: : >
- Равно
: = или ==
- Меньше или равно
: =
Видео:Решение уравнений с помощь Solve WolframСкачать

Логические символы
- И
: &&
- ИЛИ
: ||
- НЕ
: !
Видео:Линейные дифференциальные уравнения в частных производныхСкачать

Основные константы
- Число
: Pi
- Число
: E
- Бесконечность
: Infinity, inf или oo
Видео:Wolframalpha : решение любых задач для студента по алгебре, вышке, физике, дифференциальные ур. и прСкачать

Основные функции
: x^a
: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
: sin[x] или Sin[x]
: tan[x] или Tan[x]
: cot[x] или Cot[x]
: sec[x] или Sec[x]
: csc[x] или Csc[x]
: ArcCos[x]
: ArcSin[x]
: ArcTan[x]
: ArcCot[x]
: ArcSec[x]
: ArcCsc[x]
: cosh[x] или Cosh[x]
: sinh[x] или Sinh[x]
: tanh[x] или Tanh[x]
: coth[x] или Coth[x]
: sech[x] или Sech[x]
: csch[x] или Csch[е]
: ArcCosh[x]
: ArcSinh[x]
: ArcTanh[x]
: ArcCoth[x]
: ArcSech[x]
: ArcCsch[x]
Видео:Wolfram Mathematica - 7. Решаване на СЛАУСкачать

Решение уравнений
Чтобы получить решение уравнения вида 
Примеры
- Solve[Cos[x]+Cos[2x]+Sin[4x]=0,x] или Cos[x]+Cos[2x]+Sin[4x]=0;
- Solve[x^5+x^4+x+1=0,x] или x^5+x^4+x+1=0;
- Solve[Log[3,x^2+x+1]-Log[9,x^2]=0,x] или Log[3,x^2+x+1]-Log[9,x^2]=0.
Если Ваше уравнение содержит несколько переменных, то запись: f[x, y,…,z]=0 даст весьма разнообразный набор сведений, таких как решение в целых числах, частные производные функции 
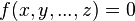

Примеры
- Cos[x+y]=0 или Solve[Cos[x+y]=0,x] или Solve[Cos[x+y]=0,y];
- x^2+y^2-5=0 или Solve[x^2+y^2-5=0,x] или Solve[x^2+y^2-5=0,y];
- x+y+z+t+p+q=9.
Видео:Wolfram Research Mathematica.Крамер.МатрицаСкачать

Решение неравенств
Решение в Wolfram Alpha неравенств типа 0″ src=»http://upload.wikimedia.org/math/3/d/9/3d97eb56e02c2889dd20a89529548180.png» />, 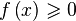

Примеры
- Cos[10x]-1/2>0 или Solve[Cos[10x]-1/2>0,x];
- x^2+5x+10>=0 или Solve[x^2+5x+10>=0,x].
Если Ваше неравенство содержит несколько переменных, то запись: f[x, y,…,z]>0 или f[x, y,…,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x, y,…,z]>0,j] или Solve[f[x, y,…,z]>=0,j], где 
Примеры
- Cos[x+y]>0 или Solve[Cos[x+y]>0,x] или Solve[Cos[x+y]>0,y];
- x^2+y^3-5 =9.
Видео:12.01 Решение систем ДУ в Wolfram MathematicaСкачать

Решение различных систем уравнений, неравенств и уравнений
Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом «И», который в Wolfram Alpha имеет вид &&.
Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида 


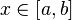


Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:Plot[f[x]&&g[x]&&h[x]&&…&&t[x],].
Для того, чтобы построить график функции 
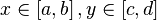


Видео:Уравнения в частных производных. Эллиптические уравнения.Скачать

Математический анализ
Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.
Пределы
Для того, чтобы найти предел последовательности 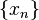
Примеры
- Limit[n^3/(n^4 + 2*n), n -> Infinity];
- Limit[(1+1/n)^n, n -> Infinity].
Найти предел функции 

Производные
Для того, чтобы найти производную функции 



Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Интегралы
Для того, чтобы найти неопределенный интеграл от функции 
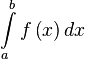
Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
Дифференциальные уравнения и их системы
Чтобы найти общее решение дифференциального уравнения 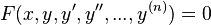
Если Вам требуется решить задачу Коши, то впишите: F[x, y, y’,y»,…], y[s]==A,y'[s]==B, …. Если нужно получить решение краевой задачи, что краевые условия, так же перечисляются через запятую, причем они должны иметь вид y[s]==S.
Решение систем дифференциальных уравнений также просто, достаточно вписать: , где f_1, f_2, …, f_n — дифференциальные уравнения, входящие в систему. К сожалению, решение задач Коши и краевых задач для систем дифференциальных уравнений пока-что не поддерживается.
Видео:Язык Wolfram Mathematica с нуля | #1 Первая программа на wolfram.Скачать

Ошибки при работе с системой
Система может допускать некоторые ошибки при решении сложных задач [1] . К примеру, если попытаться решить неравенство 
Видео:КиЯ 0.11 | Списки и их создание в Wolfram LanguageСкачать

Использование Wolfram Mathematica в решении дифференциальных уравнений
Саратовский национальный исследовательский государственный университет имени Н.Г. Чернышевского
NovaInfo55, с. 5-9
Опубликовано 20 ноября 2016
Раздел: Физико-математические науки
Просмотров за месяц: 49
CC BY-NC
Аннотация
В статье рассматриваются примеры решения обыкновенных дифференциальных уравнений в системе Wolfram Mathematica.
Ключевые слова
Текст научной работы
Системы компьютерной математики (Maple, Mathematica, MatLab, Derive и др.) применяются в различных областях науки. Они содержат процедуры для численных и аналитических расчетов, средства программирования, визуализации. В настоящее время пакеты прикладных программ используются не только при решении численных задач, но и при доказательстве теорем. Системы компьютерной математики используются в решении математических проблем в работах Д.С. Воронова, О.П. Гладуновой, Е.С. Корнева, М.В. Куркиной, Е.Д. Родионова, Я.В. Славолюбовой, В.В. Славского, Н.К. Смоленцева, Л.Н. Чибриковой и др.
Система компьютерной математики Wolfram Mathematica является одним из наиболее распространенных программных средств, которое позволяет выполнять численные, символьные вычисления, имеет развитую двумерную и трехмерную графику, а также встроенный язык программирования высокого уровня. Для знакомства с языком программирования Wolfram Language рекомендуется интернет-ресурс Wolfram Language & System «Documentation Center» (http://reference.wolfram.com/language/). Выбирая раздел, можно познакомиться с имеющимися командами для решения задач и с примерами их использования. Примеры использования Mathematica в решении геометрических задач приведены в 5.
Система Mathematica обладает обширными возможностями решения обыкновенных дифференциальных уравнений и их систем в символьном виде. Для этого используется функция DSolve, в алгоритме которой реализовано большинство известных на сегодняшний день аналитических методов.
Пример 1. Решим дифференциальное уравнение и построим график решений при различных значениях постоянной.
Пример 2. Решим уравнение y’=frac
Попытаемся решить уравнение с помощью функции DSolve:
В данном случае функция DSolve не может решить нелинейное уравнение. Поэтому запишем уравнение в виде:
и будем интегрировать обе части уравнения:
Следовательно, общее решение уравнения примет вид
-(-2+y^2)cos y+2ysin y=x-10ln (1-x)+13ln(2-x)+C
Пример 3. Решим дифференциальное уравнение и построим поле направлений и график решения уравнения при различных значениях константы.
Построим таблицу решений, заменив С[1] на a, где a изменяется от -2 до 2 с шагом 0,5:
Отобразим два графика одновременно и покажем, что векторы поля направлений являются касательными к решениям дифференциального уравнения:
Система Wolfram Mathematica используется для решения дифференциальных уравнений не только в математике, но и актуальна в других научных областях. Ее можно применять и в механике, в частности, для решения различных постановок задач, где в качестве математических объектов используются дифференциальные уравнения. В работах [6,7] рассмотрены уравнения движения мембран и акустических сред в виде обыкновенных дифференциальных уравнений. Для их решения может быть использована система компьютерной математики Wolfram Mathematica.
Читайте также
Математическая подготовка студентов в вузе в контексте будущей профессиональной деятельности
Использование прикладных программ при изучении математической статистики
Применение систем компьютерной математики при изучении комплексного анализа
Организация самостоятельной работы студентов в условиях информационно-образовательной среды вуза
Системы компьютерной математики в решении дифференциальных уравнений
Список литературы
- Букушева А.В. Использование Mathematica для описания геометрии динамических систем // Математика и ее приложения: фундаментальные проблемы науки и техники : сборник трудов всероссийской конференции, Барнаул, 24 — 26 ноября 2015. — Барнаул : Изд-во Алт. ун-та, 2015. С. 248-249.
- Букушева А.В. Применение Wolfram Language для выделения специальных классов почти контактных метрических структур // Компьютерные науки и информационные технологии : Материалы Междунар. науч. конф. — Саратов : Издат. центр.»Наука», 2016. С. 105-107.
- Букушева А.В. Использование систем компьютерной математики для решения геометрических задач сложного уровня // Информационные технологии в образовании: Материалы VI Всероссийской научно-практической конференции. – Саратов: ООО «Издательский центр «Наука»». 2014. – С. 76-77.
- Букушева А.В. Решение учебно-исследовательских задач с использованием систем компьютерной математики // Информационные технологии в образовании: Материалы VII Всеросс. научно-практ. конф. – Саратов: ООО «Издательский центр «Наука»», 2015. С.185-187.
- Букушева А.В. Учебно-исследовательские задачи в продуктивном обучении будущих бакалавров-математиков // Образовательные технологии. 2016. №2. С. 16-26.
- Вельмисова А.И. Распространение и отражение гармонических волн в плоском акустическом слое с гибкими стенками в случае разрыва упругих свойств на одной из стенок // Математика. Механика: Сб. науч. тр. Саратов: Изд-во Сарат. ун-та, 2010. Вып.12. С. 136-140.
- Вельмисова А.И., Вильде М.В., Кириллова И.В. Распространение и отражение гармонических волн в плоском акустическом слое с кусочно-неоднородными гибкими стенками // Известия Саратовского университета. Новая серия. Серия: Математика. Механика. Информатика. 2011. Т.11. №4. С. 68-73.
Цитировать
Зинина, А.И. Использование Wolfram Mathematica в решении дифференциальных уравнений / А.И. Зинина. — Текст : электронный // NovaInfo, 2016. — № 55. — С. 5-9. — URL: https://novainfo.ru/article/8754 (дата обращения: 23.02.2022).
Поделиться
Электронное периодическое издание зарегистрировано в Федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор), свидетельство о регистрации СМИ — ЭЛ № ФС77-41429 от 23.07.2010 г.
Соучредители СМИ: Долганов А.А., Майоров Е.В.

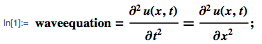
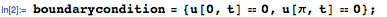
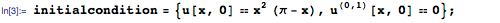
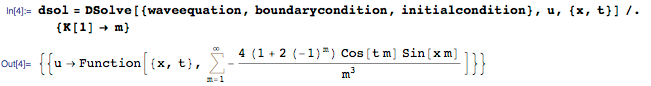
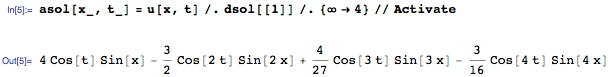
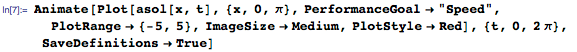
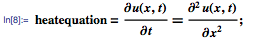
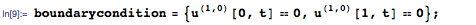
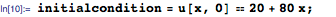

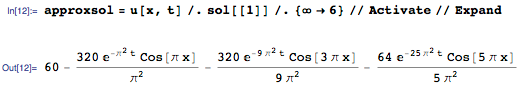
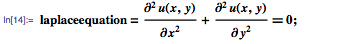
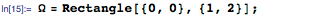


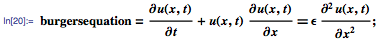
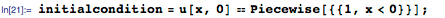


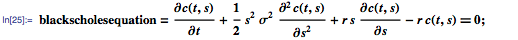

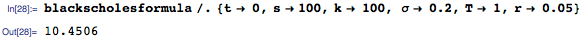

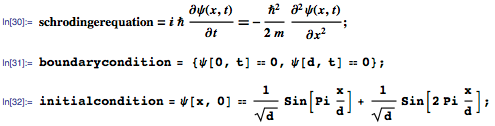



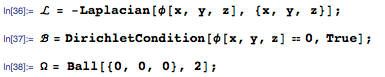
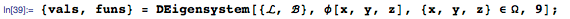
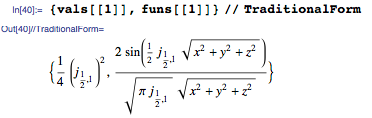


 : a+b
: a+b : a-b
: a-b : a*b
: a*b : a/b
: a/b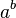 : a^b
: a^b : : >
: : > : = или ==
: = или == : =
: = : &&
: && : ||
: || : !
: ! : Pi
: Pi : E
: E : Infinity, inf или oo
: Infinity, inf или oo
 : x^a
: x^a : Sqrt[x]
: Sqrt[x] : x^(1/n)
: x^(1/n) : a^x
: a^x : Log[a, x]
: Log[a, x] : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x] : sin[x] или Sin[x]
: sin[x] или Sin[x] : tan[x] или Tan[x]
: tan[x] или Tan[x] : cot[x] или Cot[x]
: cot[x] или Cot[x] : sec[x] или Sec[x]
: sec[x] или Sec[x] : csc[x] или Csc[x]
: csc[x] или Csc[x] : ArcCos[x]
: ArcCos[x] : ArcSin[x]
: ArcSin[x] : ArcTan[x]
: ArcTan[x] : ArcCot[x]
: ArcCot[x] : ArcSec[x]
: ArcSec[x] : ArcCsc[x]
: ArcCsc[x] : cosh[x] или Cosh[x]
: cosh[x] или Cosh[x] : sinh[x] или Sinh[x]
: sinh[x] или Sinh[x] : tanh[x] или Tanh[x]
: tanh[x] или Tanh[x] : coth[x] или Coth[x]
: coth[x] или Coth[x] : sech[x] или Sech[x]
: sech[x] или Sech[x] : csch[x] или Csch[е]
: csch[x] или Csch[е] : ArcCosh[x]
: ArcCosh[x] : ArcSinh[x]
: ArcSinh[x] : ArcTanh[x]
: ArcTanh[x] : ArcCoth[x]
: ArcCoth[x] : ArcSech[x]
: ArcSech[x] : ArcCsch[x]
: ArcCsch[x]





