Установившимся режимом работы электрической сети при постоянных источниках тока и напряжения называется такое её состояние, при котором ток в любой ветви и напряжение в любом узле остаются относительно неизменны-ми в течение сколь угодно длительного времени.
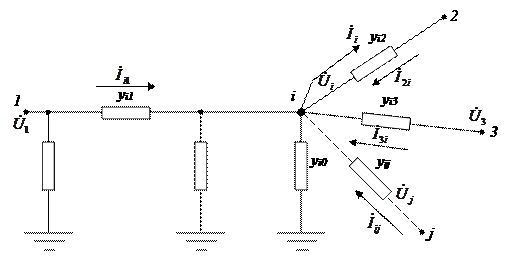
Рассмотрим узел электрической сети, в котором соединены несколько ветвей. В качестве ветвей могут быть участки ЛЭП, трансформаторы, батареи статических конденсаторов (БСК), синхронные компенсаторы (СК) и другие элементы электрической сети.
1,2,3,…,j – номера узлов, имеющих электрическую связь с рассматриваемым
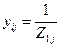
yi0 – проводимость i — го узла, включающая проводимости (поперечные)
элементов, установленных в i – м узле (БСК, СК, реакторы, и другие
элементы), половины поперечных проводимостей линий, подключен-
ных в i – м узле, поперечные проводимости трансформаторов (если
они примыкают к этому узлу узлом начала схемы замещения).
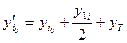
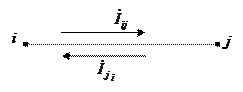

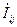
Расчетное направление тока или мощности может не совпадать с реальным.
В этом случае они будут отличаться знаками.
В соответствии с I — законом Кирхгофа в узле i должен соблюдаться баланс токов, то есть сумма токов в ветвях, присоединенных к узлу (с учетом направ-лений токов ) должна быть равна инъекции тока в узле:
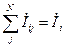
N – количество узлов непосредственно связанных с i – м узлом.
Инъекцию тока в узле Іi можно определить:
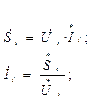
Левая часть уравнения выражения (1):

Объединим выражения (2) и (3), и запишем формулу (1):
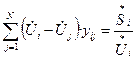
Умножим обе части уравнения (4) на 

Рассмотрим левую часть уравнения (4). Запишем баланс токов в i – м узле в развернутом виде:
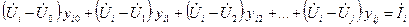
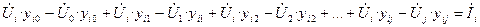
Сгруппируем элементы в левой части:
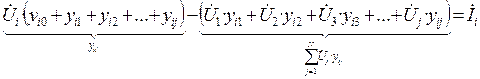
yij – взаимная проводимость узлов i и j. Равна продольной проводимости участка i – j : yij = 1 / Zij .
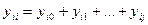
Во вторых скобках – сумма произведений напряжений узлов, соединенных с i – м, на их взаимные проводимости.
Запишем уравнение (8) с учетом принятых обозначений:
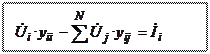
(9) Оно описывает режим i — го узла и
баланс токов в нём.
Неизвестным являются напряжения узлов: 
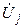
Заданные величины: инъекция тока 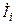
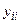
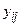
Подставим в правую часть формулы (9) формулу (2):
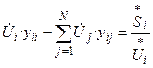
Умножим обе части уравнения (10) на 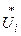
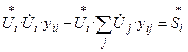
Получаем уравнение установившегося режима в форме баланса мощности:
Описывает баланс мощностей в i – м узле.
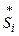
Неизвестные величины: напряжения в узлах 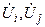
Известные величины: 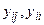
Уравнение (11) — нелинейное относительно неизвестных напряжений.
1. Уравнения (9) и (11) – уравнения с комплексными неизвестными и
комплексными неизвестными. Содержат параметры, характеризую-
щие схему сети (проводимости yii и yij) и её режим ( напряжения Ui
2. Неизвестными величинами в них являются напряжения узлов Ui и Uj ;
3. Известные величины в них – собственная и взаимные проводимости
узлов. Заданные величины – ток и мощность в узле;
4. Уравнения записаны для одного узла электрической сети. Для схемы,
состоящей из N узлов, потребуется записать систему из N таких
Лекция 8
В практических расчетах комплексные уравнения (9) и (11) часто исполь-зуются в преобразованном виде. Комплексные величины в их составе пред-ставляются в виде действительных и мнимых составляющих. В результате, комплексное уравнение распадается на два действительных уравнения.
Преобразуем уравнение (11), представив неизвестные напряжения (комп-лексные величины) Ui ,Uj в прямоугольных координатах:
Проводимости тоже представим в виде составляющих:
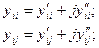
Мощность: 
Подставим эти значения в (11):
Выполняем преобразование: раскрываем скобки, группируем, разделяем действительную и мнимую части уравнения. Получаем два действительных
уравнения установившегося режима в форме баланса мощностей, записанных в прямоугольных координатах:

Неизвестные величины в них — составляющие напряжений Ui ’ , Ui ” , Uj ’ , Uj ” .
Уравнение (13) описывает баланс активной и реактивной мощности в одном i – м узле сети. Для сети, состоящей из n узлов нужно записать 2n таких урав-нений. Неизвестными являются составляющие напряжения 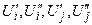
Представим уравнение (11) в полярных координатах. Для этого комплексы неизвестных напряжений запишем в соответствии с формулой Эйлера:
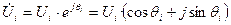
Здесь Ui – модуль, 
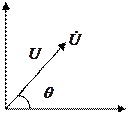 |
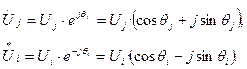
Подставим (14) в (11) учетом того, что
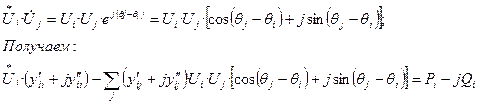
Преобразуем уравнение (15): раскрываем скобки, группируем, разделя-ем действительные и мнимые части, меняем местами
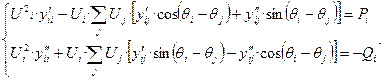
Это уравнение установившегося режима в форме баланса мощности,
записанное в полярных координатах. Неизвестные величины в нём — модули напряжений 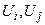
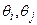
Это два действительных уравнения, записанные для одного i-го узла схемы. Определяют баланс активной и реактивной мощности в нем.
Существуют и другие формы записи уравнений установившегося режима.
Пример:
Составить уравнения в форме баланса токов для каждого из узлов сети
Составим уравнение для первого узла.
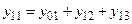
Для узла 0: i=0; j=1; n=1;
Для узла 2: i=2; j=1,3; n=2;
Для узла 3: i=3; j=1,2; n=2;
Уравнения в форме баланса мощностей можно получить, если умножить каждое из полученных уравнений на сопряженный комплекс соответствующе-го напряжения.
Запишем уравнение для 1 – го узла в прямоугольных координатах:
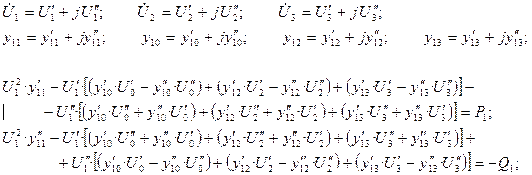
Для узлов 2 и 3 уравнения в прямоугольных координатах записать самостоятельно.
Уравнения для 1-го узла в полярных координатах:
- Установившийся режим
- Содержание
- Общие положения
- Расчёт параметров установившегося режима
- Представление элементов энергосистемы
- Генератор
- Трансформатор
- Нагрузка
- Линии электропередачи
- Выключатели
- Шунтовые элементы
- Связь с соседней энергосистемой
- Курсовая работа: Расчет установившегося режима работы электрической системы
- Реферат
- Содержание
- Введение
- 1. Описание
- Таблица 1
- 2. Определение параметров схемы замещения электрической системы. Формирование матрицы узловых проводимостей
- 2.1 Схемы замещения элементов электрической системы
- 2.1.1 Схема замещения ВЛ-500 кВ и определение ее параметров
- 2.1.2 Схема замещения автотрансформатора АОДЦТН-167000/500/220
- 2.1.3 Схема замещения ВЛ-220 кВ, определение ее параметров
- 2.1.4 Схема замещения автотрансформатора АТДЦТН-200000/220/110
- 2.1.5 Схема замещения трансформатора ТРДЦН-100000/220
- 2.2 Схема замещения электрической системы
- 2.3 Расчетная схема
- 2.4 Диагональная матрица проводимостей ветвей
- 2.5 Граф расчетной схемы
- 2.6 Расчет матрицы узловых проводимостей
- 3. Нелинейные уравнения установившегося режима
- 3.1 Метод Зейделя
- 3.2 Метод Ньютона
- Заключение
- Список использованной литературы
Видео:Цель расчета режимовСкачать

Установившийся режим
Установившийся режим — это режим работы энергосистемы, при котором параметры режима могут приниматься неизменными [1] .
Видео:Метод узловых потенциалов. Самое простое и понятное объяснение этого методаСкачать

Содержание
Видео:Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Общие положения
Состояние энергосистемы можно считать установившимся (стационарным), если параметры описывающие её поведение, не меняются с теченеием времени или меняются по периодическому закону от времени (с постоянным периодом, амплитудой и фазой). При этом математическую модель исследуемых процессов в энергсосистеме можно упростить до системы линейных (нелинейных) уравнеий, вместо рассмотрения системы диффференциальных (интегро-дифференциальных) уравнений.
Очевидно, что в достаточно крупной энергосистеме полностью установившегося режима не существует, так как с увеличением числа элементов объединённых в энергосистему, вероятность того, что хотя бы один из изменит своё включённое состояние или свой режим работы достаточно велика. Вследствие этого, можно считать, что в единой энергосистеме постоянно происходит один или несколько переходных процессов и энергосистема постоянно находится в переходном режиме. С другой стороны, для исследования большинства процессов в крупной энергосистеме можно рассматривать квазиустановившиеся режимы, то есть такие режимы когда параметры изменяются незначительно и данным изменениями можно пренебречь.
Исследование параметров установившегося режима энергосистемы важно для решения целого ряда практических задач которые перечислены здесь.
При расчётах установившихся режимов необходимо иметь ввиду, что они должны отвечать определённым требованиям общефизического характера. Из этих соображений в первую очередь вытекает требование возможности существования установившегося режима, при этом необходимым условием существования является устойчивость этого режима. Достаточным условием для существования установившегося режима является возможность его технической осуществимости.
Любой установившийся режим, который возникает после окончания переходного режима, требует для своего существования сбалансированности мощности нагрузки и генерации (с учётом потерь на передачу), то есть в энергосистеме должен установиться некоторый баланс мощности и энергии.
Видео:Принцип работы трансформатораСкачать

Расчёт параметров установившегося режима
Электрическая сеть высокого напряжения (более 35 кВ) для передачи и распределения электроэнергии относится к категории электрических цепей, поэтому к расчёту её режима следовало бы применить общие методы теории электрических цепей.
На практике применение этих методов встречает ряд трудностей, вызванных как наличием большого количества элементов, образующих электрическую сеть, так и специфическими особенностями задания исходных данных.
Пусть задана мощность некоторого нагрузочного узла [math]dot_i = P_i + j cdot Q_i [/math] , которая должна быть учтена, наряду с другими нагрузками, при расчёте УР сети. Ток [math]i[/math] -го нагрузочного узла равен:
[math] displaystyledot_i =frac<widehat_i> <sqrtwidehat_i> [/math]
и, следовательно, может быть вычислен только при известном напряжении [math]dot_i[/math] на шинах этой нагрузки. Однако именно напряжения в узлах электрической сети является искомой величиной. Это обстоятельство препятствует непосредственному использованию законов Киргофа для получения однозначного решения, в связи с чем практическое применение нашли другие методы решения, в том числе методы последовательных приблежений (итерационные метод). Данные методы основаны на последовательном уточнении напряжения в узлах электрической сети, причём в качестве начального приближения напряжений может быть использоавно разумное допущение о том, что напяржения во всех узлах в нормальном режиме не могут существенно отличаться от номинального напряжения данного класса сети. Введение такого допущения позволяет определить приближённо (на каждой итераци) потери пощности в каждом сетевом элементе и нагрузочные токи. Но знаение значение величины тока по концам сетевых элементов непосредственно связано с значением напряжения в узлах примыкания, которые считаются неизвестными, является достаточным для того, чтобы определить новое приближение напряжения. В результате итерацинного уточнения параметров УР становятся известными напряжения во всех узлах электрической сети.
При расчёте параметров установившегося режима обычно принимают следующие основные допущения:
- Частота в энергосистеме неизменна.
- Высшие гармонические составляющие отсутствуют.
- Взаимоиндукция между элементами не учитывается (в случае использования однолинейных расчётных схем).
- Нагрузка по фазам симметрична (в случае использования однолинейных расчётных схем).
- Параметры установившегося режима не зависят от времени.
- В большинстве случаев влияние внешних факторов (интенсивность освещения, скорость ветра, наличие глолёда, изменение электрчиеские параметров при механических деформациях и т. д.) не учитывается.
- Линии электропередачи представлены сосредоточенными параметрами (при длинах линий менее 5 % от длины электромагнитной волны).
Расчёт установившегося режима заключается в оценке всех параметров режима (в первую очередь узловых напряжений и потоков мощностей по ветвям), при заданных параметрах электрической сети:
- схема соединений элементов электрической сети;
- электрические параметры элементов (сопротивления, проводимости шунтов, коэффициенты трансформации и т. д.);
- мощности нагрузок, а также их статические характеристики по напряжению;
- мощности генераторов и диапазон регулирования реактивной мощности.
Математическое моделирование установившегося режима требует составление математического описания электрической сети. Это описание в первую очередь базируется на расчётной схеме, которая представляет собой идеализацию реальной электрической сети.
Под математической моделью электрической сети можно понимать систему уравнений связывающих параметры схемы замещения (исходной информации по элементам расчётной схемы) и неизвестных параметров установившегося режима. Важно отметить, что для одной и той же схемы замещения можно составить различные системы уравнений (математические модели), обладающие разными вычислительными характеристиками. Основные математические модели для оценки параметров установившегося режима:
Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Представление элементов энергосистемы
Видео:Электромеханические переходные процессы. Устойчивость. Уравнение движение ротора.Скачать
Генератор
В установившемся режиме генераторы обычно представляют двумя способами:
- Источник постоянного напряжения и активной мощности (PV узел).
- Источник постоянной активной и реактивной мощности (PQ узел).
В случае когда генератор представлен источником постоянного напряжения, необходимо в процессе расчётов, учитывать регулировочный диапазон по реактивной мощности. Зачастую эта задача решается алгоритмически в ходе итерационной оценки параметров установившегося режима. В случае, если оценка величины реактивной мощности превышает регулировочный диапазон, то генератор необходимо представить в виде PQ узла.
Видео:42) АНАЛИЗ САУ В УСТАНОВИВШЕМСЯ РЕЖИМЕ. Часть I. Статическое и астатическое регулированиеСкачать

Трансформатор
Трансформатор в расчётах обычно представлен в виде ветвей с сосредоточенными параметрами и постоянным коэффициентом трансформации. Более подробно представление трансформатора в установившихся режимах рассмотрено здесь.
Видео:Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

Нагрузка
Нагрузочные узлы обычно представлены в виде узлов с известной активной и реактивной мощности и в математической модели обычно представлены следующим образом:
- Зависимость активной и реактивной мощности заданы некоторой функциональной зависимостью от напряжения, называемой статической характеристикой нагрузки.
- Постоянное значение потребления активной и реактивной мощности. С формальной точки зрения это тоже статическая характеристика нагрузки, при которой мощность не зависит от напряжения.
Видео:Бакалавриат_ЭЭ_7 семестр_ПЭП_Математические методы расчета установившихся режимов СЭС_Лекция 3Скачать

Линии электропередачи
В электрической сети для передачи электрической энергии служат кабельные и воздушные линии электропередач. В реальности сопротивление линии электропередачи распределено по всей её длине, что приводит к необходимости учитывать её волновые свойства, но это в значительной степени усложняет методы оценки параметров установившегося режима по математической модели. По этой причине линии электропередачи обыно представлены в виде сосредоточенных сопротивлений и шунтов (или цепочки сосредоточенных сопротивлений и шунтов). Более подробно схема замещения линии электропередачи рассмотрена здесь.
Видео:Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Выключатели
При подробном моделировании схемы распределительного устройства подстанции возникает необходимость представления выключателей в расчётной математической модели.
В практике расчётов наибольше распространение получили математические модели на основе уравнений узловых напряжений. Основной трудностью моделирования выключателей в таких моделях является их низкое электрическое сопротивление [math]Z lt lt 1 [/math] [Ом]. Этот факт приводит к следующим трудностям при составлении математической модели:
- Пусть [math]Z = 0 [/math] [Ом], при составлении уравнений узловых напряжений в матрице проводимостей появляются элементы с бесконечными проводимостями, что делает невозможным поиск решения этой системы.
- Для решения первой проблемы выключатель можно представить в виде очень маленького сопротивления [math]R = 0,001 [/math] [Ом], что может привести к расчётной неустойчивости в случае когда к узлу примыкают только выключатели.
- В случае исключения выключателей выключателей из расчётной модели потребуется дополнительные алгоритмы для оценки потоков активной и реактивной мощности через выключатель.
Видео:ПРОСТЫМ ЯЗЫКОМ: Что такое трансформатор?Скачать

Шунтовые элементы
Для регулирования напряжения в узлах электрической сети применяются различные управляемые и неуправляемые компенсирующие устройства. С точки зрения математической модели все эти устройства можно представить в виде шунтов в узлах. Более подробно схемы замещения компенсирующих устройств рассмотрены здесь.
Видео:АТТП - Коммутирующие устройства. Логические уравнения. Самостоятельная работа в TIA PortalСкачать

Связь с соседней энергосистемой
Для моделирования места подключения к соседней энергосистеме обычно используют концепцию шин бесконечной мощности. В этом узле должен быть задан фиксированный модуль и угол напряжения (узел [math]Vdelta[/math] . Расчётными величинами будут значения активной и реактивной мощности.
Важно отметить, что выбор величины модуля напряжения и угла может значительно повлиять на оценку параметров установившегося режима.
Видео:Моделирование СМ Часть 4 Установившийся режим синхронной машиныСкачать

Курсовая работа: Расчет установившегося режима работы электрической системы
| Название: Расчет установившегося режима работы электрической системы Раздел: Рефераты по физике Тип: курсовая работа Добавлен 04:40:50 20 ноября 2009 Похожие работы Просмотров: 1367 Комментариев: 18 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | l2 |  |  | |||||
 |  |  |  |  |  |  |  |  |  |
| 220 | АС400/51 | 110 | АС300/39 | 200 | АС400/51 | 110 | АС500/64 | 220 | АС240/32 |
Данные по нагрузкам приведены в табл. 2.
 |  |  |  |  |
 |  |  |  |  |
Видео:Электромеханические переходные процессы. Динамическая устойчивость. Метод площадей.Скачать

2. Определение параметров схемы замещения электрической системы. Формирование матрицы узловых проводимостей
Определим параметры схемы замещения элементов электрической системы. Все удельные параметры для ВЛ и каталожные данные трансформаторов находим по справочным данным.
Все параметры схем замещения приводим к номинальному напряжению 220 кВ.
2.1 Схемы замещения элементов электрической системы
2.1.1 Схема замещения ВЛ-500 кВ и определение ее параметров
Двухцепная ВЛ-500 кВ выполнена с расщеплением фазы на три провода марки АС-400/51. Длина линии
Схема замещения ВЛ-500 кВ изображена на рис. 2.
На 100 км длины 


Приведение параметров к номинальному напряжению происходит путем умножения их на коэффициент трансформации в квадрате (

2.1.2 Схема замещения автотрансформатора АОДЦТН-167000/500/220
Схема замещения трансформатора представлена на рис. 3.
Каталожные данные автотрансформатора АОДЦТН-167000/500/220:
Параметры поперечной ветви:
Рассчитаем 
рассчитаем активные сопротивления каждой фазы:
рассчитаем 
рассчитаем реактивные сопротивления каждой фазы:
рассчитаем приведенные активные сопротивления каждой фазы:
рассчитаем приведенные реактивные сопротивления каждой фазы:
Рассчитаем полные сопротивления каждой фазы и полную проводимость поперечной ветви:
2.1.3 Схема замещения ВЛ-220 кВ, определение ее параметров
Для ВЛ-220 кВ допустимо не учитывать потер на корону. Схема замещения ВЛ-220 кВ изображена на рис. 4.
Двухцепная линия 
Длина линии 
На 100 км: 


Одноцепная линия 
Длина линии 
На 100 км: 


Одноцепная линия 
Длина линии 
На 100 км: 


Одноцепная линия 
Длина линии 
На 100 км: 


2.1.4 Схема замещения автотрансформатора АТДЦТН-200000/220/110
Схема замещения автотрансформатора аналогична схеме замещения автотрансформатора АОДЦТН-167000/500/220
Каталожные данные автотрансформатора АТДЦТН-200000/220/110:
Параметры поперечной ветви:
Рассчитаем 
рассчитаем активные сопротивления каждой фазы:
рассчитаем 
рассчитаем реактивные сопротивления каждой фазы:
рассчитаем приведенные активные сопротивления каждой фазы:
рассчитаем приведенные реактивные сопротивления каждой фазы:
Рассчитаем полные сопротивления каждой фазы и полную проводимость поперечной ветви:
2.1.5 Схема замещения трансформатора ТРДЦН-100000/220
Схема замещения двухобмоточного трансформатора изображена на рис. 5.
Каталожные данные трансформатора ТРДЦН-100000/220:
Параметры схемы замещения:
2.2 Схема замещения электрической системы
На рис. 8 изображена схема замещения электрической системы. Все параметры схемы замещения рассчитаны в пункте 2.1.
2.3 Расчетная схема
Просуммировав проводимости, имеющие общий узел, и объединив все нейтрали N в один узел, получим расчетную схему.
Расчетная схема с пронумерованными ветвями и буквенными обозначениями узлов изображена на рис. 9.
2.4 Диагональная матрица проводимостей ветвей 
Т.к. количество ветвей следуемой расчетной схемы – 17, то размерность матрицы проводимостей ветвей – 17´17. Определим диагональные элементы матрицы 
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| 1 | Y0 /2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | Yz0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | Y6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | Yatvn | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | Yatnn | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | Yatsn | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | Y7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Yz1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Yzt1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Y8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Yz2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Yzt2 | 0 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Y9 | 0 | 0 | 0 | 0 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Yz5 | 0 | 0 | 0 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Yz3 | 0 | 0 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Yzt3 | 0 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Y10 |
2.5 Граф расчетной схемы
По расчетной схеме, изображенной на рис. 9. составим граф. Для каждой ветви графа расчетной схемы произвольно задается направление. Граф расчетной схемы изображен на рис. 10.
По графу составляем матрицу соединений ветвей узлов (первая матрица инциденций) — 
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| A | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| B | 0 | -1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| D | 0 | 0 | 0 | -1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| E | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| F | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| G | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 |
| I | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 1 | -1 | 0 | 0 | 0 |
| J | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | -1 | 1 | 1 |
| K | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 |
| O | -1 | 0 | -1 | 0 | 0 | 0 | -1 | 0 | 0 | -1 | 0 | 0 | -1 | 0 | 0 | 0 | -1 |
В матрице 
Запишем матрицу M :
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| A | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| B | 0 | -1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| D | 0 | 0 | 0 | -1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| E | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| F | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| G | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 |
| I | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 1 | -1 | 0 | 0 | 0 |
| J | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | -1 | 1 | 1 |
| K | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 |
2.6 Расчет матрицы узловых проводимостей 
Матрица узловых проводимостей 
где 


Решая матричное уравнение
в среде MathCAD, получена следующая матрица узловых проводимостей 
Видео:Расчёт потерь мощности на участке электрической сетиСкачать

3. Нелинейные уравнения установившегося режима
Нелинейные уравнения узловых напряжений описывают установившийся режим электрической системы при задании нелинейных источников тока. В схеме замещения электрической системы нелинейным источникам тока соответствуют генераторы с заданной мощностью, либо нагрузки потребителей, заданные статической характеристикой или постоянной мощностью. При заданной мощности нагрузки потребителя и генератора ток задается в следующем виде:
где 




В матричной форме уравнения узловых напряжений имеют вид:
где 



Записанное уравнение – уравнение узловых напряжений в форме баланса токов.
Уравнения узловых напряжений можно записать в форме баланса мощности. В матричной форме:
где 


Нелинейные уравнения установившегося режима в общей форме можно записать в виде системы неявных функций:
где 


При расчетах вектор независимых переменных задан, т.е. 
Нелинейную систему можно записать:
3.1 Метод Зейделя
Метод Зейделя может применяться для решения нелинейных уравнений узловых напряжений в форме баланса токов. Итерационный процесс Зейделя определяется выражением:
Сходимость метода Зейделя к решению нелинейных уравнений установившихся режимов медленная. Для ускорения сходимости метода Зейделя применяются ускоряющие коэффициенты. Основное достоинство метода Зейделя состоит в том, что он легко программируется и требует малой оперативной памяти. Недостаток метода – в медленной сходимости, или расходимости. Метод Зейделя особенно медленно сходится и расходится в расчетах установившихся режимов электрических систем с устройствами продольной компенсации, с трехобмоточными трансформаторами или автотрансформаторами с очень малым сопротивлениями обмотки среднего напряжения и для систем с сильной неоднородностью параметров.
Результаты решения нелинейных уравнений узловых напряжений в форме баланса токов в среде MathCAD методом Зейделя, а так же сама программа расчета, приведены в Приложении.
3.2 Метод Ньютона
Идея метода Ньютона состоит в последовательной замене на каждой итерации системе нелинейных уравнений некоторой линейной системой, решение которой дает значение неизвестных, более близкие к решению нелинейной системы, чем исходное приближение.
Рассмотрим решение по методу Ньютона системы нелинейных уравнений с действительными переменными:
Если использовать вектор-столбец 


то систему нелинейных уравнений можно записать в матричном виде:
Пусть 


Запишем матрицу Якоби, т.е. матрицу производных системы функций 

Тогда систему линеаризованных уравнений можно зависать в матричном виде:
Эта система линейна относительно поправок

Матрица Якоби не должна быть вырожденной, тогда решая полученную систему (линейную) любым способом, находим первое приближение переменных:
Каждый шаг итерационного процесса состоит из решения линейной системы:
и определения следующего приближения неизвестных:
Контроль сходимости осуществляется по вектору невязок:
Уравнение узловых напряжений в форме баланса мощностей для 
Слагаемое 

Выделим в уравнении действительные и мнимые части:
где 




В расчетах на ЭВМ обычно в качестве неизвестных используются модули и фазы напряжений узлов 

Уравнение баланса мощностей для 


где
Уравнение в форме баланса мощностей:
С учетом реальных условий в электрических системах можно пренебречь недиагональным элементами матрицы Якоби, т.е.
Метод Ньютона очень быстро сходится и имеет высокую надежность.
Результаты решения нелинейных уравнений узловых напряжений в форме баланса мощностей в полярной системе координат в среде MathCAD методом Ньютона, а так же сама программа расчета, приведены в Приложении.
Заключение
В курсовой работе была рассмотрена сложная электрическая система. Подробно рассмотрено составление схемы замещения электрической системы и расчет матрицы узловых проводимостей. Приводятся основные методы решения нелинейных уравнений установившегося режима работы электрической системы. Разработана программа в среде MathCAD для решения нелинейных систем методам Ньютона и Зейделя. Предпочтение отдается методу Ньютона из-за высокой надежности и быстрой сходимости.
Список использованной литературы
1. «Справочник по проектированию электроснабжения, линий электропередачи и сетей». Под ред. Я.М. Большама, В.И. Круповича, М.Л. Самовера; М.: «Энергия», 1974г.
2. «Справочник по электроснабжению промышленных предприятий». Под ред. А.А. Федорова, Г.В. Сербиновского. М.: «Энергия», 1973г.
3. «Электрические системы и сети». Под ред. Л.Н. Баптиданова. Л.: «Госэнергоиздат», 1963г.
4. Конспекты лекций по «Математическим задачам в энергетике».


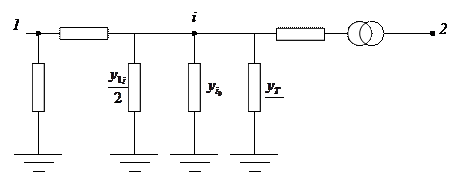
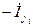

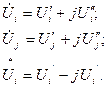


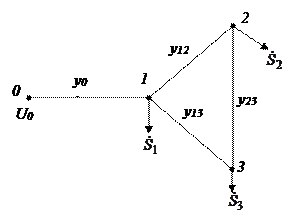


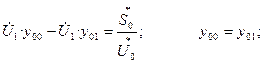
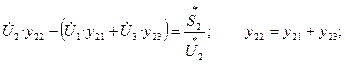
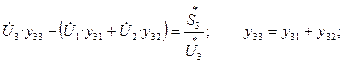


![[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]](https://i.ytimg.com/vi/agDRxLaUWI4/0.jpg)





































































