Уравнения трех моментов в примерах

Как мы выяснили ранее, метод сил (метод перемещений) хорошо применим для двух- трехпролетных неразрезных балок. При больших степенях статической неопределимости вычисления методом перемещений становятся слишком громоздкими. Частично решить эту проблему помогает метод, основанный на рассмотрении углов поворота поперечных сечений балки на опорах. Этот метод условно можно назвать методом моментов.

Частично потому, что количество дополнительных уравнений, необходимых для определения значений опорных реакций, остается таким же, а вот количество неизвестных в таких уравнениях уменьшается до трех. По большей части теоретические предпосылки этого метода такие же как и у метода сил, и ограничения по жесткости и неподатливости опор в вертикальном направлении остаются те же, вот только изменяется подход к рассмотрению балки.

В данном случае многопролетная, статически неопределимая балка как бы рассекается на промежуточных опорах на множество однопролетных, статически определимых балок.

Для начала рассмотрим пример с двухпролетной балкой, какую мы рассматривали при описании метода сил.

1. Двухпролетная балка

Рисунок 315.1. Приведение двухпролетной балки к основной и вспомогательной системам при методе моментов.

1. Когда мы рассекаем балку на промежуточной статически неопределимой опоре (рис. 315.1.б)), мы получаем две статически определимых балки с общей опорой В (рис.315.1.в)). Рассчитать такие балки — не проблема, а для удобства расчетов даже созданы соответствующие таблицы, пример такой таблицы можно посмотреть здесь. Балки, показанные на рисунке 315.1.в), являются элементами основной системы. Балки, показанные на рисунке 315.1.г), являются элементами вспомогательной системы.

2. Под действием приложенной нагрузки поперечные сечения балок не будут находиться в плоскости, перпендикулярной к основной оси (оси х), а будут иметь некоторый наклон. Другими словами, между плоскостью, перпендикулярной к основной оси, и поперечным сечением будет некоторый угол, называемый углом поворота поперечного сечения Θ. На рисунке 315.1.е) показаны углы поворота для крайнего правого сечения левой балки и крайнего левого сечения правой балки. Таким образом между указанными поперечными сечениями образуется угол наклона φ. Общая эпюра углов поворотов поперечных сечений для статически определимых балок основной системы будет выглядеть приблизительно так, как показано на рисунке 315.1.д).

3. Между тем балка-то у нас неразрезная, а это означает, что угол между двумя очень близкими относительно оси х сечениями будет стремиться к нулю, а так как мы рассекаем балку мысленно, то крайнее правое сечение левой балки и крайнее левое сечение правой балки — это одно и то же поперечное сечение неразрезной балки и для такого сечения угол наклона φ = 0.

4. Если к рассматриваемым поперечным сечениям балок приложить изгибающие моменты (рис. 315.1.г), то при определенном значении моментов суммарный угол наклона поперечных сечений будет равен углу наклона между поперечными сечениями балок основной системы, только значение это будет иметь обратный знак (рис.315.1.ж).

5. Таким образом, если сложить угол наклона смежных поперечных сечений балок основной системы и угол наклона смежных поперечных сечений балок вспомогательной системы, то угол наклона φ на общей эпюре углов поворотов будет равен нулю (рис.315.1.и)), при этом угол поворота поперечного сечения Θ неразрезной балки может быть не равен нулю.

6. Так как в действительности никакие внешние моменты на статически неопределимых опорах не прикладываются, а мы всего лишь заменяем внутренние напряжения внешними моментами, то на суммарной эпюре моментов (на рисунке 315 не показана) на статически неопределимых опорах не может быть скачков (могут быть только точки экстремума). Из этого следует, что значение момента, приложенного к крайнему правому сечению, должно быть равно значению момента, приложенного к крайнему левому сечению:

М л = М п = М (315.1.1)

Примечание: Самое трудное при работе с моментами и углами поворота — уследить за знаками. Сейчас считается, что если сила или момент приводят к растяжению нижней части сечения, то эпюра моментов рисуется снизу, но такой момент считается положительным, соответственно, если сила или момент приводят к растяжению верхней области сечения, то эпюра моментов рисуется сверху, но такой момент считается отрицательным. Дело в том, что вне зависимости от того, сверху или снизу рисуется эпюра моментов в поперечных сечениях рассматриваемых конструкций возникают нормальные напряжения и если рассматривать только нижнюю часть сечения, то положительный момент означает растяжение в нижней части и таким образом знак «+» символизирует увеличение длины в нижней части рассматриваемой конструкции, а отрицательный момент означает сжатие в нижней части сечения и знак»-» символизирует уменьшение длины конструкции в нижней части. Из этого следует, что если момент для рассматриваемого сечения (точки на оси х) направлен по часовой стрелке, то такой момент положительный, а если против часовой стрелки, то момент отрицательный. Таким образом знак момента зависит от точки (поперечного сечения), относительно которой данный момент рассматривается. Так для смежных статически определимых балок моменты, показанные на рисунке 315.1.г), будут отрицательными, а для поперечного сечения на опоре В неразрезной балки моменты будут иметь различный знак и в сумме дадут ноль. Приблизительно то же самое можно сказать и о углах поворота поперечных сечений. Если сечение наклонено вправо от оси у, то такой угол поворота можно считать отрицательным, если влево от оси у, то такой угол поворота будет считаться положительным, что и отражено на соответствующих эпюрах углов поворотов на рисунке 315.1. Между тем при определении прогиба знак угла поворота крайних сечений будет зависеть от направления интегрирования и от того, прогиб вверх или вниз будет считаться положительным. Так, если начальный угол поворота (угол поворота на одной из опор) будет приводить к растяжению в нижней области, то такой угол поворота может считаться положительным, например, для рассматриваемых нами статически определимых балок основной системы значения углов поворота на обеих опорах могут рассматриваться, как положительные. При действии положительного изгибающего момента углы поворота на опорах также будут положительными.

7. Если к одной из опор статически определимой балки, например опоре В, приложить положительный изгибающий момент, то в это приведет к изменению угла поворота поперечного сечения на опоре В на угол θ_B= Мl/3EI и к изменению угла поворота на опоре А на угол θ_А = Ml/6EI. На рисунке 315.1 для наглядности суммарного взаимодействия показаны отрицательные изгибающие моменты, которые приводят к отрицательным значениям углов поворота, но чтобы не путаться со знаками, изначально значения углов поворота для основной и для вспомогательной систем принимаются положительными.

Например, для двухпролетной балки, показанной на рисунке 315.1, угол наклона между поперечными сечениями балок основной системы будет составлять:

φ_В = qa 3 /24EI +qb 3 /24EI = q(a 3 + b 3 )/24EI (315.1.2)

значение угла наклона на смежной опоре при приложении моментов к балкам вспомогательной системы

φ_В = М_В п a/3EI + M_В л b/3EI = M(a + b)/3EI = Ml/3EI (315.1.3)

φ_В = φ_В + φ_В = q(a 3 + b 3 )/24EI + Ml/3EI = 0 (315.1.4)

M = — q(a 3 + b 3 )/8l (315.1.5)

после этого с учетом опорного момента определяются опорные реакции

A = A + A = qa/2 + M/a = qa/2 — q(a 3 + b 3 )/8la (315.1.6)

C = C + C = qb/2 + M/b = qb/2 — q(a 3 + b 3 )/8lb (315.1.7)

B = B_п + В_л + В_п + В_л = qa/2 + q(a 3 + b 3 )/8la + qb/2 + q(a 3 + b 3 )/8lb (315.1.8)

После того, как расчетные реакции определены, дальнейший расчет выполняется, как для обычной статически определимой балки, вот только необходимо выполнить дополнительные проверки, так прогиб на всех опорах при действующих нагрузках должен быть равен нулю.

При равных пролетах, т.е. при а = b = l/2

φ_В = ql 3 /192EI + ql 3 /192EI = ql 3 /96EI = qa 3 /12 (315.1.9)

φ_В = ql 3 /96EI + Ml/3EI = qa 3 /12EI + 2Mа/3EI = 0 (315.1.10)

M = — ql 2 /32 = — qa 2 /8 (315.1.11)

Опорные реакции составят

A = C = qa/2 — qa/8 = 3qа/8 (315.1.12)

B = 2(qa/2 + qa/8) = 10qa/8 (315.1.13)

Если однопролетная балка имеет одну жестко защемленную опору и шарнирную опору, то такую балку можно рассматривать как двухпролетную неразрезную шарнирно опертую балку, у которой один из пролетов равен нулю и соответственно момент на жестко защемленной опоре будет М = — ql 2 /8, согласно формулы (315.1.5). Это позволяет рассчитывать данным методом не только шарнирно опертые многопролетные балки, но и балки, имеющие жесткое защемление на концах.

2. Трехпролетная балка

При рассмотрении трехпролетной балки у нас появится еще одна неизвестная величина — момент на опоре С:

Рисунок 315.2. Приведение трехпролетной балки к основной и вспомогательным системам

То есть угол наклона между смежными сечениями на опоре В балок вспомогательной системы будет зависеть не только от значения моментов, приложенных на рассматриваемой опоре, но также и от значения момента, приложенного на опоре С. И тогда формула для определения угла наклона на опоре В будет выглядеть так:

φ_В = М_В п a/3EI + M_В л b/3EI — М_С п b/6EI = M_B(a + b)/3EI + M_Cb/6EI (315.2.2)

φ_В = q(a 3 + b 3 )/24EI + M_B(a + b)/3EI + M_Cb/6EI = 0 (315.2.3)

Соответственно для опоры С:

φ_С = q(b 3 + c 3 )/24EI + M_C(b + c)/3EI + M_Bb/6EI = 0 (315.2.5)

Решая систему из двух уравнений (315.4.3) и (315.4.4), можно найти значения моментов на опорах. Например при равных пролетах a = b = c решение задачи значительно упрощается, так как и моменты М_В и М_С, действующие на опорах, при этом будут равными из-за симметричности балки и равномерно распределенной нагрузки:

φ_В = φ_С= qa 3 /12EI + 2Ma/3EI + Ma/6EI = 0 (315.2.6)

5Ma/6EI = — qa 3 /12EI (315.2.7)

M = — qa 2 /10 (315.2.8)

Когда мы решали подобную задачу методом сил, то получили следующие уравнения:

Если мы угол наклона заменим греческой буквой Δ, а статически неопределимые опоры пронумеруем, то уравнения (315.2.3) и (315.2.5) примут вид:

т.е. мало чем будут отличаться от канонических уравнений метода сил.

Если у балки будет 4 пролета, то в итоге мы получим систему из 3 уравнений, в одном из которых будет 3 неизвестных члена, а в первом и последнем — по 2 неизвестных члена. Соответственно для расчетов 5 пролетной балки придется составить систему из 4 уравнений, в двух из которых будет по 3 неизвестных члена, а в первом и последнем также по 2 неизвестных члена, для 6 пролетной — из 5 уравнений и так далее, но при этом количество неизвестных членов в первом и последнем уравнении всегда будет равно двум, а в остальных уравнениях — трем, так как количество моментов, действующих на опорах смежных балок вспомогательных систем, не может быть больше 4. А так как моменты, действующие на рассматриваемой опоре, равны согласно (315.1.1), то количество неизвестных в уравнениях сокращается до 3 и потому уравнения вида (315.2.3) и (315.2.5) называются уравнениями трех моментов.

Для любой многопролетной балки уравнение трех моментов для n-ной опоры можно записать так:

А если обе части уравнения умножить на 6EI, то уравнение трех моментов будет выглядеть так:

где φ_n — рассмотренный нами суммарный угол наклона между смежными сечениями на n-ной опоре.

Произведение φ_nEI иногда для упрощения записи рассматривается, как суммарная фиктивная опора R_n ф :

Физический смысл этой формулы следующий: с точки зрения строительной физики сила, момент, угол поворота и прогиб — это не какие-то случайные понятия, а четко связанные между собой. Например, когда мы определяем опорную реакцию В при действии равномерно изменяющейся нагрузки (от 0 на опоре А до q на опоре В), мы умножаем площадь нагрузки (ql/2) на расстояние от опоры А до центра тяжести этой площади (2/3l) и затем делим это все на длину пролета (l), в итоге В = ql/3, соответственно А = ql/6. А если в качестве грузовой эпюры рассматривать эпюру моментов, также имеющую вид треугольника (например, при моменте, приложенном на опоре В), то значение фиктивных реакций составит В ф = Мl/3, А ф = Ml/6. В общем случае эту закономерность можно отобразить так:

Рисунок 315.3. Определение суммарной фиктивной реакции по эпюрам моментов для балок основной системы.

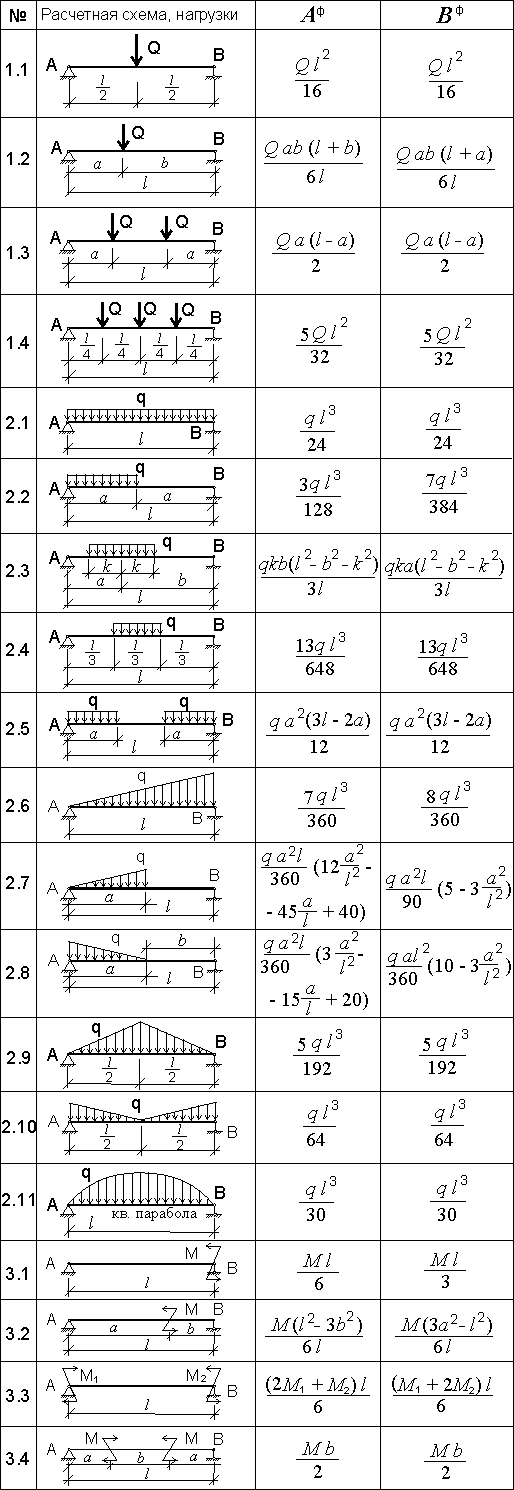
Однако в большинстве случаев чертить эпюры моментов для балок основной системы, затем определять центры тяжести этих эпюр и расстояния до центров тяжести нет большой необходимости, так как для наиболее распространенных вариантов приложения нагрузки фиктивные опорные реакции давно известны и определить их можно по соответствующим таблицам. Пример такой таблицы представлен ниже.

Таблица 315.1. Фиктивные опорные реакции для различных вариантов загружения балки основной системы

4. Решение системы уравнений

После того, как углы поворота на опорах (фиктивные опорные реакции) для всех балок основной системы определены, можно приступать к решению системы уравнений. Вот только, если пролетов у балки много, то запись окончательного уравнения, позволяющего определить один из неизвестных моментов, может занять не одну минуту и не одну страницу. В таких случаях можно воспользоваться следующей методикой:

Для балки, имеющей k пролетов, потребуется составить k — 1 уравнений. Если значения выражений — 6R_n ф заменить параметром c_i, то уравнения будут иметь следующий вид:

(315.4.1)

Если умножить все уравнения на пока произвольные параметры α_i, а затем сложить все левые и правые части уравнений системы (315.4.1), то итоговое уравнение после соответствующих преобразований, позволяющих сократить запись, будет иметь вид:

(315.4.2)

Теоретически множители α могут иметь такие значения, при которых все выражения в квадратных скобках (множители для М_n в формуле (315.4.2)), кроме последнего, будут равны нулю. На основании этого предположения из уравнения (315.4.2) можно составить еще одну дополнительную систему уравнений:

(315.4.3)

Количество уравнений в такой системе будет k — 2, с k — 1 неизвестными параметрами α. Так как число параметров α на единицу больше количества уравнений, то для решения системы значение одного из этих параметров задается произвольно. Наиболее удобным для дальнейших расчетов будет принять значение α₁ = 1. Тогда значения остальных коэффициентов α можно определить, решая систему уравнений (315.4.3):

(315.4.4.1)

(315.4.5)

Примечание: Если придать абстрактным математическим коэффициентам α конкретный физический смысл, то коэффициенты α_n есть не что иное, как такое соотношение моментов на соседних опорах , при котором суммарный угол наклона на рассматриваемой опоре будет равен нулю и тогда эти коэффициенты можно выразить так α_n = M_n/M_n-1. Например, если первое уравнение системы (315.4.1) разделить на М₁, то это уравнение c учетом вышесказанного можно записать так:

(315.4.6)

(315.4.4.2)

После подставления определенных вышеуказанным способом параметров α уравнение (315.4.2) примет вид

(315.4.7)

Соответственно значение М_k-1 будет составлять

(315.4.8)

После этого полученное значение М_k-1 подставляется в последнее уравнение системы (315.4.1) и определяется значение М_k-2. Из предпоследнего уравнения после подставления значений М_k-1 и М_k-2 определяется значение М_k-3 и т.д. Таким образом количество неизвестных в уравнениях системы (315.4.1) сводится к одному.

Если на одном или обоих концах балки есть нагруженные консоли, то определить изгибающие моменты на крайних опорах — не проблема. Значения этих моментов подставляются в уравнение трех моментов, как известные величины, тогда в первом и последнем уравнениях также будет по 3 члена. Если один или оба конца рассчитываемой балки защемлены, то жесткое защемление рассматривается как дополнительный пролет с длиной l = 0, таким образом придется составить еще одно или два уравнения.

5. Уравнение трех моментов для балки с переменной жесткостью:

Когда мы умножали обе части уравнения (315.3.1) на 6EI, то тем самым задавали момент инерции I, как некую постоянную величину. Между тем момент инерции также может быть переменной величиной (например, когда многопролетная железобетонная плита имеет различное армирование в пролетах) и для таких случаев уравнение моментов можно записать так:

(315.5.1)

(315.5.2)

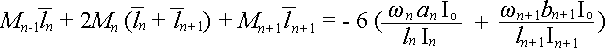
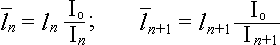
I_o — момент инерции одного из участков балки, принятый за основу.

Вот, в принципе и все теоретические предпосылки для расчета статически неопределимых конструкций методом моментов. А как эту теорию можно применить на практике, рассказывается отдельно.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Категории:

• Расчет конструкций . Статически неопределимые конструкции

Оценка пользователей:9.3 (голосов: 3)Переходов на сайт:26387Комментарии:

Ответьте пожалуйста правильно ли я интерпретирую Вашу статью: Если на одном или обоих концах балки есть нагруженные консоли, то определить изгибающие моменты на крайних опорах — не проблема. Значения этих моментов подставляются в уравнение трех моментов, как известные величины, тогда в первом и последнем уравнениях также будет по 3 члена. Я подставил консоли и получилось, что уравнение (315.4.8) при расчете Трехпролетной балки с консолями должно рассчитываться так: МС = (сВ * ?1 + сС * ?2 — МD * ?3 * ?2 — МА * ?1 * ?1) / (?2 * ?1 + 2 * (?2 + ?3) * ?2) Правильны ли мои выводы?

В целом ваши выводы правильные. Вот только для трехпролетной балки решение может быть проще, так как составляются всего 2 уравнения, а известные значения моментов на крайних опорах переносятся с соответствующим знаком в правую часть уравнений. Таким образом достаточно в первом уравнении выразить МВ через МС, а вторым уравнением найти МС.

Большое спасибо За Вашу работу.

Что такое метод пяти моментов?

Метод пяти моментов используется при расчете многопролетных неразрезных балок на упругоподатливых опорах. Т.е. при расчете дополнительно учитываются возможные деформации таких упругоподатливых опор. В данной статье такая ситуация не рассматривается и вообще это отдельная достаточно большая тема.

«1. Когда мы рассекаем балку на промежуточной статически неопределимой опоре (рис. 315.1.б)), мы получаем две статически определимых балки с общей опорой В» — IMHO они СН тк каждая из балок мешает свободному повороту сечения В соседней балки. Кажется тут небольшая неточность.

А всё понял, извините за глупые замечания

Ничего. Все нормально.

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Расчет неразрезной балки по уравнению трех моментов

Как рассчитать неразрезную балку. Уравнение 3-х моментов.

Неразрезная балка нагружена во всех пролетах. Построить эпюры Q и M для неразрезной балки.

Схема неразрезной балки

1. Определяем степень статической неопределимости балки по формуле:

n= Соп -3= 5-3 =2, где Соп – число неизвестных реакций, 3 – число уравнений статики. Для решения данной балки требуется два дополнительных уравнения.

2. Обозначим номера опор с нулевой по порядку (0,1,2,3)

3. Обозначим номера пролетов с первого по порядку (ι_1,ι_2,ι₃)

4. Каждый пролет рассматриваем как простую балку и строим для каждой простой балки эпюры Q и M. То, что относится к простой балке, будем обозначать с индексом «0», то, что относится к неразрезной балке, будем обозначать без этого индекса. Таким образом, — это поперечная сила и изгибающий момент для простой балки.

Рассмотрим балку 1 го пролета

Определим фиктивные реакции для балки первого пролета по табличным формулам (см.таблицу «Фиктивные опорные реакции. .»)

Балка 2 го пролета

Балка 3 го пролета

5. Составляем уравнение 3 х моментов для двух точек ­­– промежуточных опор ­– опора 1 и опора 2. Это и будут два недостающих уравнения для решения задачи.

Уравнение 3х моментов в общем виде:

Для точки (опоры) 1 (n=1):

Для точки (опоры) 2 (n=2):

Подставляем все известные величины, учитываем, что момент на нулевой опоре и на третьей опоре равны нулю, M₀=0; M₃=0

Тогда получим:

Поделим первое уравнение на сомножитель 4 при M₂

Второе уравнение поделим на сомножитель 20 при M₂

Решим эту систему уравнений:

Из первого уравнения вычтем второе, получим:

Подставляем это значение в любое из уравнений и находим M₂

Итак, нашли опорные моменты:

1. Построение эпюры поперечной силы Q для неразрезной балки

Формула для определения Q в любом сечении неразрезной балки:, где n – пролет

1) Построение эп. Q в первом пролете:

Эта запись означает, что поперечная сила в неразрезной балке в первом пролете будет такая же, как в простой балке с разницей ординат на – 9 .

На эпюрах должны прослеживаться скачки на величину сил.

2) Построение эп. Q во втором пролете:

Поперечная сила в неразрезной балке во втором пролете будет такая же, как в простой балке с разницей ординат на – 9,5.

3)Построение эп. Q в третьем пролете:

Поперечная сила в неразрезной балке в третьем пролете будет такая же, как в простой балке с разницей ординат на +15,3.

Строим эпюру поперечных сил для неразрезной балки.

7. Построение эпюры изгибающего момента для неразрезной балки. Сначала откладываем на опорах значения опорных моментов, соединяем их линией опорных моментов. Это эпюра опорных моментов.

Эпюру М для неразрезной балки можно построить:

1 вариант – методом «подвешивания». К эпюре опорных моментов «подвешиваем» эпюру M 0 по разницам ординат. К примеру, в середине первого пролета на эпюре M 0 ордината равна 90, а на эпюре опорных моментов -27. В итоге получим 90-27=63. Это значение и откладываем.

2 вариант – формула для определения изгибающего M в любом сечении неразрезной балки:

, где n-пролет , x — расстояние.

Для той же точки первого пролета, которую рассматривали в методе «подвешивания»:

Построение эп. М во 2 ом пролете, загруженном равномерно распределенной нагрузкой

Определим положения т. К. по эпюре Q — это точка экстремума.

Определим М неразрезной балки во 2 ом пролете в этой точке: Теперь нужно определить в этой точке К изгибающий момент М в простой балке:

Таким образом, момент в точке К для неразрезной балки:

Строим эпюру М.

8. Выполним проверку опорных реакций. Покажем реакции на схеме балки на опорах, направив их вверх. Значения этих реакций определим по скачкам эпюры Q. Таким образом получим:

Спроецируем все силы, приложенные к балке, и реакции на вертикальную ось, выполним проверку.

Подставим значения, получим 340-340=0

Многопролетные неразрезные балки. уравнение трех моментов

Многопролетные неразрезные балки. уравнение трех моментов

• Многопролетные неразрезные балки. Формула трех моментов Последовательность балок сидит на двух или более опорных петлях в середине. Такие балки широко используются в различных конструкциях и относятся к ряду статически неопределимых. Для риса. На рисунке 414 показана балка, опирающаяся на Т-образный шарнир. Одна из опор является шарнирно-неподвижной для восприятия осевых нагрузок, другая-шарнирно-подвижной, и балка

может свободно изменять свою длину при изменении температуры. Поддержка нумеруется слева направо, указывая самую левую цифру 0.количество пролетов определяется количеством правых опор, которые ему принадлежат. Имейте такую же вертикальную реакцию полагаясь на поддержке шарнира Т. Поскольку существует только два состояния равновесия, такая система (tn—2) статически неопределима. Как видно, число ненужных соединений, а следовательно, и ненужных реакций равно числу промежуточных опор. Иногда крайнее доверие Делается это в виде щепотки.

В этом случае степень статической неопределенности возрастает Людмила Фирмаль

по сравнению с шарнирными опорами. Чтобы получить основную систему, можно удалить все промежуточные опоры и заменить их действие неизвестной реакцией XY x2…In помимо указанной нагрузки, к основной системе прилагается КП-2 (Рис. 415). Дополнительное уравнение перемещения A|=0; A2=0 ″ •••’A/l-2=0 представляет собой условие, равное нулю отклонения в точке крепления промежуточной точки опоры. Но этот метод расчета трудоемкий, 413∞в каждом уравнении перемещения содержатся все неизвестные требуемые силы. Гораздо выгоднее строить основную

систему, размещая шарниры в секциях на всех промежуточных опорах(рис. 416). Ненужные неизвестные в этом случае будут сгибать момент к опоре балки. Таким образом, эквивалентная система представляет собой ряд простых поворотных опорных балок с заданной нагрузкой и неизвестным изгибающим моментом Afj=M2=•>L4l -| — / — HL — / — b • • •» Рис четыреста пять Применяется в секции, где установлен шарнир. Предполагается, что направление момента для определенности является положительным. Если выбрана эта основная система, указанное поведение нагрузки

• применяется только к пролету, на котором оно применяется; Четыреста шестнадцать риса Рис сорок семь Другой пролет ее ПА представлен опорным изгибающим моментом M(. Теперь сформулируем дополнительное уравнение перемещения. Они выражают равенство нулю смещения опорной части в направлении действия МЗ в неизвестный момент времени. Фактически каждая вторичная опорная балка основной системы под действием заданной нагрузки и опорного момента деформируется независимо от других. Это конец двух соседних Бало-чек, примыкающих к одной из опор, например, р-й(рис. 417), может поворачивать D G и D «º a» на определенный угол. В исходной статически неопределенной

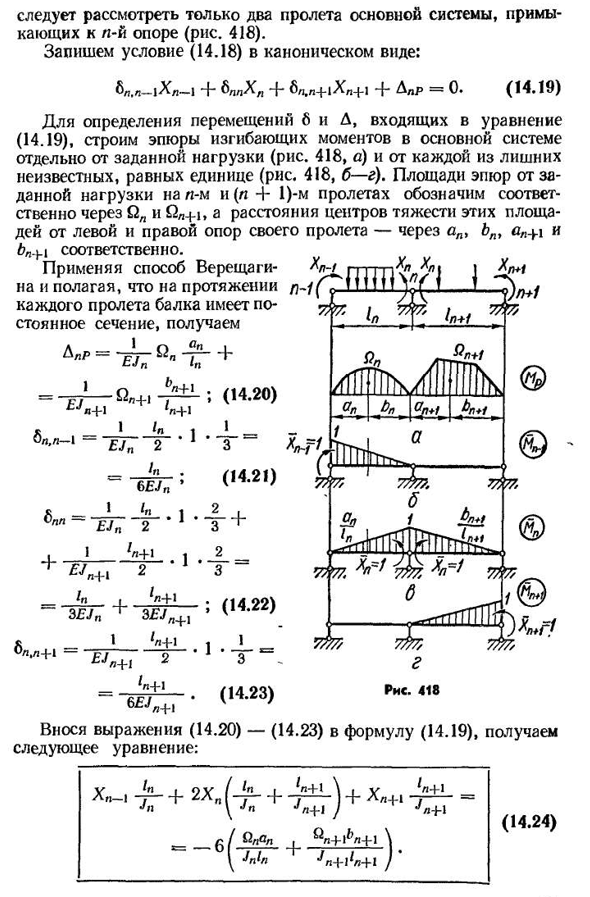
системе каждая пара таких секций представляет собой одну секцию, так что их взаимный угол поворота из непрерывного условия равен нулю, следовательно, каждая промежуточная опора D » =D G4-D G B=0. (14.18) Поскольку основная система состоит из двух несущих балок, независимых и не связанных между собой, то для раскрытия условий(14.18)) Необходимо рассмотреть только два пролета основной системы, Соединенных с 414n-й опорой(рис. 418). Запишите условие(14.18) в каноническом виде:^p. n-jXn-1+6P «xya4-6P», 4-1HP+1+LPR=0. (14.19) для определения перемещений, входящих в уравнение (14.19) 6 и D, постройте график изгибающих моментов основной системы отдельно от заданной нагрузки

(фиг. 418, С) и от каждого из дополнительных неизвестных, равных Людмила Фирмаль

единице(рис. 418, б-д). Площадь участков n-m и (l+1)-m пролета от заданной нагрузки соответственно через Q»и Q»+i, а расстояние центра тяжести этих участков, его пролет-через AP, BP-соответственно. Если применить метод Верещагина и предположить, что балка имеет определенное поперечное сечение на протяжении каждого пролета、 ^p’P

2 1—- k_ J ВЯ _ П2 3Р■а±л. Джей, 2=2 3 ЛН+л 3jn+л Если вы добавите 1ci-H n+i2=6£7L+1 выражение (14.20)—(14.23) к выражению (14.19: ^1 и Я ЛН+т ф НН ЭДЖ+ — £Т- _ /» 3jn 6/м-н — £Дж + В/н т^н+ф Лето bn+1 (14.22) (14.23) мы самые лучшие! (14.20 утра)) Zn+I М и1. ■ 1 — ’ т — & Х», Л — +2Х» Джей Н Я в-н+^»Г Л Л-Н——•’»4-1 (14.24) 415 при таком выборе основной системы все лишние неизвестные находятся в Формуле (14.24), она принимается вместо X и изгибает момент к опоре балки.、- И так оно и есть., (14.25))

Выражение (14.25) называется выражением трех моментов. Мы вводим петли, чтобы сформировать основную систему. Чтобы записать эти уравнения, достаточно в Формуле (14.25) дать индексу Р последовательно значения 1,2, 3 и т. д., Соответствующее числу промежуточных опор. Каждое из этих уравнений содержит три и более неизвестных опорных момента L1p], m», а также первое и последнее уравнения, и не более того-только решения этих двух систем легко выполнить методом последовательного устранения неизвестных. М н-iln4

ЛН+л)+= Л-С-Л-С’»+»)’ (14.26) Рассмотрим пример составления уравнения из трех моментов. Для риса. 419 показывает двухпролетную балку. Система не однажды определяется статически. Промежуточная помощь сразу же, что было моментом уравнения/. Если принять выражение (14.26)n=1, то существует M olt+2L4, (/,+/2)+M2/2=-6. (14.27) поскольку крайняя

левая опора шарнирно закреплена и не нагружена сосредоточенным крутящим моментом, МО=0. 416moment крайней правой концевой опоры равно времени нагрузки, приложенной к консоли. И так оно и есть., Lll12-2. Очевидно. / 1=л-п КР; г ф т+ф; / *2 —- • а т М,=4-П -^ =- г (//+с):= О-2 — b » 2 3 8 12 12 * _ /, Два. • Таким образом, выражение (14.27) принимает вид. ’з++Т’ А2 = Б2= -±- Шесть. / Ped4+с6л Зет Два.. Отсюда легко найти moment/I1. Если левый край балки защемлен(рис. 420, а) могут быть заменены дополнительными пролетами с бесконечно большой жесткостью, защемлением или бесконечно малым пролетом для 1-й и 2-й опор следующим образом( (/, + /2) + ^2^2 == =К2=0; Длина (рис. 420, б). Уравнение б Четыреста

двадцать риса Mj / g4-2L12 (^2+^z)L1z / 3 — = — 6 Очевидно. УГ=*3 = −7 — ; Кроме того, нужно поставить=0 в первое уравнение системы. Затем +2L42(Z2+Z3) −6. Аналогично, если правый край балки защемлен. 14 8-2770 417 опорные моменты, расчет реакций, построение фигур изгибающих моментов и боковых сил обычным способом. Сначала определите реакцию опоры каждой простой балки от заданной нагрузки и опорного момента. Мы показываем эти реакции на l-й полет через AP и VP(рис. 421, а). Это очевидно А-Л° — Л М Н-М Н-1. Мне 7 лет. » * л ВП-в°-р-м р ^ м^, (14.28) * л Вот, » — только реакция от определенной нагрузки на пролет. Полная реакция промежуточного носителя Р (фиг. 421, б» В; — в»+L._,-/g; — MP-m,.

(Йорк) Где Rn=VP+ — реакция опоры l, вызванная действием заданной нагрузки, добавленной к пролету 1P и/l+]. После определения реакции постройте график Q и M для каждой второй опорной балки основной системы. Окончательный график изгибающего момента также легко построить как сумму графика момента от нагрузки и опорного момента, последний график не поддерживается. Можно рекомендовать следующие шаги для расчета непрерывного луча. После опоры и нумерации пролетных строений (опора-от нуля, пролет-от единицы) основной Сит устанавливают под начальную балку и нагружают базовыми моментами неизвестного тогда участка только М от конкретной нагрузки на пролет, для отдельных балок основной системы. Вычислите площадь Qi этих участков и ai9B

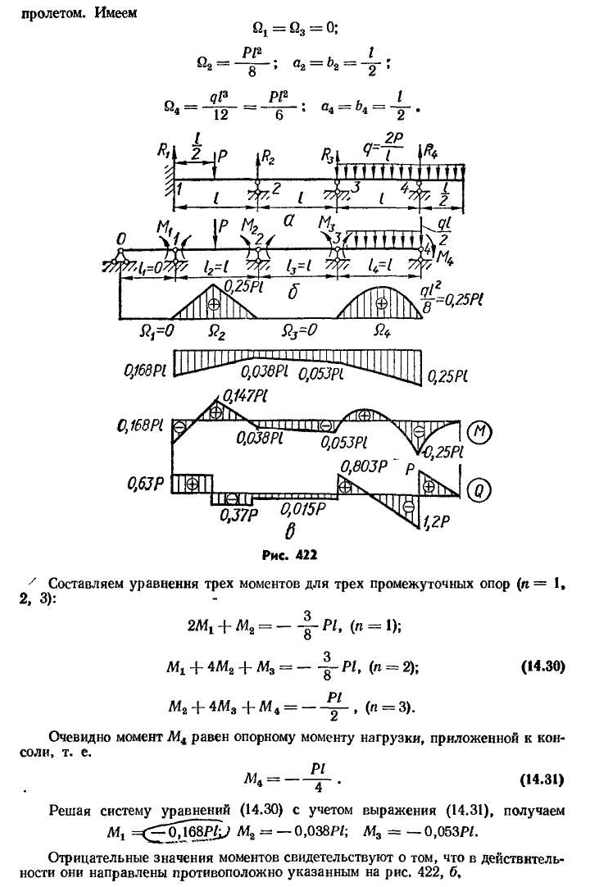
(координату их центроида. Выпишите три мгновенных уравнения для каждой промежуточной опоры. Решая полученную таким образом систему уравнений, определяется неизвестный опорный момент. Затем определяют реакцию, строят график боковых сил и изгибающих моментов. Как показано, последний график может быть построен как сумма моментов нагрузки и моментов опоры. 68, например. График изгибающего момента и поперечной силы балки показан на рисунке. 422, A. 2P Для простоты расчета используется q= — p. эти системы показаны. 422, б, зажим левого конца балки заменить дополнительным У 418 пролетом 7 составьте уравнение трех

моментов для трех промежуточных точек опоры (n=1. Три.): 2Mt+L1A= — П/, (Л=1);т+4ма+м3= — я, (» = 2); (14.30) мг+4/и3+М4=- — — — — (П=3). Очевидно, что момент M4 равен опорному моменту нагрузки, приложенной к КС-соли. МТ= — — — — — — (14.31) Принимая во внимание формулу для решения системы уравнений (14.30) (14.31), M1=

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

💡 Видео