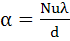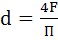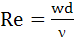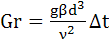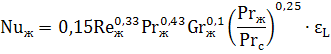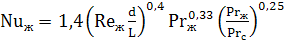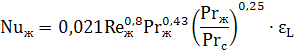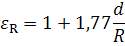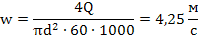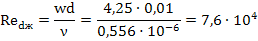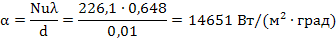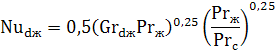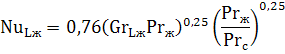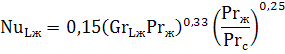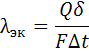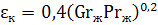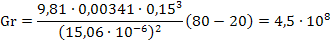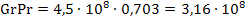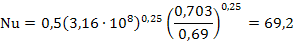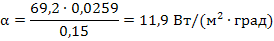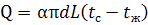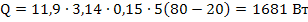Уравнения теплоотдачи для воздуха при свободной конвекции

Федеральное государственное бюджетное образовательное учреждение

«Ростовский государственный университет путей сообщения»

(ФГБОУ ВПО РГУПС)

Определение коэффициента теплоотдачи

при свободной конвекции

2012

Определение коэффициента теплоотдачи при свободной конвекции (метод струны) : учебно-методическое пособие к лабораторной работе / , , ; ФГБОУ ВПО РГУПС. – Ростов н/Д, 2012. – 14 с. : ил.

В данном пособии приводятся методические указания к лабораторной работе по определению коэффициента теплоотдачи при свободной конвекции (метод струны).

Предназначено для студентов специальности 140104 – «Промышленная теплоэнергетика», 190300.65 – «Подвижной состав железных дорог».

Одобрено к изданию кафедрой «Теплоэнергетика на железнодорожном транспорте» РГУПС.

Рецензент канд. техн. наук, доц. И. Н. Жигулин (РГУПС)

© ФГБОУ ВПО РГУПС, 2012

Современные энерготехнологические системы требуют от специалиста глубокого понимания законов и принципов действия теплового оборудования, встроенного в эти системы. Только достаточно высокий уровень общетеплотехнической подготовки позволит специалисту решать задачи по созданию современных экономически выгодных тепловых установок и находить пути повышения их энергетической эффективности.

Лабораторные исследования позволяют более глубоко понимать основные законы термодинамики и теплопередачи, принципы работы тепловых установок. Обработка опытных данных может осуществляться с помощью диаграмм и справочных таблиц, умение пользоваться которыми необходимо инженеру.

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛООТДАЧИ

ПРИ СВОБОДНОЙ КОНВЕКЦИИ

Цель работы. Определение экспериментальным путем на лабораторной установке коэффициента теплоотдачи при свободной конвекции в неограниченном пространстве. Изучение методики обработки опытных данных с применением теории подобия и составления критериального уравнения по результатам эксперимента.

Основные положения. Теплообмен в условиях естественной конвекции осуществляется при местном нагревании или охлаждении среды, находящейся в ограниченном или неограниченном пространстве. Этот вид конвективного переноса тепла играет преимущественную роль в процессах отопления помещений и имеет значение в различных областях техники. Например, нагревание комнатного воздуха отопительными приборами, а также нагревание и охлаждение ограждающих конструкций помещений (стены, окна, двери и пр.) осуществляется в условиях естественной конвекции или так называемого свободного потока.

Естественная конвекция возникает в неравномерно нагретом газе или жидкости, находящейся в ограниченном или неограниченном пространстве, и может влиять на конвективный перенос тепла в вынужденном потоке среды. В больших масштабах свободное перемещение масс среды, вызванное различием ее плотностей в отдельных местах пространства, осуществляется в атмосфере земли, водных пространствах океанов и морей и т. д.

За счет естественного движения нагретого воздуха в зданиях осуществляется его вентиляция наружным воздухом. Исследованием свободной конвекции занимался еще , который применял подъемную силу нагретых масс воздуха для устройства вентиляции шахт, а также для перемещения газов в пламенных печах. К настоящему времени достаточно полно изучен естественный конвективный теплообмен для тел простейшей формы (плита, цилиндр, шар), находящихся в различных средах, заполняющих пространство бόльших размеров по сравнению с размерами самого тела.

Как показывает опыт, характер свободного течения среды относительно поверхности нагретого тела бывает как ламинарным, так и частично или полностью турбулентным.

Рис. 1. Характер течения среды

у вертикального цилиндра

На рисунке 1 показано свободное перемещение комнатного воздуха у вертикально подвешенной нагретой трубы большой длины. На нижнем участке трубы наблюдается ламинарное течение воздуха вверх. На некотором расстоянии от нижнего конца трубы перемещение слоев воздуха теряет ламинарный характер, возникают отдельные локонообразные массы, появляются искривленные струйки, которые далее дробятся на более мелкие, и восходящий поток воздуха у нагретой трубы приобретает турбулентный характер с ламинарным пристенным слоем. Рисунок 1 является хорошей иллюстрацией развития и перехода ламинарного течения в турбулентное.

Экспериментально коэффициент теплоотдачи может быть определен из основного уравнения теплоотдачи Ньютона – Рихмана

, (1)

где Q – мощность теплового потока, передаваемого свободной конвекцией в окружающую среду;

F – теплоотдающая поверхность;

Δt – температурный напор (разность температур между теплоотдающей средой и окружающей средой).

Свободный конвективный теплообмен тел в различных средах, находящихся в неограниченном пространстве, экспериментально изучался различными исследователями. Опыты проводились с телами простейшей формы (плиты, цилиндры, шары) с размерами от 15 мм (проволоки) и до 16 м (шары) в различных средах (различные газы и жидкости).

Результаты исследований обобщались с помощью характерных для этого явления критериев Nu (Нуссельта), Gr (Грасгофа) и Рr (Прандтля), что находится в полном соответствии с теорией подобия и аналитическим решением задачи. Изменение физических параметров в пограничном слое удается учесть введением критериального отношения, представляющего относительное изменение параметров переноса ν и а в пределах изменения температуры среды: tп − температур потока окружающей среды, tст − температуры среды на границе со стенкой.

Академиком и , на основании обобщения результатов экспериментального исследования, рекомендуются следующие формулы для расчета средних критериев теплообмена тел в свободном потоке.

Для горизонтальных труб в диапазоне изменения Gr · Pr от 103 до 108:

, (2)

где − средний критерий Нуссельта;

− критерий Грасгофа;

− критерий Прандтля при температуре потока окружающей среды;

− критерий Прандтля жидкости при температуре среды на границе со стенкой.

Для вертикальных труб и плит в диапазоне изменения Grп,h · Рrп от 103 до 109 (что отвечает ламинарному течению среды):

, (3)

и в диапазоне изменения Grп, h Рrп > 109 (что отвечает турбулентному течению):

. (4)

Для газов отношение мало зависит от температуры, и его можно принять за 1.

Формула (4) для расчета критерия конвективного теплообмена в условиях естественной конвекции при турбулентном режиме течения характерна тем, что коэффициент теплоотдачи оказывается не зависящим от размера тела.

Для тонких проволок малого размера, для которых выполняется условие (Grп, d · Prп) 2 · 107

Численные значения коэффициента С и показателя степени n в формуле (6) можно принять по таблице

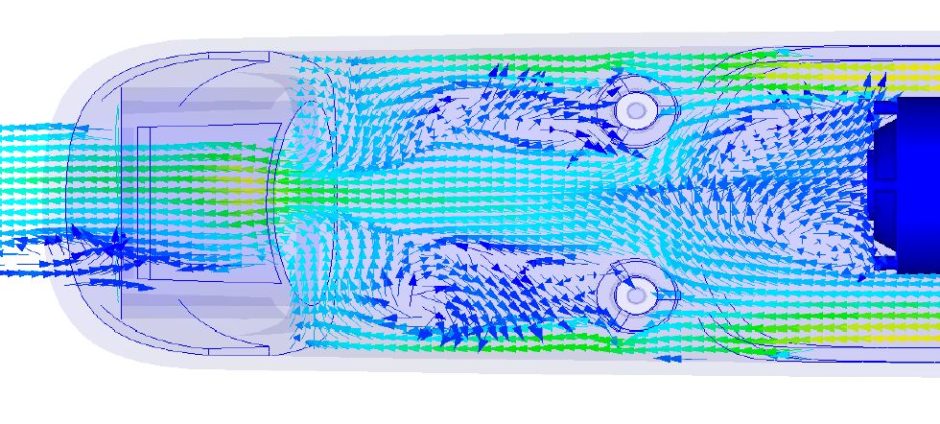
Рис. 2. Схема лабораторной установки

Схема и описание установки. В экспериментальной лабораторной установке (рис. 2) теплоотдающей стенкой является нихромовая проволока 3 (струна) длиной 1540 мм и диаметром 0,5 мм, по которой пропускается электрический ток напряжением до 30 В. Таким образом, размеры струны определяют теплоотдающую поверхность F = 2,419 · 10–3, м2. Струна удерживается в вертикальном положении стойкой 1 с двумя кронштейнами. В верхнем кронштейне 2, изолированном от массы установки, неподвижно закреплен один конец струны. Другой конец струны зажат в головке индикатора часового типа 5. Головка индикатора свободно перемещается в изоляторе-держателе 4 нижнего кронштейна. Груз 6 обеспечивает постоянное по величине натяжение струны. Напряжение от сети 220 В подводится через автотрансформатор к держателю 2 и головке индикатора 5. Для определения мощности теплового потока служат вольтметр 7 и амперметр 8.

Все результаты измерений заносятся в протокол наблюдений (табл. 1) при стационарном режиме. О стационарности режима можно судить по неизменности показаний индикатора удлинения струны, т. е. по постоянству температуры струны.

Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах

Теплоотдача при вынужденном течении жидкости в трубах и каналах

Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).

При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.

Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).

Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м 2 ·град), который определяется по формуле:

Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, равный

F – площадь сечения канала, м 2 ; П – периметр канала, м.

Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.

В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.

Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.

• Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
• При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
• Турбулентный режим течения в трубах наблюдается при числах Re более 10000.

Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).

Число Re определяется по формуле:

w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м 2 /с.

Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.

Теплоотдача при ламинарном течении в трубах и каналах

Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.

Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.

g – ускорение свободного падения, м/с 2 ;

β – температурный коэффициент объемного расширения, град -1 ;

d – эквивалентный диаметр канала, м;

ν — кинематическая вязкость жидкости при средней температуре, м 2 /с;

Δt – средняя разность температур жидкости и стенки, °С.

Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10 5 , то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:

Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.

Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки.

ε_L – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:

Значения коэффициента ε_L при ламинарном режиме

L/d	1	2	5	10	15	20	30	40	50
εL	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1

Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr 5 , влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:

d – эквивалентный диаметр канала, м;

L – длина трубы (канала), м.

Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:

λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, м.

Теплоотдача в трубах и каналах при турбулентном режиме

Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:

Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Pr_с берется при температуре стенки.

Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10 4 до 5·10 6 и Pr от 0,6 до 2500.

ε_L – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения ε_L приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:

Значения коэффициента ε_L при турбулентном режиме

Reж	L/d
	1	2	5	10	15	20	30	40	50
1·10 4	1,65	1,5	1,34	1,23	1,17	1,13	1,07	1,03	1
2·10 4	1,51	1,4	1,27	1,18	1,13	1,1	1,05	1,02	1
5·10 4	1,34	1,27	1,18	1,13	1,1	1,08	1,04	1,02	1
1·10 5	1,28	1,22	1,15	1,1	1,08	1,06	1,03	1,02	1
1·10 6	1,14	1,11	1,08	1,05	1,04	1,03	1,02	1,01	1

Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:

R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.

Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.

Расчет теплоотдачи при вынужденной конвекции

Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды t_ж=50°С, температура стенки трубы t_с=10°С.

1. Определим физические свойства воды при температуре 50°С:

• Теплопроводность воды λ_ж= 0,648 Вт/(м·град);
• Плотность воды ρ_ж=988 кг/м 3 ;
• Кинематическая вязкость воды ν_ж=0,556·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=3,54;
• Число Прандтля при температуре стенки Pr_с=9,52.

2. Рассчитаем среднюю скорость течения воды w по трубе:

3. Определим число Рейнольдса Re:

4. Поскольку число Рейнольдса имеет значение больше 1·10 4 , то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:

Определим коэффициент ε_L по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент ε_L=1_.

Выполним расчет числа Нуссельта по приведенному критериальному уравнению:

5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:

Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м 2 ·град).

Теплоотдача при свободной конвекции в трубах и каналах

Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.

Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).

Свободная конвекция в неограниченном пространстве

Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.

Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:

В качестве определяющего размера принимается наружный диаметр d канала или трубы.

Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:

При GrPr>10 9 :

Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.

Свободная конвекция в ограниченном объеме

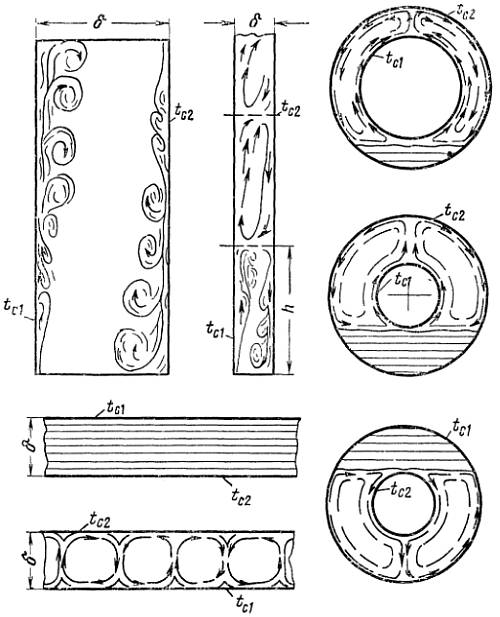
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.

Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λ_эк.

Эквивалентный коэффициент теплопроводности определяется по формуле:

Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м 2 ; Δt=t_c1-t_c2 — температурный напор между нагретой и холодной стенками, °С.

Отношение эквивалентного коэффициента теплопроводности λ_эк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции ε_к, который определяется значением комплекса GrPr.

При малых значениях комплекса GrPr 3 6 :

При 10 6 10 :

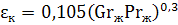
Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной t_ж=0,5(t_c1+t_c2). В качестве определяющего размера принимается δ — толщина слоя жидкости.

Расчет теплоотдачи при свободной конвекции

Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки t_с=80°С. Температура окружающего воздуха t_ж=20°С.

1. Определим физические свойства воздуха при температуре 20°С:

• Теплопроводность воздуха λ_ж= 0,0259 Вт/(м·град);
• Кинематическая вязкость воздуха ν_ж=15,06·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=0,703;
• Число Прандтля при температуре стенки Pr_с=0,69;
• Коэффициент объемного расширения β_ж=1/(273+20)=0,00341 град -1 .

2. Вычислим число Грасгофа Gr по формуле:

3. Определим значение комплекса GrPr:

Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:

4. Вычислим значение числа Нуссельта Nu:

5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:

6. Определим потери тепла с боковой поверхности трубопровода по формуле:

Подставляя численные значения, окончательно получаем потерю тепла:

Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.

Коэффициент теплоотдачи поверхность — воздух

В статье рассмотрен расчет мощности теплового потока от горизонтальных и вертикальных плоских поверхностей тела, помещенного в «безразмерное» воздушное пространство при принудительной и естественной конвекции с учетом радиационной составляющей теплоотдачи.

Зная коэффициент теплоотдачи на поверхности (α), разделяющей твердое тело и окружающее это тело воздушное пространство, очень просто определить мощность теплового потока (Q) по известной разности температур (Δt).

Q=α*A*Δt, Вт – мощность теплового потока от или к поверхности тела.

• α=α_к+α_р, Вт/(м 2 *К) – суммарный коэффициент теплоотдачи на границе воздух – поверхность тела
  • α_к=?, Вт/(м 2 *К) – коэффициент конвективной теплоотдачи
  • α_р=ε*5,67*10 -8 *((t_п+273,15) 4 — (t_в+273,15) 4 )/(t_п-t_в)), Вт/(м 2 *К) – коэффициент радиационной теплоотдачи (теплоотдачи излучением), ε – степень черноты поверхности
• А, м 2 – площадь поверхности
• Δt=|t_п-t_в|, К – разность температур поверхности и воздушной среды
  • t_п, °C – температура поверхности
  • t_в, °C – температура воздуха

Основная сложность расчета заключается в определении коэффициента конвективной теплоотдачи (α_к)! Автоматизировать в первую очередь решение этой трудоемкой задачи поможет Excel.

Нестабильность процесса естественной конвекции у поверхностей различной формы и расположения в пространстве породила большое разнообразие эмпирических формул для вычисления коэффициента конвективной теплоотдачи (α_к). Неизбежные погрешности экспериментальных данных привели к тому, что результаты вычислений для одних и тех же поверхностей и условий по формулам разных авторов отличаются друг от друга на 20% и более.

После тщательного детального ознакомления с материалами современных западных изданий по теплообмену (список литературы – в конце статьи) были выбраны формулы, рекомендованные к применению большинством авторов, для использования в представленной далее программе в Excel.

Схемы теплообмена:

На представленных ниже рисунках показаны 8 вариантов схем, для которых программа может выполнить вычисления.

Розовый цвет пластин свидетельствует о том, что они горячее окружающего воздуха. Голубой цвет – пластины холоднее воздуха.

На схемах 1а и 1б воздух принудительно движется (вентилятор, ветер) вдоль поверхности пластины независимо от её ориентации в пространстве. На всех остальных схемах окружающий воздух находится в спокойном состоянии (помещение, полный штиль), а положение пластин сориентировано в пространстве.

Расчет в Excel:

Формулы алгоритма программы:

t₀=(t_в+t_п)/2

l₀=L – для схем 1а и 1б

l₀=(B*L)/(2*(B+L)) – для схем 2а, 2б, 3а, 3б, 4а, 4б

Для определения теплофизических параметров воздуха при определяющей температуре (t₀) в диапазоне -70°C … +1200°C использованы формулы из предыдущей статьи на сайте.

Re=w*l₀/ν

Gr=g*β*|t_п— t_в|*l₀ 3 /ν 2

Ra=Gr*Pr

α_к=Nu*λ/l₀

α_р=ε*0,00000005670367*((t_п+273,15) 4 — (t_в+273,15) 4 )/(t_п-t_в)) – при t_в *) α_р=0 – при t_в>t_п

α=α_к+α_р

q=α*(t_п-t_в)

Q=q*B*L

*) Нагрев поверхностей Солнцем или иными источниками теплового излучения программой игнорируется.

Вычисление теплофизических параметров воздуха и числа Нуссельта, как видно из вышеприведенных формул, являются ключевыми и самыми трудоемкими при определении конвективного коэффициента теплоотдачи.

Тестирование программы проводилось на примерах из книг, представленных в конце статьи. Отклонения результатов в основном не выходили за пределы ±5%.

Замечание:

В отечественной теплотехнической литературе для решения рассмотренных задач широко используются формулы второй половины прошлого века М.А. Михеева и В.П. Исаченко, которые в современной западной литературе не упоминаются. Беглый сравнительный анализ результатов расчетов по формулам разных авторов дал противоречивые и неоднозначные ответы. Если при принудительной конвекции результаты фактически идентичны, то при естественной конвекции отличаются порой на 30% и более, но иногда почти совпадают…

Литература:

1. John H. Lienhard IV, John H. Lienhard V, A Heat Transfer Textbook (Fifth Edition), 2019.
2. Frank Kreith, Raj M. Manglik, Mark S. Bohn, Principles of heat transfer (Seventh Edition), 2011.
3. Adrian Bejan, Convection Heat Transfer (Fourth Edition), 2013.
4. Michel Favre-Marinet, Sedat Tardu, Convective Heat Transfer, 2009.
5. Harlan H. Bengtson, Convection Heat Transfer Coefficient Estimation, 2010.
6. Rajendra Karwa, Heat and Mass Transfer, 2017.
7. Stuart W. Churchill, Humbert H. S. Chu, Correlating equations for laminar and turbulent free convection from a vertical plate, International Journal of Heat and Mass Transfer, Volume 18, Issue 11, November 1975.
8. http://people.csail.mit.edu/jaffer/SimRoof/Convection/
9. И. И. Кирвель, М. М. Бражников, Е. Н. Зацепин ЭНЕРГОСБЕРЕЖЕНИЕ В ПРОЦЕССАХ ТЕПЛООБМЕНА, 2007.

Прошу уважающих труд автора скачать файл с программой после подписки на анонсы статей!

P. S. (01.11.2020)

Дополнение по естественной конвекции у вертикальной поверхности:

Если построить графики по вышеприведенным формулам Черчилля и Чу для числа Нуссельта при естественной конвекции у вертикальной изотермической поверхности (схемы 2а и 2б), то можно увидеть, что при Ra=10 9 кривые не совпадают!

По этому поводу авторы формул Черчилль и Чу дают примерно следующее пояснение: «уравнение, основанное на исследованиях Черчилля и Усаги Nu=(0,825+0,387*Ra 1/6 /(1+(0,492/Pr) 9/16 ) 8/27 ) 2 дает хорошие результаты для средней теплопередачи при свободной конвекции у изотермической вертикальной пластины во всем диапазоне значений Ra и Pr от 0 до ∞, даже если оно не работает для обозначения дискретного перехода от ламинарного к турбулентному потоку». Линхарды в [1] отмечают, что рассматриваемое уравнение чуть менее точно для ламинарных условий при Ra 9 и рекомендуют в этом диапазоне использовать первое уравнение тех же авторов Nu=0,68+0,67*Ra ¼ /(1+(0,492/Pr) 9/16 ) 4/9 . Хотя, судя по графикам, в диапазоне Ra 7 для воздуха обе функции чрезвычайно близки друг к другу.

Еще один нюанс, который встретился только у Линхардов в [1]: «свойства флюида следует оценивать при t₀=(t_в+t_п)/2 за одним исключением, если флюид – газ, то коэффициент объемного расширения β следует определять при t₀=t_в». Но сами авторы зависимостей Черчилль и Чу о таком условии ничего не пишут. По этому поводу в их статье [7], говорится, что «для больших температурных перепадов, когда физические свойства существенно различаются, Ид рекомендует оценивать физические свойства как средние значения температуры поверхности и объема, а Уайли дает более подробные теоретические указания для режима ламинарного пограничного слоя».

Максимальная относительная ошибка для Nu=(0,825+0,387*Ra 1/6 /(1+(0,492/Pr) 9/16 ) 8/27 ) 2 , если β=1/t_в вместо β=2/( t_в+t_п), составляет в процентах:

ε=(((t_в+t_п)/(2*t_в)) 1/3 -1)*100%, или

ε=((|(t_п— t_в)|/(2*t_в)+1) 1/3 -1)*100%

Как видно из графика при температуре среды — воздуха t_в=20°C=293,15K и при перепаде температур поверхности и воздуха Δt=|t_п— t_в| 90 °C расхождение результатов быстро нарастает.

Правы Линхарды или множество других авторов, рассчитывающих все свойства флюидов при одном значении определяющей температуры t₀=(t_в+t_п)/2? Однозначного ответа у меня нет.

(По материалам Обри Джаффера [8].)

Эмпирические уравнения для суммарного коэффициента теплоотдачи:

В инженерных расчетах для быстрого приближенного определения суммарного коэффициента теплоотдачи, учитывающего и конвекцию, и излучение на границе поверхность тела – среда, можно использовать более простые зависимости, приведенные в [9].

При расчете тепловых потерь через наружные поверхности тел, которые находятся в спокойном воздухе закрытых помещений, можно применить нижеприведенные формулы. Результаты вычислений по этим формулам достаточно близки к результатам более точных расчетов.

α=9,74+0,07*(t_п-t_в), Вт/(м2*°C) при t_п On-line калькуляторы для расчетов коэффициентов конвективной теплоотдачи от плоских, цилиндрических и сферических поверхностей:

Инструменты представлены Группой исследований теплопередачи (HTRG). Группа была создана в 2014 году преподавателями Лаборатории теплотехники и жидкостей факультета машиностроения инженерной школы Сан-Карлоса (EESC) Университета Сан-Паулу (USP) для проведения передовых, качественных фундаментальных и прикладных исследований по вопросам теплопередачи для многофазных и однофазных систем.

Точность результатов вычислений не проверял.

💥 Видео