Уравнения температурной зависимости теплоемкости вещества (2 видео)

Содержание

Интерполяционные уравнения, описывающие температурную зависимость теплоемкости
Зависимость теплоемкости от температуры
Уравнения температурной зависимости теплоемкости вещества
🌟 Видео

Видео:Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Интерполяционные уравнения, описывающие температурную зависимость теплоемкости

Модуль 2 Лекция 5

Понятие о теплоёмкости. Теории теплоёмкости газа и конденсированных тел. Методы её оценки на основе экспериментальных данных. Зависимость теплоёмкости от температуры. Зависимость теплового эффекта от температуры и давления. Формула Кирхгофа. Квантовая теория теплоемкости Эйнштейна и Дебая. Понятие о характеристической температуре и методы её оценки на основе экспериментальных данных. Экспериментальные методы исследования теплоёмкости.

Зависимость теплового эффекта реакции от температуры.
Закон Кирхгоффа

В общем случае тепловой эффект химической реакции зависит от температуры и давления, при которых проводится реакция. Влиянием давления на ΔН и ΔU реакции обычно пренебрегают. Влияние температуры на величины тепловых эффектов описывает закон Кирхгоффа:

· Температурный коэффициент теплового эффекта химической реакции равен изменению теплоемкости системы в ходе реакции, т.е. равен разности сумм теплоемкостей продуктов реакции и сумм теплоемкостей исходных веществ..

Продифференцируем ΔН и ΔU по температуре при постоянных давлении и температуре соответственно:

(5.1)

(5.2)

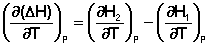
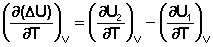
Производные энтальпии и внутренней энергии системы по температуре есть теплоемкости системы в изобарных и изохорных условиях C_p и C_v соответственно:

(5.3)

(5.4)

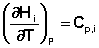
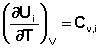
Подставив выражения (5.3, 5.4) в (5.1, 5.2), получаем математическую запись закона Кирхгоффа:

(5.5)

(5.6)

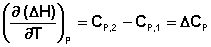
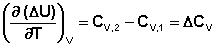
Для химического процесса изменение теплоемкости задается изменением состава системы и рассчитывается следующим образом:

(5.7)

(5.8)

Если проинтегрировать выражения (5.5, 5.6) от Т = Т₁ до Т = Т₂, считая ΔС_p (ΔС_v) не зависящим от температуры, получим интегральную форму закона Кирхгоффа:

(5.9)

(5.10)

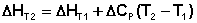
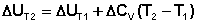
Поскольку обычно известны табличные значения стандартных тепловых эффектов ΔН°₂₉₈ и ΔU°₂₉₈, преобразуем выражения (5.9, 5.10):

(5.11)

(5.12)

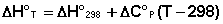
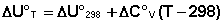
При расчете изменения теплового эффекта реакции в большом интервале температур необходимо учитывать зависимость теплоёмкости от температуры, которая выражается степенным рядом

C°_p = a + bT + c׳ T -2 (для неорганических соединений);

C°_p = a + bT + cT 2 (для органических соединений);

коэффициенты a, b, c приведены в справочниках. Следует отметить, что если ΔC_p > 0, то с увеличением температуры растет также и тепловой эффект, а если ΔC_p

(5.13)

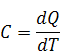
Различают теплоемкость при постоянном давлении C_p (изобарную) и при постоянном объеме C_v (изохорную). Взаимосвязь этих теплоемкостей для идеальных газов определяется соотношением:

где R – универсальная газовая постоянная, равная 8,314 Дж/моль К.

Из кинетической теории газов вытекает, что внутренняя энергия (U) одноатомного идеального газа равна:

При повышении температуры одноатомного газа на 1 градус изохорная теплоемкость будет равна:

ΔU = U_T+1 – U = 3/2 R (T + 1) – 3/2 RT = 3/2 R, (5.16)

а изобарная теплоемкость

C_p = C_v + R = 3/2 8,314 + 8,314 = 20,789 Дж/моль К. (5.17)

Изобарная и изохорная теплоемкости для твердых и жидких веществ достаточно близки, т.е. с повышением температуры изменение объема последних незначительно.

При расчете теплоемкости следует учитывать, что молекулы одноатомного газа имеют три степени свободы движения атомов в трехмерном пространстве, а двухатомного газа – пять степеней свободы: 3 степени поступательного движения и 2 – вращательного.

Это остается верным для любых линейных многоатомных молекул. Для нелинейных молекул трехатомного газа, а также для молекул более сложного строения, т.е. многоатомных, появляется еще одна степень свободы вращательного движения. Следует отметить, что на каждую степень свободы молекулы при поступательном и вращательном движениях приходится в пересчете на 1 моль газа энергия, равная ½ RT. Отсюда, принимая во внимание известное соотношение (5.15), можем найти теплоемкость при постоянном давлении C_p: для одноатомного газа она равна 5/2R или 20,8 Дж/моль К, а суммы поступательного и вращательного вкладов двухатомных и многоатомных линейных молекул в пересчете на моль идеального газа соответственно равны:

C_p = C_v + R = 5/2R + R = 29,1 Дж/моль К. (5.18)

C_p = C_v + R = 3R + R = 33,26 Дж/моль К. (5.19)

Однако, экспериментальные значения теплоемкости двухатомных и многоатомных газов отличаются от расчетных значений (5.18) и (5.19), т.к. имеют еще дополнительную колебательную составляющую; полное значение изобарной теплоемкости идеальных газов указанного типа выражается соотношением:

Природа колебательного вклада в теплоемкость в отличие от поступательного и вращательного значительно сложнее. (см. стр. 18 Пашинкин)

Правило Дюлонга-Пти Согласно этомк правилу атомная теплоемкость простых веществ в твердом состоянии (произведение атомной массы на его удельную теплоемкость) приблизительно одинакова для большинства элементов при комнатной температуре и равна (25,9 – 26,8) Дж/моль К. Однако, правило Дюлонга-Пти строго выполняется для каждого простого вещества лишь при температуре Дебая. C_p ≈ C_v ≈ 26,3 Дж/моль К.

Правило Неймана и Коппа По этому правилу мольная теплоемкость соединений в твердом состоянии приблизительно равна сумме атомных теплоемкостей элементов, входящих в состав данного соединения, если последние не слишком отличаются по своей химической природе.

Интерполяционные уравнения, описывающие температурную зависимость теплоемкости

Экспериментальные значения теплоемкостей индивидуальных веществ при температурах выше 200 К удобно выражать следующими эмпирическими формулами:

С_р = a + bT + cT 2 (5.22)

С_р = a + bT + cT -2 (5.23)

Коэффициенты, входящие в указанные уравнения, различны по значениям. При T = О коэффициент «а» не имеет смысла теплоемкости, а является лишь экстраполяционной постоянной. Уравнение (5.23) лучше передает зависимость С_р от Т при высоких температурах в связи с тем, что вклад третьего члена в общую сумму уменьшается. При этом зависимость С_р от Т становится почти линейной, а при сравнительно низких температурах (сТ -2 ) возрастает, и данная зависимость становится криволинейной, что согласуется с опытными данными. Поэтому небольшая экстраполяция в области высоких и низких температур не связана с большой погрешностью. А небольшая экстраполяция в случае уравнения (5.22 ) может привести к значительным отклонениям, так как при высоких температурах вклад члена сТ 2 в общую теплоемкость большая, что приводит к преувеличенным результатам, или (если С

Видео:Количество теплоты, удельная теплоемкость вещества. Практическая часть - решение задачи. 8 класс.Скачать

Зависимость теплоемкости от температуры

По этой ссылке вы найдёте полный курс лекций по математике:

В практике тепловых расчетов широкое применение получила следующая приближенная зависимость истинной удельной теплоемкости от температуры: где а — экспериментальное значение истинной теплоемкости при температуре О °С; b> d> е — постоянные коэффициенты, зависящие от природы рабочего тела, определяемые на основании экспериментальных данных.

Для менее точных расчетов зависимости истинной удельной теплоемкости от температуры применяется уравнение второй степени: Для двухатомных газов часто ограничиваются первыми двумя членами уравнения (3.13): В табл. 3.1 приведены температурные зависимости истинных мольных теплоемкостей при постоянном давлении для некоторых газов. Зная зависимость с = /(f), можно аналитически определить теплоту или удельную теплоту, исходя из определений «»Я?. Q = JCdt, g-Jcdt. Таблица 3.1 Газ „ х кДж

Мольная теплоемкость С„, ——=т Р кмоль•К Азот 28,97 + 0,002566* Водород 28,78 + 0,001117* Кислород 29,56 + 0,003404* Окись углерода 29,06 + 0,002818* Воздух 29,09 + 0,002412* Водяной пар 32,85 + 0,00544* Углекислота 36,05 + 0,0203* — 0,00000642*2 Однако в практических расчетах используется более простой способ, при котором удельная теплота определяется через среднюю удельную теплоемкость процесса ст: В справочной литературе в основном приводятся коэффициенты для истинной удельной или мольной теплоемкости.

Зная их, можно самостоятельно получить выражение для средних теплоемкостей.

Зависимость истинной удельной теплоемкости от абсолютной температуры с = f(T) можно получить на примере формулы (3.15). Так как t = Т — 273,15, то с = а + b • (Т — 273,15). Обозначив через а’ — а — Ь* 273,15, получим с = а’ + ЬТ. Тогда в процессе нагрева от Тх до Т2 количество сообщенной ТРТ удельной теплоты может быть подсчитано по уравнению д=[а’+|(Г2 + Т1)](Т2-Т1), а средняя удельная теплоемкость запишется в виде Ряд экспериментальных исследований показал, что с понижением температуры теплоемкость водорода быстро уменьшается и уже при Т = 60 К его мольная теплоемкость становится равной теплоемкости идеального одноатомного газа.

Явление падения теплоемкости с понижением

температуры находится в полном соответствии с положениями молекулярно-кинети-ческой теории теплоемкости. При низких абсолютных температурах прекращаются и вращательные движения молекул, и колебательные движения атомов внутри молекул, а остаются лишь три степени свободы поступательного движения, свойственные молекуле идеального одноатомного газа.

Результатом этого и является приближение теплоемкости всех газов при низких температурах к значению теплоемкости идеального одноатомного газа. В 1906 г. Нернст высказал предположение о том, что при последующем понижении температуры и приближении ее к абсолютному нулю должно прекратиться и поступательное движение молекул и тогда любой газ приобретает свойства твердых тел. Проводя опыты над рядом твердых тел вблизи абсолютного нуля, Нернст показал, что теплоемкости твердых тел стремятся к нулю при Т 0 К, а для всех твердых тел при температуре Т — 0 К теплоемкости равны нулю.

Возможно вам будут полезны данные страницы:

Иными словами, при Т = 0 К частицы вещества (молекулы) превращаются в жесткую систему, лишенную тепловых движений. Из этого следует, что эмпирическая зависимость теплоемкости от температуры в виде уравнения (3.18) является справедливой только в области высоких температур и совершенно недействительна в области низких абсолютных температур. Истинный характер изменения теплоемкости от температуры показан на рис. 3.2.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать

Уравнения температурной зависимости теплоемкости вещества

webkonspect.com — сайт, с элементами социальной сети, создан в помощь студентам в их непростой учебной жизни.

Здесь вы сможете создать свой конспект который поможет вам в учёбе.

Чем может быть полезен webkonspect.com:

простота создания и редактирования конспекта (200 вопросов в 3 клика).
просмотр конспекта без выхода в интернет.
удобный текстовый редактор позволит Вам форматировать текст, рисовать таблицы, вставлять математические формулы и фотографии.
конструирование одного конспекта совместно с другом, одногрупником.
webkonspect.com — надёжное место для хранения небольших файлов.