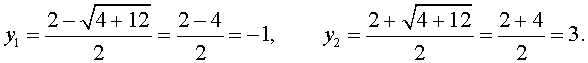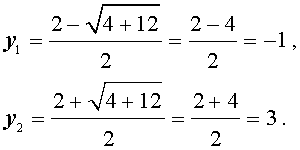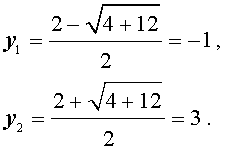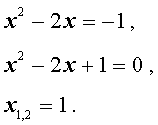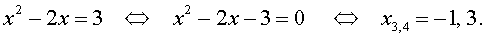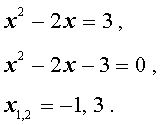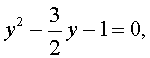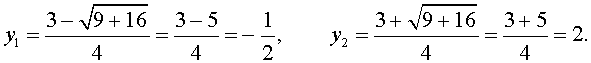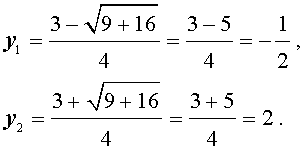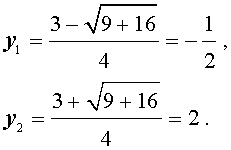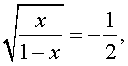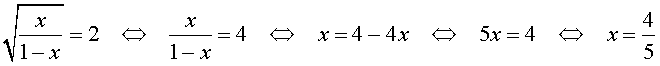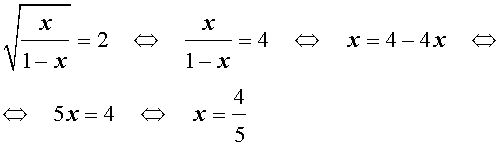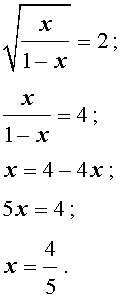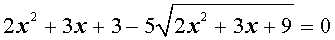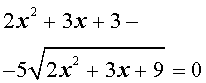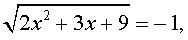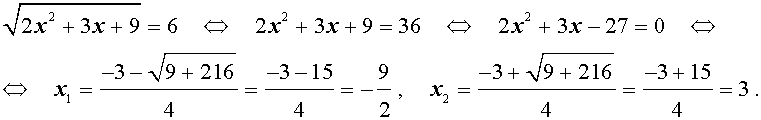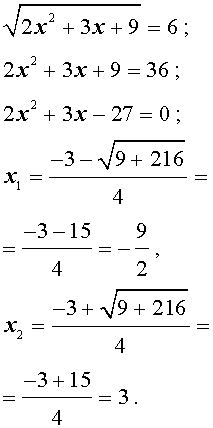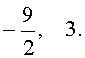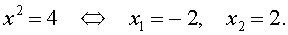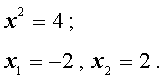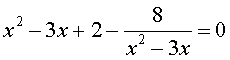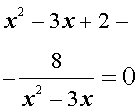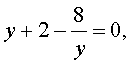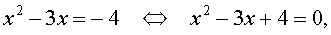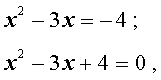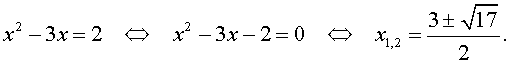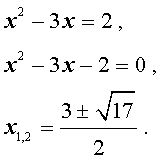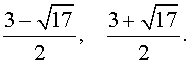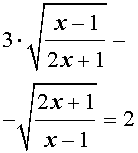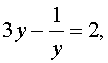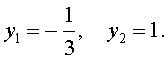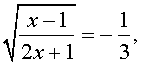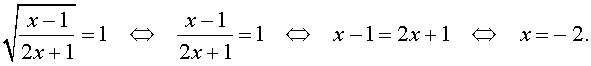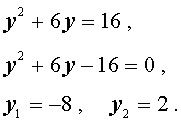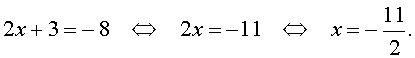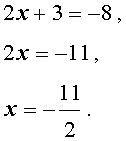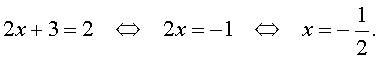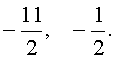трехчленные уравнения и уравнения вида
(ax + b)(ax + b + c)(ax +
+ b + 2c)(ax + b + 3c) = d , левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
 | Трёхчленные уравнения |
 | Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии |
 | Возвратные (симметричные) уравнения 3-ей степени |
 | Возвратные (симметричные) уравнения 4-ой степени |
 | Обобщенные возвратные уравнения 4-ой степени |
Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .
- Трехчленные уравнения
- Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
- Как решать тригонометрические уравнения, сводящиеся к квадратным — примеры
- Основные понятия по теме
- Правила решения тригонометрических уравнений сводящихся к квадратным
- Примеры решения задач с пояснениями
- Решение уравнений, сводящихся к квадратным
- Биквадратные уравнения
- Метод разложения на множители
- Метод замены переменной
- Выделение полного квадрата
- Примеры
- 💥 Видео
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Трехчленные уравнения
Трёхчленными уравнениями называют уравнения вида
| a f 2 (x)+ b f (x) + c = 0, | (1) |
а также уравнения вида
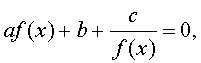 | (2) |
где a, b, c – заданные числа, а f (x) – некоторая функция.
Для того, чтобы решить трехчленное уравнения вида (1), обозначим
| y = f (x), | (3) |
тогда уравнение (1) станет квадратным уравнением относительно переменной y :
| ay 2 + by + c = 0 . | (4) |
Затем найдем корни уравнения (4), а после этого, подставив каждый из найденных корней в равенство (3), решим полученное уравнение относительно x .
Для того, чтобы решить трехчленное уравнение вида (2), сначала введем обозначение (3), а затем умножим полученное уравнение на знаменатель. В результате уравнение (2) примет вид (4), а схема решения уравнения (4) уже описана выше.
Покажем, как это осуществляется на примерах.
Пример 1 . Решить уравнение
| (x 2 – 2x) 2 – – 2(x 2 – 2x) – 3 = 0 . | (5) |
Решение . Если обозначить
| y = x 2 – 2x , | (6) |
то уравнение (5) превратится в квадратное уравнение
| y 2 – 2y – 3 = 0 . | (7) |
В первом случае из равенства (6) получаем:
Во втором случае из равенства (6) получаем:
Пример 2 . Решить уравнение
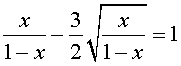 | (8) |
Решение . Если обозначить
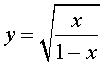 , , | (9) |
то уравнение (8) превратится в квадратное уравнение
которое эквивалентно уравнению
| 2y 2 – 3 y – 2 = 0 . | (10) |
В первом случае из равенства (9) получаем уравнение:
Во втором случае из равенства (9) получаем:
Ответ :
Пример 3 . Решить уравнение
Решение . Если обозначить
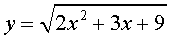 | (12) |
то уравнение (11) превратится в квадратное уравнение
которое эквивалентно уравнению
| y 2 – 5y – 6 = 0 . | (13) |
В первом случае из равенства (12) получаем уравнение:
Во втором случае из равенства (12) получаем:
Ответ :
Пример 4 . Решить биквадратное уравнение
| x 4 – x 2 – 12 = 0 . | (14) |
Решение . Если обозначить
| y = x 2 , | (15) |
то уравнение (14) превратится в квадратное уравнение
| y 2 – y – 12 = 0 . | (16) |
В первом случае из равенства (15) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (15) получаем:
Пример 5 . Решить уравнение
Решение . Если обозначить
| y = x 2 – 3x, | (18) |
уравнение (17) превращается в уравнение
которое при умножении на y принимает вид
| y 2 + 2y – 8 = 0 . | (19) |
В первом случае из равенства (18) получаем квадратное уравнение:
которое решений не имеет.
Во втором случае из равенства (18) получаем:
Ответ :
Пример 6 . Решить уравнение
Решение . Если обозначить
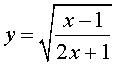 , , | (21) |
уравнение (20) превращается в уравнение
которое при умножении на y принимает вид
| 3y 2 – 2y – 1 = 0 . | (22) |
В первом случае из равенства (21) получаем уравнение
Во втором случае из равенства (21) получаем:
Видео:Решение уравнений сводящихся к квадратным уравнениям. Биквадратные уравнения – 8 класс алгебраСкачать

Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
| (ax + b)(ax + b + + c)(ax + + b + 2c)(ax + + b + 3c) = d , | (23) |
где a, b, c, d – заданные числа, и заметим, что левая часть этого уравнения представляет собой произведение четырёх последовательных членов арифметической прогрессии, первый член которой равен ax+b , а разность равна c .
Схема решения уравнений вида (23) заключается в следующем.
| y = ax + b. | (24) |
Тогда уравнение (23) примет вид:
| y (y + c)(y + + 2c)(y + 3c) = d . | (25) |
Перегруппируем сомножители в левой части уравнения (25) следующим образом:
| [y (y + 3c)][(y + + c)(y + 2c)] = d . | (26) |
Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (26), то получим:
| [y 2 + 3cy][y 2 + + 3cy + 2c 2 ] = d . | (27) |
Если теперь в уравнении (27) обозначить
| z = y 2 + 3cy , | (28) |
то уравнение (27) станеи квадратным уравнением
| z 2 + 2c 2 z – d = 0 . | (29) |
Для того, чтобы найти корни уравнения (23), остаётся решить уравнение (29), затем для каждого корня уравнения (29) решить уравнение (28) относительно y , а затем в каждом из полученных случаев решить уравнение (24) относительно x .
Пример 7 . Решить уравнение
| (2x + 3)(2x + 5)(2x + + 7)(2x + 9) = 384 . | (30) |
Решение .Если обозначить
| y = 2x + 3, | (31) |
уравнение (30) превращается в уравнение
| y (y + 2)(y + + 4)(y + 6) = 384 . | (32) |
Перегруппируем сомножители в левой части уравнения (32):
| [y (y + 6)][(y + + 2)(y + 4)] = 384 . | (33) |
Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (33), то уравнение (33) примет вид:
| [y 2 + 6y][y 2 + + 6y + 8] = 384 . | (34) |
Если теперь обозначить
| z = y 2 + 6y , | (35) |
то уравнение (34) станет квадратным уравнением
| z 2 + 8 z – 384 = 0 . | (36) |
В первом случае из равенства (35) получаем уравнение:
которое корней не имеет.
Во втором случае из равенства (35) получаем:
В первом из этих случаев, из равенства (31) получаем:
Во втором случае из равенства (31) получаем:
Ответ :
Видео:Уравнения, сводящиеся к квадратным. Биквадратное уравнениеСкачать

Как решать тригонометрические уравнения, сводящиеся к квадратным — примеры
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Основные понятия по теме
Тригонометрическими уравнениями называют уравнения с неизвестной, которая расположена строго под знаком тригонометрической функции.
Квадратные тригонометрические уравнения являются такими уравнениями, которые имеют вид:
a sin 2 x + b sin x + c = 0
Здесь a отлично от нуля.
Тригонометрические уравнения, сводящиеся к квадратным, обладают следующими признаками:
- Наличие в уравнении тригонометрических функций от одного аргумента, либо таких, которые можно просто свести к одному аргументу.
- Присутствие в уравнении единственной тригонометрической функции, либо все функции можно свести к одной.
Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Правила решения тригонометрических уравнений сводящихся к квадратным
Рассмотрим случай, когда преобразованное уравнение записано таким образом:
a f 2 ( x ) + b f ( x ) + c = 0
При этом а отлично от нуля, f ( x ) является одной из функций sin x , cos x , tg x , ctg x .
Тогда данное уравнение путем замены f ( x ) = t сводится к квадратному уравнению.
Существует ряд правил, позволяющих решать тригонометрические уравнения, сводящиеся к квадратным. Данная информация будет полезна при выполнении самостоятельных работ и практических заданий в десятом классе.
sin 2 α + cos 2 α = 1 tg α · ctg α = 1 tg α = sin α cos α ctg α = cos α sin α 1 + tg 2 α = 1 cos 2 α 1 + ctg 2 α = 1 sin 2 α ▸
Формулы двойного угла:
sin 2 α = 2 sin α cos α cos 2 α = cos 2 α — sin 2 α sin α cos α = 1 2 sin 2 α cos 2 α = 2 cos 2 α — 1 cos 2 α = 1 — 2 sin 2 α tg 2 α = 2 tg α 1 — tg 2 α ctg 2 α = ctg 2 α — 1 2 ctg α ▸
Последовательность действий при решении тригонометрических уравнений, сводящихся к квадратным:
- выражение одной тригонометрической функции с помощью другой путем применения основных тождеств;
- выполнение подстановки;
- преобразование уравнения;
- введение обозначения, к примеру, sin x = y;
- решение квадратного уравнения;
- обратная замена;
- решение тригонометрического уравнения.
Рассмотрим решение тригонометрического уравнения:
6 cos 2 x — 13 sin x — 13 = 0
cos 2 α = 1 — sin 2 α
В результате уравнение преобразуется таким образом:
6 sin 2 x + 13 sin x + 7 = 0
Заменим sin x на t. Зная, что ОДЗ синуса sin x ∈ [ — 1 ; 1 ] , запишем, t ∈ [ — 1 ; 1 ] . Тогда:
6 t 2 + 13 t + 7 = 0
Заметим, что t 1 не соответствует условиям. Выполним обратную замену и получим решение уравнения:
sin x = — 1 ⇒ x = — π 2 + 2 π n , n ∈ ℤ .
Разберем другой пример:
5 sin 2 x = cos 4 x — 3
Воспользуемся уравнением двойного угла для косинуса:
cos 2 α = 1 — 2 sin 2 α
cos 4 x = 1 — 2 sin 2 2 x
Подставим значения и преобразуем уравнение:
2 sin 2 2 x + 5 sin 2 x + 2 = 0
Заменим sin 2 x на t. Зная, что ОДЗ для синуса sin 2 x ∈ [ — 1 ; 1 ] , можно записать:
2 t 2 + 5 t + 2 = 0
Заметим, что t 1 является посторонним, так как не соответствует условию. Путем обратной замены получим:
sin 2 x = — 1 2 ⇒ x 1 = — π 12 + π n , x 2 = — 5 π 12 + π n , n ∈ ℤ .
Видео:Биквадратные уравнения. 8 класс алгебра.Скачать

Примеры решения задач с пояснениями
Найти корни уравнения:
tg x + 3 ctg x + 4 = 0
При tg x · ctg x = 1 имеем, что:
Заменим tg x на t. Зная, что ОДЗ тангенса tg x ∈ ℝ , запишем:
t + 3 t + 4 = 0 ⇒ t 2 + 4 t + 3 t = 0
Вспомним, что дробь может обладать нулевым значением при нулевом числителе и знаменателе, отличном от нуля. В результате:
Путем обратной замены получим:
Ответ: x = — arctg 3 + π n , x = — π 4 + π n , n ∈ ℤ .
Решить тригонометрическое уравнение на интервале ( — π ; π ) :
2 sin 2 x + 2 sin x — 2 = 0
Заменим sin x на t. В результате уравнение преобразуется:
2 t 2 + 2 t — 2 = 0
Определим дискриминант уравнения:
Таким образом, корни равны:
Исходя из того, что t = sin x ∈ [ — 1 ; 1 ] , можно сделать вывод о лишнем корне t 2 . В результате:
sin x = 2 2 ⇔ x = π 4 + 2 π n
x = 3 π 4 + 2 π m , n , m ∈ ℤ .
Выполним проверку корней на соответствие условиям задания:
— π π 4 + 2 π n π ⇔ — 5 8 n 3 8 ⇒ n = 0 ⇒ x = π 4 .
— π 3 π 4 + 2 π m π ⇔ — 7 8 m 1 8 ⇒ m = 0 ⇒ x = 3 π 4 .
Ответ: корни уравнения π 4 + 2 π n ; 3 π 4 + 2 π m ; n , m ∈ ℤ , из них соответствуют интервалу π 4 ; 3 π 4 .
Дано тригонометрическое уравнение, которое нужно решить на отрезке ( 0 ; π ) :
2 sin 2 x + 2 = 5 sin x
Заметим, что область допустимых значений определяет х как произвольное число. Перенесем члены в левую часть:
2 sin 2 x + 2 — 5 sin x = 0
Данное уравнение является квадратным по отношению к sin x . Заменим sin x на t. Тогда уравнение будет преобразовано таким образом:
2 t 2 — 5 t + 2 = 0
Исходя из того, что sin x ≤ 1 , sin x = 2 является лишним корнем. Таким образом:
Решениями sin x = a являются:
x = arcsin a + 2 π k
x = π — arcsin a + 2 π k
Здесь k ∈ ℤ . В результате, корнями уравнения sin x = 0 , 5 являются:
x = 5 π 6 + 2 π k
Определим, какие корни соответствуют интервалу:
0 π 6 + 2 π k π ⇔ — π 6 2 π k 5 π 6 ⇔ — 1 12 k 5 12
Заметим, что k ∈ ℤ . В таком случае из этих корней подходящими являются лишь те, что соответствуют условию k = 0:
Рассмотрим другие решения:
0 5 π 6 + 2 π k π ⇔ — 5 π 6 2 π k π 6 ⇔ — 5 12 k 1 12
Заметим, что k ∈ ℤ . В таком случае выберем решение при k = 0:
Ответ: корни уравнения π 6 + 2 π k , 5 π 6 + 2 π k , при k ∈ ℤ ; решения, соответствующие интервалу π 6 , 5 π 6 .
Решить уравнение на промежутке [ π ; 3 π ) :
ctg 2 x + 1 cos x — 11 π 2 — 1 = 0
Вспомним формулу приведения:
cos x — 11 π 2 = — sin x
Также пригодится формула:
ctg 2 x + 1 = 1 sin 2 x
1 sin 2 x — 1 — 1 sin x — 1 = 0 ⇔ 1 sin 2 x — 1 sin x — 2 = 0
Заменим 1 sin x на t. В результате:
Путем обратной замены получим:
sin x = — 1 ⇔ x = — π 2 + 2 π n , n ∈ ℤ sin x = 1 2 ⇔ x = π 6 + 2 π k ; x = 5 π 6 + 2 π m , k , m ∈ ℤ .
Определим подходящие решения:
Ответ: корни уравнения — π 2 + 2 π n ; π 6 + 2 π k ; 5 π 6 + 2 π m ; n , k , m ∈ ℤ , из них соответствуют интервалу 3 π 2 ; 13 π 6 ; 17 π 6 .
Определить корни уравнения на отрезке ( π ; 2 π ) :
cos ( 2 x ) + 3 2 sin x = 3
Область допустимых значений предусматривает произвольные значения для х. На первом этапе следует преобразовать уравнение с помощью формулы косинуса двойного угла и перенести члены уравнения в левую сторону:
1 — 2 sin 2 x + 3 2 sin x — 3 = 0 ⇔ 2 sin 2 x — 3 2 sin x + 2 = 0
Заметим, что в результате получено уравнение, которое является квадратным по отношению к sin x . Заменим sin x на t. В результате:
2 t 2 — 3 2 t + 2 = 0
t 1 , 2 = 3 2 ± 2 4
Исходя из того, что sin x ≤ 1 , делаем вывод о лишнем корне sin x = 2 . В результате:
Решения для уравнения sin x = a следующие:
x = arcsin a + 2 π k
x = π — arcsin a + 2 π k
Здесь k ∈ ℤ . В результате получим следующие решения для sin x = 2 2 :
x = 3 π 4 + 2 π k
Определим подходящие корни:
π π 4 + 2 π k 2 π ⇔ 3 π 4 2 π k 7 π 4 ⇔ 3 8 k 7 8
Заметим, что k ∈ ℤ . Тогда указанные корни не соответствуют интервалу ( π ; 2 π ) .
Определим корни, которые подходят к задаче:
π 3 π 4 + 2 π k 2 π ⇔ π 4 2 π k 5 π 4 ⇔ 1 8 k 5 8
Зная, что k ∈ ℤ , можно сделать вывод об отсутствии корней, которые соответствуют интервалу ( π ; 2 π ) .
Ответ: корни уравнения π 4 + 2 π k , 3 π 4 + 2 π k , где k ∈ ℤ , решения, соответствующие интервалу, отсутствуют.
Требуется найти решения тригонометрического уравнения:
3 tg 4 2 x — 10 tg 2 2 x + 3 = 0
Корни нужно записать в соответствии с интервалом — π 4 ; π 4
Область допустимых значений в данном случае:
Заменим tg 2 2 x на t, при t ⩾ 0 . Уравнение будет преобразовано таким образом:
3 t 2 — 10 t + 3 = 0
Путем обратной замены получим:
Можно сделать вывод о выполнении условия относительно области допустимых значений при найденных значениях х . Тогда остается отобрать нужные корни:
— π 4 π 6 + π 2 n 1 π 4 ⇒ — 5 6 n 1 1 6 ⇒ n 1 = 0 ⇒ x = π 6
Вычислим еще три решения, которые включены в заданный интервал:
x = — π 12 ; — π 6 ; π 12 .
Ответ: корнями уравнения являются ± π 6 + π 2 n , ± π 12 + π 2 m , n , m ∈ ℤ , из них соответствуют промежутку — π 6 ; — π 12 ; π 12 ; π 6 .
Видео:Как решать Квадратные уравнения? Урок 15Скачать

Решение уравнений, сводящихся к квадратным
Биквадратные уравнения
Биквадратным уравнением называется уравнение вида:
$$ ax^4+bx^2+c = 0, a neq 0 $$
Алгоритм решения биквадратного уравнения
Шаг 1. Ввести новую переменную: $z = x^2 ge 0$.
Переписать уравнение для новой переменной: $az^2+bz+c = 0$
Шаг 2. Решить полученное квадратное уравнение.
Если $D gt 0$, $z_ = frac<-b pm sqrt> $. Проверить условие $z ≥ 0$, если положительных корней нет, решений нет, переход на шаг 4.
Если D = 0,$z_0 = -frac$. Проверить условие $z ge 0$, если корень отрицательный, решений нет, переход на шаг 4.
Если $D lt 0$, решений нет, переход на шаг 4.
Шаг 3.Если после шага 2 остались положительные корни, найти x: $x = pm sqrt$.
Шаг 4. Работа завершена.
Шаг 1. $z = x^2 ge 0, z^2+7z-30 = 0$
$z_1 = -10 lt 0, z_2 = 3 gt 0 $
Шаг 3. Находим корни из положительного $z: x_ = pm sqrt$
Метод разложения на множители
Решение уравнений, в которые переменная x входит с различными натуральными степенями и вещественными коэффициентами, по существу, является поиском корней многочлена.
Число $x_0$ называют корнем многочлена $P_n (x) = a_n x^n+a_ x^ + ⋯ + a_1 x+a_0$ если $P_n (x_0 ) = 0$.
Для многочлена $P_n$ (x) произвольной степени n справедливо следующее.
Если $x = x_0$ является корнем многочлена $P_n$ (x), то $P_n (x) = (x-x_0) P_ (x)$, где $P_ (x)$ — многочлен степени n-1.
Таким образом, разными способами находя корни и формируя скобки, можно постепенно добиваться понижения степени «оставшегося» многочлена, пока не будут найдены все корни.
При разложении многочлена
- множители вида (x-a) называют линейными множителями ;
- множители вида $ (x^2+bx+c)$, для которых $D lt 0$, называют неприводимыми квадратичными множителями .
Любой многочлен $P_n$ (x) можно представить в виде конечного числа линейных и/или неприводимых квадратичных множителей.
Причём, такое представление единственно с точностью до порядка множителей.
Для разложения многочленов на множители применяются разные методы:
- вынесение общего множителя за скобку (см. §19 справочника для 7 класса);
- группировка (см. §20 справочника для 7 класса);
- формулы сокращенного умножения (см. §25 справочника для 7 класса);
- метод неопределённых коэффициентов;
- выделение полного квадрата и т.п.
Решим уравнение $2x^3-x^2-8x+4 = 0$.
Раскладываем на множители: $x^2 (2x-1)-4(2x-1) = 0$
$$ (x^2-4)(2x-1) = 0 Rightarrow (x-2)(x+2)(2x-1) = 0 $$
Корни уравнения: $x_1 = 2, x_2 = -2, x_3 = frac$
Метод замены переменной
Замена переменной – это уравнение, с помощью которого можно упростить исходное уравнение, и перейти к решению системы из двух более простых уравнений:
$Исходное quad сложное quad уравнение iff <left< begin Новая quad переменная quad (урав. quad связи quad со quad старой quad переменной \ Исходное quad урав. quad в quad «упрощ.» quad виде end right.>$
Например, для биквадратных уравнений:
$$ ax^4+bx^2+c = 0 iff <left< begin z = x^2 ge 0 \ az^2+bz+c = 0 end right.> $$
Можно предложить аналогичные схемы для других уравнений:
$$ ax+b sqrt+c = 0 iff <left< begin z = sqrt ge 0 \ az^2+bz+c = 0 end right.> $$
И, в общем виде, для любой рациональной степени n:
$$ ax^+bx^n+c = 0 iff <left< begin z = x^n \ az^2+bz+c = 0 end right.> , n in Bbb Q $$
В других случаях замена переменной не настолько очевидна.
Но при удачном выборе, этот метод очень упрощает задачу.
Раскроем скобки:$ x^2-x = frac$. Сделаем замену:
$$ z = frac Rightarrow z(z-2) = 24 Rightarrow z^2-2z-24 = 0 Rightarrow (z-6)(z+4) = 0 Rightarrow left[ begin z_1 = -4 \ z_2 = 6 end right.$$
Возвращаемся к исходной переменной x:
$$ left[ begin x^2-x = -4 \ x^2-x = 6 end right. Rightarrow left[ begin x^2-x+4 = 0 \ x^2-x-6 = 0 end right. Rightarrow left[ begin D lt 0, x in varnothing \ (x-3)(x+2) = 0 end right. Rightarrow left[ begin x_1 = -2 \ x_2 = 3 end right. $$
При использовании метода замены переменной не забывайте возвращаться к исходной переменной.
Выделение полного квадрата
Метод выделения полного квадрата является одним из методов разложения на множители. Его идея – представить многочлен в виде разности квадратов двух других многочленов степенью пониже, и разложить разность на две скобки:
$$ P_n (x) = Q_k^2 (x)-R_m^2 (x) = (Q_k (x)-R_m (x))(Q_k (x)+R_m (x)) $$
Такое разложение не всегда возможно.
Рассмотрим выделение полного квадрата для квадратного трёхчлена:
$$ = a Biggl(x+frac Biggr)^2 — frac = a Biggl(x+ frac Biggr)^2- frac, D = b^2-4ac $$
Нами выделен полный квадрат $(x+frac)^2$.
Данное выражение используется для построения и анализа графиков парабол (см. §28 данного справочника).
А его разложение на две линейные скобки, известное как теорема Виета (см. §26 данного справочника), возможно только при условии $D ge 0$.
Решить уравнение $x^4+4x^2-1 = 0$
Выделим полный квадрат и разложим на множители:
$$ left[ begin x^2+2-sqrt = 0 \ x^2+2+sqrt = 0 end right. Rightarrow left[ begin x^2 = sqrt -2 gt 0 \ x^2 = -(2+sqrt) lt 0 end right. Rightarrow x_1,2 = pm sqrt<sqrt-2> $$
Примеры
Пример 1. Решите биквадратные уравнения:
Делаем замену: $2x^4+7x^2-4 = 0 iff <left< begin z = x^2 ge 0 \ 2z^2+7z-4 = 0 end right.>$
Решаем квадратное уравнение: $D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2$
$$ z = frac = left[ begin z_1 = -4 lt 0 \ z_2 = frac gt 0 end right. $$
Выбираем положительный z и возвращаемся к исходной переменной x:
Делаем замену: $(x+3)^4-10(x+3)^2+24 = 0 iff <left< begin z = (x+3)^2 ge 0 \ z^2-10z+24 = 0 end right.>$
Решаем квадратное уравнение: $z^2-10z+24 = 0 Rightarrow (z-4)(z-6) = 0 Rightarrow left[ begin z_1 = 4 \ z_2 = 6 end right.$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin (x+3)^2 = 4 \ (x+3)^2 = 6 end right. Rightarrow left[ begin x+3 = pm sqrt \ x+3 = pm sqrt end right. Rightarrow left[ begin x_ = -3 pm 2 \ x_ = -3 pm sqrt end right. Rightarrow left[ begin x_1 = -5 \ x_2 = -1 \ x_ = -3 pm sqrt end right. $$
Пример 2. Решите уравнения аналогичные биквадратным:
Делаем замену: $x+4 sqrt-60 = 0 iff <left< begin z = sqrt ge 0 \ z^2+4z-60 = 0 end right.>$
Решаем квадратное уравнение: $ z^2+4z-60 = 0 Rightarrow (z+10)(z-6) = 0 Rightarrow left[ begin z_1 = -10 \ z_2 = 6 end right.$
Выбираем положительный корень и возвращаемся к исходной переменной:
Делаем замену: $(x-1)^6-7(x-1)^3-8 = 0 iff <left< begin z = (x-1)^3 \ z^2-7z-8 = 0 end right.>$
Решаем квадратное уравнение: $ z^2-7z-8 = 0 Rightarrow (z+1)(z-8) = 0 Rightarrow left[ begin z_1 = -1 \ z_2 = 8 end right.$
При замене куба знак z может быть любым, берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin (x-1)^3 = -1 \ (x-1)^3 = 8 end right. Rightarrow left[ begin x-1 = -1 \ x-1 = 2 end right. Rightarrow left[ begin x_1 = 0 \ x_2 = 3 end right. $$
Пример 3. Решите уравнения с помощью замены переменной:
Заметим, что $(x+3)^2 = x^2+6x+9$. Получаем:
$$ (x^2+6x)^2-(x^2+6x+9) = 33 Rightarrow (x^2+6x)^2-(x^2+6x)-42 = 0 $$
Решаем квадратное уравнение: $ z^2-z-42 = 0 Rightarrow (z+6)(z-7) = 0 Rightarrow left[ begin z_1 = -6 \ z_2 = 7 end right.$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin x^2+6x = -6 \ x^2+6x = 7 end right. Rightarrow left[ begin x^2+6x+6 = 0 \ x^2+6x-7=0 end right. Rightarrow left[ begin D = 12, x = frac<-6 pm 2 sqrt> \ (x+7)(x-1) = 0 end right. Rightarrow left[ begin x_ = -3 pm sqrt \ x_3 = -7 \ x_4 = 1 end right. $$
Делаем замену: $ frac + frac = 2 iff left[ begin z = x^2+3 ge 3 \ frac + frac = 2 end right.$
Решаем уравнение относительно z:
$$ frac + frac = 2 Rightarrow frac = frac Rightarrow 4(z+1)+5z = 2z(z+1) $$
$$ 2z^2+2z-9z-4 = 0 Rightarrow 2z^2-7z-4 = 0 $$
$$ D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2 $$
$$ z = frac = left[ begin z_1 = — frac lt 3 \ z_2 = 4 gt 3 end right. $$
Выбираем корень больше 3 и возвращаемся к исходной переменной:
$$ x^2+3 = 4 Rightarrow x^2 = 1 Rightarrow x_ = pm 1$$
Пример 4*. Решите уравнения:
Приведём это уравнение к биквадратному.
В линейных множителях (x+a) выберем все a =
Найдем их среднее арифметическое (см. §52 справочника для 7 класса)
Замена переменных $z = x+a_$:
Упрощаем уравнение, используя формулу разности квадратов:
$$ (z^2-9)(z^2-1) = 945 Rightarrow z^4-10z^2+9 = 945 Rightarrow z^4-10z^2-936 = 0 $$
Получили биквадратное уравнение.
Делаем замену: $z^4-10z^2-936 = 0 iff <left< begin t = z^2 ge 0 \ t^2-10t-936 = 0 end right.> $
Решаем квадратное уравнение:
$$ D = 100+4 cdot 936 = 3844 = 62^2, t = frac = left[ begin t_1 = -26 lt 0 \ t_2 = 36 gt 0 end right. $$
Выбираем положительный корень и возвращаемся к переменной z:
$$ z = pm sqrt = pm sqrt = pm 6 $$
Возвращаемся к исходной переменной x:
$$ x = z-4 = pm 6-4 = left[ begin x_1 = -10 \ x_2 = 2 end right. $$
$$ z- frac =2,1 |times z (z neq 0) $$
$$ z^2-2,1z-1 = 0 Rightarrow D = 2,1^2+4 = 8,41 = 2,9^2; z = frac = left[ begin z_1 = -0,4 \ z_2 = 2,5 end right. $$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin frac = -0,4 \ frac = 2,5 end right. Rightarrow left[ begin x^2+1 = -0,4x \x^2+1 = 2,5x end right. Rightarrow left[ begin x^2+0,4x+1 = 0 \ x^2-2,5x+1 = 0 end right. $$
В первом уравнении $D = 0,4^2-4 lt 0$, решений нет.
Во втором уравнении (x-2)(x-1/2) = 0 $Rightarrow left[ begin x_1 = frac \ x_2 = 2 end right.$
💥 Видео
Неполные квадратные уравнения. Алгебра, 8 классСкачать

Ты не решишь тригонометрию на ДВИ без этой формулы! 😎Скачать

АЛГЕБРА 8 класс : Решение неполных квадратных уравнений | ВидеоурокСкачать

МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?Скачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Теорема Виета. 8 класс.Скачать

Алгебра 8 класс (Урок№27 - Квадратные уравнения. Неполные квадратные уравнения.)Скачать

Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Алгебра 8. Решение уравнений, сводящихся к квадратнымСкачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Уравнения, сводящиеся к квадратным | Квадратный трёхчлен #4 | Ботай со мной #023 | Борис ТрушинСкачать

Как решать уравнения с дробью? #shortsСкачать