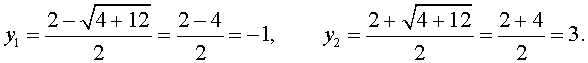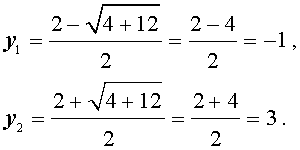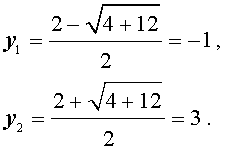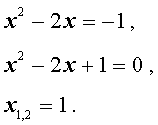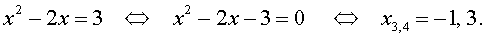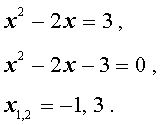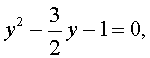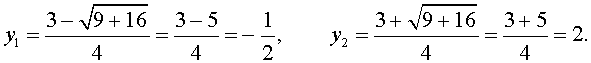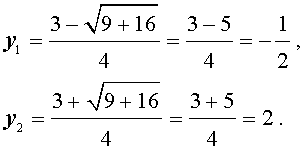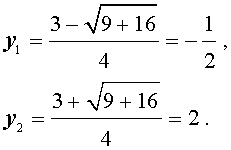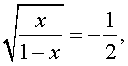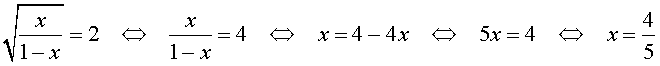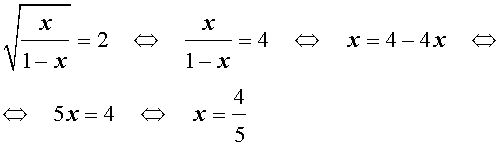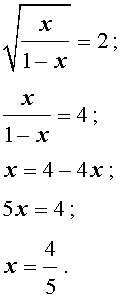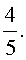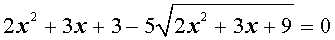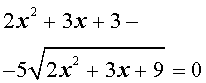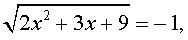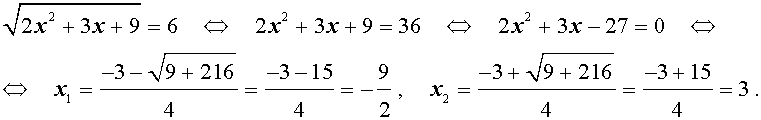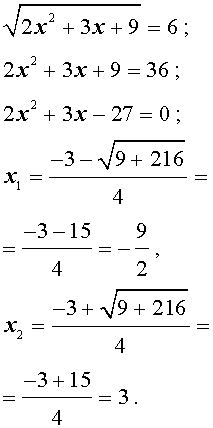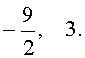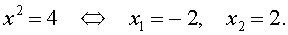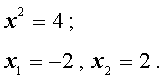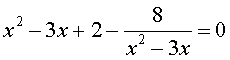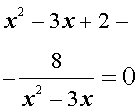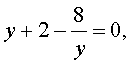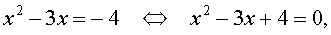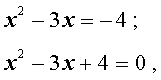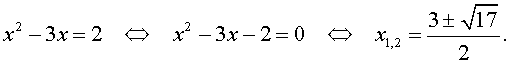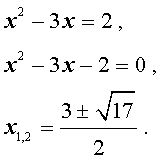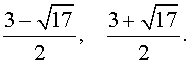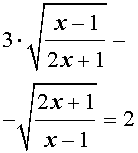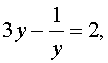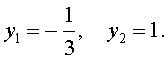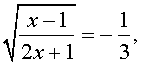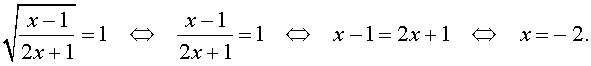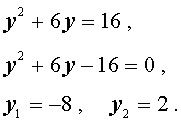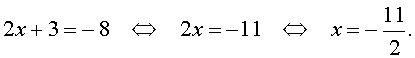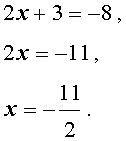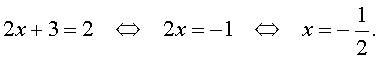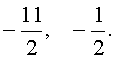трехчленные уравнения и уравнения вида
(ax + b)(ax + b + c)(ax +
+ b + 2c)(ax + b + 3c) = d , левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
 | Трёхчленные уравнения |
 | Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии |
 | Возвратные (симметричные) уравнения 3-ей степени |
 | Возвратные (симметричные) уравнения 4-ой степени |
 | Обобщенные возвратные уравнения 4-ой степени |
Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .
- Трехчленные уравнения
- Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
- Как решать тригонометрические уравнения, сводящиеся к квадратным — примеры
- Основные понятия по теме
- Правила решения тригонометрических уравнений сводящихся к квадратным
- Примеры решения задач с пояснениями
- Конспект урока по теме «Уравнения, сводящиеся к квадратным»
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 🎬 Видео
Видео:Тригонометрические уравнения, сводящиеся к квадратным. 10 классСкачать

Трехчленные уравнения
Трёхчленными уравнениями называют уравнения вида
| a f 2 (x)+ b f (x) + c = 0, | (1) |
а также уравнения вида
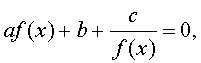 | (2) |
где a, b, c – заданные числа, а f (x) – некоторая функция.
Для того, чтобы решить трехчленное уравнения вида (1), обозначим
| y = f (x), | (3) |
тогда уравнение (1) станет квадратным уравнением относительно переменной y :
| ay 2 + by + c = 0 . | (4) |
Затем найдем корни уравнения (4), а после этого, подставив каждый из найденных корней в равенство (3), решим полученное уравнение относительно x .
Для того, чтобы решить трехчленное уравнение вида (2), сначала введем обозначение (3), а затем умножим полученное уравнение на знаменатель. В результате уравнение (2) примет вид (4), а схема решения уравнения (4) уже описана выше.
Покажем, как это осуществляется на примерах.
Пример 1 . Решить уравнение
| (x 2 – 2x) 2 – – 2(x 2 – 2x) – 3 = 0 . | (5) |
Решение . Если обозначить
| y = x 2 – 2x , | (6) |
то уравнение (5) превратится в квадратное уравнение
| y 2 – 2y – 3 = 0 . | (7) |
В первом случае из равенства (6) получаем:
Во втором случае из равенства (6) получаем:
Пример 2 . Решить уравнение
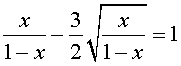 | (8) |
Решение . Если обозначить
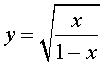 , , | (9) |
то уравнение (8) превратится в квадратное уравнение
которое эквивалентно уравнению
| 2y 2 – 3 y – 2 = 0 . | (10) |
В первом случае из равенства (9) получаем уравнение:
Во втором случае из равенства (9) получаем:
Ответ :
Пример 3 . Решить уравнение
Решение . Если обозначить
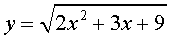 | (12) |
то уравнение (11) превратится в квадратное уравнение
которое эквивалентно уравнению
| y 2 – 5y – 6 = 0 . | (13) |
В первом случае из равенства (12) получаем уравнение:
Во втором случае из равенства (12) получаем:
Ответ :
Пример 4 . Решить биквадратное уравнение
| x 4 – x 2 – 12 = 0 . | (14) |
Решение . Если обозначить
| y = x 2 , | (15) |
то уравнение (14) превратится в квадратное уравнение
| y 2 – y – 12 = 0 . | (16) |
В первом случае из равенства (15) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (15) получаем:
Пример 5 . Решить уравнение
Решение . Если обозначить
| y = x 2 – 3x, | (18) |
уравнение (17) превращается в уравнение
которое при умножении на y принимает вид
| y 2 + 2y – 8 = 0 . | (19) |
В первом случае из равенства (18) получаем квадратное уравнение:
которое решений не имеет.
Во втором случае из равенства (18) получаем:
Ответ :
Пример 6 . Решить уравнение
Решение . Если обозначить
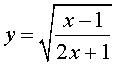 , , | (21) |
уравнение (20) превращается в уравнение
которое при умножении на y принимает вид
| 3y 2 – 2y – 1 = 0 . | (22) |
В первом случае из равенства (21) получаем уравнение
Во втором случае из равенства (21) получаем:
Видео:Алгебра 10 класс Уравнения,сводящиеся к квадратнымСкачать

Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
| (ax + b)(ax + b + + c)(ax + + b + 2c)(ax + + b + 3c) = d , | (23) |
где a, b, c, d – заданные числа, и заметим, что левая часть этого уравнения представляет собой произведение четырёх последовательных членов арифметической прогрессии, первый член которой равен ax+b , а разность равна c .
Схема решения уравнений вида (23) заключается в следующем.
| y = ax + b. | (24) |
Тогда уравнение (23) примет вид:
| y (y + c)(y + + 2c)(y + 3c) = d . | (25) |
Перегруппируем сомножители в левой части уравнения (25) следующим образом:
| [y (y + 3c)][(y + + c)(y + 2c)] = d . | (26) |
Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (26), то получим:
| [y 2 + 3cy][y 2 + + 3cy + 2c 2 ] = d . | (27) |
Если теперь в уравнении (27) обозначить
| z = y 2 + 3cy , | (28) |
то уравнение (27) станеи квадратным уравнением
| z 2 + 2c 2 z – d = 0 . | (29) |
Для того, чтобы найти корни уравнения (23), остаётся решить уравнение (29), затем для каждого корня уравнения (29) решить уравнение (28) относительно y , а затем в каждом из полученных случаев решить уравнение (24) относительно x .
Пример 7 . Решить уравнение
| (2x + 3)(2x + 5)(2x + + 7)(2x + 9) = 384 . | (30) |
Решение .Если обозначить
| y = 2x + 3, | (31) |
уравнение (30) превращается в уравнение
| y (y + 2)(y + + 4)(y + 6) = 384 . | (32) |
Перегруппируем сомножители в левой части уравнения (32):
| [y (y + 6)][(y + + 2)(y + 4)] = 384 . | (33) |
Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (33), то уравнение (33) примет вид:
| [y 2 + 6y][y 2 + + 6y + 8] = 384 . | (34) |
Если теперь обозначить
| z = y 2 + 6y , | (35) |
то уравнение (34) станет квадратным уравнением
| z 2 + 8 z – 384 = 0 . | (36) |
В первом случае из равенства (35) получаем уравнение:
которое корней не имеет.
Во втором случае из равенства (35) получаем:
В первом из этих случаев, из равенства (31) получаем:
Во втором случае из равенства (31) получаем:
Ответ :
Видео:Уравнения, сводящиеся к квадратным. Видеоурок 31. Алгебра 10 классСкачать

Как решать тригонометрические уравнения, сводящиеся к квадратным — примеры
Видео:Решение уравнений сводящихся к квадратным уравнениям. Биквадратные уравнения – 8 класс алгебраСкачать

Основные понятия по теме
Тригонометрическими уравнениями называют уравнения с неизвестной, которая расположена строго под знаком тригонометрической функции.
Квадратные тригонометрические уравнения являются такими уравнениями, которые имеют вид:
a sin 2 x + b sin x + c = 0
Здесь a отлично от нуля.
Тригонометрические уравнения, сводящиеся к квадратным, обладают следующими признаками:
- Наличие в уравнении тригонометрических функций от одного аргумента, либо таких, которые можно просто свести к одному аргументу.
- Присутствие в уравнении единственной тригонометрической функции, либо все функции можно свести к одной.
Видео:Тригонометрические уравнения, приводимые к квадратным | Алгебра 10 классСкачать

Правила решения тригонометрических уравнений сводящихся к квадратным
Рассмотрим случай, когда преобразованное уравнение записано таким образом:
a f 2 ( x ) + b f ( x ) + c = 0
При этом а отлично от нуля, f ( x ) является одной из функций sin x , cos x , tg x , ctg x .
Тогда данное уравнение путем замены f ( x ) = t сводится к квадратному уравнению.
Существует ряд правил, позволяющих решать тригонометрические уравнения, сводящиеся к квадратным. Данная информация будет полезна при выполнении самостоятельных работ и практических заданий в десятом классе.
sin 2 α + cos 2 α = 1 tg α · ctg α = 1 tg α = sin α cos α ctg α = cos α sin α 1 + tg 2 α = 1 cos 2 α 1 + ctg 2 α = 1 sin 2 α ▸
Формулы двойного угла:
sin 2 α = 2 sin α cos α cos 2 α = cos 2 α — sin 2 α sin α cos α = 1 2 sin 2 α cos 2 α = 2 cos 2 α — 1 cos 2 α = 1 — 2 sin 2 α tg 2 α = 2 tg α 1 — tg 2 α ctg 2 α = ctg 2 α — 1 2 ctg α ▸
Последовательность действий при решении тригонометрических уравнений, сводящихся к квадратным:
- выражение одной тригонометрической функции с помощью другой путем применения основных тождеств;
- выполнение подстановки;
- преобразование уравнения;
- введение обозначения, к примеру, sin x = y;
- решение квадратного уравнения;
- обратная замена;
- решение тригонометрического уравнения.
Рассмотрим решение тригонометрического уравнения:
6 cos 2 x — 13 sin x — 13 = 0
cos 2 α = 1 — sin 2 α
В результате уравнение преобразуется таким образом:
6 sin 2 x + 13 sin x + 7 = 0
Заменим sin x на t. Зная, что ОДЗ синуса sin x ∈ [ — 1 ; 1 ] , запишем, t ∈ [ — 1 ; 1 ] . Тогда:
6 t 2 + 13 t + 7 = 0
Заметим, что t 1 не соответствует условиям. Выполним обратную замену и получим решение уравнения:
sin x = — 1 ⇒ x = — π 2 + 2 π n , n ∈ ℤ .
Разберем другой пример:
5 sin 2 x = cos 4 x — 3
Воспользуемся уравнением двойного угла для косинуса:
cos 2 α = 1 — 2 sin 2 α
cos 4 x = 1 — 2 sin 2 2 x
Подставим значения и преобразуем уравнение:
2 sin 2 2 x + 5 sin 2 x + 2 = 0
Заменим sin 2 x на t. Зная, что ОДЗ для синуса sin 2 x ∈ [ — 1 ; 1 ] , можно записать:
2 t 2 + 5 t + 2 = 0
Заметим, что t 1 является посторонним, так как не соответствует условию. Путем обратной замены получим:
sin 2 x = — 1 2 ⇒ x 1 = — π 12 + π n , x 2 = — 5 π 12 + π n , n ∈ ℤ .
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Примеры решения задач с пояснениями
Найти корни уравнения:
tg x + 3 ctg x + 4 = 0
При tg x · ctg x = 1 имеем, что:
Заменим tg x на t. Зная, что ОДЗ тангенса tg x ∈ ℝ , запишем:
t + 3 t + 4 = 0 ⇒ t 2 + 4 t + 3 t = 0
Вспомним, что дробь может обладать нулевым значением при нулевом числителе и знаменателе, отличном от нуля. В результате:
Путем обратной замены получим:
Ответ: x = — arctg 3 + π n , x = — π 4 + π n , n ∈ ℤ .
Решить тригонометрическое уравнение на интервале ( — π ; π ) :
2 sin 2 x + 2 sin x — 2 = 0
Заменим sin x на t. В результате уравнение преобразуется:
2 t 2 + 2 t — 2 = 0
Определим дискриминант уравнения:
Таким образом, корни равны:
Исходя из того, что t = sin x ∈ [ — 1 ; 1 ] , можно сделать вывод о лишнем корне t 2 . В результате:
sin x = 2 2 ⇔ x = π 4 + 2 π n
x = 3 π 4 + 2 π m , n , m ∈ ℤ .
Выполним проверку корней на соответствие условиям задания:
— π π 4 + 2 π n π ⇔ — 5 8 n 3 8 ⇒ n = 0 ⇒ x = π 4 .
— π 3 π 4 + 2 π m π ⇔ — 7 8 m 1 8 ⇒ m = 0 ⇒ x = 3 π 4 .
Ответ: корни уравнения π 4 + 2 π n ; 3 π 4 + 2 π m ; n , m ∈ ℤ , из них соответствуют интервалу π 4 ; 3 π 4 .
Дано тригонометрическое уравнение, которое нужно решить на отрезке ( 0 ; π ) :
2 sin 2 x + 2 = 5 sin x
Заметим, что область допустимых значений определяет х как произвольное число. Перенесем члены в левую часть:
2 sin 2 x + 2 — 5 sin x = 0
Данное уравнение является квадратным по отношению к sin x . Заменим sin x на t. Тогда уравнение будет преобразовано таким образом:
2 t 2 — 5 t + 2 = 0
Исходя из того, что sin x ≤ 1 , sin x = 2 является лишним корнем. Таким образом:
Решениями sin x = a являются:
x = arcsin a + 2 π k
x = π — arcsin a + 2 π k
Здесь k ∈ ℤ . В результате, корнями уравнения sin x = 0 , 5 являются:
x = 5 π 6 + 2 π k
Определим, какие корни соответствуют интервалу:
0 π 6 + 2 π k π ⇔ — π 6 2 π k 5 π 6 ⇔ — 1 12 k 5 12
Заметим, что k ∈ ℤ . В таком случае из этих корней подходящими являются лишь те, что соответствуют условию k = 0:
Рассмотрим другие решения:
0 5 π 6 + 2 π k π ⇔ — 5 π 6 2 π k π 6 ⇔ — 5 12 k 1 12
Заметим, что k ∈ ℤ . В таком случае выберем решение при k = 0:
Ответ: корни уравнения π 6 + 2 π k , 5 π 6 + 2 π k , при k ∈ ℤ ; решения, соответствующие интервалу π 6 , 5 π 6 .
Решить уравнение на промежутке [ π ; 3 π ) :
ctg 2 x + 1 cos x — 11 π 2 — 1 = 0
Вспомним формулу приведения:
cos x — 11 π 2 = — sin x
Также пригодится формула:
ctg 2 x + 1 = 1 sin 2 x
1 sin 2 x — 1 — 1 sin x — 1 = 0 ⇔ 1 sin 2 x — 1 sin x — 2 = 0
Заменим 1 sin x на t. В результате:
Путем обратной замены получим:
sin x = — 1 ⇔ x = — π 2 + 2 π n , n ∈ ℤ sin x = 1 2 ⇔ x = π 6 + 2 π k ; x = 5 π 6 + 2 π m , k , m ∈ ℤ .
Определим подходящие решения:
Ответ: корни уравнения — π 2 + 2 π n ; π 6 + 2 π k ; 5 π 6 + 2 π m ; n , k , m ∈ ℤ , из них соответствуют интервалу 3 π 2 ; 13 π 6 ; 17 π 6 .
Определить корни уравнения на отрезке ( π ; 2 π ) :
cos ( 2 x ) + 3 2 sin x = 3
Область допустимых значений предусматривает произвольные значения для х. На первом этапе следует преобразовать уравнение с помощью формулы косинуса двойного угла и перенести члены уравнения в левую сторону:
1 — 2 sin 2 x + 3 2 sin x — 3 = 0 ⇔ 2 sin 2 x — 3 2 sin x + 2 = 0
Заметим, что в результате получено уравнение, которое является квадратным по отношению к sin x . Заменим sin x на t. В результате:
2 t 2 — 3 2 t + 2 = 0
t 1 , 2 = 3 2 ± 2 4
Исходя из того, что sin x ≤ 1 , делаем вывод о лишнем корне sin x = 2 . В результате:
Решения для уравнения sin x = a следующие:
x = arcsin a + 2 π k
x = π — arcsin a + 2 π k
Здесь k ∈ ℤ . В результате получим следующие решения для sin x = 2 2 :
x = 3 π 4 + 2 π k
Определим подходящие корни:
π π 4 + 2 π k 2 π ⇔ 3 π 4 2 π k 7 π 4 ⇔ 3 8 k 7 8
Заметим, что k ∈ ℤ . Тогда указанные корни не соответствуют интервалу ( π ; 2 π ) .
Определим корни, которые подходят к задаче:
π 3 π 4 + 2 π k 2 π ⇔ π 4 2 π k 5 π 4 ⇔ 1 8 k 5 8
Зная, что k ∈ ℤ , можно сделать вывод об отсутствии корней, которые соответствуют интервалу ( π ; 2 π ) .
Ответ: корни уравнения π 4 + 2 π k , 3 π 4 + 2 π k , где k ∈ ℤ , решения, соответствующие интервалу, отсутствуют.
Требуется найти решения тригонометрического уравнения:
3 tg 4 2 x — 10 tg 2 2 x + 3 = 0
Корни нужно записать в соответствии с интервалом — π 4 ; π 4
Область допустимых значений в данном случае:
Заменим tg 2 2 x на t, при t ⩾ 0 . Уравнение будет преобразовано таким образом:
3 t 2 — 10 t + 3 = 0
Путем обратной замены получим:
Можно сделать вывод о выполнении условия относительно области допустимых значений при найденных значениях х . Тогда остается отобрать нужные корни:
— π 4 π 6 + π 2 n 1 π 4 ⇒ — 5 6 n 1 1 6 ⇒ n 1 = 0 ⇒ x = π 6
Вычислим еще три решения, которые включены в заданный интервал:
x = — π 12 ; — π 6 ; π 12 .
Ответ: корнями уравнения являются ± π 6 + π 2 n , ± π 12 + π 2 m , n , m ∈ ℤ , из них соответствуют промежутку — π 6 ; — π 12 ; π 12 ; π 6 .
Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Конспект урока по теме «Уравнения, сводящиеся к квадратным»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
муниципальное автономное общеобразовательное учреждение
«Свободненская средняя общеобразовательная школа»
« Уравнения, сводящиеся к квадратным »
(Алгебра 8 класс)
Алеевская Татьяна Петровна
Тема урока: « Уравнения, сводящиеся к квадратным »
Класс: 8 класс, учебник «Алгебра – 8» Ш.А. Алимов и др. Форма проведения: урок изучения и первичного закрепления новых знаний.
Систематизация знаний, учащихся по теме «Квадратные уравнения» и «Уравнения, сводящиеся к квадратным». Изучение алгоритма решения уравнений, сводящимся к квадратным методом замены переменных, решение уравнений из второй части ОГЭ.
Воспитание дисциплинированности, самостоятельности, упорства в достижении поставленной цели, формирование интеллектуальные умений.
Развитие навыков памяти, самоконтроля, наблюдательности, умения правильно обобщать и делать вывод. культуру устной и письменной речи.
Тип урока : урок изучения новой темы.
Место проведения : учебный кабинет
Оборудование : Учебник: Алгебра, 8 класс. Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин, Издательство «Просвещение», 2019 г. Карточки, школьная доска-компьютер, доска для маркера.
Формирование навыков решения уравнений, сводящихся к квадратным, навыков исследовательской работы, работы в парах и индивидуально, привитие интереса к предмету, навыков самооценки.
2. Проверка домашнего задания.
3. Актуализация знаний и умений.
- Первичное усвоения новых знаний.
- Работа в парах, направленная на первичное закрепление новых знаний.
- Физкультминутка.
- Решение более сложных заданий.
- Задание на дом.
- Итог урока. Выставление оценок учащимся.
1. Организационный момент:
Организация начала занятия, приветствие, проверка готовности класса к уроку.
2. Проверка домашнего задания
3 ученика вызываются к доске с заданиями: разложить квадратный трёхчлен на множители. Задания аналогичные домашней работе. Один ученик находит корни квадратного трёхчлена по приведенному уравнению, другой – по полному, третий решает, как удобнее.
Разложите на множители:
Разложите на множители:
Разложите на множители:1) x 2 -8 x — 9
3. Актуализация знаний и умений .
Работа по закреплению знаний, полученных на прошлом уроке.
Фронтальная работа с классом . Повторение теоретического материала по изученной теме «Квадратные уравнения».
Что такое уравнение? Что такое корень уравнения? Что значит решить уравнение?
Какие уравнения мы называем линейными? Какие уравнения мы называем квадратными? Приведите примеры.
Сколько корней может иметь линейное уравнение (квадратное) уравнение?
Какие виды неполных квадратных уравнений вам известны? Приведите примеры.
Какой общий вид имеет полное квадратное уравнение? Приведите пример.
Какие квадратные уравнения мы умеем решать? Приведите примеры.
Назовите корни следующих квадратных уравнений. Как называется этот вид уравнений?
Почему последнее уравнение не имеет корней?
1. Первичное усвоения новых знаний
Мы научились решать квадратные уравнения по формулам. Как полного квадратного уравнения, так и приведенного. Мы умеем решать такие уравнения и по теореме, обратной теореме Виета.
Ученик у доски. Решает квадратное уравнение:
1) x 2 -10x + 9 = 0
x 1 
Теперь подумаем, как решить вот такое уравнение:
2) x 4 -10 x 2 + 9 = 0,
Какая степень уравнения? Как можно понизить степень данного уравнения? Вводим замену переменной: x 2 = t . Получим уравнение: t 2 -10 t + 9 = 0. Чем оно отличается от первого уравнения? Мы уже вычислили корни данного уравнения. Теперь вернёмся к нашей замене переменной и решим получившиеся неполные квадратные уравнения:
Сколько корней получили в ответе?
3) Решим следующее уравнение. Второй ученик у доски.
x 4 -3 x 2 — 4 = 0. Введите замену переменной x 2 = t .
t1 
Вернёмся к замене переменной.
Имеет ли корни уравнение x 2 = -1? Сколько действительных корней будет иметь данное уравнение?
Класс решает уравнения по учебнику № 468(2), №469(2) . Одновременно два ученика на доске решают следующие уравнения.
Уравнения учеников: x 4 -6 x 2 — 5 = 0; x 4 — 2 x 2 — 3 = 0.
Затем проверяются уравнения, решенные учениками на доске, и идет переход на другую страницу доски-компьютера, на которой решение уже написано.
1) Закрыть глаза, сильно напрягая глазные мышцы, на счет 1 -4, затем раскрыть глаза, расслабив мышцы глаз, посмотреть вдаль на счет 1-5. Повторить 4-5 раз.
2) Посмотреть на переносицу и задержать взор на счет 1-4. До усталости глаза не доводить. Затем открыть глаза, посмотреть вдаль на счет 1-5. Повторить 4-5 раз.
3) Нарисовать глазами восьмёрку.
4) Потереть руками пальцы, похлопать в ладоши. (Устают не только глаза, но и пальцы, держащие ручку).
7. Решение более сложных заданий.
(Задания №19 второй части ОГЭ)
Продолжаем освоение нового метода решения уравнений. Предлагаю решить следующие уравнения:
Как можно освободиться от дроби? Какая замена переменной нас устроит?
t1 
Вернёмся к замене переменной.
Каждое из получившихся приведённых уравнений имеет корни? Почему первое уравнение не имеет решения?
Ответ: — 


x 2 =
Найдем корни следующего уравнения:





1= — x +3 4( x — 3) = 1
x = 2 x -3 =
x = 3 

Ребята, вы поняли метод решения данного типа уравнений? Уравнения для закрепления темы решаем в парах с последующей проверкой на доске.
1) ( x — 3) 4 – 5( x — 3) 2 – 14 = 0
Одновременно два ученика решают у доски похожие уравнения:
№1. ( x + 2) 4 – 3( x + 2) 2 – 18 = 0
№2.
8. Домашнее задание: № 468(3), №469(3) , 472.
9. Итог урока. Выставление оценок учащимся.
Какой тип уравнений мы научились решать? Сколько корней может иметь квадратное уравнение? Сколько корней может иметь уравнение четвертой степени? От чего это зависит? С какой целью мы вводили замену переменных? (В первом случае понизили степень уравнения, во втором случае не стали приводить к общему знаменателю алгебраические дроби, чем и упростили решениеуравнений).
На уроке я разобрался в теме и успел сделать…
В результате научился…
Я не понял, у меня не получилось…
Кому на уроке все было понятно встаньте и похлопайте в ладоши, у крого остались вопросы и не все получалось поднимите руки.
Краткое описание документа:
Сначала решается приведенное квадратное уравнение. Затем предлагается решить уравнение четвертой степени, причем, после замены переменной мы приходим к предыдущему уравнению, еще и еще раз предлагается решить более сложные уравнения. В результате приходим к предыдущему уравнению. После этого обсуждаем принцип решения подобных уранений и закрепляем полученные знания самостоятельной работой. Такой подход экономит время на уроке и позволяет больше решить приведенных уравнений.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 945 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 687 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 315 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 591 090 материалов в базе
Материал подходит для УМК
«Алгебра», Алимов Ш.А. и др.
§ 30. Уравнения, сводящиеся к квадратным
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 10.02.2022
- 168
- 9
- 10.02.2022
- 50
- 1
- 10.02.2022
- 24
- 0
- 10.02.2022
- 30
- 0
- 10.02.2022
- 27
- 0
- 10.02.2022
- 42
- 2
- 10.02.2022
- 31
- 0
- 10.02.2022
- 59
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 10.02.2022 96
- DOCX 107 кбайт
- 1 скачивание
- Оцените материал:
Настоящий материал опубликован пользователем Алеевская Татьяна Петровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 18877
- Всего материалов: 33
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Время чтения: 0 минут
Каждый второй ребенок в школе подвергался психической агрессии
Время чтения: 3 минуты
В приграничных пунктах Брянской области на день приостановили занятия в школах
Время чтения: 0 минут
Ленобласть распределит в школы прибывающих из Донбасса детей
Время чтения: 1 минута
Курские власти перевели на дистант школьников в районах на границе с Украиной
Время чтения: 1 минута
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
🎬 Видео
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

Алгебра 10 класс (Урок№3 - Квадратные уравнения, неравенства и их системы.)Скачать

Как решать квадратные уравнения без дискриминантаСкачать

Уравнения, сводящиеся к квадратным. Биквадратное уравнениеСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Решение тригонометрических уравнений. Практическая часть. 10 класс.Скачать

Как решить симметрическое уравнение | Сведение к квадратному | Замена переменнойСкачать