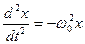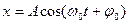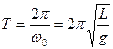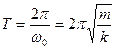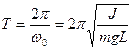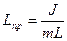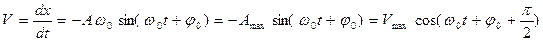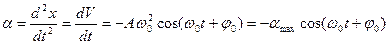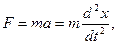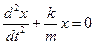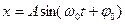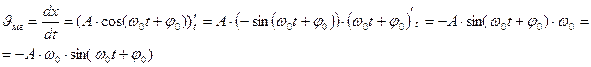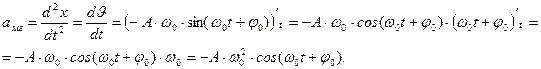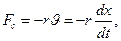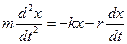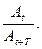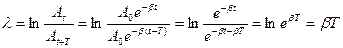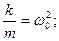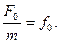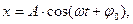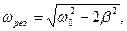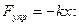Уравнения свободных незатухающих колебаний дифференциальное уравнение и его решение

Здесь х — смещение колеблющейся материальной точки, t — время,

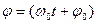
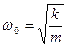
где А — амплитуда колебаний, фаза колебаний, φ₀ — начальная фаза колебаний φ= φ₀ при t=0, ω₀— круговая частота колебаний.

, где k — коэффициент квази­упругой силы (F= — kx), возникающей в системе при выходе ее из положения равновесия.

Период колебаний:

где L — длина маятника, g — ускорение свободного падения;

где k — жесткость пружины;

где J — момент инерции физического маятника относительно оси, проходящей через точку подвеса; L— расстояние между точкой подвеса и центром массы маятника.

Приведенная длина физического маятника

Скорость материальной точки, совершающей гармонические ко­лебания,

где Aω₀=V_max –амплитуда скорости.

Ускорение материальной точки при гармонических колебаниях:

где 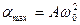-амплитуда ускорения.

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Лекция № 5 Свободные электромагнитные колебания

СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ

Выписка из рабочей программы дисциплины «Колебания и волны» – 010900

2.1 Свободные электромагнитные колебания.

Колебательный контур. Процессы в идеализированном колебательном контуре. Электромагнитные гармонические колебания. Дифференциальное уравнение свободных незатухающих электромагнитных колебаний и его решение. Собственная частота свободных электромагнитных колебаний. Формула Томсона. Закон сохранения и превращения энергии в идеализированном колебательном контуре.

1. Свободные электромагнитные колебания

Электромагнитные колебания представляют собой взаимосвязанные периодические изменения зарядов, токов, характеристик электрического и магнитного полей, сопровождающиеся взаимными превращениями этих полей.

Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур – цепь, состоящая из конденсатора ёмкостью и катушки индуктивностью .

Если сопротивление контура равно нулю, колебательный контур называют идеальным. В идеальном колебательном контуре отсутствуют потери энергии, поэтому собственные колебания, возникающие в нем, являются незатухающими.

Рассмотрим процесс возникновения свободных незатухающих колебаний в идеальном колебательном контуре. Чтобы возбудить колебания, необходимо сообщить конденсатору некоторый заряд, а потом замкнуть ключ К (рис.1).

Пусть в начальный момент времени () конденсатору сообщили некоторый заряд . При этом напряжение между его обкладками , напряженность электрического поля и энергия электрического поля – максимальны, а ток в цепи отсутствует (рис. 2,а). Затем начинается разряд конденсатора. Возникающий при этом разрядный ток, проходя через катушку , создает в ней изменяющееся магнитное поле, которое продолжает расти до тех пор, пока ток не достигает максимального значения . При этом вся энергия электрического поля конденсатора переходит в энергию магнитного поля катушки , а индукция магнитного поля достигает максимума (рис. 2,б). Несмотря на то, что конденсатор полностью разрядился, ток в колебательном контуре не прекращается и поддерживается э. д.с. самоиндукции, что в итоге приведет к перезарядке конденсатора. При этом заряд конденсатора, напряжение между обкладками, напряженность и энергия электрического поля вновь достигают максимальных значений, однако полярность обкладок конденсатора и направление напряженности электрического поля между ними противоположны тем, какие были в начальный момент времени (рис. 2, в). По окончании перезарядки энергия магнитного поля катушки перейдет в энергию электрического поля конденсатора. Начиная с этого момента, ток в контуре меняет направление, и процесс воспроизводится в обратном направлении (рис. 2, г). Система возвращается в исходное состояние (рис. 2, д), и начинается следующий период колебаний.

В контуре возникают электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот. Рисунок 2 представляет собой график зависимости заряда конденсатора от времени , , на котором значениям заряда в моменты времени сопоставлены соответствующие состояния колебательного

контура (а; б; в; г; д).

Так как сопротивление контура равно нулю, т. е. нет потерь энергии, такой процесс должен продолжаться бесконечно, а возникающие колебания называются собственными или свободными.

Период собственных незатухающих колебаний в колебательном контуре определяется формулой Томсона

, (5)

а циклическая частота

. (6)

Колебания заряда происходят по гармоническому закону

, (7)

где – максимальный заряд на обкладках конденсатора;

– циклическая частота собственных колебаний;

– начальная фаза.

На рисунках 3 и 4 представлены соответственно идеальный колебательный контур и график зависимости при .

Очевидно, что изменение напряжения между обкладками описывается таким же законом

(8)

где – максимальное напряжение между обкладками конденсатора.

Так как электрический ток характеризует скорость изменения заряда на обкладках конденсатора,

(9)

где – амплитуда силы тока.

Из выражений (7), (8), (9) следует, что колебания заряда (напряжения) и тока в контуре сдвинуты по фазе на , т. е. ток достигает максимального значения в те моменты времени, когда заряд и напряжение на обкладках конденсатора равны нулю, и наоборот. Этот же вывод следует из анализа рис. 2 (а, б, в, г, д).

Идеальный колебательный контур (рис. 3), в котором происходят свободные незатухающие электромагнитные колебания, представляет собой электрическую цепь, состоящую из конденсатора емкостью и катушки индуктивности . Запишем для этого замкнутого контура второе правило Кирхгофа: сумма падений напряжений равна сумме э. д.с., действующих в контуре.

В контуре действует только одна э. д.с. – э. д.с. самоиндукции, следовательно

,

где – падение напряжения на конденсаторе;

– мгновенное значение заряда на обкладках конденсатора;

.

Так как , , то дифференциальное уравнение свободных незатухающих электромагнитных колебаний может быть записано в виде

,

,

где – собственная циклическая частота контура.

Уравнение колебаний принимает вид

и называется уравнением свободных незатухающих электромагнитных колебаний в дифференциальной форме.

Из математики известно, что решение этого уравнения имеет вид

,

т. е. соответствует формуле (7) и рис. 4 (при ).

Таким образом, свободные незатухающие электромагнитные колебания являются гармоническими, а их период определяется формулой Томсона:

2. Закон сохранения и превращения энергии в идеализированном колебательном контуре

Исключительно важным является вопрос об энергии гармонических колебаний. С энергетической точки зрения гармоническое колебание представляет собой непрерывный процесс перехода кинетической энергии движущихся частей осциллятора в потенциальную энергию упругого элемента. Полная энергия гармонического осциллятора есть величина постоянная, так как для него потерь нет. Она равна либо максимальной кинетической энергии ( в момент прохождения положения равновесия) , либо максимальной потенциальной энергии (при амплитудном смешении). В задачах используются именно эти энергии, так как с их помощью можно оценить величину амплитуды и частоты собственных колебаний осциллятора.

Расчет энергии W гармонического осциллятора осуществляют стандартным образом. Для механических осцилляторов:

Видео:Урок 327. Гармонические колебанияСкачать

Вывод дифференциального уравнения свободного колебания

На тело, совершающее свободные колебания, действуют две силы:

1. Сила, определяемая по второму закону Ньютона:

где m – масса тела;

а – ускорение;

х – смещение;

t – время.

2. Сила упругости, выраженная по закону Гука:

где k – коэффициент упругости. Знак минус показывает, что сила упругости F_упр всегда направлена в сторону положения равновесия.

На основании второго закона Ньютона (произведение массы тела на его ускорение равно сумме всех действующих сил) получаем:

.

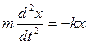
Перенесем –kx в левую часть равенства, получим:

.

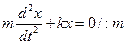
Введем замену: ,

где ω₀ – круговая (циклическая) частота колебаний (ω₀=2πν)

Получили дифференциальное уравнение второго порядка относительно смещения х.

Решением этого уравнения будет:

или (см. рис.1 и рис. 2).

,

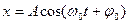
где А – амплитуда колебания;

φ₀ – начальная фаза;

ω₀t+φ₀ – фаза колебания в момент времени t;

ω₀t= ∆φ – изменение фазы колебания за время t.

Выведем уравнения мгновенной скорости и мгновенного ускорения, если колебания совершаются по закону косинуса.

Затухающие колебания.

Все реальные гармонические колебания происходят при воздействии сил сопротивления, на преодоление которых тело затрачивает часть своей энергии, в результате амплитуда колебания уменьшается со временем, т.е. колебания носят затухающий характер.

Представим график затухающего колебания:

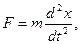
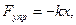
Вывод дифференциального уравнения затухающего колебания.На тело, кроме силы силы упругости действует сила сопротивления:

где r – коэффициент сопротивления.

Согласно второму закону Ньютона можно записать:

.

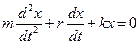
Разделим на массу m, получим:

.

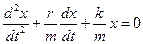
Введем обозначения: ,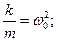

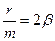
где β – коэффициент затухания.

Получили дифференциальное уравнение затухающего колебания:

.

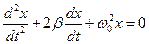
Решение уравнения существенно зависит от знака разности ,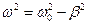

где ω— круговая частота затухающих колебаний, ω₀ — круговая частота собственных колебаний системы (без затухания).

При ω>0 решение дифференциального уравнения будет следующим:

.

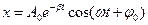
Амплитуда затухающего колебания в любой момент времени t определяется равенством:

,

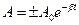
где А₀ – начальная амплитуда, указанная на графике (см. рис 3).

Период Т затухающих колебаний определяется по формуле:

.

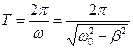
Скорость затухания (быстрота уменьшения амплитуды) определяется величиной коэффициента затухания β: чем больше β, тем быстрее уменьшается амплитуда.

Для характеристики скорости затухания ввели понятие декремента затухания.

Декрементом затухания называется отношение двух соседних амплитуд, разделенных периодом:

На практике степень затухания характеризуется логарифмическим декрементомзатухания λ, равным:

Выведем формулу, связывающую логарифмический декремент затухания λ с коэффициентом затухания β и периодом колебания Т.

.

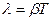
Выведем размерность коэффициента затухания

.

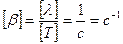
Вынужденные колебания. Вынужденными колебанияминазываются колебания, возникающие в системе при воздействии на неё внешней силы, изменяющейся по периодическому закону.

Пусть на систему действует сила:

где F₀ – максимальное значение,

ω — круговая частота колебаний внешней силы.

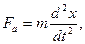
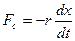
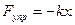
На систему действуют сила сила сопротивления и сила упругости .

С учетом всех четырех сил на основании второго закона Ньютона запишем:

.

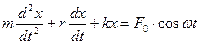
Разделим обе части равенства на m, получим:

.

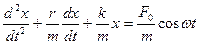
Получили дифференциальное уравнение вынужденного колебания:

.

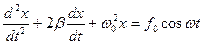
Представим график вынужденных колебаний:

В начале амплитуда колебаний возрастает, а затем становится постоянной А.

Для установившихся вынужденных колебаний:

(см. рис. 4)

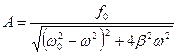
Резонанс.Если ω₀ и β для системы заданы, то амплитуда А вынужденных колебаний имеет максимальное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной. Достижение максимальной амплитуды вынужденных колебаний для заданных ω₀ и β называется резонансом.

Резонансная круговая частота определяется формулой:

а резонансная амплитуда:

.

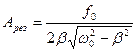
Если отсутствует сопротивление (β=0), то амплитуда неограниченно возрастает.

Представим на графиках зависимость амплитуды вынужденных колебаний от круговой частоты вынуждающей силы ω при различных значениях коэффициента затухания:

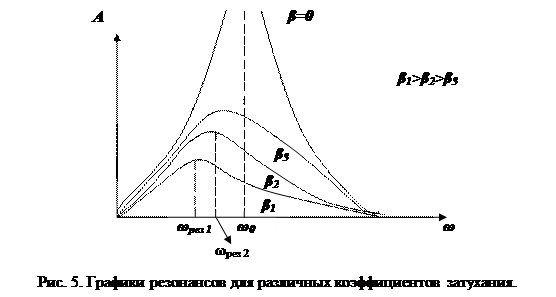По виду резонансной кривой резонанс может быть острым при β→0, тупым – при β→1. (см. рис. 5).

По механизму возбуждения резонанс классифицируется на:

— механический; акустический; электромагнитный; парамагнитный; ядерномагнитный.

Возникновение резонансных явлений в организме может быть как полезным, так и вредным. Например, на акустическом резонансе основано восприятия звука, инфразвук может вызвать разрыв тканей внутренних органов.

Автоколебания.При затухающих колебаниях энергия системы расходуется на преодоление сопротивления среды. Если восполнять эту потерю энергии, то колебания станут незатухающими. Пополнять эту потерянную системой энергию можно за счет источника энергии извне, а можно сделать так, чтобы колеблющаяся система сама бы управляла внешним воздействием.

Незатухающие колебания, возникающие в системе за счет источника энергии, не обладающего колебательными свойствами, называются автоколебаниями, а сами системы – автоколебательными.

Классическим примером автоколебаний являются часы: заведенная пружина; поднятая гиря – источник энергии; анкер – регулятор поступления энергии от источника; маятник или баланс – колебательная система.

Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы.

Автоколебания осуществляется по следующей схеме:

Через канал обратной связи регулятор, получив информацию о состоянии колебательной системы, осуществляет регулирующую подачи энергии от источника к системе.

К автоколебательным системам относятся сердце, легкие и т.д.

Автоколебательная система сердца может быть представлена в следующем виде:

Порядок выполнения работы:

1. Включить кимограф, записать положение равновесия.
2. Отклонив маятник в сторону, отпустить его, одновременно включив секундомер.
3. После записи последнего n-го колебания отключить секундомер.
4. После последнего колебания зарегистрировать положение равновесия и отключить кимограф.
5. Записать графики 3-го – 5-го колебательных процессов.
6. С помощью линейки для каждого графика определить величину начальной амплитуды (А₀) и последней амплитуды (А_n).
7. Подсчитать число полных колебаний на графике (n).
8. Определить период колебания T:

где t – время по секундомеру.

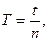
1. Определить величину коэффициента затухания по формуле:

.

1. Определить величину логарифмического декремента затухания: .
2. Полученные данные занести в таблицу.

Контрольные вопросы

1. Определения и единицы измерения основных характеристик колебательного движения.
2. Гармонические колебания. Вывод дифференциального уравнения гармонического колебания и его решение.
3. Затухающие колебания. Вывод дифференциального уравнения затухающего колебания и его решение.
4. Декремент затухания, логарифмический декремент затухания. Вывод формулы, связывающей логарифмический декремент с периодом колебания и коэффициентом затухания.
5. Вынужденные колебания. Дифференциальное уравнение вынужденного колебания и его решение.
6. Резонанс и его значение в медицине.
7. Автоколебания.

Тестовые задания

1. Циклической (круговой) частотой называется число полных колебаний за:

а) 1 с; б) 1 мин; в) 1 ч; г) 2π с.

1. Укажите формулу, связывающую циклическую частоту ω с частотой ν:

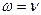
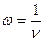
а) ; в) ;

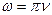
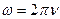
б) ; г) .

1. Укажите формулу, по которой определяется амплитуда затухающего колебания в любой момент времени t:

а) 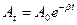; в) ;

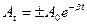
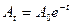
б) . г) .

1. Декрементом затухания называется отношение:

а) двух соседних амплитуд;

б) двух соседних амплитуд, разделенных периодом;

в) первой и последней амплитуд;

г) двух амплитуд, разделенных полупериодом.

1. Укажите единицу измерения коэффициента затухания β:

б) безразмерная величина; г) .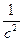

6. Укажите решение дифференциального уравнения свободного гармонического колебания:

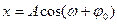
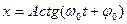
а) ; в) ;

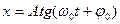
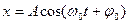
б) ; г) .

7. Укажите, сколько сил действует на систему, если она совершает свободные гармонические колебания:

8. Укажите дифференциальное уравнение свободного гармонического колебания:

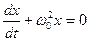
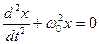
а) ; в) ;

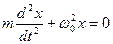
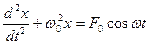
б) ; г) .

9. Укажите решение дифференциального уравнения затухающего колебания:

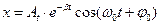
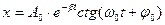
а) ; в) ;

б) 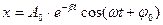; г) .

10. Сколько полных колебаний тело должно совершить в одну минуту, чтобы частота его колебаний равнялась 1 Гц:

11. Укажите подстановку в уравнение смещения затухающего колебания:

:

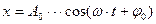
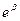
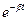
а) ; в) ;

б) ; г) ;

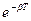
12. Укажите, сколько сил действует на систему, если она совершает вынужденные колебания:

13. Укажите дифференциальное уравнение вынужденного колебания:

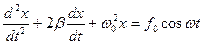
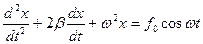
а) ; в) ;

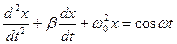
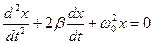
б) ; г) .

14. Укажите блок – схему, по которой осуществляются автоколебания:

15. Укажите формулу, связывающую логарифмический декремент затухания λ с периодом колебания Т и коэффициентом затухания β:

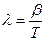
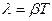
а) ; в) ;

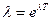
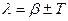
б) ; г) .

16. Укажите дифференциальное уравнение затухающего колебания:

а) ; в) ;

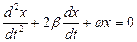
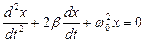
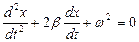
б) ; г) .

17. Укажите, по какой формуле определяется период колебания Т, если за время t тело совершило n полных колебаний:

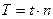
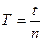
а) ; в) ;

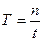
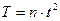
б) ; г) .

18. Укажите единицу измерения логарифмического декремента затухания:

б) с 2 ; г) безразмерная величина.

19. Укажите, какой параметр в уравнении смещения указывает на то, что процесс носит затухающий характер:

20. Укажите, какая сила вызывает уменьшение амплитуды при затухающих колебаниях:

а) ускоряющая сила;

б) сила упругости;

в) сила сопротивления;

г) сила давления.

21. Укажите, при каком значении декремента затухания процесс затухания будет проходить наиболее медленно:

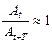
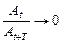
а) ; в) ;

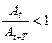
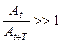
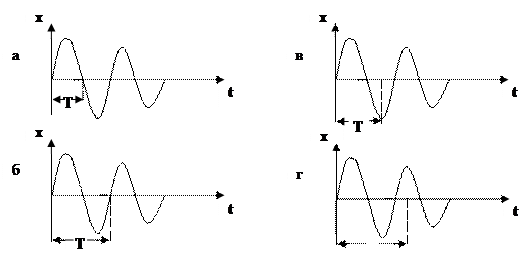
б) ; г) .

22. Укажите, на каком из графиков показан период колебания Т:

23. Укажите график вынужденного колебания:

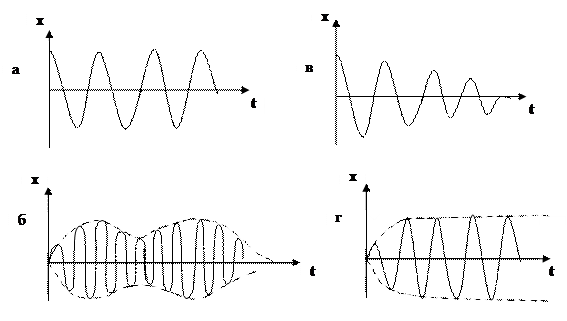24. Укажите, каков физический смысл знака «-» в формуле закона Гука

а) физический смысл отсутствует;

б) показывает, что направления силы упругости F_упр и смещения х совпадают;

в) показывает, что направления силы упругости F_упр и смещения х противоположны;

г) показывает, что направления силы упругости F_упр и смещения х взаимно перпендикулярны.

25. Частотой колебания ν называется величина, показывающая число полных колебаний:

а) за минуту; в) за час;

б) за секунду; г) за сутки.

26. Укажите, в каких единицах измеряется циклическая частота ω:

а) в секундах; в) в минутах;

б) в Гц ; г) в часах.

27. Укажите условие резонанса при β=0:

🎦 Видео

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения. 11 класс.Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

ДУ Уравнения, не разрешенные относительно производнойСкачать

Дифференциальные уравнения, 7 урок, Дифференциальные уравнения, допускающие понижение порядкаСкачать

70. Затухающие колебанияСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

1. Что такое дифференциальное уравнение?Скачать

Дифференциальные уравнения, 6 урок, Уравнения в полных дифференциалахСкачать

Честный вывод уравнения колебанийСкачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Уравнение колебаний без потерьСкачать

71. Вынужденные колебанияСкачать

Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать