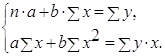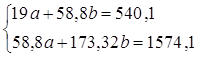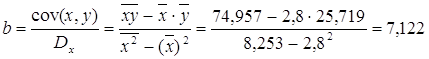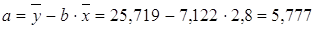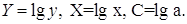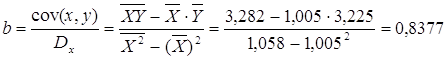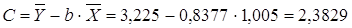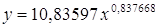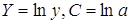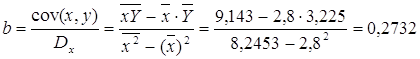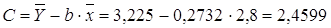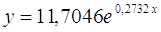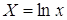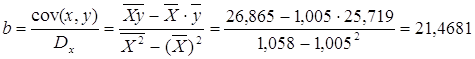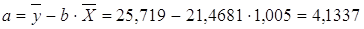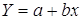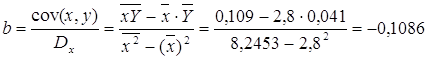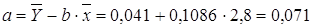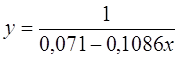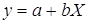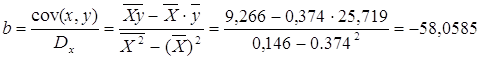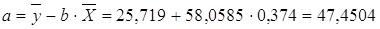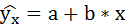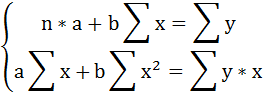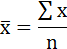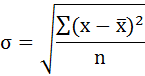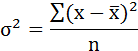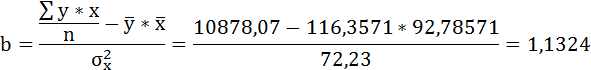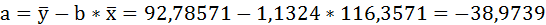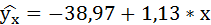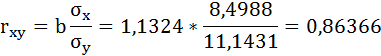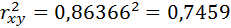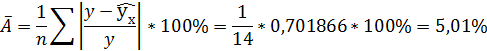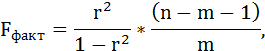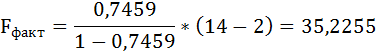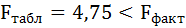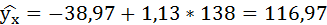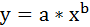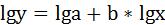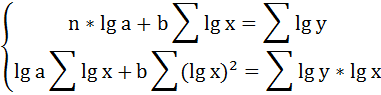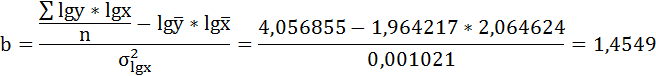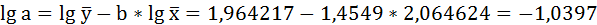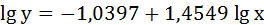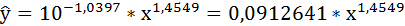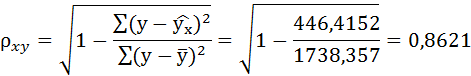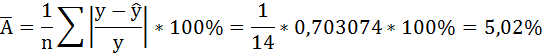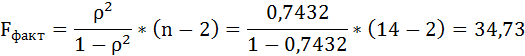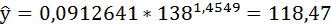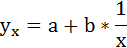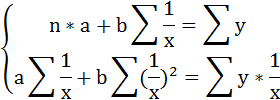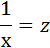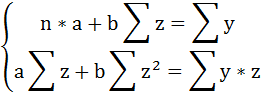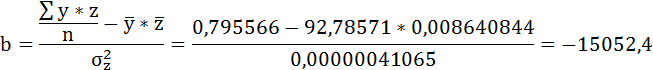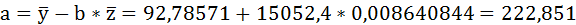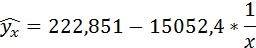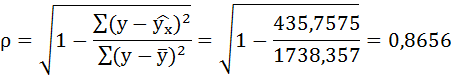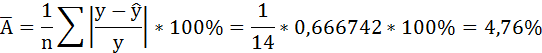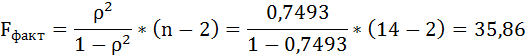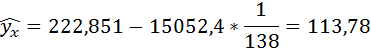Уравнения степенной и показательной регрессии (6 видео)

Содержание

Уравнение нелинейной регрессии
Виды нелинейной регрессии
Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий
Задача №1 Построение уравнения регрессии
Требуется:
Решение:
💡 Видео

Видео:Эконометрика. Линейная парная регрессияСкачать

Уравнение нелинейной регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

Видео:Эконометрика. Нелинейная регрессия. Степенная функция.Скачать

Виды нелинейной регрессии

Вид	Класс нелинейных моделей
Полиномальное уравнение регрессии: y = a + bx + cx 2 (см. метод выравнивания) Гиперболическое уравнение регрессии: Квадратичное уравнение регрессии:	Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам
Показательное уравнение регрессии: Экспоненциальное уравнение регрессии: Степенное уравнение регрессии: Полулогарифмическое уравнение регрессии: y = a + b lg(x)	Нелинейные по оцениваемым параметрам

Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.

Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.

Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .

Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .

Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):

Замена переменных.
Логарифмирование обеих частей уравнения.
Комбинированный.

y = f(x)	Преобразование	Метод линеаризации
y = b x a	Y = ln(y); X = ln(x)	Логарифмирование
y = b e ax	Y = ln(y); X = x	Комбинированный
y = 1/(ax+b)	Y = 1/y; X = x	Замена переменных
y = x/(ax+b)	Y = x/y; X = x	Замена переменных. Пример
y = aln(x)+b	Y = y; X = ln(x)	Комбинированный
y = a + bx + cx 2	x₁ = x; x₂ = x 2	Замена переменных
y = a + bx + cx 2 + dx 3	x₁ = x; x₂ = x 2 ; x₃ = x 3	Замена переменных
y = a + b/x	x₁ = 1/x	Замена переменных
y = a + sqrt(x)b	x₁ = sqrt(x)	Замена переменных

Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:

Построить поле корреляции и сформулировать гипотезу о форме связи.
Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
Оценить тесноту связи с помощью показателей корреляции и детерминации.
Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
Оценить с помощью средней ошибки аппроксимации качество уравнений.
Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
Оценить полученные результаты, выводы оформить в аналитической записке.

Год	Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y	Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х
1995	872	515,9
2000	3813	2281,1
2001	5014	3062
2002	6400	3947,2
2003	7708	5170,4
2004	9848	6410,3
2005	12455	8111,9
2006	15284	10196
2007	18928	12602,7
2008	23695	14940,6
2009	25151	16856,9

Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x

Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626

Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706

Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535

Видео:СТЕПЕННАЯ ФУНКЦИЯ график степенной функцииСкачать

Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий

2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.

· Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:

По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x 2 , ∑y 2 (табл. 2):

№ региона	X	Y	XY	X^2	Y^2	Y^cp	Y-Y^cp	Ai
1	2,800	28,000	78,400	7,840	784,000	25,719	2,281	0,081
2	2,400	21,300	51,120	5,760	453,690	22,870	-1,570	0,074
3	2,100	21,000	44,100	4,410	441,000	20,734	0,266	0,013
4	2,600	23,300	60,580	6,760	542,890	24,295	-0,995	0,043
5	1,700	15,800	26,860	2,890	249,640	17,885	-2,085	0,132
6	2,500	21,900	54,750	6,250	479,610	23,582	-1,682	0,077
7	2,400	20,000	48,000	5,760	400,000	22,870	-2,870	0,144
8	2,600	22,000	57,200	6,760	484,000	24,295	-2,295	0,104
9	2,800	23,900	66,920	7,840	571,210	25,719	-1,819	0,076
10	2,600	26,000	67,600	6,760	676,000	24,295	1,705	0,066
11	2,600	24,600	63,960	6,760	605,160	24,295	0,305	0,012
12	2,500	21,000	52,500	6,250	441,000	23,582	-2,582	0,123
13	2,900	27,000	78,300	8,410	729,000	26,431	0,569	0,021
14	2,600	21,000	54,600	6,760	441,000	24,295	-3,295	0,157
15	2,200	24,000	52,800	4,840	576,000	21,446	2,554	0,106
16	2,600	34,000	88,400	6,760	1156,000	24,295	9,705	0,285
17	3,300	31,900	105,270	10,890	1017,610	29,280	2,620	0,082
19	3,900	33,000	128,700	15,210	1089,000	33,553	-0,553	0,017
20	4,600	35,400	162,840	21,160	1253,160	38,539	-3,139	0,089
21	3,700	34,000	125,800	13,690	1156,000	32,129	1,871	0,055
22	3,400	31,000	105,400	11,560	961,000	29,992	1,008	0,033
Итого	58,800	540,100	1574,100	173,320	14506,970	540,100	0,000
сред значение	2,800	25,719	74,957	8,253	690,808	0,085
станд. откл	0,643	5,417

Система нормальных уравнений составит:

Ур-ие регрессии: = 5,777+7,122∙x. Данное уравнение показывает, что с увеличением среднедушевого денежного дохода в месяц на 1 тыс. руб. доля розничных продаж телевизоров повышается в среднем на 7,12%.

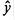
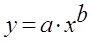
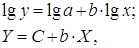
· Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:

где

Для расчетов используем данные табл. 3:

№ рег	X	Y	XY	X^2	Y^2	Yp^cp	y^cp
1	1,030	3,332	3,431	1,060	11,104	3,245	25,67072
2	0,875	3,059	2,678	0,766	9,356	3,116	22,56102
3	0,742	3,045	2,259	0,550	9,269	3,004	20,17348
4	0,956	3,148	3,008	0,913	9,913	3,183	24,12559
5	0,531	2,760	1,465	0,282	7,618	2,827	16,90081
6	0,916	3,086	2,828	0,840	9,526	3,150	23,34585
7	0,875	2,996	2,623	0,766	8,974	3,116	22,56102
8	0,956	3,091	2,954	0,913	9,555	3,183	24,12559
9	1,030	3,174	3,268	1,060	10,074	3,245	25,67072
10	0,956	3,258	3,113	0,913	10,615	3,183	24,12559
11	0,956	3,203	3,060	0,913	10,258	3,183	24,12559
12	0,916	3,045	2,790	0,840	9,269	3,150	23,34585
13	1,065	3,296	3,509	1,134	10,863	3,275	26,4365
14	0,956	3,045	2,909	0,913	9,269	3,183	24,12559
15	0,788	3,178	2,506	0,622	10,100	3,043	20,97512
16	0,956	3,526	3,369	0,913	12,435	3,183	24,12559
17	1,194	3,463	4,134	1,425	11,990	3,383	29,4585
19	1,361	3,497	4,759	1,852	12,226	3,523	33,88317
20	1,526	3,567	5,443	2,329	12,721	3,661	38,90802
21	1,308	3,526	4,614	1,712	12,435	3,479	32,42145
22	1,224	3,434	4,202	1,498	11,792	3,408	30,20445
итого	21,115	67,727	68,921	22,214	219,361	67,727	537,270
сред зн	1,005	3,225	3,282	1,058	10,446	3,225
стан откл	0,216	0,211

Рассчитаем С и b:

Получим линейное уравнение: 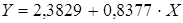. Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y.

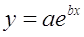
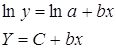
· Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:

где

Для расчетов используем данные табл. 4:

№ региона	X	Y	XY	X^2	Y^2	Yp	y^cp
1	2,800	3,332	9,330	7,840	11,104	3,225	25,156
2	2,400	3,059	7,341	5,760	9,356	3,116	22,552
3	2,100	3,045	6,393	4,410	9,269	3,034	20,777
4	2,600	3,148	8,186	6,760	9,913	3,170	23,818
5	1,700	2,760	4,692	2,890	7,618	2,925	18,625
6	2,500	3,086	7,716	6,250	9,526	3,143	23,176
7	2,400	2,996	7,190	5,760	8,974	3,116	22,552
8	2,600	3,091	8,037	6,760	9,555	3,170	23,818
9	2,800	3,174	8,887	7,840	10,074	3,225	25,156
10	2,600	3,258	8,471	6,760	10,615	3,170	23,818
11	2,600	3,203	8,327	6,760	10,258	3,170	23,818
12	2,500	3,045	7,611	6,250	9,269	3,143	23,176
13	2,900	3,296	9,558	8,410	10,863	3,252	25,853
14	2,600	3,045	7,916	6,760	9,269	3,170	23,818
15	2,200	3,178	6,992	4,840	10,100	3,061	21,352
16	2,600	3,526	9,169	6,760	12,435	3,170	23,818
17	3,300	3,463	11,427	10,890	11,990	3,362	28,839
19	3,900	3,497	13,636	15,210	12,226	3,526	33,978
20	4,600	3,567	16,407	21,160	12,721	3,717	41,140
21	3,700	3,526	13,048	13,690	12,435	3,471	32,170
22	3,400	3,434	11,676	11,560	11,792	3,389	29,638
Итого	58,800	67,727	192,008	173,320	219,361	67,727	537,053
сред зн	2,800	3,225	9,143	8,253	10,446
стан откл	0,643	0,211

Рассчитаем С и b:

Получим линейное уравнение: 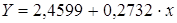. Выполнив его потенцирование, получим:

Для расчета теоретических значений y подставим в уравнение 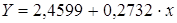значения x.

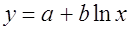
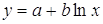
· Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем замены:

где

Для расчетов используем данные табл. 5:

№ региона	X	Y	XY	X^2	Y^2	y^cp
1	1,030	28,000	28,829	1,060	784,000	26,238
2	0,875	21,300	18,647	0,766	453,690	22,928
3	0,742	21,000	15,581	0,550	441,000	20,062
4	0,956	23,300	22,263	0,913	542,890	24,647
5	0,531	15,800	8,384	0,282	249,640	15,525
6	0,916	21,900	20,067	0,840	479,610	23,805
7	0,875	20,000	17,509	0,766	400,000	22,928
8	0,956	22,000	21,021	0,913	484,000	24,647
9	1,030	23,900	24,608	1,060	571,210	26,238
10	0,956	26,000	24,843	0,913	676,000	24,647
11	0,956	24,600	23,506	0,913	605,160	24,647
12	0,916	21,000	19,242	0,840	441,000	23,805
13	1,065	27,000	28,747	1,134	729,000	26,991
14	0,956	21,000	20,066	0,913	441,000	24,647
15	0,788	24,000	18,923	0,622	576,000	21,060
16	0,956	34,000	32,487	0,913	1156,000	24,647
17	1,194	31,900	38,086	1,425	1017,610	29,765
19	1,361	33,000	44,912	1,852	1089,000	33,351
20	1,526	35,400	54,022	2,329	1253,160	36,895
21	1,308	34,000	44,483	1,712	1156,000	32,221
22	1,224	31,000	37,937	1,498	961,000	30,406
Итого	21,115	540,100	564,166	22,214	14506,970	540,100
сред зн	1,005	25,719	26,865	1,058	690,808
стан откл	0,216	5,417

Рассчитаем a и b:

Получим линейное уравнение: .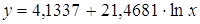

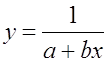
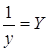
· Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель к линейному виду, заменив , тогда

Для расчетов используем данные табл. 6:

№ региона	X	Y	XY	X^2	Y^2	Y^cp
1	2,800	0,036	0,100	7,840	0,001	24,605
2	2,400	0,047	0,113	5,760	0,002	22,230
3	2,100	0,048	0,100	4,410	0,002	20,729
4	2,600	0,043	0,112	6,760	0,002	23,357
5	1,700	0,063	0,108	2,890	0,004	19,017
6	2,500	0,046	0,114	6,250	0,002	22,780
7	2,400	0,050	0,120	5,760	0,003	22,230
8	2,600	0,045	0,118	6,760	0,002	23,357
9	2,800	0,042	0,117	7,840	0,002	24,605
10	2,600	0,038	0,100	6,760	0,001	23,357
11	2,600	0,041	0,106	6,760	0,002	23,357
12	2,500	0,048	0,119	6,250	0,002	22,780
13	2,900	0,037	0,107	8,410	0,001	25,280
14	2,600	0,048	0,124	6,760	0,002	23,357
15	2,200	0,042	0,092	4,840	0,002	21,206
16	2,600	0,029	0,076	6,760	0,001	23,357
17	3,300	0,031	0,103	10,890	0,001	28,398
19	3,900	0,030	0,118	15,210	0,001	34,844
20	4,600	0,028	0,130	21,160	0,001	47,393
21	3,700	0,029	0,109	13,690	0,001	32,393
22	3,400	0,032	0,110	11,560	0,001	29,301
Итого	58,800	0,853	2,296	173,320	0,036	537,933
сред знач	2,800	0,041	0,109	8,253	0,002
стан отклон	0,643	0,009

Рассчитаем a и b:

Получим линейное уравнение: 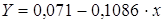. Выполнив его потенцирование, получим:

Для расчета теоретических значений y подставим в уравнение 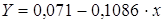значения x.

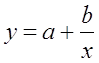
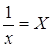
· Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы к линейному виду, заменив , тогда

Для расчетов используем данные табл. 7:

№ региона	X=1/z	Y	XY	X^2	Y^2	Y^cp
1	0,357	28,000	10,000	0,128	784,000	26,715
2	0,417	21,300	8,875	0,174	453,690	23,259
3	0,476	21,000	10,000	0,227	441,000	19,804
4	0,385	23,300	8,962	0,148	542,890	25,120
5	0,588	15,800	9,294	0,346	249,640	13,298
6	0,400	21,900	8,760	0,160	479,610	24,227
7	0,417	20,000	8,333	0,174	400,000	23,259
8	0,385	22,000	8,462	0,148	484,000	25,120
9	0,357	23,900	8,536	0,128	571,210	26,715
10	0,385	26,000	10,000	0,148	676,000	25,120
11	0,385	24,600	9,462	0,148	605,160	25,120
12	0,400	21,000	8,400	0,160	441,000	24,227
13	0,345	27,000	9,310	0,119	729,000	27,430
14	0,385	21,000	8,077	0,148	441,000	25,120
15	0,455	24,000	10,909	0,207	576,000	21,060
16	0,385	34,000	13,077	0,148	1156,000	25,120
17	0,303	31,900	9,667	0,092	1017,610	29,857
19	0,256	33,000	8,462	0,066	1089,000	32,564
20	0,217	35,400	7,696	0,047	1253,160	34,829
21	0,270	34,000	9,189	0,073	1156,000	31,759
22	0,294	31,000	9,118	0,087	961,000	30,374
Итого	7,860	540,100	194,587	3,073	14506,970	540,100
сред знач	0,374	25,719	9,266	0,146	1318,815
стан отклон	0,079	25,639

Рассчитаем a и b:

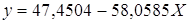
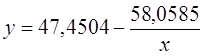
Получим линейное уравнение: . Получим уравнение регрессии: .

3. Оценка тесноты связи с помощью показателей корреляции и детерминации:

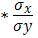
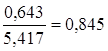
· Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции r_xy=b=7,122*, что говорит о прямой сильной связи фактора и результата. Коэффициент детерминации r²_xy=(0,845)²=0,715. Это означает, что 71,5% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

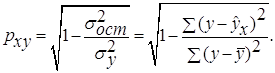
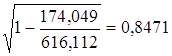
· Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции =, что говорит о очень сильной тесной связи, но немного больше чем в линейной модели. Коэффициент детерминации r²_xy=0,7175. Это означает, что 71,75% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

· Экспоненциальная модель. Был получен следующий индекс корреляции ρ_xy=0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²_xy=0,66. Это означает, что 66% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

· Полулогарифмическая модель. Был получен следующий индекс корреляции ρ_xy=0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²_xy=0,7358. Это означает, что 73,58% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

· Гиперболическая модель. Был получен следующий индекс корреляции ρ_xy=0,8448 и коэффициент корреляции r_xy=-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²_xy=0,7358. Это означает, что 73,5% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

· Обратная модель. Был получен следующий индекс корреляции ρ_xy=0,8114 и коэффициент корреляции r_xy=-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²_xy=0,6584. Это означает, что 65,84% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρ_xy=0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).

Видео:Множественная степенная регрессияСкачать

Задача №1 Построение уравнения регрессии

Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).

Индекс розничных цен на продукты питания (х)	Индекс промышленного производства (у)
1	100	70
2	105	79
3	108	85
4	113	84
5	118	85
6	118	85
7	110	96
8	115	99
9	119	100
10	118	98
11	120	99
12	124	102
13	129	105
14	132	112

Требуется:

1. Для характеристики зависимости у от х рассчитать параметры следующих функций:

В) равносторонней гиперболы.

2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.

Решение:

1. Для расчёта параметров линейной регрессии

Решаем систему нормальных уравнений относительно a и b:

Построим таблицу расчётных данных, как показано в таблице 1.

Таблица 1 Расчетные данные для оценки линейной регрессии

№ п/п	х	у	ху	x 2	y 2
1	100	70	7000	10000	4900	74,26340	0,060906
2	105	79	8295	11025	6241	79,92527	0,011712
3	108	85	9180	11664	7225	83,32238	0,019737
4	113	84	9492	12769	7056	88,98425	0,059336
5	118	85	10030	13924	7225	94,64611	0,113484
6	118	85	10030	13924	7225	94,64611	0,113484
7	110	96	10560	12100	9216	85,58713	0,108467
8	115	99	11385	13225	9801	91,24900	0,078293
9	119	100	11900	14161	10000	95,77849	0,042215
10	118	98	11564	13924	9604	94,64611	0,034223
11	120	99	11880	14400	9801	96,91086	0,021102
12	124	102	12648	15376	10404	101,4404	0,005487
13	129	105	13545	16641	11025	107,1022	0,020021
14	132	112	14784	17424	12544	110,4993	0,013399
Итого:	1629	1299	152293	190557	122267	1299,001	0,701866
Среднее значение:	116,3571	92,78571	10878,07	13611,21	8733,357	х	х
	8,4988	11,1431	х	х	х	х	х
	72,23	124,17	х	х	х	х	х

Среднее значение определим по формуле:

Cреднее квадратическое отклонение рассчитаем по формуле:

и занесём полученный результат в таблицу 1.

Возведя в квадрат полученное значение получим дисперсию:

Параметры уравнения можно определить также и по формулам:

Таким образом, уравнение регрессии:

Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.

Рассчитаем линейный коэффициент парной корреляции:

Связь прямая, достаточно тесная.

Определим коэффициент детерминации:

Вариация результата на 74,59% объясняется вариацией фактора х.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .

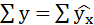
следовательно, параметры уравнения определены правильно.

Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:

В среднем расчётные значения отклоняются от фактических на 5,01%.

Оценку качества уравнения регрессии проведём с помощью F-теста.

F-тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера.

F_факт определяется по формуле:

где n – число единиц совокупности;

m – число параметров при переменных х.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза.

Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

2. Степенная регрессия имеет вид:

Для определения параметров производят логарифмирование степенной функции:

Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:

Построим таблицу расчётных данных, как показано в таблице 2.

Таблица 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у	lg x	lg y	lg x*lg y	(lg x) 2	(lg y) 2
1	100	70	2,000000	1,845098	3,690196	4,000000	3,404387
2	105	79	2,021189	1,897627	3,835464	4,085206	3,600989
3	108	85	2,033424	1,929419	3,923326	4,134812	3,722657
4	113	84	2,053078	1,924279	3,950696	4,215131	3,702851
5	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
6	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
7	110	96	2,041393	1,982271	4,046594	4,167284	3,929399
8	115	99	2,060698	1,995635	4,112401	4,246476	3,982560
9	119	100	2,075547	2,000000	4,151094	4,307895	4,000000
10	118	98	2,071882	1,991226	4,125585	4,292695	3,964981
11	120	99	2,079181	1,995635	4,149287	4,322995	3,982560
12	124	102	2,093422	2,008600	4,204847	4,382414	4,034475
13	129	105	2,110590	2,021189	4,265901	4,454589	4,085206
14	132	112	2,120574	2,049218	4,345518	4,496834	4,199295
Итого	1629	1299	28,90474	27,49904	56,79597	59,69172	54,05467
Среднее значение	116,3571	92,78571	2,064624	1,964217	4,056855	4,263694	3,861048
	8,4988	11,1431	0,031945	0,053853	х	х	х
	72,23	124,17	0,001021	0,0029	х	х	х

Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у
1	100	70	74,16448	17,34292	0,059493	519,1886
2	105	79	79,62057	0,385112	0,007855	190,0458
3	108	85	82,95180	4,195133	0,024096	60,61728
4	113	84	88,59768	21,13866	0,054734	77,1887
5	118	85	94,35840	87,57961	0,110099	60,61728
6	118	85	94,35840	87,57961	0,110099	60,61728
7	110	96	85,19619	116,7223	0,11254	10,33166
8	115	99	90,88834	65,79901	0,081936	38,6174
9	119	100	95,52408	20,03384	0,044759	52,04598
10	118	98	94,35840	13,26127	0,037159	27,18882
11	120	99	96,69423	5,316563	0,023291	38,6174
12	124	102	101,4191	0,337467	0,005695	84,90314
13	129	105	107,4232	5,872099	0,023078	149,1889
14	132	112	111,0772	0,85163	0,00824	369,1889
Итого	1629	1299	1296,632	446,4152	0,703074	1738,357
Среднее значение	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Решая систему нормальных уравнений, определяем параметры логарифмической функции.

Получим линейное уравнение:

Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 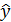. По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 5,02%.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

3. Уравнение равносторонней гиперболы

Для определения параметров этого уравнения используется система нормальных уравнений:

Произведем замену переменных

и получим следующую систему нормальных уравнений:

Решая систему нормальных уравнений, определяем параметры гиперболы.

Составим таблицу расчётных данных, как показано в таблице 3.

Таблица 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у	z	yz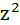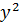
1	100	70	0,010000000	0,700000	0,0001000	4900
2	105	79	0,009523810	0,752381	0,0000907	6241
3	108	85	0,009259259	0,787037	0,0000857	7225
4	113	84	0,008849558	0,743363	0,0000783	7056
5	118	85	0,008474576	0,720339	0,0000718	7225
6	118	85	0,008474576	0,720339	0,0000718	7225
7	110	96	0,009090909	0,872727	0,0000826	9216
8	115	99	0,008695652	0,860870	0,0000756	9801
9	119	100	0,008403361	0,840336	0,0000706	10000
10	118	98	0,008474576	0,830508	0,0000718	9604
11	120	99	0,008333333	0,825000	0,0000694	9801
12	124	102	0,008064516	0,822581	0,0000650	10404
13	129	105	0,007751938	0,813953	0,0000601	11025
14	132	112	0,007575758	0,848485	0,0000574	12544
Итого:	1629	1299	0,120971823	11,13792	0,0010510	122267
Среднее значение:	116,3571	92,78571	0,008640844	0,795566	0,0000751	8733,357
	8,4988	11,1431	0,000640820	х	х	х
	72,23	124,17	0,000000411	х	х	х

Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у
1	100	70	72,3262	0,033231	5,411206	519,1886
2	105	79	79,49405	0,006254	0,244083	190,0458
3	108	85	83,47619	0,017927	2,322012	60,61728
4	113	84	89,64321	0,067181	31,84585	77,1887
5	118	85	95,28761	0,121031	105,8349	60,61728
6	118	85	95,28761	0,121031	105,8349	60,61728
7	110	96	86,01027	0,10406	99,79465	10,33166
8	115	99	91,95987	0,071112	49,56344	38,6174
9	119	100	96,35957	0,036404	13,25272	52,04598
10	118	98	95,28761	0,027677	7,357059	27,18882
11	120	99	97,41367	0,016024	2,516453	38,6174
12	124	102	101,46	0,005294	0,291565	84,90314
13	129	105	106,1651	0,011096	1,357478	149,1889
14	132	112	108,8171	0,028419	10,1311	369,1889
Итого:	1629	1299	1298,988	0,666742	435,7575	1738,357
Среднее значение:	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Значения параметров регрессии a и b составили:

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 4,76%.

По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.