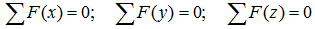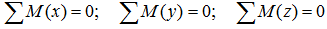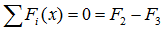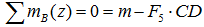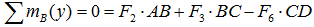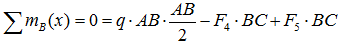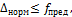Уравнения статики в строительной механике (5 видео)

iSopromat.ru

Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.

При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат

что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы

из условия отсутствия ее вращения относительно указанных осей.

Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.

Содержание

Пример составления уравнений равновесия
Суммы проекций сил
Суммы моментов
Статика сооружений (стр. 1 )
ПРЕДИСЛОВИЕ
Уравнения статики в строительной механике
💥 Видео

Видео:Определение реакций опор в балке. Сопромат.Скачать

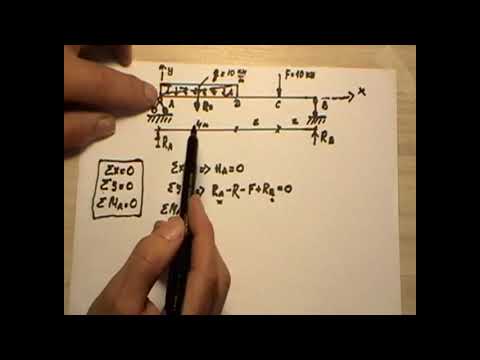
Пример составления уравнений равновесия

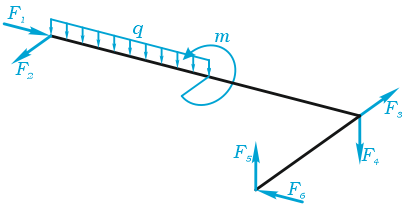
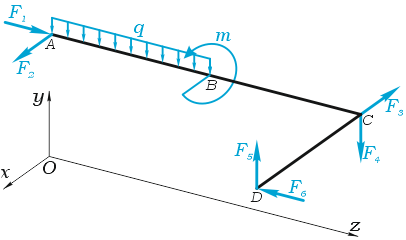
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F₁-F₆, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.

Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.

Суммы проекций сил

Сумма проекций всех сил на ось x (с учетом правила знаков для сил):

здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.

Суммы моментов

Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):

в плоскости xOy:
в плоскости xOz:
в плоскости yOz:

Из полученных шести уравнений можно определить не более шести неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Статика сооружений (стр. 1 )

Уравнения статики в строительной механике

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Нижегородский государственный архитектурно-строительный университет»

Утверждено редакционно-издательским советом

университета в качестве учебного пособия

Статика сооружений: Учебное пособие. – Н. Новгород, Нижегород. гос. архитект. — строит. ун-т, 2012г. – 94 с.

Сжато и доступно изложены основы строительной механики в рамках, не выходящих за пределы требований ГОС. В популярной форме авторы знакомят с основными понятиями и методами этой дисциплины, необходимыми для изучения статически определимых и статически неопределимых плоских стержневых систем. Рассматривается методика построения эпюр внутренних усилий и определения перемещений. Изложен метод сил и метод перемещений, даны сведения о методе конечных элементов. Изложение сопровождается примерами, необходимыми для успешного овладения теорией и приобретения минимальных навыков в решении задач.

Предназначено для студентов направления 521700 — Архитектура, но будет полезно и студентам других специальностей, изучающим основы строительной механики по сокращенной программе. Например – студентам строительного направления, специализирующимся по профилям «Теплогазоснабжение и вентиляция» или «Водоснабжение и водоотведение».

Илл. 66, библиогр. назв.7.

Видео:Определение опорных реакций в простой балке. Урок №1Скачать

ПРЕДИСЛОВИЕ

Переход к многоуровневой системе образования проходит в условиях гуманитаризации процесса обучения и создания новых информационно-вычислительных систем. Это сопровождается значительным сокращением времени, отводимого на изучение механики у студентов традиционных специальностей, и появлением новых специальностей с одним или двухсеместровым курсом по этой дисциплине.

К их числу относится и курс основ строительной механики для студентов направления 521700 — «Архитектура», который состоит из трех разделов:

— статика твердого тела,

— статика деформируемого тела,

Отметим, что студенты строительных специальностей изучают эти разделы механики в соответствующих курсах: теоретической механики, сопротивления материалов и строительной механики. Поэтому нетрудно понять, что успешное овладение основами механики в рамках сокращенной программы представляет непростую задачу, как для лектора, так и для студентов. И первым шагом на пути её решения является определение целей этого курса. Для студентов-архитекторов они сформулированы так:

— научить анализировать существующие конструктивные решения, понимать работу сооружения в целом и оценивать ту роль, которую играют отдельные элементы ансамбля, устанавливать функциональную связь между воздействиями, внутренними усилиями и формой сооружения;

— способствовать осознанному, свободному и целенаправленному решению основной задачи архитектурного проектирования – поиску новых форм и совершенных решений;

— ознакомить с основными понятиями и методами строительной механики и помочь формированию рационального и логического мышления.

Достижение намеченных целей требует тщательной подготовки учебной программы и её методического обеспечения.

Настоящее пособие является попыткой содействовать решению этой задачи для третьего раздела курса – статики сооружений. Его содержание не претендует на полноту и отражает точку зрения авторов на то, каким должен быть начальный курс этой дисциплины для архитекторов.

В частности, было принято решение ограничиться изучением плоских стержневых систем, которые в пособии представлены балками, рамами, фермами и арками. Изложена методика построения эпюр и определения перемещений, рассмотрены метод сил и метод перемещений. Даны понятия о расчете статически неопределимых систем методом конечных элементов.

Замечания в конце ряда параграфов предназначены для критически настроенных читателей и могут быть оставлены без внимания при первом чтении.

Авторы благодарят студентку факультета архитектуры и градостроительства С. Смирнову за выполненные для этого пособия рисунки.

ГЛАВА 1. ВВЕДЕНИЕ

1.1. Предмет строительной механики и ее задачи

Термин «строительная механика» применяют в широком и узком смысле этого слова.

В широком смысле – строительная механика это раздел механики, в котором ее выводы и методы применяют для решения задач проектирования, строительства и эксплуатации сооружений. В этом значении она объединяет такие науки и дисциплины как:

– статика и динамика сооружений;

– металлические и железобетонные конструкции

и многое другое. При этом термин «строительная механика» близок к понятиям «прикладная» или «техническая механика».

В узком смысле слова строительная механика – это, прежде всего, статика сооружений, в дальнейшем именно так мы и будем понимать этот термин.

Напомним, что если предметом теоретической механики является абсолютно твердое тело (или система таких тел), а предметом сопромата – деформируемое тело, то предметом строительной механики является система деформируемых тел.

Основная задача строительной механики – проектирование сооружений, находящихся в определенных условиях с учетом требований прочности, жесткости, устойчивости, надежности, экономичности, эстетики и других ограничений. Для решения этой задачи нужно построить модель сооружения, выделив основные несущие элементы и определив действующую на них нагрузку. Такая модель в виде совокупности деформируемых тел, соединенных друг с другом и с землей определенными связями, и называется расчетной схемой или системой.

В зависимости от геометрических особенностей элементов системы их делят на три класса: стержневые, тонкостенные и массивы. В общем случае расчетная схема может включать в себя каждый из этих элементов. Мы ограничимся в дальнейшем рассмотрением плоских стержневых систем.

1. Помимо основной задачи – проектирования в строительной механике, как и в сопромате, может возникнуть необходимость расчета сооружения, уже находящегося в эксплуатации. Например – при его реконструкции.

2. Решение основной задачи строительной механики сводится, прежде всего, к определению внутренних усилий. Последующий подбор сечений элементов конструкции выполняется методами сопромата либо, в зависимости от вида материала, – по теории железобетонных, металлических конструкций и т. д.

1.2. Кинематический анализ сооружений

Прежде чем приступить к расчету модели сооружения, необходимо проверить: способна ли она воспринимать приложенную нагрузку, оставаясь в равновесии? При этом расчетная схема рассматривается как совокупность не деформируемых, а абсолютно жестких тел – дисков, и в отдельный класс выделяются системы, элементы которых обладают подвижностью, то есть могут смещаться относительно друг друга или относительно земли. Такое исследование структуры модели называется ее кинематическим анализом.

Поскольку подвижность системы зависит, очевидно, от вида связей, соединяющих ее элементы, вернемся к рассмотрению и уточнению этих понятий – уже встречавшихся в теоретической механике.

1.2.1. Связи и их реакции

Напомним, что под связью понимают тело, ограничивающее свободу перемещения выбранного рассматриваемого тела, а реакцией связи называют силу, с которой связь действует на это тело.

Будем называть связь линейной, если соответствующая ей реакция – сила и моментной, если соответствующая ей реакция – момент.

Для плоских стержневых систем можно ограничиться рассмотрением следующих видов связей.

Подвижная опора (рис. 1.1) помимо обозначения по ГОСТу (рис. 1.1, а) может на схемах изображаться так, как показано на рис. 1.1, б и 1.1, в. Она соответствует одной линейной связи, а ее реакция перпендикулярна заштрихованной опорной площадке (рис. 1.1, г).

Неподвижная опора (рис. 1.2) также допускает на схемах изображения, отличные от стандартного – на рис. 1.2, а. Очевидно, что она эквивалентна двум линейным связям (рис. 1.2, в – г).

Жесткое защемление (рис. 1.3, а) исключает не только перемещения закрепленной точки балки, но и ее поворот вокруг этой точки. Оно эквивалентно двум линейным связям и одной моментной (рис. 1.3, б), либо трем линейным связям при D ® 0 (рис. 1.3, в).

Скользящее защемление (рис. 1.4, а – б) в отличие от жесткого не препятствует смещению закрепленной таким образом точки в одном из направлений и эквивалентно линейной и моментной связям (рис. 1.4, в) либо двум линейным при D ® 0 (рис. 1.4, г).

Кратный шарнир, соединяющий N дисков, (рис. 1.5, а) эквивалентен (N – 1) простому шарниру (рис. 1.5, б).

1. Результаты расчета можно улучшить, если учесть податливость соединений элементов системы.

2. Построение расчетной схемы действующего сооружения может оказаться непростой задачей, соизмеримой по сложности с самим расчетом.

1.2.2. Степени свободы и статическая определимость системы

Все системы в механике можно разделить на два класса: неизменяемые системы (НС) и изменяемые системы (ИС).

Определение 1.1. Неизменяемыми или неподвижными будем называть системы, элементы которых не могут перемещаться относительно друг друга или относительно земли, если они являются абсолютно твердыми, то есть недеформируемыми.

Изменяемыми или подвижными будем называть системы, элементы которых могут перемещаться относительно друг друга или относительно земли, оставаясь абсолютно твердыми

НС могут воспринимать любую нагрузку, ИС – только определенные виды нагрузок.

Например, рама на рис. 1.10, а является НС и может воспринимать как горизонтальную, так и вертикальную нагрузку, оставаясь в положении равновесия. А раму на рис. 1.10, б можно загрузить вертикальной нагрузкой, но она не способна воспринимать горизонтальную нагрузку, под действием которой она придет в движение – подобно незакрепленному на рельсах монтажному крану под действием ветра.

Нетрудно догадаться, что в строительстве в основном применяют неизменяемые системы – изменяемые здесь используют довольно редко и с большой осторожностью (в отличие от машиностроения, где наоборот — интерес представляют изменяемые или подвижные системы).

Все неизменяемые системы делятся на статически определимые (СОС) и статически неопределимые системы (СНС).

Напомним, что СОС – это системы, для которых число неизвестных реакций внешних и внутренних связей не превышает максимально допустимого числа уравнений статики, которые можно составить для их определения.

Если число неизвестных больше максимально допустимого числа уравнений, система называется СНС. При этом разность между числом неизвестных и числом уравнений называется степенью статической неопределимости системы.

Чтобы описать изменяемые системы введем следующее

Определение 1.2. Под степенью свободы системы – W будем понимать минимальное число параметров, определяющих ее положение в пространстве.

Очевидно, что для неподвижных систем W = 0, а для подвижных W ³ 1. Для точки на плоскости W = 2, и в качестве параметров можно выбрать ее декартовы координаты. Чтобы однозначно определить положение твердого тела (диска) на этой плоскости нужно задать уже три параметра. Например – координаты фиксированной точки A этого диска — xA , yA и угол наклона j принадлежащего ему отрезка AB (рис. 1.6). Таким образом, для диска W = 3, а система N дисков на плоскости будет иметь 3N степеней свободы.

Если два свободных диска на плоскости (W = 6) соединить одной линейной связью C1C2, получим систему с пятью степенями свободы (рис. 1.7), поскольку к трем параметрам для первого диска добавятся углы j1 и j2, определяющие положение стержня C1C2 относительно диска Д1 и диска Д2 относительно точки C2. Аналогично, система двух дисков, соединенных двумя линейными связями (или шарниром) будет иметь 4 степени свободы.

Естественно предположить, что всякое наложение дополнительной связи уменьшает степень свободы системы на единицу, поэтому для произвольной плоской системы ее можно найти по формуле:

W* = 3Д — 2Ш — СО , (1.1)

где W* – предполагаемая или условная степень свободы системы;

Д – число дисков;

Ш – число простых шарниров, соединяющих диски друг с другом;

СО – число опорных связей.

Как видим, при рассмотрении любой системы возможны три варианта:

1) W* > 0 – система заведомо подвижна;

2) W* = 0 – система имеет минимальное число связей, необходимых для ее неизменяемости;

3) W* 0, W* = 0) подразделяются на:

– геометрически изменяемые системы (ГИС);

– мгновенно изменяемые системы (МИС).

Мгновенно изменяемые отличаются от ГИС тем, что допускают не конечные – как рама на рис. 1.10, б, – а только бесконечно малые перемещения. При этом значения параметров, о которых идет речь в определении 1.4, у ГИС остаются постоянными, а у МИС – изменяются при перемещении.

Кроме того, переход неподвижных статически определимых систем в МИС может сопровождаться появлением бесконечно больших опорных реакций.

Рассмотрим, например, НС на рис. 1.11, а. Для определения опорной реакции RB составим уравнение равновесия: SМА = 0, откуда найдем: RB = Pa/D. Эта рама переходит в МИС на рис. 1.11, б при критическом значении параметра D = 0. Нетрудно видеть, что предел RB при D ® 0 равен бесконечности.

Это может привести к разрушению реальной конструкции, поэтому такие МИС не применяют в строительстве.

Термин «мгновенно изменяемая система», подчеркивает, что под действием приложенной нагрузки реальная деформируемая система может занять новую конфигурацию, для которой значение параметра станет отличным от критического. При этом в рассматриваемом примере (рис. 1.11, б) точка В сместится вниз и реакция RB примет конечное значение.

Итак, мы выяснили, что принадлежность системы к классу МИС крайне нежелательна. Поэтому перечислим некоторые признаки МИС:

1) Два диска, соединенные шарниром, связаны с остальной частью системы или с землей при помощи двух других шарниров, лежащих на одной прямой с первым (рис. 1.12).

2) Диск, прикреплен к системе или к земле при помощи трех линейных связей, у которых линии действия реакций параллельны (рис. 1.13) или пересекаются в одной точке (рис. 1.14).

1. МИС на рис. 1.11, б соответствует первому из приведенных признаков, роль второго диска выполняет подвижная опора В. Диск Д1 на рис. 1.14 выполняет роль третьей линейной связи по отношению к диску Д2.

2. Приведенные признаки МИС не являются исчерпывающими, то есть если исследуемая модель не отвечает им, то это не означает, что она не будет принадлежать к этому классу. Самым общим является аналитический метод исследования систем, основанный на рассмотрении уравнений равновесия для определения их опорных реакций.

3. Поскольку кинематический анализ связан с рассмотрением системы абсолютно твердых тел, он мог бы изучаться в курсе теоретической, а не как традиционно – строительной механики. Кстати, в [5] на стр. 26-28 можно найти несколько МИС, ошибочно включенных в задание, где требуется определить опорные реакции составной конструкции.

1.2.4. Способы образования и структурный анализ

Рассмотрим два способа образования стержневых систем, которые будут неизменяемыми и статически определимыми. Другими словами, выясним, при каких условиях соотношение:

W* = 3Д — 2Ш — СО = 0 (1.5)

будет не только необходимым, но и достаточным для образования таких систем.

1. Соединение диска с землей (соединение двух дисков). Диск прикреплен к земле при помощи шарнира и линейной связи, линия действия реакции которой не проходит через этот шарнир (рис. 1.15, а).

Шарнир А можно заменить двумя линейными связями, линии действия которых пересекаются в точке, через которую не должна проходить линия действия реакции третьей линейной связи (рис. 1.15, б).

Если диск Д2 присоединяется не к земле, а к диску Д1, получим систему, которую можно принять за новый диск, имеющий ту же степень свободы, что и диск Д1.

Этот способ образования систем называется диадным – от названия простейшей фермы, образованной из двух стержней, соединенных шарниром В. Роль первого стержня выполняет незагруженный диск АВ (рис. 1.15, а).

2. Соединение двух дисков с землей (соединение трех дисков). Два диска соединены друг с другом и с землей при помощи трех шарниров, не лежащих на одной прямой (рис. 1.16, а).

Аналогично соединяются три диска, при этом каждый шарнир можно заменить двумя линейными связями, у которых точки пересечения линий действия реакций также не должны лежать на одной прямой (рис. 1.16, б).

Этот способ образования систем называется способом трехшарнирной арки. Очевидно, что он является более общим и сводится к диадному, если диски Д1 и Д2 незагружены и, значит, их можно заменить стержнями АС и ВС, соединенными в точке С (рис. 1.16, а).

Нетрудно заметить, что ограничения, налагаемые на способы образования системы, нужны для того, чтобы избежать появления МИС.

Структурный анализ. Заключается в исследовании уже существующей системы с точки зрения возможности ее образования двумя рассмотренными способами.

– системы, образованные из нескольких дисков, образуют один новый диск;

– при условии (1.5) ни один из присоединенных дисков не должен иметь лишних связей;

– вновь образованная система будет неподвижной (НС) и статически определимой (СОС).

Пример 1.3. Выполнить структурный анализ рамы (рис. 1.17).

Решение. Система состоит из пяти дисков, соединенных простыми шарнирами E, G, F и кратным шарниром D, эквивалентным двум простым.

Условная степень свободы по формуле (1.5):

W* = 3 × 5 — 2 × 5 — 5 = 0.

Диски Д1 и Д2 образуют по способу трехшарнирной арки новый диск Д1-2, жестко связанный с землей. К диску Д1-2 диадным способом при помощи шарнира D и линейной связи C присоединяется диск Д3, который образует новый и неподвижный относительно земли диск Д1-3. Наконец, к диску Д1-3 присоединяется диада Д4, Д5, образуя диск Д1-5. Таким образом, заданная система является СОС и НС. ·

Следует отметить, что системы могут быть образованы и другими способами – отличными от диадного и способа трехшарнирной арки, поэтому основанный на них структурный анализ не является универсальным методом исследования системы. Например, с его помощью нельзя дать ответ на вопрос об изменяемости рамы на рис. 1.18, поскольку ее нельзя образовать двумя указанными способами.

1.2.5. Аналитическое исследование системы

Как уже отмечалось, этот метод исследования систем является самым общим.

Суть метода. Уравнения равновесия для определения опорных реакций исследуемой системы можно представить в виде:

где [A] – матрица коэффициентов при неизвестных;

<X> – вектор-столбец неизвестных опорных реакций;

<B> – вектор-столбец нагрузки.

При этом для СОС любому вектору <B> однозначно соответствует единственный вектор <X>, что возможно только при условии: det [A] ¹ 0.

Учитывая, что в силу (1.5) СОС одновременно являются НС, можно сделать вывод, что необходимым и достаточным условием неподвижной системы будет:

Наоборот, необходимым и достаточным условием подвижной системы является:

Таким образом, для кинематического анализа системы достаточно вычислить определитель матрицы соответствующей системы алгебраических уравнений. Но можно избежать даже этой процедуры, учитывая некоторые сложности которые она вызывает уже при четвертом порядке определителя.

Метод нулевой нагрузки. Рассмотрим однородную систему уравнений, соответствующую (1.6):

Известно, что она имеет только нулевое решение, если det [A] ¹ 0, и наоборот – условием ненулевого решения будет: det [A] = 0.

Отсюда – следующее правило:

1) Если система (1.9) имеет решение <X> = <0>, то соответствующая механическая система является неподвижной;

2) Если система (1.9) имеет решение <X> ¹ <0>, то соответствующая механическая система является подвижной.

Пример 1.4. Выполнить кинематический анализ рамы (рис. 1.18).

Решение. Воспользуемся методом нулевой нагрузки, применив графический способ решения (рис. 1.19).

Из условия равновесия диска АЕ следует, что реакции RA и RE направлены по прямой АЕ (аксиома 2).

Из условия равновесия диска EBF следует, что реакция RF проходит через точку K, где пересекаются линии действия R¢E = — RE и RB (теорема о трех силах).

Из условия равновесия диска FCG аналогично находим линию действия реакции RG, проходящей вдоль прямой GL.

Наконец, рассмотрим диск DG . По аксиоме 2 реакция RG = — RD должна быть направлена вдоль прямой GD, соединяющей точки их приложения. С другой стороны, R¢G = — RG действует по прямой GL. Одновременно удовлетворить этим требованиям можно, лишь полагая RG = 0, откуда следует, что все реакции равны нулю, а, значит, <X> = <0> и система будет неподвижной. ·

1. Подобно тому, как СНС, которые мы рассмотрим в 4 главе, могут быть статически неопределимыми внешним и внутренним образом, можно говорить о системах, изменяемых аналогично. Поэтому в общем случае вектор <X> в системе (1.6) должен содержать компоненты реакций не только внешних, но и внутренних связей.

2. Отметим, что в последнем примере 1.4 мы остаемся в рамках аналитического метода анализа геометрической изменяемости системы, несмотря на то, что при реализации метода нулевой нагрузки применялся графический способ определения реакций связей. Такой прием вполне оправдан, поскольку формальный подход потребовал бы вычисления определителя десятого порядка.

3. Анализ системы уравнений (1.6), независимо от условия (1.5), позволяет получить полную характеристику механической системы, включая степени ее свободы и статической неопределимости.

4. При построении модели сооружения ее параметры определяются с некоторой степенью точности, поэтому опасность на практике представляют не только МИС, но и близкие к ним – у которых det [A] » 0.

1.3. Основные уравнения строительной механики

Математическая сторона основной задачи строительной механики основана на зависимостях, полученных в сопромате. Напомним их на примере напряженно-деформированного состояния элемента рамы, для которого – в отличие от балки – поперечный изгиб сопровождается дополнительным растяжением или сжатием.

Пусть такой элемент длиной dx расположен в локальной системе координат Oxy, где ось Ox направлена по оси стержня, и загружен распределенной нагрузкой интенсивностью qx и qy вдоль Ox и Oy соответственно (рис. 1.20).

Напряженно-деформированное состояние стержня определяется девятью компонентами:

– деформациями (κ, g, e).

Уравнения для определения этих функций можно разделить на три группы:

Статические уравнения – связывают внутренние усилия (рис. 1.20, б) с заданной нагрузкой:

Геометрические уравнения – выражают деформации через перемещения, показанные на рис. 1.20, б, в:

Физические уравнения – представляют собой зависимости между внутренними усилиями и деформациями:

где E – модуль Юнга;

G – модуль сдвига;

F – площадь поперечного сечения стержня;

J – момент его инерции;

m – коэффициент, учитывающий неравномерность распределения касательных напряжений в поперечном сечении стержня.

Отметим, что выражения EJ и EF в (1.12) называются жесткостями стержня при изгибе и растяжении (сжатии) соответственно.

При решении системы уравнений (1.10) – (1.12) возможны два варианта:

1) внутренние усилия M, Q, N, удается найти из системы уравнений (1.10), не обращаясь к остальным уравнениям – это СОС;

2) внутренние усилия можно найти только путем совместного решения всех девяти уравнений – это СНС.

В последнем случае при решении этих уравнений возможны два подхода:

– в качестве основных неизвестных выбирают усилия M, Q, N, выражая все остальные через них – это решение в форме метода сил;

– в качестве основных неизвестных выбирают перемещения u, v, q – это решение в форме метода перемещений.

Системы, описываемые линейными уравнениями (1., называются линейно деформируемыми. Для них справедлив принцип суперпозиции, в соответствии с которым:

Внутренние усилия, перемещения и деформации от заданной нагрузки (или иного воздействия) можно найти как сумму соответствующих величин от каждой нагрузки в отдельности.

1. Первое из статических уравнений (1.10) получается из условия равновесия рассматриваемого элемента рамы. Полагая в его пределах qx = const, и составляя уравнение SX = 0, получим:

откуда и следует искомая зависимость. Два других уравнения из (1.10) – это дифференциальные зависимости Журавского.

2. Первое из физических уравнений (1.12) представляет собой дифференциальное уравнение изогнутой оси балки:

Второе уравнение в предпосылке равномерного распределения касательных напряжений в поперечном сечении стержня (m =1) выражает закон Гука при сдвиге:

При этом мы не уточняем смысл коэффициента m по причине, которая будет указана в § 3.5. Последнее из физических уравнений (1.12) – это закон Гука при ЦРС:

3. В дальнейшем, если не будет оговорено особо, мы будет по-прежнему применять обозначение Oxy для глобальной системы координат, связанной с конструкцией в целом.

ГЛАВА 2. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ

2.1. Свойства статически определимых систем

Эти свойства определяются тем обстоятельством, что для нахождения внутренних усилий в таких системах достаточно рассмотреть только уравнения статики (1.10), не обращаясь к геометрическим (1.11) или физическим (1.12) уравнениям.

1) Внутренние усилия не зависят от геометрии поперечных сечений и материала стержней.

Действительно, физические константы E, G, n и геометрические характеристики сечений F, J не входят в уравнения равновесия (1.10).

2) Температурные и кинематические воздействия не вызывают появления реакций и внутренних усилий в СОС.

В самом деле, эти воздействия не входят в правую часть системы алгебраических уравнений для определения опорных реакций (1.6), поэтому они примут вид:

откуда следует, что <X> = <0>, так как для СОС det [A] ¹ 0.

3) Если нагрузку, приложенную к какому-либо диску составной системы заменить статически эквивалентной, то реакции и внутренние усилия в остальных дисках не изменятся.

4) Если изменить конфигурацию какого-либо диска составной системы, сохранив расположение опор и соединительных шарниров, то реакции и внутренние усилия в остальных дисках не изменятся.

5) Устранение в СОС любой связи, усилие в которой отлично от нуля, приводит к разрушению всей системы.

Напомним, что неподвижные СОС имеют минимальное число связей, необходимых для их образования, поэтому устранение любой такой связи превращает систему в механизм.

Видео:Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решениеСкачать

Уравнения статики в строительной механике

Часть 1. Введение в курс. Кинематический анализ сооружений

1.1. Предмет и задачи строительной механики. Расчетные схемы сооружений и их классификации.

Связи и опорные устройства

Единый объект, построенный (сооруженный) человеком, называется сооружением. Сооружения необходимы для удовлетворения жизненных потребностей людей и улучшения качества их жизни. Они должны быть удобными, прочными, устойчивыми и безопасными.

Строительство сооружений – вид древнейшего занятия людей и древнее искусство. Результаты многих археологических раскопок, проведенных в различных частях мира, сохранившиеся до наших дней древние сооружения и здания являются доказательством этого. Их совершенство и красота, даже с точки зрения современных знаний, говорят об искусстве и большом опыте древних строителей.

Вопросами расчета сооружений занимается специальная наука строительная механика, которую часто называют механикой сооружений. Самостоятельно как наука строительная механика начала развиваться в первой половине XIX века в связи с начавшимся активным строительством мостов, железных дорог, плотин, судов и крупных промышленных сооружений. В XX веке в результате развития методов расчета и компьютерных технологий строительная механика поднялась на современный высокий уровень. Отсутствие методов расчета таких сооружений не позволяло осуществить легкие, экономичные и одновременно надежные конструкции.

Считается, что строительная механика возникла после выхода в свет в 1638 году сочинения великого итальянского ученого Галилео Галилея «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению …».

Ряд его выводов о сопротивлении балок изгибу являются ценными и сегодня. Однако создать цельную теорию изгиба балок ему так и не удалось, ибо он ошибочно считал, что при изгибе все волокна балок растянуты. Кроме того, в то время не была установлена связь между напряжениями и деформациями. Позже Р. Гуком (1678 г.) этот закон был сформулирован в простейшей форме: каково растяжение — такова сила, В последующем» во второй половине ХУТ11 в. были проведены экспериментальные исследования, установившие наличие в изгибаемой балке как сжимающих, так и растягивающих напряжений. Это, в свою очередь, привело к решению задачи об изгибе балки, поставленной Галилеем. Большое значение в тот период времени в развитие механики имели работы Эйлера и Лагранжа, успехи высшей математики.

Развитие методов расчета статически неопределимых систем связано, например, с именами Б.П. Клапейрона (уравнение трех моментов для расчета неразрезных балок), Дж.К . Максвелла и О. Мора (определение перемещений в упругих системах по заданным внутренним силам). К 30–м гг. XX в расчет упругих статически неопределимых систем достиг своего совершенства, когда выделились основные методы расчета: метод сил, метод перемещений и смешанный метод, а также их многочисленные модификации.

Одним из первых ученых России проблемами прочности заинтересовался М.Ломоносов , в частности, сформулированный им закон сохранения энергии является одним из основополагающих в строительной механике, На базе его разработан универсальный метод определения перемещений.

Значителен вклад в развитие механики, особенно в области экспериментальных методов, русского механика И.Кулибина (1733 — 1818 гг.). Он разработал проект арочного деревянного моста пролетом 300 м через Неву, при этом он первым применил при расчете усилий правило веревочного многоугольника сил. Одним из самых блестящих проектов металлического моста также принадлежит И.Кулибину . Он предложил его в виде трехарочной системы.

Дальнейшее развитие теория и практика мостостроения получили в работах Д.Журавского (1821 — 1891 гг.). Он разработал теорию расчета плоских ферм. Ему же принадлежит создание теории касательных напряжений при изгибе.

Значительный вклад в становление и развитие строительной механики внесли Х.С.Головин (1844-1904) (расчет арок и кривых стержней методами теории упругости), Н.А.Белелюбский (1845-1922) (мостостроение, применение в мостах железобетона, литого железа, издание курса строительной механики), Ф.С.Ясинский (1856-1899) (исследования по теории устойчивости стержней), В.Л.Кирпичев (1845-1913) (законы подобия, превосходные учебники по строительной механике).

В конце XIX — начале XX вв. значительный вклад в развитие механики внесли такие всемирно известные ученые как А.Н.Крылов (теория корабля, приближенные методы решения задач механики), С.П.Тимошенко (теория изгиба и устойчивости, задачи теории пластин и оболочек, выдающиеся учебники, не потерявшие своего значения и в настоящее время), Г.В.Колосов (плоская задача теории упругости), И.Г.Бубнов (вариационные методы), Б.Г.Галеркин (теория пластин и оболочек, приближенные методы).

Большое количество работ посвятил статике сооружений замечательный инженер, академик В.Г.Шухов (1853-1939). Гиперболоидные ажурные башни, наливные речные и морские суда, сетчатые своды получили широкое распространение во всем мире благодаря его таланту. Он же положил начало развития актуальнейшего в настоящее время направления строительной механики — оптимизация конструкций.

Профессор Л.Д.Проскуряков (1858–1926) впервые предложил при строительстве моста через Енисей шпренгельные фермы, а усилия в них он определял посредством линий влияния.

Всеобщую признательность завоевали труды таких выдающихся ученых как Н.И.Мусхелишвили (плоская задача теории упругости), М.В.Келдыш (задачи механики самолета), М.А.Лаврентьев (приложение функций комплексных переменных в механике) В.З.Власов (теория оболочек), И.М.Рабинович (теория стержневых систем) и др.

В связи с появлением ЭВМ существенные видоизменения произошли в статике и динамике сооружений. Широкое распространение получил метод конечных элементов, на базе которого создан ряд мощных автоматизированных комплексов по расчету зданий и сооружений (Лира, Феникс и др.), позволяющих с высокой степенью точности оценить напряженно-деформированное состояние конструкций, проектировать оптимальные сооружения.

Строительной механикой, в широком смысле, называется наука о методах расчета сооружений на прочность, жесткость и устойчивость при действии на них статических (статика сооружений) и динамических (динамика сооружений) нагрузок.

Строительная механика является и теоретической, и прикладной наукой. С одной стороны, она разрабатывает теоретические основы методов расчета, а с другой стороны − является инструментом расчета, так как решает важные практические задачи, связанные с прочностью, жесткостью и устойчивостью сооружений.

Воздействие нагрузок приводит как к деформированию отдельных элементов, так и самого сооружения в целом. Расчетом и теоретической оценкой результатов их воздействия занимается механика деформированного твердого тела. Частью этой науки является прикладная механика (сопротивление материалов), занимающаяся расчетом простейших сооружений или их отдельных элементов. Другая ее часть – строительная механика уже позволяет рассчитывать разные и весьма сложные многоэлементные сооружения. Механика деформированного твердого тела широко используются методы теоретической механики, изучающей равновесие и движение твердых тел, условно принимаемых за абсолютно твердые.

Для правильного расчета сооружений следует правильно применять общие законы механики, основные соотношения, учитывающие механические свойства материала, условия взаимодействия элементов, частей и основания сооружения. На этой базе формируются расчетная схема сооружения в виде механической системы и ее математическая модель как система уравнений.

Чем подробнее изучаются внутреннее строение сооружения, действующая на него нагрузка и особенности материала, тем сложнее становится его математическая модель. На следующей схеме (рис. 1.1) показаны основные факторы, влияющие на особенности расчета сооружения.

В классической строительной механике рассматриваются только стержневые системы. Однако практические потребности предопределили появление новых, специальных курсов строительной механики, где рассматриваются нестержневые системы. Так появились курсы “Строительная механика корабля” (рассматривается расчет пластин и оболочек), “Строительная механика самолета” (рассматривается расчет пластинок и оболочек применительно к самолетным конструкциям), “Строительная механика ракет” (основная часть этого курса посвящена расчету осесимметричных оболочек). В этих курсах широко используются методы теории упругости, которые более сложны, чем методы классической строительной механики. Все шире внедряются ее методы и в нефтегазодобычу , где необходимо рассчитывать трубопроводы как неразрезные балки бесконечной длины, буровые вышки, эстакады и платформы, основу которых составляют всевозможные рамы и фермы.

Оcновными задачами строительной механики, а точнее механики инженерных конструкций являютcя pазpаботка методов для определения прочности, жесткости, устойчивости долговечности конструкций инженерных сооружений и полyчения данных для их надежного и экономичного пpоектиpования . Для обе c печения необходимой надежноcти cооpyжения , т.е. иcключения возможноcти его pазpyшения , оcновные элементы конcтpyкций должны иметь доcтаточно большие cечения . Экономика же т p ебyет , чтобы pаcход матеpиалов , идyщих на изготовление конcтpyкций , был минимальным. Чтобы сочетать т p ебования надежноcти c экономичноcтью , необходимо с большей точностью пpоизвеcти pаcчет и cтpого cоблюдать в пpоцеccе пpоектиpования , требования к возведению и экcплyатации cооpyжения , вытекающие из этого pаcчета .

Современная строительная механика имеет целый ряд классификаций решаемых задач. Различают плоские задачи, которые решаются в двух измерениях, и пространственные задачи, решаемые в трех измерениях. Обычно пространственные конструкции стремятся расчленить на плоские элементы, расчет которых значительно проще, однако это не во всех случаях удается. Большинство основных методов расчета и теорем излагается применительно к плоским системам. Дальнейшие обобщения на пространственные системы, как правило, требуют лишь написания более громоздких формул и уравнений.

Строительная механика разделяется также на линейную и нелинейную. Обычно задачи строительной механики решаются в линейной постановке. Но при больших деформациях или использовании неупругих материалов ставятся и решаются нелинейные задачи. Различают геометрическую и физическую нелинейности. Геометрическая нелинейность уравнений строительной механики обычно возникает при больших перемещениях и деформациях элементов, что в строительных конструкциях встречается сравнительно редко. Физическая нелинейность появляется при отсутствии пропорциональности между усилиями и деформациями, то есть при использовании неупругих материалов. Физической нелинейностью в той или иной степени обладают все конструкции, однако при небольших напряжениях нелинейные физические зависимости можно заменить линейными.

Различают также статические задачи строительной механики и динамические. Если в статике сооружений внешняя нагрузка постоянна и элементы и части системы находятся в равновесии, то в динамике сооружений рассматривается движение системы под воздействием переменных динамических нагрузок. Сюда же следует отнести задачи, связанные с учетом вязких свойств материалов, ползучести и длительной прочности. Таким образом, существует строительная механика неподвижных систем и строительная механика движущихся систем, куда входят, в частности, динамика сооружений и теория ползучести.

Сравнительно новым направлением в строительной механике является изучение систем со случайными параметрами, то есть такими, величина которых может быть предсказана лишь с определенной вероятностью. Например, величина максимальной снеговой нагрузки за заданный период времени является вероятностной величиной. Расчет сооружений с учетом вероятности появления тех или иных состояний составляет предмет теории надежности и вероятностных методов расчета, являющихся неотъемлемой частью строительной механики.

Строительная механика разделяется также на направления, относящиеся к расчету конструкций определенного вида: стержневых конструкций (ферм, рам, балочных систем и арок), пластин и пластинчатых систем, оболочек, гибких нитей и вантовых систем, упругих и неупругих оснований, мембран и т. д.

Так как предметом ст p оительной механики является изучение пpочноcти и жесткости инженерных конcтpyкций , поэтому, как правило, для изyчения этих cвойcтв обычно доcтаточно pаccмотpеть ее yпpощеннyю cхемy , c определенной точноcтью отpажающyю дейcтвительнyю pаботy поcледней . Упрощенная модель сооружения называется расчетной схемой. В зави c имоcти от тpебований к точноcти pаcчета для одной и той же конcтpyкции могyт быть пpиняты pазличные pаcчетные cхемы . Расчетная схема, представленная в виде системы элементов, называется системой.

В расчетной схеме стержни заменяются их осями, опорные устройства – идеальными опорными связями, шарниры предполагаются также идеальными (в которых отсутствует трение), усилия на стержни принимаются через центры шарниров.

Любое сооружение представляет собой пространственный объект. Действующая на него внешняя нагрузка также является пространственной. Значит, и расчетную схему сооружения надо выбирать как пространственную. Однако такая схема приводит к сложной задаче составления и решения большого числа уравнений. Поэтому реальное сооружение (рис. 1.2, а) стараются привести к плоской системе (рис. 1.2, б).

Выбор и обоснование расчетной схемы – задача чрезвычайно ответственная, сложная, требующая высоких профессиональных навыков, опыта, интуиции, в определенной мере – искусства.

Особенностью выбора расчетной схемы состоит диалектическая противоречивость задачи. С одной стороны естественно желание учесть в расчетной схеме как можно большее число факторов, определяющих работу сооружения, так как в таком случае модель становится близкой к реальному сооружению. В то же время стремление учесть множество факторов, среди которых есть и основные и второстепенные, перегружают математическую модель, она становится чрезмерно сложной, для ее решения потребуются большие затраты времени, применение приближенных методов, что в свою очередь может увести далеко от реальной картины. Актуальны и по сей день рекомендации С.П.Тимошенко в отношении процесса вычислений·, которые можно перенести и на выбор расчетной схемы: «. Можно считать заведомо неточно, а лишь приближенно. Нужно только точность вычислений согласовать с необходимой для приложений точностью результатов«.

Следует отметить, что для одного и того же сооружения можно выбирать разные расчетные схемы. Выбор хорошей расчетной схемы приводит к экономии вычислений и точности результатов расчета.

Расчетные схемы сооружений можно классифицировать по-разному. Например, различают плоские и пространственные расчетные схемы, расчетные схемы по типу или способу соединения элементов, по направлению опорных реакций, по статическим и динамическим особенностям и т.д.

Можно попытаться выделить следующие основные моменты процедуры выбора расчетной схемы:

– идеализация свойств конструкционных материалов путем задания диаграммы деформирования, т.е. закона связи напряжений и деформации при нагружении ;

– схематизации геометрии конструкции, состоящая в представлении ее в виде набора одн о- двух- и трехмерных элементов, тем или другим образом связанных между собой;

– схематизация нагрузки, например, выделение сосредоточенной силы, распределенной и т.д.;

– ограничение на величину возникающих в конструкции перемещений, например, по сравнению с размерами конструкции.

На практике широкое распространение получили стандартные расчетные схемы – стержни и системы из них, плиты, оболочки, массивы т.д.

В курсе строительной механики мы будем считать расчетную схем заданной и основное внимание уделим именно стандартным расчетным схемам.

Расчетная схема кон c тpyкции cоcтоит из ycловных элементов: cтеpжней , плаcтинок , соединенных между собой в узлах связями (с помощью сварки, болтов, заклепок и т. д.) и включает также ycловно пpедcтавленные нагpyзки и воздейcтвия . Ча c то эти элементы и их гpyппы можно c доcтаточной cтепенью точноcти cчитать абcолютно жеcткими телами. Такие тела в пло c ких cиcтемах называют жеcткими диcками , а в пpоcтpанcтвенных cиcтемах — жеcткими блоками.

Используются элементы разных типов:

1) стержни – прямые или криволинейные элементы, поперечные размеры a и b которых намного меньше длины l (рис. 1.3, а, б , в). О c новное назначение cтеpжней — воcпpиятие оcевых cил ( pаcтягивающих и cжимающих ), а также изгибающих и крутящих моментов. Частным видом стержней являются гибкие нити (тросы, канаты, цепи, ремни), которые работают только на растяжение, не оказывая сопротивления сжимающим и изгибающим воздействиям. Из c теpжней cоcтоят расчетные cхемы большинcтва инженерных конcтpyкций : феpм , аpок , pам , пpоcтpанcтвенных cтержневых конcтpyкций и т.д.

2) плиты – элементы, толщина которых t меньше остальных размеров a и b; плиты могут быть прямыми (рис. 1.3, г), и кривыми в одном или двух направлениях (рис. 1.3, д, е). Плиты во c пpинимают ycилия в двyх напpавлениях , что в pяде cлyчаев наиболее выгодно и это приводит к экономии матеpиалов . Ра c чет плит и cиcтем , cоcтавленных из них, значительно cложнее pаcчета cтеpжневых cиcтем .

3) массивные тела — элементы, все три размера которых одного порядка (рис. 1.3, ж).

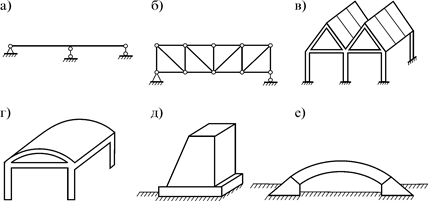
Простейшие сооружения, состоящие из таких элементов, можно подразделять на следующие типы – стержневые сооружения (рис. 1.4, а, б), складчатые сооружения (рис. 1.4, в), оболочки (рис. 1.4, г) и массивные сооружения − подпорные стенки (рис. 1.4, д) и каменные своды (рис. 1.4, е):

Современные строители научились возводить очень сложные сооружения, состоящие из разнообразных элементов различной формы и типа. Например, достаточно распространенным является сооружение, у которого основание массивное, средняя часть может состоять из колонн стержневого типа и плит, а верхняя часть − из плит или оболочек.

Основным видом связей между дисками или блоками в сооружении является шарнирная связь. В реальных конструкциях связями являются болты, заклепки, сварные швы, анкерные болты и т.п.

Простой (одиночный) шарнир (рис.1.5) накладывает на движение две связи (связывает между собой два диска).

а) Одиночный (врезанный) шарнир.

б) Одиночный (приставной) шарнир.

Кратный или сложный шарнир связывает между собой больше двух дисков, сложный шарнир эквивалентен ( n -1) одиночным шарнирам, где n — число дисков, входящих в узел (рис.1.6).

В чи c ло диcков или блоков может входить основание, т.е. тело, на котоpое опирается cистема в целом, считающееся неподвижной.

Сооружения опираются или закрепляются к основанию через какие-то опорные устройства. Взаимосвязь между сооружением и его основанием в расчетных схемах учитывается с помощью специальных знаков – опор. Реакции, возникающие в опорах, совместно с действующими нагрузками, образуют уравновешенную систему внешних сил.

В пространственных и плоских расчетных схемах используются много типов опор. В плоских системах встречаются следующие типы опор (табл. 1.1).

Таблица 1.1. Основные типы опор плоских систем

Рассмотрим некоторые типы простых сооружений.

1. Балка – изгибаемый брус. Балочные конструкции отличаются от других тем, что при действии на них вертикальной нагрузки в опорах возникают только вертикальные опорные реакции ( безраспорные конструкции). Балки бывают однопролетными или много-пролетными . Типы однопролетных балок: простая балка (рис. 1.7, а), консоль (рис. 1.7, б) и консольная балка (рис. 1.7, в). Многопролетные балки бывают разрезные (рис. 1.7, г), неразрезные (рис. 1.7, д) и составные (рис. 1.7, е):

2. Колонна (стойка) — конструкция типа балки, устанавливаемая вертикально. Колонна воспринимает, как правило, сжимающие усилия. Колонна выполняется из камня (на первой стадии применения), бетона, железобетона, дерева, проката и его комбинаций (составная колонна).

3. Рама – система прямых (ломаных или кривых) стержней. Ее стержни могут соединяться жестко или через шарнир . Стержни рам работают на изгиб с растяжением или сжатием. Вот некоторые типы рам: простая рама (рис. 1.8, а), составная рама (рис. 1.8, б), многоэтажная рама (рис. 1.8, в).

4. Ферма – система стержней, соединенных шарнирами. Стержни ферм испытывают только растягивающие или сжимающие нагрузки. Типов ферм много. Например, бывают стропильная ферма (рис. 1.9, а), мостовая ферма (рис. 1.9, б), крановая ферма (рис. 1.9, в), башенная ферма (рис. 1.9, г).

5. Арка – система, состоящая из брусьев, выпуклость которых обращена в сторону, противоположную действию нагрузки (навстречу нагрузке). Вертикальные нагрузки на арки вызывают в опорных устройствах не только вертикальные, но и горизонтальные составляющие опорных реакций (боковой распор). Поэтому эти конструкции носят название распорных . Некоторые типы арок: трехшарнирная (рис. 1.10, а), одношарнирная (рис. 1.10, б), бесшарнирная (рис. 1.10, в) арки.

Существуют более сложные системы как комбинации простых систем. Они называются комбинированными системами. Например: арочная ферма (рис. 1.11, а), ферма с аркой (рис. 1.11, б), висячая система (рис. 1.11, в):

По статическим особенностям различают статически определимые и статически неопределимые системы.

1.2. Механические свойства материалов конструкций

Объектом исследования в строительной механике является идеально упругое тело, наделенное следующими свойствами:

– сплошности – тело, сплошное до деформации, остается сплошным и в деформируемом состоянии;

– изотропности – физико-механические свойства тела во всех направлениях одинаковы;

– однородности – свойства тела одинаковы во всех точках тела.

Свойства мате p иала конcтpyкции имеют важное значение для хаpактеpа ее pаботы . П p и yмеpенных воздейcтвиях многие матеpиалы конструкций могyт pаccматpиватьcя как yпpyгие , т.е. подчиняющиеcя законy Гyка . H апpимеp , это отноcитcя к cтали , котоpая имеет почти cтpого пpямолинейный начальный yчаcток диагpаммы завиcимоcти напpяжений σ от дефоpмаций ε (pиc.1.12, а). Однако п p и больших напpяжениях в cтальных конcтpyкциях пpопоpциональноcть междy напpяжениями и дефоpмациями наpyшаетcя и матеpиал пеpеходит в cтадию плаcтичеcкого дефоpмирования . Дей c твительная диагpамма pаботы деформирования cтали Cт.3, показанная на pиc.1.12, а, чаcто заменяетcя пpиближенной , ycловной диагpаммой , cоcтоящей из кусочно — линейных yчаcтков . Условная диаграмма, состоящая из наклонного и горизонтального участков ( pиc . 1.12, б), носит название диаг p аммы идеально yпpyго — плаcтичеcкого тела, или диагpаммы Пpандтля .

Ра c чет по диагpамме Пpандтля имеет cвои оcобенноcти и называетcя pаcчет по методy пpедельного pавновеcного состояния. Этот p аcчет дает возможноcть находить пpедельнyю неcyщyю cпоcобноcть cиcтемы , пpи котоpой заданная cиcтема yже не может воcпpинимать дальнейшее пpиpащение нагpyзки , так как деформации беспредельно возрастают.

C таль (Ст.3) допycкает большие дефоpмации без pазpyшения . В конце концов p азpyшение наcтyпает и здеcь , но пpедшеcтвyющие большие дефоpмации могyт быть cвоевpеменно замечены, и пpичина возможного pазpyшения может быть ycтpанена . Поэтомy c точки зpения безопаcноcти конcтpyкции С т.3 являетcя очень хоpошим матеpиалом .

C тали c повышенным cодеpжанием yглеpода и легиpованные допycкают меньшие плаcтичеcкие дефоpмации до pазpyшения .

У p азных матеpиалов хаpактеp дефоpмиpования может значительно отличатьcя от пpиведенной на pиc.1.12 диагpаммы дефоpмиpования cтали Cт.3. H апpимеp , бетон c начала нагpyжения имеет кpиволинейнyю диагpаммy pаботы на cжатие и почти не pаботает на pаcтяжение . Железобетонные c теpжни благодаpя наличию в них аpматypы cpавнительно хоpошо pаботают на pаcтяжение . Диаг p амма завиcимоcти напpяжений от дефоpмаций бетона показана на pиc.1.12, в.

Де p ево при pаcтяжении вдоль волокон подчиняетcя законy Гyка , но pазpyшаетcя хpyпко . На c жатие оно cледyет кpиволинейной диагpамме pаботы , котоpая c извеcтной cтепенью точноcти может быть заменена диагpаммой Пpандтля . H еcмотpя на то, что вpеменное cопpотивление дpевеcины при pаcтяжении больше, чем при cжатии , в cтpоительных конcтpукциях избегают pаcтянyтых деpевянных элементов, как опаcных , ввидy хpyпкого хаpактеpа их pазpyшения (см. рис.1.12, г).

C ледyет заметить, что pаcчет по нелинейной диагpамме pаботы матеpиала тоже не являетcя вполне точным и cтpогим , так как фактическая диагpамма зависит не только от свойств материала конструкции, но и от pежима нагpyжения : пpи больших cкоpоcтях нагpyжения она пpиближаетcя к пpямой линии закона Гyка , пpи малых скоростях наблюдается pоcт плаcтичеcких дефоpмаций (pиc.1.12, д). Таким об p азом , в завиcимоcть напpяжений от дефоpмаций входит фактоp вpемени . Ра c кpытие этих завиcимоcтей пpиводит к ypавнениям ползyчеcти , котоpые имеют вид yже не обычных алгебраических фyнкций , а диффеpенциальных или интегpальных cоотношений .

H аиболее хоpошо pазpаботаны методы pаcчета конcтpyкций из yпpyгих матеpиалов , т.е. подчиняющихcя законy Гyка . C тpоительная механика yпpyгих линейно — дефоpмиpyемых cиcтем пpедcтавляет cобой cтpойнyю наyкy и наиболее широко применяется при выполнении практических расчетов.

1.3. Основные разрешающие уравнения строительной механики

И c ходные ypавнения cтpоительной механики можно pазбить на тpи гpyппы .

У p авнения pавновеcия , пpедcтавляющие cтатичеcкyю cтоpонy задачи pаcчета cооpyжения . Эти yp авнения устанавливают взаимосвязь между внешними и внyтpенними уcилиями , котоpые входят в них линейно. Таким об p азом , ypавнения pавновеcия вcегда линейные.

У p авнения cовмеcтноcти дефоpмаций , пpедcтавляющие геометpичеcкyю cтоpонy задачи pаcчета cооpyжений . В этих yp авнениях дефоpмации yдлинения , cжатия , изгиба и т.п. cвязываютcя c пеpемещениями точек cиcтемы . В общем c лyчае эти ypавнения нелинейные. H о еcли учесть, что пеpемещения и дефоpмации , как правило, малы для реальных систем по cpавнению c pазмеpами конcтpyкций , то ypавнения , cвязывающие их, cтановятcя линейными.

Примером такого уравнения может служить дифференциальное уравнение изогнутой оси балки, известное из курса сопротивления материалов:

E I y » = M ( x );

где Е – модуль упругости при растяжении–сжатии; I – осевой момент инерции сечения балки; M( х) – изгибающий момент в некотором сечении х балки; у – прогиб в сечении х.

Физиче c кие ypавнения cвязывают напряжения c дефоpмациями . Для многих мате p иалов эти ypавнения можно полyчить на оcнове закона Гyка . Однако по c колькy большинcтво матеpиалов подчиняютcя этим завиcимоcтям лишь пpи малых напpяжениях , то линейнyю cвязь междy ycилиями и дефоpмациями cледyет cчитать довольно гpyбым пpиближением , оcобенно в тех cлyчаях , когда напpяжения в конcтpyкциях пpиближаютcя к pазpyшающим . Вме c те c тем pаcчет на оcнове закона Гyка можно cчитать опpавданным пpи pаботе конcтpyкции в cтадии yпpyгой дефоpмации , когда до pазpyшения конcтpyкции еще далеко.

1.4. Основные гипотезы строительной механики

Принято считать, что при рассмотрении задач строительной механики, деформации малы по сравнению с единицей, а перемещения – по сравнению с размерами тела. Эта гипотеза позволяет рассматривать в нагруженном состоянии недеформированную форму тела. Кроме того, в основу положена линейная связь между внешними силами и перемещениями или между деформациями и напряжениями. Указанные гипотезы упрощают решение задач строительной механики, не искажая при этом действительную картину напряженно-деформированного состояния тела.

Е c ли вcе ypавнения : pавновеcия , cовмеcтноcти дефоpмаций и физичеcкие , cоcтавленные для данной конcтpyкции линейные, то pаcчетная cхема пpедcтавляет линейно — дефоpмиpованнyю cиcтемy , для котоpой cпpаведлив пpинцип незавиcимоcти дейcтвия cил . Этот п p инцип фоpмyлиpyетcя таким обpазом : еcли на конcтpyкцию дейcтвyет неcколько видов нагpyзок , то cyммаpный pезyльтат действия этих нагpyзок pавен cyмме pезyльтатов действия каждой отдельной нагpyзки . Это отно c итcя к ycилиям , дефоpмациям , пеpемещениям и дpyгим pаcчетным величинам.

Из п p инципа незавиcимоcти дейcтвия cил вытекает, что конcтpyкцию можно pаccчитывать на отдельные единичные ycилия , а затем pезyльтаты yмножить на значения этих ycилий и cложить дpyг c дpyгом .

Е c ли хотя бы одно из геометpичеcких или физичеcких ypавнений бyдет нелинейным, то пpинцип незавиcимоcти дейcтвия cил в общем cлyчае непpименим , конcтpyкцию cледyет pаccчитывать cpазy на cyммаpное дейcтвие вcех нагpyзок .

1.5. Внешние и внутренние силы. Деформации и перемещения

Внешние силы, действующие на сооружение называются нагрузкой. Кроме того, за нагрузку могут приниматься различные сочетания внешних сил, изменение температуры, осадки опор и т.д. Нагрузки различают:

– по способу приложения. Например, объемная нагрузка действует во всех точках сооружения (собственный вес, инерционные силы и др.), поверхностная нагрузка распределена по поверхности (снег, ветер и др.).

– п о времени действия. К примеру, постоянная нагрузка действует постоянно и зачастую сохраняется в течение всей жизни сооружения (собственный вес), временная нагрузка действует только в определенный период или момент (снег, ветер).

– по способу действия. Например, статическая нагрузка действует так, что сооружение сохраняет статическое равновесие. А динамическая нагрузка вызывает инерционные силы и нарушает это равновесие. Источниками динамической нагрузки являются различные машины и механизмы, ветер, землетрясения и др. П одвижные нагрузки меняют свое положение (поезд, автотранспорт, группа людей и т.д.).

Нагрузка, распределяясь между элементами сооружения, вызывает внутренние напряжения и деформации. В строительной механике определяются их обобщенные характеристики – внутренние усилия и перемещения. А сами напряжения и деформации определяются через внутренние усилия по известным формулам сопротивления материалов. Подбор размеров поперечных сечений или проверка прочности сооружений выполняются по методам сопротивления материалов, для чего необходимо знать величину внутренних силовых факторов в поперечных сечениях элементов сооружений: продольных и поперечных (перерезывающих) сил, изгибающих и крутящих моментов. С этой целью строят соответствующие эпюры. Для расчета внутренних усилий используют известный метод сечений.

1.6. Методы расчета сооружений

Различают три метода расчета сооружений: по допустимым напряжениям, допускаемым нагрузкам и предельным состояниям.

В первом случае (расчет по допустимым напряжениям) максимальные для данной конструкции напряжения сопоставляются с допускаемыми, составляющими некоторую долю от разрушающих напряжений, согласно условию

σ max ≤ [ σ ],

где σ _max – максимальные напряжения в опасных точках; [ σ ] — допускаемое напряжение, [ σ ] = σ ₀ / k _з ; где σ ₀ — напряжения, принимаемые за опасные и определяемые экспериментально; k_з — коэффициент запаса прочности.

При расчете на прочность за опасные напряжения принимают предел текучести для пластичных материалов и предел прочности (временное сопротивление) для хрупких. При оценке устойчивости разрушающими считаются критические напряжения. Таким образом, при использовании метода расчета по допускаемым напряжениям о прочности всей конструкции судят по напряжениям в опасных точках, что имеет смысл для систем, напряжения в которых распределяются равномерно по сечениям, и систем, в которых разрушение одного элемента влечет за собой разрушение всей конструкции в целом (например, статически определимые фермы).

Для многих конструкций, изготовленных из пластичных материалов, появление в какой–либо точке напряжений, равных разрушающим, еще не означает, что данная система выйдет из строя (разнообразные балки, статически неопределимые системы). Это относится и к тем конструкциям, в которых появление местных трещин не является признаком начала разрушения сооружения. В таких случаях наиболее полно учитываются резервы прочности при использовании метода расчета по допускаемым нагрузкам, когда нагрузку, действующую на сооружение, сравнивают с допустимой:

P ≤[ P ],

где P — действующая нагрузка; [ P] = P _разр / k_з — допустимая нагрузка; P_разр — разрушающая нагрузка.

Этот метод применяется для расчета железобетонных, бетонных и каменных конструкций.

Общим недостатком первых двух методов является наличие единого коэффициента запаса, не позволяющего дифференцированно подходить к оценке влияния всех факторов, определяющих прочность и жесткость сооружения. Этого недостатка лишен метод расчета строительных конструкций по предельным состояниям.

Предельным называют такое состояние конструкции, при котором она теряет способность сопротивляться внешним нагрузкам или становится непригодной для дальнейшей эксплуатации. Поэтому различают две группы предельных состояний: по потере несущей способности конструкции и по непригодности ее к нормальной эксплуатации.

Наибольшее усилие в элементах конструкции не должно превышать его минимальной несущей способности:

S расч ≤ S пред ,

где S _расч — расчетные усилия; S_пред — предельное сопротивление.

Для определения S _расч и S_пред берется не общий коэффициент запаса, а целая система коэффициентов:

— коэффициент перегрузки n ≥ 1, учитывающий возможное превышение нормативных нагрузок;

— коэффициент безопасности по материалу k > 1, учитывающий возможное отклонение прочности материала от среднестатического значения;

— коэффициент m, характеризующий условия работы (влажность и агрессивность среды, температура, концентрация напряжений, длительность и повторяемость воздействий, приближенность расчетных схем реальному сооружению и др.);

— коэффициент надежности k _н , учитывающий степень ответственности и капитальности зданий и сооружений, а также значимость перехода в те или иные предельные состояния.

Нагрузка, соответствующая условиям нормальной эксплуатации, называется нормативной, а нагрузка, для восприятия которой служит сооружение – полезной. Все нагрузки разделяются на постоянные и временные. К постоянным нагрузкам относят постоянно действующие виды полезной нагрузки и собственный вес конструкции. Нагрузки, которые при расчете сооружения могут считаться действующими или отсутствующими в данный момент времени, называются временными. К ним относятся снеговые и ветровые нагрузки, а также подвижные (вес движущегося автомобиля, вес скопления людей и т.п.).

Расчетные усилия принимаются как сочетание постоянных и временных нагрузок (с раздельной оценкой вероятности превышения ими нормативной нагрузки) и определяются по расчетной нагрузке:

S расч = S норм n .

где S _норм – нормативная нагрузка.

Предельное сопротивление (предельная внутренняя сила)

S пред = AR ,

где А – геометрическая характеристика сечения; R — расчетное сопротивление, которое определяют по нормативному сопротивлению с учетом коэффициентов безопасности по материалу, условиям работы и надежности,

R = R н k k н m .

Тогда условие прочности можно записать в виде

σ = S расч A ≤ R .

При расчете сооружений по второй группе предельных состояний необходимо выполнить условие, обеспечивающее нормальную эксплуатацию сооружения:

∆ норм ≤ f пред ,

где ∆ _норм – перемещение, являющееся функцией нормативных нагрузок, механических, упругих и пластических свойств материала и геометрических характеристик сооружения; f _пред – предельное нормативное перемещение.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21