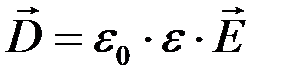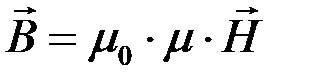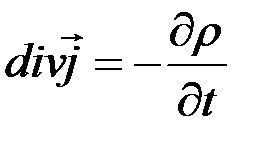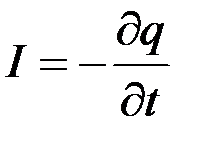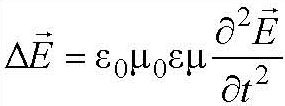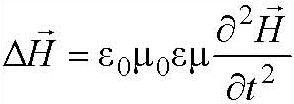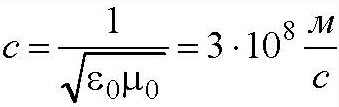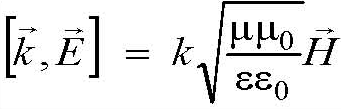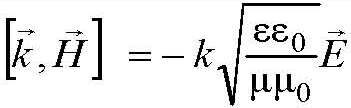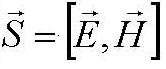Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать
Материальные уравнения
Пусть имеем однородную и изотропную среду, для которой известны диэлектрическая проницаемость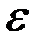 
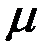
и магнитная проницаемость 
. Эти величины связаны со строением и поведением атомов и молекул среды. Для вакуума эти величины равны единице.
Пятое уравнение Максвеллаустанавливает связь между вектором напряженности электрического поля и вектором электрической индукции. Оно имеет вид:
В эту формулу входит величина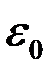 
, которая называется электростатической постоянной вакуума. Это фундаментальная константа, которая определяет скорость распространения электромагнитных волн в вакууме.
Шестое уравнение Максвеллаустанавливает связь между вектором напряженности магнитного поля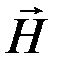 
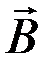
и вектором индукции магнитного поля 
. Оно имеет вид:
Пятое и шестое уравнения Максвелла позволяют рассчитывать характеристики электрического и магнитного полей в некоторой среде, а не только в вакууме. Кроме того, эти уравнения содержат информацию о распространении электромагнитного поля.
Седьмое уравнение Максвелла представляет собой закон сохранения электрического заряда, который может быть записан в различных формулировках.
В дифференциальной форме
Закон сохранения электрического заряда в интегральной форме записывается следующей формулой:
или 
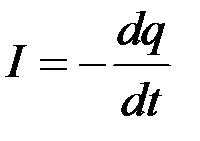
Электромагнитная волна— процесс распространения в пространстве возмущения электромагнитного поля.
Существование электромагнитных волн является следствием уравнений Максвелла.
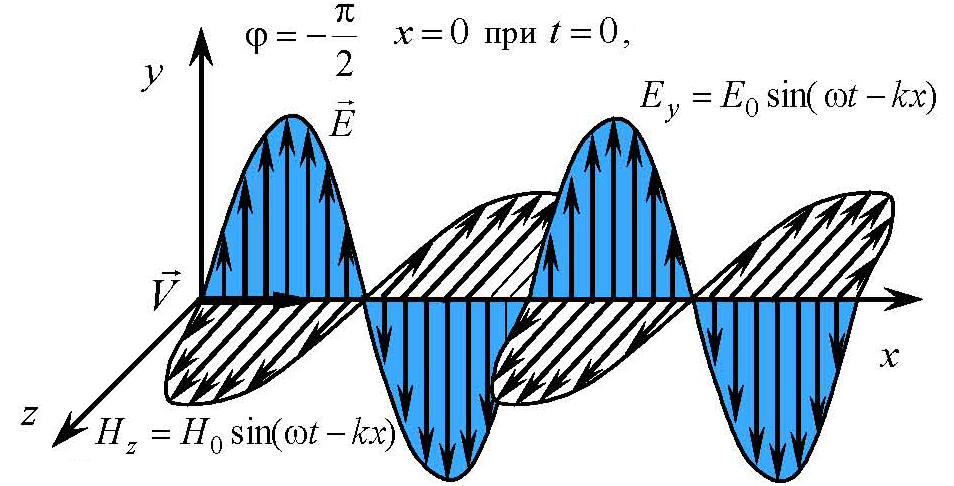
Это значит, что напряженности Е и Н переменного электромагнитного поля в однородной, изотропной, непроводящей, нейтральной среде должны удовлетворять волновому уравнению, то есть переменное электромагнитное поле будет распространяться в пространстве в виде волны.
Сравнивая полученные уравнения с волновым уравнением, записанным в общем виде получим, что
, где 
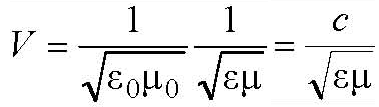
Из уравнений Максвелла следует также, что в однородной и изотропной среде
Векторы Е и Н вместе с волновым вектором k образуют правую тройку векторов
Электромагнитные волны, как любые волны, не переносят вещество — это распространяющиеся электрические и магнитные поля, они переносят электромагнитную энергию. Для характеристики переноса энергии используют векторное произведение напряженностеи электрического и магнитного поля — вектор Пойнтинга(J. Poynting, 1852-1941), введенный Джоном Пойнтингом в 1884 году
По определению интенсивности волны она равна среднему значению модуля вектора Пойнтинга, при этом усреднение должно проводиться или за целое число периодов или за время, много большее периода колебаний.
Видео:Уравнение состояния идеального газа. 10 класс.Скачать
максвелла уравнения
МАКСВЕЛЛА УРАВНЕНИЯ
1. Краткая история
2. Каноническая форма
3. Максвелла уравнения в интегральной форме
4. Общая характеристика Максвелла уравнений
5. Максвелла уравнения для комплексных амплитуд
6. Алгебраические Максвелла уравнения
7. Материальные уравнения
8. Граничные условия
9. Двойственная симметрия Максвелла уравнений
10. Максвелла уравнения в четырёхмерном представлении
11. Лоренц-инвариантность Максвелла уравнений
12. Лагранжиан для электромагнитного поля
13. Единственность решений Максвелла уравнений
14. Классификация приближений Максвелла уравнений
15. Максвелла уравнения в различных системах единиц
Максвелла уравнения — ур-ния, к-рым подчиняется (в пределах применимости классической ыакроскопич. электродинамики, см. Электродинамика классическая), электромагнитное поле в вакууме и сплошных средах.
1. Краткая история
Установлению M. у. предшествовал ряд открытий законов взаимодействий заряженных, намагниченных и токонесущих тел (в частности, законов Кулона, Био — Савара, Ампера). В 1831 M. Фарадей (M. Faraday) открыл закон эл—магн. индукции и примерно в то же время ввёл понятие электрич. и магн. полей как самостоят, физ. субстанций. Опираясь на фарадеевское представление о поле и введя ток смещения, равнозначный по своему магн. действию обычному электрич. току, Дж. К. Максвелл (J. С. Maxwell, 1864) сформулировал систему ур-ний, названную впоследствии ур-ниями Максвелла. M. у. функционально связывают электрич. и магн. поля с зарядами и токами и охватывают собой все известные закономерности макроэлектромагнетизма. Впервые о M. у. было доложено на заседании Лондонского Королевского общества 27 окт. 18(34. Первоначально Максвелл прибегал к вспомогат. механич. моделям «эфира», но уже в «Трактате об электричестве и магнетизме» (1873) эл—магн. поле рассматривалось как самостоят, физ. объект. Физ. основа M. у.- принцип близкодействия, утверждающий, что передача эл—магн. возмущений от точки к точке происходит с конечной скоростью (в вакууме со скоростью света с). Он противопоставлялся ньютоновскому принципу дальнодействия, сводящемуся к мгновенной передаче воздействий на любое расстояние 
Матем. аппаратом теории Максвелла послужил векторный анализ, представленный в инвариантной форме через кватернионы Гамильтона. Сам Максвелл считал, что его заслуга состоит лишь в матем. оформлении идей Фарадея.
2. Каноническая форма
Канонич. форма записи, принятая ныне, принадлежит Г. Герцу (H. Hertz) и О. Хевисайду (О. Heaviside) и основана на использовании не кватернионных, а векторных полей: напряжённости электрического поля E, напряжённости магнитного поля H, векторов электрической индукции D и магнитной индукции В. M. у. связывают их между собой, с плотностью электрического заряда
и плотностью электрического тока J, к-рые рассматриваются как источники:
Здесь использована Гаусса система единиц (о записи M. у. в др. системах см. в разделе 15). Входящие в (1) — (4) величины E, D, j являются истинными, или полярными, векторами (а величина r — истинным скаляром), поля H к В — псевдовекторами, или аксиальными векторами. Все эти величины предполагаются непрерывными (вместе со всеми производными) ф-циями времени t и координат 
Следовательно, в ур-ниях (1) — (4) не учитывается ни дискретная структура электрич. зарядов и токов, ни квантовый характер самих полей. Учёт дискретности истинных источников может быть произведён даже в доквантовом (классич.) приближении с помощью Лоренца — Максвелла уравнений.
3. Максвелла уравнения в интегральной форме
Используя Гаусса — Остроградского формулу и С такса формулу, ур-ниям (1) — (4) можно придать форму интегральных:
Криволинейные интегралы в (1a), (2a) берутся по произвольному замкнутому контуру (их наз. циркуляция-ми векторных полей), а стоящие в правых частях поверхностные интегралы — по поверхностям, ограниченным этими контурами (опирающимся на них), причём направление циркуляции (направление элемента контура
) связано с направлением нормали к S (вектор
) правовинтовым соотношением (если в качестве исходного выбрано пространство с правыми системами координат). В интегралах по замкнутым поверхностям (S) в (3а), (4а) направление вектора элемента площади 
совпадает с наружной нормалью к поверхности; V — объём, ограниченный замкнутой поверхностью S.
M. у. в форме (1a) — (4a) предназначаются не только для изучения топологич. свойств эл—магн. полей, но и являются удобным аппаратом решения конкретных задач электродинамики в системах с достаточно высокой симметрией или с априорно известными распределениями полей. Кроме того, в матем. отношении эта система ур-ний содержательнее системы (1) — (4), поскольку пригодна для описания разрывных, нодиффе-ренцируемых распределений полей. Но в отношении физ. пределов применимости обе системы ур-ний равнозначны, т. к. любые скачки полей в макроэлектродинамике должны рассматриваться как пределы микромасштабно плавных переходов, с тем чтобы внутри них сохранялась возможность усреднения ур-ний Лоренца — Максвелла. С этими оговорками резкие скачки можно описывать и в рамках M. у. (1) — (4), прибегая к аппарату обобщённых функций.
Наконец, M. у. в интегральной форме облегчают физ. интерпретацию MH. эл—магн. явлений и поэтому нагляднее сопоставляются с теми экспериментально установленными законами, к-рым они обязаны своим происхождением. Так, ур-ние (1a) есть обобщение Био — Савара закона (с добавлением к току 
максвелловского смещения тока).
Ур-ние (2a) выражает закон индукции Фарадея; иногда его правую часть переобозначают через «магн. ток смещения»
где
— плотность «магн. тока смещения», Ф В — магн. поток. Ур-ние (За) связывают с именем Гаусса 
, установившим соленоидальность поля В, обусловленную отсутствием истинных магн. зарядов. Впрочем вопрос о существовании магнитных монополей пока остаётся открытым. Но соответствующее обобщение M. у. произведено (Хевисайд, 1885) на основе принципа двойственной симметрии M. у. (см. в разделе 9), для чего в (2) и (2a) наряду с магн. током смещения вводится ещё и «истинный» магн. ток (процедура, обратная проделанной когда-то Максвеллом с электрич. током в первом ур-нии), а в ур-ние Гаусса (3), (За) — магн. заряд
где 
— плотность магн. заряда. Фактически все экспериментальные установки для регистрации ожидаемых магнитных монополей основаны на этом предположении. Наконец, ур-ние (4a) определяет поле свободного электрич. заряда; его иногда называют законом Кулона (Ch. A. Coulomb), хотя, строго говоря, оно не содержит утверждения о силе взаимодействия между зарядами, да и к тому же справедливо не только в электростатике, но и для систем с произвольным изменением поля во времени. На тех же основаниях иногда и ур-нпе (Ia) связывают с именем Ампера (A. Ampere).
4. Общая характеристика Максвелла уравнений
Совокупность M. у. (1) — (4) составляет систему из восьми (двух векторных и двух скалярных) линейных дифференц. ур-ний 1-го порядка для четырёх векторов 
Источники (скаляр
и вектор
) не могут быть заданы произвольно; применяя операцию 
к ур-нию (1) и подставляя результат в (4), получаем:
или в интегральной форме:
Это ур-ние непрерывности для тока, содержащее в себе закон сохранения заряда для замкнутых изолнров. областей
,- один из фундам. физ. принципов, подтверждаемых в любых экспериментах.
Ур-ния (1) — (4) распадаются на два самостоят, «блока»: ур-ния (1) и (4), содержащие векторы 
и источники 
и ур-ния (2) и (3) — однородные ур-ния для 
не содержащие источников. Ур-ння (2) и (3) допускают получение общего решения, в к-ром
выражаются через т. H. потенциалы электромагнитного поля
При этом ур-ние (3) «почти следует» из (2), т. к. операция (у), применённая к (2), даёт 
что отличается от (3) только константой, определяемой нач. условиями. Аналогично ур-ние (4) «почти следует» из (1) и ур-ния непрерывности (5).
Система M. у. (1) — (4) не является полной: по существу, она связывает 4 векторные величины двумя векторными ур-ниями. Её замыкание осуществляется путём добавления соотношений, связывающих векторы 1-го «блока»
с векторами 2-го «блока» 
Эти соотношения зависят от свойств сред (материальных сред), в к-рых происходят эл—магн. процессы, и наз. материальными ур-ниями (см. раздел 7).
5. Максвелла уравнения для комплексных амплитуд
В силу линейности системы (1) — (4) для её решений справедлив суперпозиции принцип .Часто оказывается удобным фурье-представление общего решения (1) — (4) как ф-ции времени (см. Фурье преобразование). Записывая временной фактор в виде 
, для комплексных фурье-амплитуд
и т. д.) получаем систему ур-ний
Система (1б) — (4б) в нек-ром смысле удобнее (1) — (4), ибо упрощает применение к эл—динамич. системам, обладающим временной дисперсией (см. раздел 7), т. е. зависимостью параметров от частоты
6. Алгебраические Максвелла уравнения
Если распространить (в силу линейности M. у.) фурье-разложение и на зависимость полей от пространственных координат, т. е. представить общее решение ур-ний (1) — (4) в виде суперпозиции плоских волн типа 
(k — волновой вектор), то для фурье-компонентов нолей
k и т. д.) получим систему алгебраич. ур-ний:
Такое сведение M. у. к набору ур-ний для осцилляторов (осцилляторов поля) составляет важный этап перехода к квантовой электродинамике, где эл—магн. поле рассматривается как совокупность фотонов, характеризуемых энергиями 
и импульсами 
Однако и в макроэлектродинамике представления (1в) — (4в) оказываются иногда вполне адекватными физ. сущности процессов: напр., при выделении откликов высокодобротных систем (см. Объёмный резонатор) или при изучении «механизма формирования» мод со сложной пространственной структурой из набора плоских волн и т. п. Наконец, M. у. в форме (1в) — (4в) удобны для описания свойств эл—динамич. систем, обладающих не только временной, но и пространственной дисперсией, если последняя задаётся в виде зависимости параметров от волнового вектора k.
7. Материальные уравнения
В макроэлектродинамике материальные связи, характеризующие эл—магн. свойства сред, вводятся феноменологически; они находятся либо непосредственно из эксперимента, либо на основании модельных представлений. Существуют два способа описания: в одном векторы E и H считаются исходными и материальные ур-ния задаются в виде D = D(E , H) и В = В( Е,Н), в другом — за исходные берутся векторы 2-го «блока» E и В, и соответствующие материальные связи представляются иначе: D = D(E,В), H= H(E, В). Оба описания совпадают для вакуума, где материальные уравнения вырождаются в равенства D = E и B = H.
Рассмотрим простейшую модель среды, характеризуемую мгновенным, локальным поляризац. откликом на появляющиеся в ней поля E и H. Под действием поля E в такой среде возникает электрич. поляризация 
(см. Поляризации вектор), а под действием поля H — магн. поляризация 
. Чаще её наз. намагниченностью и обозначают М.
Материальные ур-ния для таких сред имеют вид
При этом индуцированные в среде электрич. заряды наз. связанными или поляризац. зарядами с плотностью 
, а токи, обусловленные их изменениями,- поляризац. токами с плотностью
:
Эти понятия были перенесены и на магн. поля, что можно выразить в виде системы ур-ний, аналогичной
и только потом выяснилось, что истинными источниками намагничивания среды оказались электрич. токи 
, а не магн. заряды. Поэтому терминология сложилась на основе физически некорректной системы
тогда как следовало бы принять беззарядовые ур-ния
что равносильно замыканию исходных M. у. (1) — (4) с помощью материальных связей
Из (6) и (7a) следует, что 2-й вариант представления материальных соотношений, в к-ром постулируются в качестве исходных векторы E и B, физически предпочтительнее.
В модели Лоренца — Максвелла усреднение микрополя Нмикро, произведённое с учётом вклада со стороны индуциров. полей, приводит к ур-ниям (9) и соответственно = В. Однако обычно параметры сред вводятся с помощью ур-ний (7), что облегчает двойственную симметризацию ф-л (подробнее см. в разделе 9). Напр., скалярные восприимчивости сред (c e , c m ) определяются соотношениями
Простейшие модели сред характеризуются пост, значениями
В случае вакуума
0.
Классификация разл. сред ооычно основывается на материальных ур-ниях типа (10) и их обобщениях. Если проницаемости e и m не зависят от полей, то M. у. (1) — (4) вместе с материальными ур-ниями (10) остаются линейными, поэтому о таких средах говорят как о линейных средах. При наличии зависимостей
среды наз. нелинейными: решения M. у. в нелинейных средах не удовлетворяют принципу суперпозиции. Если проницаемости зависят от координат 
то говорят о неоднородных средах, при зависимости от времени 
— о нестац попарных средах (иногда такие эл—динамич. системы наз. параметрическими). Для анизотропных сред скаляры e, m в (10) заменяются на тензоры: 
(по дважды встречающимся индексам производится суммирование). Важное значение имеют также эффекты запаздывания и нелокальности отклика среды на внеш. поля.
Значение индуциров. поляризации Р е , напр, в момент г, может определяться, вообще говоря, значениями полей во все предыдущие моменты времени, т. е.
что при преобразовании Фурье по времени приводит к зависимости 
[соответственно
i]. Такие среды наз. средами с временной (частотной) дисперсией или просто диспергирующими средами. Аналогичная связь устанавливается и для нелокальных взаимодействий, когда отклик в точке г зависит от значения полей, строго говоря, во всех окружающих точках
но обычно всё-таки в пределах нек-рой конечной её окрестности: 
При преобразовании Фурье по г это приводит к появлению зависимостей 
такие среды наз. средами с пространственной дисперсией (см. Дисперсия пространственная).
В проводящих средах входящая в M. у. (1) — (5) плотность тока 
состоит из двух слагаемых: одно по-прежнему является сторонним током
обусловленным заданным перемещением электрич. зарядов под действием сторонних сил (обычно неэлектрич. происхождения), а другое — током проводимости
зависящим от полей, определяемых системой M. у., и связанным с ними материальными ур-ниями вида 
В простейшем случае эта зависимость сводится к локальному Ома закону,
где 
— электропроводность (проводимость) среды. Иногда в (11) вводят обозначение
, благодаря к-рому различают системы с заданными токами и системы с заданными полями (напряжениями). Для синусоидальных во времени полей, подчинённых ур-ниям (1б) — (4б) и материальным связям (10) и (11), вводится комплексная диэлектрич. проницаемость, объединяющая (10) и (11),
, мнимая часть к-рой обусловлена проводимостью и определяет диссипацию энергии эл—магн. поля в среде. По аналогии вводится комплексная магн. проницаемость
, мнимая часть к-рой обусловливает потери, связанные с перемагничиванием среды. Комплексные проницаемости в общем случае зависят от частоты w и волнового вектора
эти зависимости не могут быть произвольными: причинности принцип связывает их действительные и мнимые части Крамерса — Кронига соотношениями.
В общем случае вид материальных ур-ний зависит также и от системы отсчёта, в к-рой эти ур-ния рассматривают. Так, если в неподвижной системе К среда характеризуется простейшими ур-ниями (10), то в инер-циальной системе К’ , движущейся относительно К с пост, скоростью и, появляется анизотропия:
где индексы
обозначают продольные и поперечные к
составляющие векторов. В рамках алгебраич. M. у. (1в) — (4в) материальные ур-ния (12) могут быть переписаны в виде
что можно трактовать как наличие временной и пространственной дисперсии. Исследование процессов с материальными связями типа (12) составляет предмет электродинамики движущихся сред. Заметим, что хотя характеристики е и m удобно симметризуют материальные ур-ния, их введение не является непременным условием замыкания M. у. Соответствующей перенормировкой допустимо свести описание магн. поля к одно-векторному, т. е. сделать 
но при этом даже для изотропной среды диэлектрич. проницаемость становится тензором, она различна для вихревых и потенциальных полей. Физически это связано с неоднозначностью модельного представления диполь-ных моментов, во всяком случае при
они могут равноправно интерпретироваться и как зарядовые, и как токовые.
8. Граничные условия
Поскольку M. у. справедливы для любых (в рамках применимости макроэлектродинамики) неоднородных сред, то в областях резкого изменения их параметров иногда можно игнорировать тонкую структуру распределения полей в переходном слое и ограничиться «сшиванием» полей по разные стороны от него, заменяя тем самым переходный слой матем. поверхностью — границей, лишённой толщины. Если внутри переходной области имелись заряды с объёмной плотностью
или токи с объёмной плотностью
то при сжатии слоя в поверхность сохраняются их интегральные значения ·- вводятся поверхностные заряды r пов и поверхностные токи
— толщина переходного слоя.
Применение M. у. и ур-ния непрерывности приводит к следующим граничным условиям:
Здесь индексы 1 и 2 характеризуют поля по разные стороны от границы, а
— единичный вектор нормали к поверхности, направленный из среды 1 в среду 2. Правила (1г) — (5г) пригодны для перехода через любые поверхности, независимо от того, совпадают ли они с границами раздела сред или проходят по однородным областям, поэтому их иногда наз. поверхностными M. у.
Иногда граничные условия (1г) — (5г) порождают краевые условия, т. е. задают не правила перехода через границу, а сами поля на ней. Напр., внутри идеального проводника 
в силу (11) 
(иначе возник бы ток неограниченной плотности), поэтому на границе раздела диэлектрик — идеальный проводник в согласии с (2г)
Такие границы наз. идеальными электрич. стенками. Аналогично вводится понятие идеальной магн. стенки, на к-рой 
Если структура полей по одну сторону от границы универсальна, т. е. не зависит от распределения полей по др. сторону, то краевые условия могут состоять в задании не самих полей, а лишь связей между ними, напр. 
где Z — нек-рая скалярная или тензорная ф-ция координат границы (
— тангенциальный компонент
). К условиям такого рода относится, в частности, Леонтовича граничное условие для синусоидально меняющихся во времени полей на поверхности хороших проводников.
9. Двойственная симметрия Максвелла уравнений
Двойственная симметрия M. у. имеет место для любой формы их записи. Она состоит в инвариантности M. у. относительно линейных преобразований нолей, производимых по след, правилам:
Здесь
— произвольный угл. параметр; в частности, при
= О получаются тождественные преобразования, а при 
— стандартные преобразования перестановочной двойственности (операция 
): замена 
даёт в областях, свободных от источников, новое решение M. у. При этом, однако, оно меняет местами ур-ния
и, следовательно, там, где раньше были распределены электрич. источники, возникают источники магнитные
. Поэтому с точки зрения двойственной симметрии M. у. задание материальных связей в виде 
представляется вполне удобным. Дуально-симметричные M. у. обладают рядом достоинств, по крайней мере в чисто методич. плане. Так, напр., они симметризуют скачки тангенциальных компонентов магн. и электрич. полей и, если задание ff Tall на поверхности идеальной электрич. стенки эквивалентно заданию поверхностного электрич. тока, то задание Я 1а „ на идеальной магн. стенке сводится к заданию магн. поверхностного тока:
Таким сведением задач с заданными
полями к задачам с заданными токами широко пользуются в теории дифракции волн, в частности в дифракции радиоволн.
Принцип перестановочной двойственности является представителем класса дискретных преобразований (см. Симметрия ),оставляющих инвариантными M. у. Такого же сорта преобразованиями являются, в частности, операция обращения времени
последовательно осуществляемые комбинации операций 
10. Максвелла уравнения в четырёхмерном представлении
Придавая времени t смысл четвёртой координаты и представляя её чисто мнимой величиной 
(см. Минковского пространство-время ),можно заключить описание электромагнетизма в компактную форму. Эл—магн. поле в 4-описании может быть задано двумя антисимметричными тензорами
где
— Леви-Чивиты символ ,лат. индексы пробегают значения 1, 2, 3, 4, а греческие — 1, 2, 3. В 4-век-торе тока объединены обычная плотность тока j e и плотность электрич. заряда
аналогично вводят 4-вектор магн. тока.
В этих обозначениях M. у. допускают компактное 4-мерное представление:
Взаимной заменой векторов поля и индукции в ф-лах (13),
(14) вводятся тензоры индукции эл—магн. поля
через к-рые также могут быть записаны M. у.:
Любая пара тензорных ур-ний, содержащая в правых частях оба 4-тока (электрич. и мат.), тождественна системе M. у. Чаще используют пару ур-ний (15 а), (18), при этом материальные ур-ния сводятся к функциональной связи между тензорами 
(последний чаще обозначают через
.
Из антисимметрии тензоров поля, индукции и M. у. в форме (17) — (18) следует равенство нулю 4-дивергенций 4-токов:
к-рое представляет собой 4-мерную запись ур-ний непрерывности для электрич. (магн.) зарядов. T. о., 4-векторы токов являются чисто вихревыми, и соотношения (17), (18) можно рассматривать как их представление в виде 4-роторов соответствующих тензоров. Наряду с представленным здесь вариантом часто используется также 4-мерное описание, в к-ром временная координата (обычно с индексом О) берётся действительной, но 4-мерному пространству приписывается гипербодич. сигнатура 
в таком пространстве приходится различать ко- и контравариантные компоненты векторов и тензоров (см. Ковариантность и контравариантность).
11. Лоренц-инвариантность Максвелла уравнений
Все экспериментально регистрируемые эл—динамич. явления удовлетворяют относительности принципу .Вид M. у. сохраняется при линейных преобразованиях, оставляющих неизменным интервал 
и составляющих 10-мерную Пуанкаре группу: 4 трансляции
, 3 пространственных (орто-) поворота 
и 3 пространственно-временных (орто-хроно-) поворота, иногда называемых ло-ренцевыми вращениями. Последние соответствуют перемещениям системы отсчёта вдоль осей x a с пост, скоростями
В частности, для 
получается простейшая разновидность Лоренца преобразований:
, где 
Соответственно поля преобразуются по правилам:
Релятивистски-ковариантная запись M. у. позволяет легко находить инвариантные комбинации полей, токов и потенциалов (4-скаляров или инвариантов Лоренца группы), сохраняющихся, в частности, при переходе от одной инерциальной системы отсчёта к другой. Во-первых, это чисто полевые инварианты (см. Инварианты электромагнитного поля ).Во-вторых, это токовые (источниковые) инварианты:
В-третьих, это потенциальные инварианты:
где
— магн. потенциалы (получающиеся из А е и 
преобразованием перестановочной двойственности), источниками к-рых являются магн. токи j m и заряды
. И, наконец, многочисл. коыбиниров. инварианты типа
и им подобные. Число таких комбиниров. инвариантов (квадратичных, кубичных и т. д.) по полям н источникам неограниченно.
12. Лагранжиан для электромагнитного поля
M. у. могут быть получены из наименьшего действия принципа, т. е. их можно совместить с Эйлера — Лаг-ранжа уравнениями, обеспечивающими вариационную акстремальность ф-ции действия:
здесь 
— лагранжиан ,являющийся релятивистски-инвариантной величиной; интегрирование ведётся по 4-мерному объёму V, (t 2 — t 1 ) с фиксиров. границами. В качестве обобщённых координат принято обычно использовать потенциалы А a и f. Поскольку лагран-жев формализм должен давать полное (замкнутое) динамич. описание системы, то при его построении нужно принимать во внимание материальные ур-ния. Они фигурируют как зависимости связанных зарядов и токов от полей В и Е·
В результате лагранжиан принимает вид инвариантной комбинации полей, потенциалов и источников:
А ур-ния Эйлера — Лагранжа для нек-рой обобщённой координаты 
получают приравниванием нулю соответствующих вариационных производных:
Для 
приходим к (4), для- 
к ур-нию (1) в соответствующих обозначениях. Вариационный подход позволяет придать теории универсальную форму описания, распространяемую и на описания динамики любых взаимодействий, даёт возможность получать ур-ния для комбиниров. динамич. систем, напр, электромеханических. В частности, для систем с сосредоточенными параметрами, характеризуемых конечным числом степеней свободы, соответствующие ур-ния наз. ур-ниями Лагранжа — Максвелла.
13. Единственность решений Максвелла уравнений
Различают теоремы единственности для стационарных и нестационарных процессов. Условия единственности нестационарных решений извлекаются из Пойн-тинга теоремы, где источники считаются заданными ф-циями координат и времени. Если бы они порождали два разл. поля, то разность этих полей в вакууме (или в любой линейной материальной среде) вследствие принципа суперпозиции была бы решением однородных M. у. Для обращения этой разности в нуль и, следовательно, получения единств, решения достаточно удовлетворить след, трём условиям. 1) На поверхности S, окружающей область V, где ищется поле, должны быть заданы тангенциальные составляющие поля Е тан или поля Н тан либо соотношения между ними импедансного типа: 
(п — нормаль к S) со значениями Z, исключающими приток энергии извне. К таковым относятся, в частности, условия излучения (см. Зоммерфельда условия излучения ),к-рым удовлетворяют волны в однородной среде на больших расстояниях от источников. Во всех случаях поток энергии для разностного поля вообще исчезает или направлен наружу (из объёма). 2) В нач. момент времени должны быть заданы все поля всюду внутри V. 3) Плотность энергии электромагнитного поля 
HB) должна быть положительна (вакуум, среды с 
. Эта частная теорема единственности обобщается на среды с нелокальными связями, а также на нек-рые виды параметрич. сред. Однако в нелинейных средах, где принцип суперпозиции не работает, никаких общих утверждений о единственности не существует.
В стационарных режимах нач. условия выпадают, и теоремы единственности формулируются непосредственно для установившихся решений. Так, в электростатике достаточно задать все источники r e ст , все полные заряды на изолиров. проводниках или их потенциалы, чтобы при соответствующих условиях на бесконечности (нужное спадание поля) решение было бы единственным. Аналогичные теоремы устанавливаются для магнитостатики и электродинамики пост, токов в проводящих средах.
Особо выделяется случай синусоидальных во времени процессов, для к-рых формулируют след, признаки, достаточные для получения единств, решения: 1) задание источников 
задание E тан или Н тан на ограничивающей объём V поверхности S или соответствующих импедансных условий, обеспечивающих отсутствие потока вектора Пойнтинга внутрь V; 3) наличие малого поглощения внутри V или малой утечки энергии через S для исключения существования собств. колебаний на частоте 
14. Классификация приближений Максвелла уравнений
Классификация приближений M. у. обычно основывается на безразмерных параметрах, определяющих и критерии подобия для эл—магн. полей. В вакууме таким параметром является отношение 
, где 
— характерный масштаб изменения полей (либо размер области, в к-рой ищется решение), 
— характерный временной масштаб изменения полей.
а) а = 0 — статич. приближение, статика.
Система M. у. распадается на три.
Материальная связь в простейшем случае имеет вид 
. Это система M. у. для электростатики, в к-рой источниками служат заданные распределения плотности электрич. заряда 
и сторонней поляризации 
. В однородной среде 
эл—статич. потенциал f определяется Пуассона уравнением
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать
Лекция 24
Видео:Уравнение состояния идеального газаСкачать
1.Основные понятия
Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году. По своей значимости они аналогичны законам Ньютона в механике. Современная формулировка дана Герцем и Хевисайдом. Эти уравнения связывают характеристики электромагнитного поля и его источники.
В данные уравнения входят 
— напряженность электрического поля, 
индукция магнитного поля. Эти величины являются основными, т.к. определяют силу, действующую на заряженную частицу (Fл) – силу Лоренца.
Входят две вспомогательные величины 
— индукция электрического поля и 
— напряженность магнитного поля. Также входят 
— плотность тока и ρ — плотность заряда.
Уравнения Максвелла позволяют по известному полю найти токи и заряды (достаточно просто), а также по известным токам и зарядам найти поле (сложно). Уравнения будем писать в СИ в порядке указанном в физической энциклопедии.
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать
2.Интегральная форма
I уравнение представляет собой обобщение закона полного тока.
 | Закон: Циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через произвольную поверхность, охваченную данным контуром. |
II уравнение обобщает закон электромагнитной индукции.
| Закон: Циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения потока магнитной индукции через площадку, охваченную данным контуром, взятой с обратным знаком |
III уравнение: теорема Гаусса для электрической индукции.
| Закон: Поток электрической индукции через произвольную замкнутую поверхность определяется зарядом внутри этой поверхности. |
IV уравнение: закон Гаусса для индукции магнитного поля.
Закон: Поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю.
Видео:идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать
3.Дифференциальная форма
Используя формулы Остроградского-Гаусса и Стокса можно получить
I уравнение Максвелла.
II уравнение Максвелла.
III уравнение Максвелла.
IV уравнение Максвелла
Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать
4.Материальные уравнения
В систему уравнений Максвелла входят 16 скалярных функций координат и времени. Самих уравнений – 8.
Чтобы замкнуть эту систему, используют материальные уравнения.
Величины e, μ, σ получаются из других разделов физики или определяются экспериментально.
🎦 Видео
Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать
Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать
Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать
Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать
Уравнения состояния вещества — Игорь ЛомоносовСкачать
Урок 194. Уравнение Ван-дер-ВаальсаСкачать
Урок 146. Основное уравнение МКТ идеального газа - 2Скачать
Билеты №32, 33 "Уравнения Максвелла"Скачать
Решение биквадратных уравнений. 8 класс.Скачать
1.2 Материальные уравнения, векторы поляризованности и намагниченности средСкачать
Решение задач на основное уравнение МКТ идеального газа | Физика 10 класс #29 | ИнфоурокСкачать
Составление уравнений химических реакций. 1 часть. 8 класс.Скачать
Задачи на уравнение Менделеева-Клапейрона. Ч.1. Краткая теория + решение задачиСкачать
