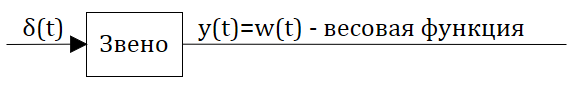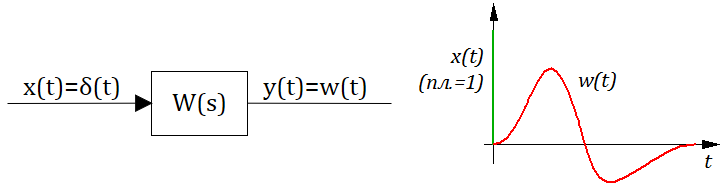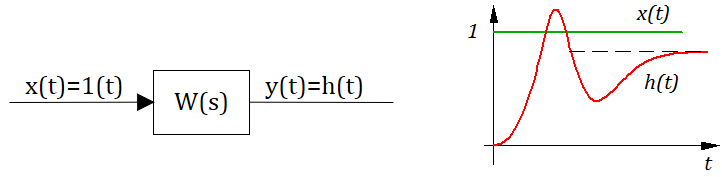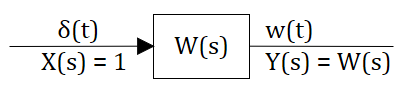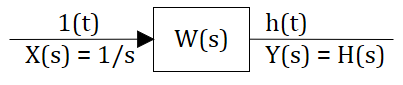Уравнения состояния и передаточная функция

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В предыдущих сериях:

В это части будут рассмотрены:

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.

Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)

Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1

Предположим, что уравнение динамики имеет вид:

где: — постоянные времени;
— коэффициент усиления.

Пусть известны отображения:

Найдем изображения для производных:

Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:

B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.

Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.

После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.

Пример

Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:

входное воздействие: — единичное ступенчатое воздействие.

Выполним преобразование Лапласа:

Подставим в уравнение динамики и получим уравнение динамики в изображениях:

Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:

2.10. Весовая и переходная функции звена (системы).

Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.

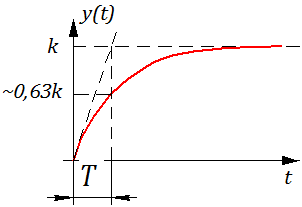
Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.

На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:

Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.

Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):

тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:

Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:

2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона

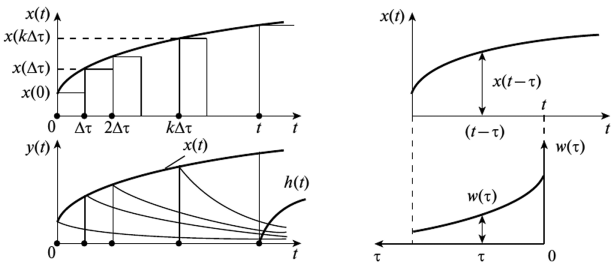
Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).

Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:

где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.

Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:

Переходя к пределам

если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:

где — вспомогательное время

Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:

Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:

2.12. Mетод переменных состояния.

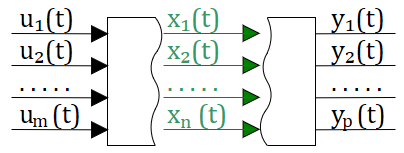
До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)

В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2

В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:

Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:

где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;

Данная система уравнений может быть записана в матричной форме:

где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;

В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.

Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования

Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.

Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики

Пример решения задачи в форме коши.

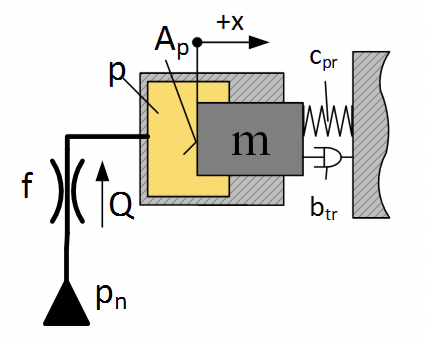
Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:

Дано:
Цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Полость начальным объемом 20 см 3 соединяется с источником давлния дросселем диаметром диаметр которого 0,2 мм. Коэффициент расхода дросселя 0.62. Плотность рабочей жидкости ρ = 850 кг/м 3 .
Определить:
Перемещение дросселя, если в источнике давление происходит скачек 200 бар. см. рис. 2.12.13

Уравенение движение плунжера:

Где: – площадь плунжера, – жесткость пружины, – коэффициент вязкого трения, p – давление в камере.

Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда

Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:

Где: Q – расход в камеру, V — объем камеры.

Расход через дроссель:

Где: f– площадь дросселя, – давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:

Подставляем линеаризованную формул расхода в формулу давления:

Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:

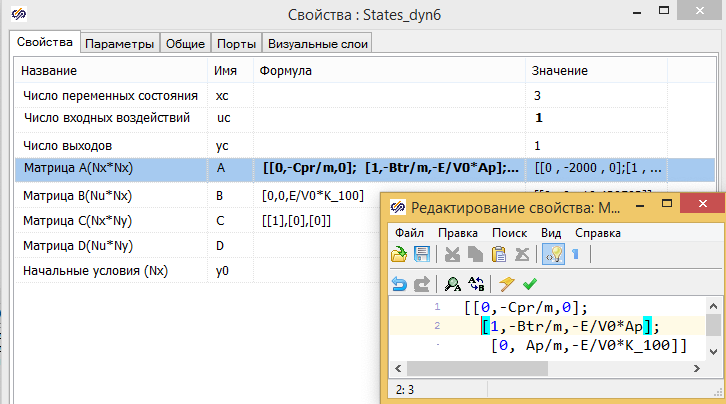
Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:

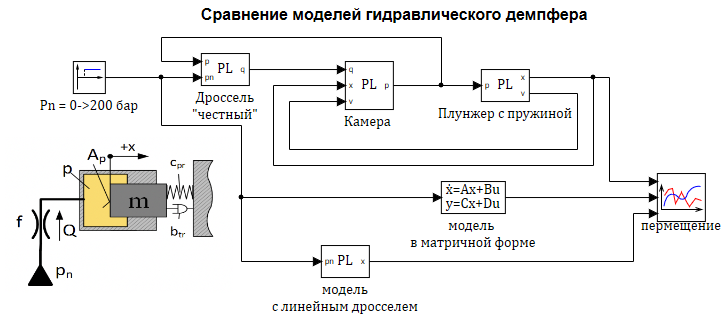
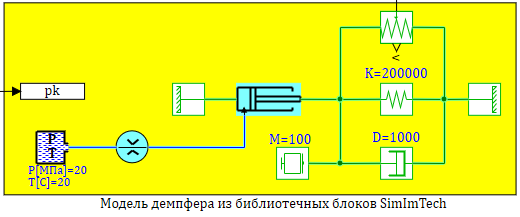
Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.

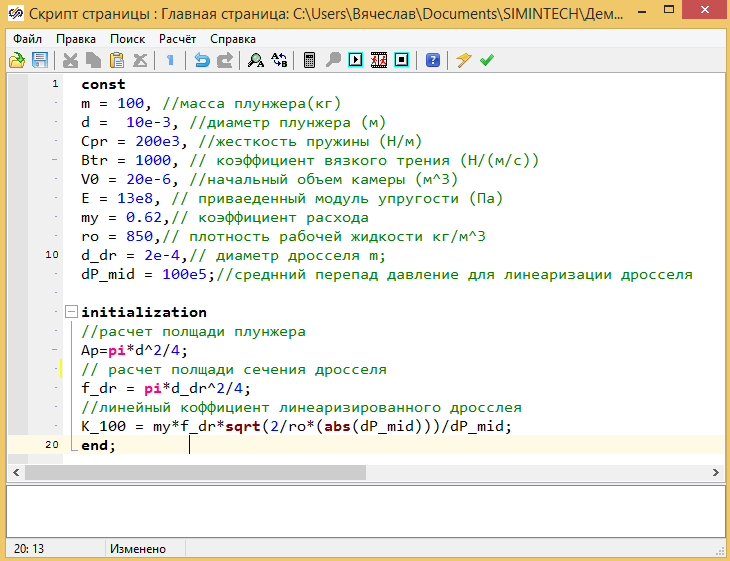
Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:

Рисунок 2.12.5 Глобальный скрипт проекта.

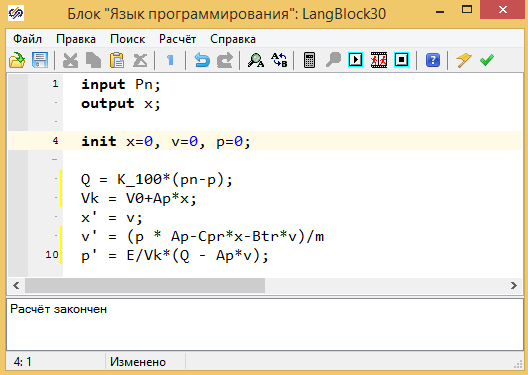
Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)

Рисунок 2.12.6 Скрипт расчета модели в форме Коши.

Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7

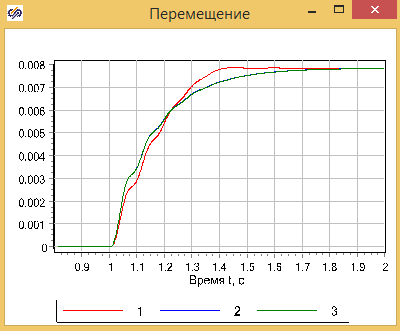
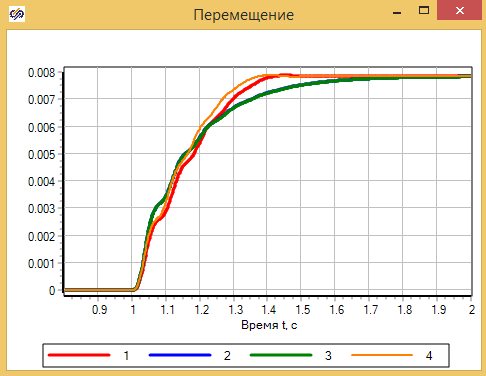
Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)

Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10

На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.

2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно

Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:

Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:

2.13.1. Правая часть содержит только b₀*u(t)

В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.

Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:

Для перехода к форме Коши ведем новые переменные:

И перепишем уравнение относительно y»'(t):

Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:

Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:

2.13.2. Правая часть общего вида

Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:

Сделаем преобразования: перейдем к уравнениям динамики в изображениях:

Тогда можно представить уравнение в изображениях в виде:

Разделим уравнение в изображениях на произведение полиномов , получим:

Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что отображение величины . Тогда входная величина может быть в изображениях представлена как:

Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.

А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:

Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния :

А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:

Перейдем от изображения к оригиналам:

Если обозначить вектор , то мы получим уравнения переменных состояниях в матричной форме, где D = 0:

Пример:

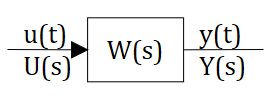
Рисунок 2.13.1 Передаточная функция.

Имеется передаточная функция (рис. 2.13.1) в изображениях :

Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши

В изображения реакция системы связана с входным воздействие соотношением:

Разделим в последнем правую и левую часть на произведения , и введем новую перменную :

Полиномы N(s) и L(s) равны:

Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):

Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:

Или в матричной форме:

Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:

Перейдем от изображений к оригиналу:

Таким образом второе уравнение матричной системы выглядит так:

Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2

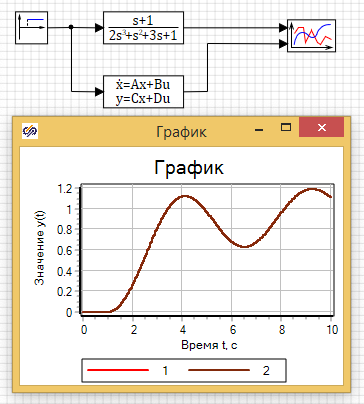
Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.

Видео:8) ТАУ для чайников.Часть 3.6 : Передаточная функция и пространство состояний.Скачать

Связь между передаточной функцией и уравнениями состояния

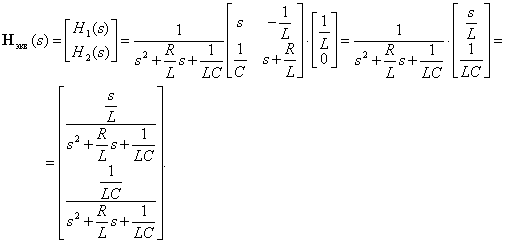
Если задана передаточная функция G(s), то, изобразив модель системы в виде сигнального графа, мы затем можем получить уравнения состояния. Теперь мы решим обратную зада­чу, т. е. покажем, как по уравнениям состояния системы с одним входом и одним выходом определить ее передаточную функцию. Напомним еще раз уравнения (3.16) и (3.17):

Преобразуя эти уравнения по Лапласу, получим:

где В — матрица размерности 77×1, поскольку и есть единственный вход. Заметим, что в преобразовании Лапласа мы не учитывали начальные условия, поскольку определению подлежит передаточная функция. Группируя члены в уравнении (3.68), получим:

Видео:Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Требования к качеству системы в частотной области

Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной …

Измерение частотных характеристик

Синусоидальный сигнал можно использовать для измерения частотных характеристик ра­зомкнутой системы управления. На практике это связано с получением графиков зависи­мости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим …

Пример построения диаграммы Боде

Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отде­льно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем …

Видео:proТАУ: 1. Передаточная функцияСкачать

Продажа шагающий экскаватор 20/90

Цена договорная
Используются в горнодобывающей промышленности при добыче полезных ископаемых (уголь, сланцы, руды черных и
цветных металлов, золото, сырье для химической промышленности, огнеупоров и др.) открытым способом. Их назначение – вскрышные работы с укладкой породы в выработанное пространство или на борт карьера. Экскаваторы способны
перемещать горную массу на большие расстояния. При разработке пород повышенной прочности требуется частичное или
сплошное рыхление взрыванием.
Вместимость ковша, м3 20
Длина стрелы, м 90
Угол наклона стрелы, град 32
Концевая нагрузка (max.) тс 63
Продолжительность рабочего цикла (грунт первой категории), с 60
Высота выгрузки, м 38,5
Глубина копания, м 42,5
Радиус выгрузки, м 83
Просвет под задней частью платформы, м 1,61
Диаметр опорной базы, м 14,5
Удельное давление на грунт при работе и передвижении, МПа 0,105/0,24
Размеры башмака (длина и ширина), м 13 х 2,5
Рабочая масса, т 1690
Мощность механизма подъема, кВт 2х1120
Мощность механизма поворота, кВт 4х250
Мощность механизма тяги, кВт 2х1120
Мощность механизма хода, кВт 2х400
Мощность сетевого двигателя, кВ 2х1600
Напряжение питающей сети, кВ 6
Более детальную информацию можете получить по телефону (063)0416788

Видео:Передаточные функцииСкачать

Уравнения состояния и передаточная функция

Взаимосвязь видов математических моделей многомерных систем

Выше были рассмотрены два вида моделей многомерной системы. Установим связь между этими двумя видами. Так как исходной базой для математических моделей являются дифференциальные уравнения, то логичным будет определить связь уравнений состояния с передаточными матрицами САУ. Для этого применим преобразование Лапласа к уравнениям состояния и выхода

при нулевых начальных условиях, заменим оригиналы переменных изображениями по Лапласу и получим систему векторно-матричных операторных уравнений

Определим связь между вектором входа и векторами состояния и выхода. Из первого уравнения системы (3) имеем –

и если матрица не вырожденная, то есть , получим –

Откуда следует, что

Подставив (4) в (3), получаем –

,

В результате получаем –

Вспомним, что компонентами эквивалентных матриц являются передаточные функции системы. Следовательно, выражения (5) и (6) представляют собой универсальные формулы для вычисления всех необходимых для анализа передаточных функций многомерной системы, по которым могут быть получены структурные схемы и частотные характеристики.

Заметим, что каждый элемент эквивалентных матриц (передаточных функций) имеет, по определению обратной матрицы, сомножитель –

То есть полином является общим знаменателем для всех передаточных функций, а уравнение –

является характеристическим уравнением системы.

Таким образом, мы не только получили связь между математическими моделями во временной и частотной областях, но и универсальные выражения для определения передаточных функций и характеристических уравнений любых линейных объектов или систем управления. Исходными параметрами для выражений (5),(6) и (7) являются матрицы параметров уравнений состояния и выхода. Выполнить преобразования (5),(6) и (7) можно с помощью компьютера, имеющего программы символьной математики, на пример, такие, как Mathematica 3.0 (4.0), разработанные Wolfram Research. в системах второго и третьего порядка эти преобразования можно производить и вручную.

Рассмотрим несколько примеров получения и преобразования моделей.

Рассмотрим объект, принципиальная электрическая схема которого показана на рис. 1.

Выполним для этого объекта следующие задачи:

Получить уравнение состояния.

Определить характеристическое уравнение объекта.

Определить передаточную матрицу объекта.

Получение уравнения состояния

Запишем дифференциальные уравнения, описывающие процессы в схеме

Зададим векторы состояния и входа:

Получаем, что . Запишем уравнение состояния в развернутой форме для нашего случая:

Раскроем в (9) матричные скобки:

Приведем систему уравнений (8) к виду (10), используя при отсутствии переменной в правых частях нулевые коэффициенты:

Теперь известны все компоненты матриц параметров, и можно записать уравнение состояния

.

Следовательно, матрицы параметров имеют следующий вид –

Определение характеристического уравнения объекта

Характеристическое уравнение системы определим по матрицам параметров уравнения состояния (11), используя выражение (7) –

Подставив в (12) выражения для матрицы параметров и единичной матрицы , получим характеристическое уравнение

Определение передаточной матрицы объекта

Определим эквивалентную матрицу передаточных функций, которая связывает векторы состояния и управления по выражению (5), которое для нашего случая имеет вид:

Матрица может быть определена из (13)

.

Определим обратную матрицу, помня о том, – адъюнкт исходной матрицы представляет собой транспонированную матрицу алгебраических дополнений элементов матрицы, а алгебраические дополнения определяются для каждого элемента исходной матрицы по следующему выражению –

,

где – минор исходной матрицы, полученный вычеркиванием — ой строки и -го столбца.

.

Следовательно, получаем передаточные функции объекта

.

Электродвигатель постоянного тока независимого возбуждения (с постоянными магнитами) как объект управления описывается следующей системой дифференциальных уравнений –

где – напряжение, подаваемое на двигатель, – скорость и ток двигателя, – параметры двигателя, соответственно момент инерции, сопротивление и индуктивность обмотки якоря, конструктивный коэффициент.

Получение уравнения состояния

Зададим векторы состояния и входа:

Получаем, что . Запишем уравнение состояния в развернутой форме для нашего случая:

Раскроем в (16) матричные скобки:

Приведем систему уравнений (15) к виду (17), используя при отсутствии переменной в правых частях нулевые коэффициенты:

Теперь известны все компоненты матриц параметров, и можно записать уравнение состояния в развернутой форме

.

Следовательно, матрицы параметров имеют следующий вид –

Определение характеристического уравнения объекта

Характеристическое уравнение системы определим по матрицам параметров уравнения состояния (18), используя выражение (7) –

Подставив в (19) выражения для матрицы параметров и единичной матрицы , получим характеристическое уравнение

Определение передаточной матрицы объекта

Определим эквивалентную матрицу передаточных функций, которая связывает векторы состояния и управления по выражению (5), которое для нашего случая имеет вид:

Матрица может быть определена из (20)

.

Определим обратную матрицу –

.

Следовательно, получаем передаточные функции объекта

Контрольные вопросы и задачи

Поясните, как связаны между собой модели во временной и частотной области?

Как определить по уравнению состояния характеристическое уравнение?

Как определить по уравнению состояния матрицу передааточных функций системы?

По уравнению состояния

,

описывающему многомерную систему, определить характеристическое уравнение системы.

.

По уравнению состояния

,

описывающему многомерную систему, определить характеристическое уравнение системы.

.

По уравнению состояния

,

описывающему многомерную систему, определить матрицу передаточных функций системы.

.

🔥 Видео

[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать

Уравнение состояния идеального газа. 10 класс.Скачать

7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

Метод пространства состояний САУ: описание конкретной системыСкачать

Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

ТАУ│Передаточная функция устройстваСкачать

Теория автоматического регулирования. Лекция 5. Модели параметров состоянийСкачать

Построить структурную схему САР (САУ) по передаточной функцииСкачать

2) ТАУ для чайников. Часть 2.1: Математические модели...Скачать

23) Построение Л.А.Ч.Х. и Л.Ф.Ч.Х. системы по её передаточной функцииСкачать

3,9 Уравнения состояния АДСкачать

c15 2, Пространство состояний: пространство состояний передаточная функцияСкачать

Логарифмическая амплитудная характеристика САУ: построение ЛАХ для конкретной системыСкачать

Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Математика это не ИсламСкачать