И пористой среды
Дифференциальные уравнения движения (2.4) и уравнения неразрывности (2.11) содержат в себе параметры r,k,m, и m, представляющие собой характеристики состояния флюида и пористой среды. Для дальнейших расчетов необходимо знать зависимости этих параметров от давления — r(Р), m(Р), k(Р), m(Р).
1. При установившейся фильтрации капельной жидкости можно считать ее плотность не зависящей от давления, т.е. рассматривать жидкость как несжимаемую, тогда r=const.
При неустановившихся процессах фильтрации, когда значительный объем пластовой жидкости (нефти) отбирается за счет расширения ее объема при снижении ее пластового давления, капельную жидкость следует считать упругой. Закон сжимаемости упругой жидкости имеет вид
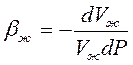
где Vж — начальный объем жидкости; dVж — изменение начального объема жидкости при изменении давления на величину dP; bж — коэффициент объемного сжатия жидкости, который считается постоянным и не зависит от давления и температуры;
для нефтей bн = (7¸30)*10 -10 Па -1 ;
для пластовых вод bВ = (2,5¸5)*10 -10 Па -1 .
Преобразуем (2.13), учитывая что
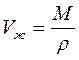
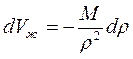
Получаем 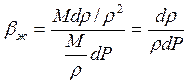
откуда 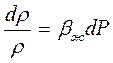
Интегрируем последнее равенство от фиксированных значений Р0 и r0 до текучих Р и r соответственно
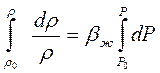
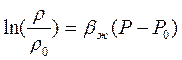
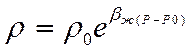
Обычно показатель степени bж(Р-Р0) значительно меньше единицы. Поэтому разложим функцию 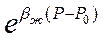
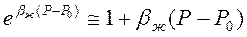
Получаем линейную зависимость плотности от давления
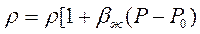
2. Природные газы можно считать идеальными (совершенными), если пластовые давления газовых месторождений невелики (до 6-9 МПа) и газ отбирается при депрессии до 1 МПа. Уравнением состояния идеального газа является уравнение Меделеева-Клапейрона
PV = MRT или 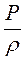
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Уравнение состояния вещества
Параметры состояния связаны друг с другом. Соотношение, при котором определяется данная связь, называют уравнением состояния данного тела. В самом простом случае равновесное состояние тела определяется значением следующих параметров: давления p , объема V и температуры (масса тела или системы, как правило, известна).
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Что такое идеальный газ
Уравнение состояния так называемого идеального газа является простым, но достаточно информативным.
Идеальный газ – это газ, в котором пренебрегают взаимодействием молекул между собой.
Идеальными считают разреженные газы. Особенно близки к идеальным газы гелий и водород. Идеальный газ – это упрощенная математическая модель реального газа: молекулы движутся хаотически, а соударения между молекулами и удары молекул о стенки сосуда упругие, не приводящие к потерям энергии в системе. Подобная упрощенная модель весьма удобна, поскольку не требует учета силы взаимодействия между молекулами газа. Множество реальных газов не отличаются в своем поведении от идеального газа в условиях, когда суммарный объем молекул пренебрежимо мал в сравнении с объемом сосуда (то есть при атмосферном давлении и комнатной температуре). Это дает возможность применять уравнение состояния идеального газа для сложных расчетов.
Уравнение состояния идеального газа запишем несколько раз ( 2 ) , ( 3 ) , ( 5 ) :
p V = m μ R T = ν R T ( 2 ) .
Уравнение ( 2 ) – уравнение Менделеева-Клапейрона, где m – это масса газа, μ – это молярная масса газа, R = 8 , 31 Д ж м о л ь · К – это универсальная газовая постоянная, ν – это число молей вещества.
где N – это количество молекул газа в массе m , k = 1 , 38 · 10 — 23 Д ж К , постоянная Больцмана, определяющая «долю» газовой постоянной, которая приходится на 1 молекулу и
N A = 6 , 02 · 10 23 м о л ь — 1 – это постоянная Авогадро.
Если поделить в ( 4 ) обе части на V , то получаем следующий вид записи уравнения состояния идеального газа:
где n = N V – это количество частиц в единице объема или же концентрация частиц.
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Что такое реальный газ
Рассмотрим теперь более сложные системы: неидеальные газы и жидкости.
Реальный газ – это газ, между молекулами которого наблюдаются заметные силы взаимодействия.
Необходимо учитывать, что в неидеальных, плотных газах взаимодействие молекул высоко. Известно, что взаимодействие молекул очень сильно усложняет физическую картину, потому точную формулу уравнения состояния неидеального газа не получается записать в простом виде. В данном случае прибегают к приближенным формулам, найденным полу-эмпирическим путем. Самая удачная формула – это уравнение Ван-деp-Ваальса.
Взаимодействие молекул обладает сложным характером. На достаточно больших расстояниях между молекулами действуют силы притяжения. С уменьшением расстояния силы притяжения вначале растут, однако потом уменьшаются и преобразуются в силы отталкивания. Притяжение и отталкивание молекул будем рассматривать и учитывать отдельно. Уравнение Ван-дер-Ваальса, которое описывает состояние одного моля реального газа, имеет вид:
p + a V μ 2 V μ — b = R T ( 6 ) ,
где a V μ 2 – это внутреннее давление, обусловленное силами притяжения между молекулами, b – это поправка на собственный объем молекул, учитывающая действие сил отталкивания между молекулами, при этом:
b = N A 2 3 πd 3 ( 7 ) ,
где d – это диаметр молекулы. Значение a рассчитывается по формуле:
a = — 2 πN A 2 ∫ d ∞ W p ( r ) r 2 dr ( 8 ) ,
где W p ( r ) – это потенциальная энергия притяжения 2 -х молекул.
При увеличении объема значение поправок в уравнении ( 6 ) становится менее существенным. И в пределе уравнение ( 6 ) превращается в уравнение ( 2 ) . Это согласовано с тем фактом, что с уменьшением плотности реальные газы по своим характеристикам приближаются к идеальным.
Положительным в уравнении Ван-деp-Ваальса является тот факт, что данное равенство при очень больших плотностях приблизительно описывает также и свойства жидкости, в частности, плохую ее сжимаемость. Потому существует основание предполагать, что уравнение Ван-деp-Ваальса позволяет отразить и переход от жидкости к газу (либо от газа к жидкости).
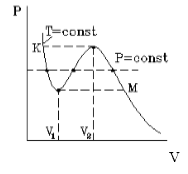
На рисунке 1 представлена изотерма Ван-дер-Ваальса для некоторого постоянного значения температуры T , которая построена из соответствующего уравнения.
В месте “извилины” (участок КМ) изотерма 3 раза пересекает изобару. На участке
V 1 , V 2 давление увеличивается с ростом объема.
Подобная зависимость невозможна. Это означает, что в этой области с веществом происходит что-то необыкновенное. Что именно, не видно в уравнении Ван-деp-Ваальса. Обратимся к опыту. В месте “извилины” на изотерме в состоянии равновесия вещество расслаивается на 2 фазы: жидкую и газообразную. Обе фазы существуют одновременно и находятся в фазовом равновесии. В таком состоянии происходит испарение жидкости и конденсация газа. Процессы протекают с такой интенсивностью, что полностью компенсируют друг друга: объем жидкости и газа со временем не изменяется.
Газ, который находится в фазовом равновесии со своей жидкостью, называется насыщенным паром. Если фазовое равновесие отсутствует, отсутствует также компенсация испарения и конденсации, тогда газ называется ненасыщенным паром.
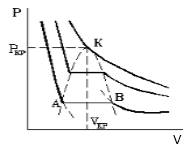
Что происходит с изотермой в области двухфазного состояния вещества (то есть в месте «извилины» изотермы Ван-деp-Ваальса)? Эксперимент показывает, что в этом месте при изменении объема давление остается неизменным. График изотермы идет параллельно оси V (рисунок 2 ).
С увеличением температуры участок двухфазных состояний на изотермах уменьшается до тех пор, пока не превращается в точку (рисунок 2 ). Это особая точка К , в которой исчезает разница между жидкостью и паром. Ее называют критической точкой.
Параметры, которые соответствуют критическому состоянию, являются критическими (критическая температура, критическое давление, критическая плотность вещества).
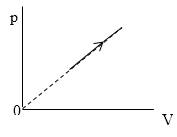
Необходимо найти величину n . В процессе, представленном на рисунке 3 , давление p
Из графика, приведенного на рисунке 3 , запишем уравнение процесса в параметрах p ( V ) :
С учетом уравнения Менделеева-Клайперона:
V вместо объема, получаем:
Моль кислорода охлаждают до — 100 ° C . Необходимо определить давление, которое оказывает газ на стенки сосуда, если занимаемый газом объем V = 0 , 1 л . Необходимо также сравнить p с давлением идеального газа p i d , если бы кислород вел себя как идеальный газ. Величина постоянных Ван-дер-Ваальса a и b , для кислорода a = 0 , 1358 П а · м 6 / м о л ь 2 , b = 3 , 167 · 10 — 5 м 3 / м о л ь .
Из уравнения Ван-Дер-Ваальса имеем:
p = R T V μ — b — a V μ 2
Переведем температуру в систему измерения: T = t + 273 , По условию T = 173 K , V = 0 , 1 л = 10 — 4 м 3 .
Произведем расчет: p = 8 , 31 · 173 ( 10 — 3 , 2 ) · 10 — 5 — 0 , 1358 ( 10 — 4 ) 2 = 75 , 61 · 10 5 ( П а ) .
Для идеального газа:
Рассчитаем: p i d = 1 · 8 , 31 · 173 10 — 4 = 143 · 10 5 ( П а ) .
Видео:Уравнение состояния идеального газаСкачать

Конспект лекций
по общей химии
Продолжение.
Начало см. в № 8, 12, 13, 20, 23, 25-26, 40/2004;
1, 11, 15/2005;
7/2006
Видео:Уравнение состояния идеального газаСкачать

Глава 8. Строение вещества
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

8.1. Агрегатные состояния вещества
Химики изучают превращения веществ, находящихся в трех агрегатных состояниях – газообразном (газы), жидком (жидкости) и твердом (твердые аморфные тела либо кристаллы) (табл. 8.1).
Свойства газов, жидкостей, твердых веществ
Плотность
Совпадает с объемом сосуда, сильно зависит от температуры и давления
Заполняет сосуд, принимая его форму
Высокая
Низкая
Жидкость
Фиксированный
Нефиксированная, полностью или частично заполняет сосуд
Малая
От умеренной до большой
Твердое вещество
Фиксированный
Собственная
Практически отсутствует
Большая
Газы. Наиболее характерным свойством является сжимаемость и способность расширяться. Газы не имеют собственной формы, они расширяются до тех пор, пока равномерно не заполнят весь сосуд, куда их поместили. Это означает, что газы не имеют собственного объема, т.е. объем газа определяется объемом сосуда, в котором он находится. Газ оказывает на стенки сосуда давление, одинаковое во всех направлениях. Еще одним свойством газов является их способность смешиваться друг с другом в любых соотношениях.
Жидкости. Подобно газам, жидкости не имеют определенной формы. Жидкость принимает форму того сосуда, в котором она находится, при установившемся под влиянием силы тяжести некотором ее уровне. Однако в отличие от газа жидкость имеет собственный объем. Сжимаемость жидкостей очень мала. Для того чтобы заметно сжать жидкость, требуется очень высокое давление.
Твердые вещества. Твердые тела отличаются от жидкостей и газов наличием собственной формы и определенного объема. Сжимаемость твердых тел чрезвычайно мала даже при очень высоких давлениях.
Газообразному состоянию присущи две особенности:
1) расстояние между молекулами обычно в несколько раз превышает их размеры;
2) газы способны занимать весь объем предоставленного им пространства.
Газы в отличие от жидкостей и твердых тел могут сравнительно легко сжиматься. Для того чтобы хорошо понимать особенности строения газообразного вещества, нужно знать, чему равен молярный объем газа, какова взаимосвязь между занимаемым газом объемом и количеством вещества, температурой и давлением, как определить среднее расстояние между молекулами газа и как оно зависит от его давления, с какой скоростью двигаются молекулы газообразного вещества и от чего эта скорость зависит.
Молярный объем газа – постоянная величина, поскольку она мало зависит от природы вещества. Молярный объем при давлении 1 атм (101,3 кПа) и температуре 0 °С (273 K) по закону Авогадро равен 22,4 л. Газ, строго подчиняющийся закону Авогадро, принято называть идеальным.
Выбранные условия (1 атм, 0 °С) названы нормальными (н.у.). В школьных курсах химии и физики незначительными отклонениями свойств реальных газов от вытекающих из закона Авогадро для идеального газа пренебрегают. Естественно, что молярный объем газа зависит от температуры и давления. При 25 °С и давлении 1 атм (эти условия названы стандартными) молярный объем идеального газа равен уже 24,4 л.
Молярные объемы реальных газов при одних и тех же условиях несколько отличаются от молярного объема идеального газа (табл. 8.2).
🔍 Видео
Урок 25 (осн). Задачи на взаимодействие телСкачать

Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Парадокс сужающейся трубыСкачать

Различия в молекулярном строении газов, жидкостей и твердых тел | Физика 7 класс #8 | ИнфоурокСкачать

Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Урок 146. Основное уравнение МКТ идеального газа - 2Скачать

Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

ЕГЭ по физике. Теория #25. Идеальный газ. Уравнение состояния идеального газаСкачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Сжимаемость газов и жидкостей. ФизикаСкачать