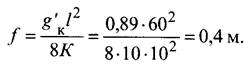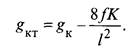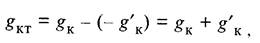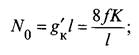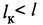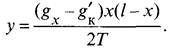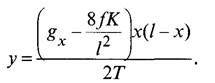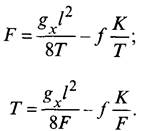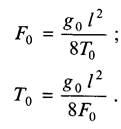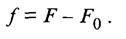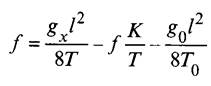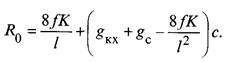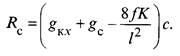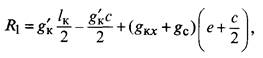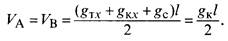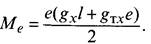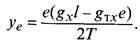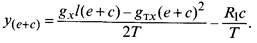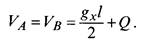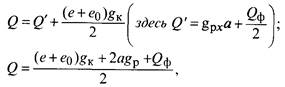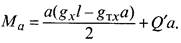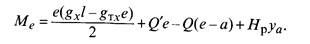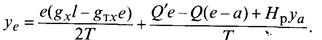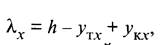Уравнения состояния для простой подвески (4 видео)

Уравнение провисания несущего троса цепных подвесок

Общие понятия. Основной частью расчета цепной подвески является расчет натяжений и стрел провеса несущего троса. Особенность этого расчета заключается в том, что несущий трос цепной подвески, кроме нагрузки от собственного веса и дополнительных нагрузок от гололеда и ветра, воспринимает также нагрузки от подвешенных к нему контактных и вспомогательных проводов, включая и дополнительные нагрузки от гололеда, а в некоторых случаях и ветра на эти провода. Значение нагрузки, передающейся с контактного провода на несущий трос, зависит от стрел провеса и натяжений вспомогательного и контактного проводов.

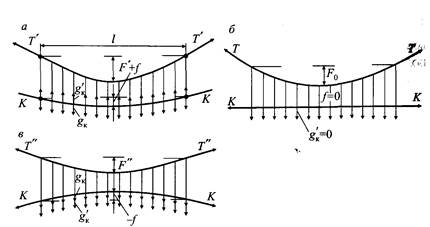
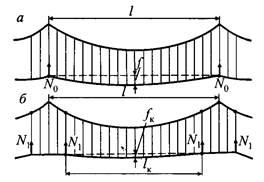
Рассмотрим схемы нагрузок, действующих на контактный провод при различном его расположении в вертикальной плоскости (рис. 14.6). Как видно на рис. 14.6, а, на контактный провод действуют равномерно распределенная нагрузка g_K от веса провода и равномерно распределенная нагрузка g’_K, обусловленная натяжением контактного провода.

Нагрузку g_K в пролете l при натяжении контактного провода К и его провеса находят из соотношения , откуда имеем^

Рис. 14.6. Схемы нагрузок, действующих на контактный провод при различном его расположении в вертикальный плоскости: а, в — при положительной и отрицательной стрелах провеса; б — при беспровесном положении

В случае положительной стрелы провеса контактного провода (+f) нагрузка g’_K будет положительной и направленной вверх. На несущий трос с контактного провода в этом случае будет передаваться равномерно распределенная нагрузка

При определенной положительной стреле провеса контактного провода нагрузка g’_K может оказаться равной g_K. В этом случае g_KT = О, так как контактный провод под действием его натяжения К оказался полностью самонесущим: на несущий трос через струны не передается никакая нагрузка от веса контактного провода.

Например, контактный провод МФ-100, имеющий натяжение К = 10 кН, будет полностью самонесущим (g’_K = g_K = 0,89 даН/м) в пролете 60 м, когда его стрела провеса

В случае такой стрелы провеса контактного провода вес его будет восприниматься вертикальными струнами и передаваться через них на поддерживающие устройства: все другие струны в пролете разгружены.

В компенсированных цепных подвесках контактный провод монтируют со стрелой провеса, равной примерно 0,001 l, т.е. при l_к= 60 м стрела провеса контактного провода даже при наивысшей температуре окружающего воздуха меньше, чем у свободно подвешенного контактного провода в пролете l. Поэтому в цепных подвесках контактный провод несет сам только часть нагрузки от собственного веса, действующего на него, другая часть g_KT через струны передается на несущий трос.

Подставляя значения g’_K, получим

При беспровесном положении контактного провода (рис. 14.6, б) f = 0, следовательно, g’_K = 0. Контактный провод в этом случае сам не несет никакой нагрузки, последняя полностью передается на несущий трос: g_KJ = g_K.

При отрицательных стрелах провеса контактного провода (рис. 14.6, в), которые могут быть в полукомпенсированных подвесках, g’_K будет отрицательной (направленной вниз). В этом случае

т.е. несущий трос будет нести не только нагрузку g_K от веса контактного провода и действующих на него дополнительных нагрузок, но также и нагрузку g’_K, обусловленную натяжением контактного провода.

Нагрузку g’_K контактный провод в виде сосредоточенных сил передает через крайние струны его пролета на поддерживающие устройства (консоли) при l_к = l (рис. 14.7, а) или непосредственно на несущий трос, когда длина части пролета /_к, в которой контактный провод имеет провес, меньше длины пролета несущего троса (рис. 14.7, б).

Сосредоточенная сила при l_к = l

сосредоточенная сила при

Рис. 14.7. Схемы передачи сосредоточенных сил на несущий трос от нагрузки, обусловленной вертикальной составляющей натяжения контактного провода: а — при l = l_к; б — при l > l_к

Выведем уравнения провисания несущего троса цепной подвески для некоторых схем нагрузок, передающихся на несущий трос с контактного провода. Состояние равновесия цепной подвески будем рассматривать в вертикальной плоскости.

Для вывода уравнений провисания несущего троса цепных подвесок различных конструкций примем следующие обозначения:

l — длина пролета несущего троса, м;

l_к — длина части пролета, в которой контактный провод имеет провес, м;

а — расстояние от опоры до точки закрепления троса рессорных струн на несущем тросе, м;

у — провес несущего троса на расстоянии х от опоры, м;

у_а — провес несущего троса на расстоянии а от опоры, м;

е — расстояние от опоры до первой простой (нерессорной) струны, м;

е₀ — расстояние от опоры до первой струны на проводе рессорных струн, м;

у_е — провес несущего троса на расстояние е от опоры, м;

с — длина струнового пролета контактного провода, м;

q — результирующая нагрузка на несущий трос при соответствующем расчетном режиме, даН/м;

g’_x — вертикальная составляющая этой нагрузки, даН/м;

g_x — вертикальная нагрузка на несущий трос от веса всех проводов цепной подвески и гололеда на них (при его наличии), даН/м;

g₀ — вертикальная нагрузка на несущий трос от веса проводов цепной подвески при беспровесном положении контактного провода, даН/м;

g_T — нагрузка от веса несущего троса, даН/м;

Т— горизонтальная составляющая натяжения несущего троса, кН;

T₀ — горизонтальная составляющая натяжения несущего троса полукомпенсированной подвески при беспровесном положении контактных проводов, или номинальное (начальное) натяжение несущего троса компенсированной подвески, кН;

Н_х — горизонтальная составляющая натяжения ненагруженно-го несущего троса при температуре t_x, кН;

К — сумма натяжений контактных проводов (в двойной цепной подвеске также и вспомогательного провода), кН;

Н — горизонтальная составляющая натяжения провода рессорных струн, кН;

Fq — стрела провеса несущего троса в плоскости действия результирующей нагрузки в пролете l, м;

F₀ — вертикальная стрела провеса несущего троса при беспровесном положении контактных проводов, м;

F — вертикальная стрела провеса несущего троса, м:

F_qk — стрела провеса несущего троса в пролете f_к в плоскости действия результирующей нагрузки, м;

F_K — вертикальная стрела провеса несущего троса в пролете f_к, м;

f_к0 — вертикальная стрела провеса несущего троса в пролете /_к при беспровесном положении контактных проводов, м;

f— стрела провеса контактного провода в пролете l, м;

f_к — стрела провеса контактного провода в пролете l_к, м.

Наиболее простой расчетной схемой является схема, при которой с контактного провода на несущий трос (через большое количество струн) передается равномерно распределенная по всему пролету вертикальная нагрузка. В действительности же с контактного провода на несущий трос передаются через несколько струн вертикальные сосредоточенные нагрузки, а в рессорных подвесках — еще и горизонтальные от натяжения проводов рессорных струн (тросов). Расчетную схему выбирают в зависимости от конструкции и параметров цепной подвески, а также от точности, с которой должны быть рассчитаны провесы несущего троса подвески в различных точках пролета.

Уравнение провисания несущего троса цепной подвески при равномерно распределенной нагрузке. Для вывода уравнения провисания несущего троса цепной подвески при передающейся с контактного провода на несущий трос (большим количеством струн) равномерно распределенной по всему пролету вертикальной нагрузки воспользуемся схемами, показанными на рис. 14.8. Опорные реакции в точках А

Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Рис. 14.8. Схема к выводу уравнения провисания несущего троса цепной подвески с большим количеством струн в пролете

и В в этом случае:

Изгибающий момент в сечении троса на расстоянии х от опоры А:

Для несущего троса цепной подвески, так же как и для свободно подвешенного провода, у = M_x JT. Подставив в него значение М_х, найдем у =’g> (/ —х)/(2Т). Поскольку g’_x = g_x — g’_K, то

Подставив в это уравнение значение g’_K, получим

Для х = I /2 величина у = F и формула примет вид:

Подставив последнее значение Т, получим

Выражения могут быть записаны в следующем виде:

В таком виде они показывают влияние натяжения контактного провода при различных стрелах его провеса на стрелу провеса и натяжение некомпенсированного несущего троса. При положительных значениях f натяжение некомпенсированного несущего троса меньше, а при отрицательных — больше его натяжения T_о при беспровесном положении контактного провода.

Приняв в выражениях (14.2) и (14.3) f = 0, получим

Стрела провеса контактного провода f может быть представлена как разность стрел провеса несущего троса F и F₀, т.е.

Тогда можно записать так:

Величина, стоящая в скобках, играет роль эквивалентной переменной (зависящей от F – F₀) нагрузки. Следовательно, расчет

несущего троса цепной подвески — тот же расчет свободно подвешенного провода (гибкой нити), но с переменной нагрузкой:

Подставив значения F и F₀ получим

и после соответствующих преобразований

Если в уравнения 14.2 и 14.3 вместо f подставить его значение, то после соответствующих преобразований имеем:

Рассматривая эти выражения, видим, что для определения F (компенсированной и полукомпенсированной подвесок) и T (полукомпенсированной подвески) необходимо знать T₀, т.е. номинальное (начальное) натяжение несущего троса компенсированной подвески или соответственно натяжение несущего троса полукомпенсированной подвески при беспровесном положении контактных проводов.

Приведенные формулы даны для расчета провисания несущего троса цепной подвески при передающейся с контактного провода на несущий трос равномерно распределенной вертикальной нагрузки через большое количество струн в пролете. Обычно же в цепных подвесках, особенно с одним контактным проводом, устанавливают всего лишь несколько струн. Поэтому с целью повышения точности расчетов нагрузки, передающиеся с контактного провода на несущий трос, целесообразно рассматривать не как равномерно распределенные по всему пролету, а как сосредоточенные в местах установки струн цепной подвески. Найдем эти нагрузки по схемам расположения струн в пролете, показанным на рис. 14.9.

Рис. 14.9. Схемы сосредоточенных сил, передающихся с контактного провода на несущий трос через простые струны, установленные у опор (а) и смещенные от опор (б)

Для схемы рис. 14.9, а имеем:

где R₀ — сосредоточенная вертикальная нагрузка в местах установки струн под опорами;

g_KX — нагрузка от веса контактного провода и гололеда на нем (при его наличии), даН/м;

g_c — нагрузка от веса струн и зажимов, даН/м.

Подставляя в это выражение значение g’_K, найдем:

Для схемы рис. 14.9, б имеем:

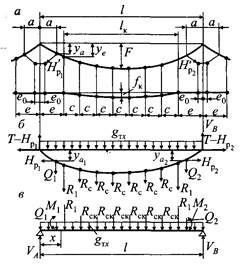
Уравнение провисания несущего троса цепной подвески при сосредоточенных вертикальных нагрузках. Для вывода уравнения провисания несущего троса цепной подвески при передающихся с контактного провода в местах установки струн сосредоточенных вертикальных нагрузках R воспользуемся схемами, приведенными на рис. 14.10. Несущий трос будем рассматривать как сво-

Рис. 14.10. Схемы к выводу уравнения провисания несущего троса цепной подвески: а — со смещенными от опор простыми струнами при небольшом количестве струн в пролете; б — опорные реакции

бодно подвешенный провод, нагруженный равномерно распределенной нагрузкой от собственного веса g_TX и сосредоточенными силами R^ и R_CK.

Поскольку для схемы рис. 14.10, а нагрузка от веса контактного провода и гололеда на нем в пролете / полностью передается на несущий трос, то опорные реакции для схемы рис. 14.10, б будут:

Изгибающий момент на участке отх = 0до.х = ев соответствии со схемой рис. 14.10, б:

При х = е получим

Тогда провес несущего троса на расстоянии е от опоры

Изгибающий моментна участке от х = 0 до л: = (е + с)

При х = е + с получим

Провес несущего троса на расстоянии е + с от опоры (в точке крепления к тросу второй от опоры струны)

Составив аналогичные уравнения изгибающих моментов для других точек несущего троса, в которых установлены струны (например, х = е + 2с и т.д.), можно найти его провесы в этих точках.

Уравнение провисания несущего троса цепной подвески при сосредоточенных вертикальных и горизонтальных нагрузках. На несущий трос рессорных цепных подвесок, кроме нагрузки от собственного веса и нагрузок, передающихся с контактного провода через струны, действуют сосредоточенные нагрузки Н’_р, обусловленные

Рис. 14.11. Схема к выводу уравнения провисания несущего троса рессорной цепной подвески: а — действующие вертикальные нагрузки; б — вертикальные и горизонтальные нагрузки; в — опорные реакции

натяжением рессорных струн. Эти нагрузки приложены к несущему тросу на расстоянии а от опор и направлены вниз под небольшим углом к горизонтали (рис. 14.11, а). Нагрузки от натяжения рессорных струн можно заменить горизонтальными нагрузками Н и вертикальными Q, действующими в плоскости цепной подвески (рис. 14.11, б). Таким образом, в рессорных цепных подвесках несущий трос, кроме вертикальных, воспринимает также горизонтальные нагрузки, направленные вдоль несущего троса. В результате этого он имеет неодинаковое натяжение по длине пролета: в средней части (на длине l — 1а) — натяжение Т, у опор (на длине а с каждой стороны от опоры) — натяжение Т- Н .

Натяжение рессорных струн (тросов) Н’ , которое ввиду малости углов их наклона к горизонтали можно считать равным Н , достигает 1,5—4,0 кН, что составляет от 10 до 30 % натяжения несущего троса Т. Натяжения рессорных струн (тросов), составляющие большую долю натяжения несущего троса, оказывают существенное влияние на форму кривой его провисания в пролете.

Натяжение для несущего троса рессорной цепной подвески, когда на него, кроме вертикальных, действуют также горизонтальные нагрузки, рассчитывается выражением у_х = M_x/T_X.

Схема загружения простой балки для этого случая показана на рис. 14.11, в. Изгибающие моменты от горизонтальных сил Н ^ и Я_р2 соответственно: М_у = Н_р1у_а1; М₂ = Н_py_а1.

Опорные реакции складываются из реакций от вертикальных сил V и реакции от горизонтальных сил V», т.е.

Реакция от горизонтальных сил Н₁ и Н₂

Из этого видно, что при одинаковых параметрах (Я_р и а) проводов рессорных струн (тросов), как это обычно имеет место в рессорных подвесках, реакции V»_A — V»_B — 0. Реакции V_a и V_bub этом случае для схемы рис. 14.11, в определяются:

Вертикальная нагрузка, действующая на несущий трос на расстоянии а от опоры:

где g_p — нагрузка от веса тросов рессорных струн (с учетом зажимов), даН/м;

Q_ф — вертикальная нагрузка от фиксатора, передающаяся тросом рессорных струн на несущий трос, даН/м.

Изгибающий момент на участке х = 0 до х = асоответствии со схемой рис. 14.11, в

При х = а получим

На рассматриваемом участке несущий трос имеет натяжение Т — Т — Н . Провес его на расстоянии а от опоры

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Изгибающий момент на расстоянии е от опоры

Подставляя соответствующие значения входящих в это выражение величин, получим

Провес несущего троса на расстоянии е от опоры (в точке крепления к тросу первой простой струны)

Провес несущего троса на расстоянии е + с от опоры (в точке крепления к тросу второй простой струны) можно определить из выражения

Аналогично можно составить уравнения балочных изгибающих моментов и для других точек (например, х = е + 2с и т. д.) несущего троса, в которых установлены струны, а затем найти провесы троса в этих точках.

Значения величин Q и Q’ в большей степени зависят от того, подвешен ли основной стержень сочлененного фиксатора к несущему тросу или к рессорной струне. В последнем случае нагрузки Q и Q оказывают большое влияние на форму кривой провисания несущего троса, и поэтому их необходимо учитывать в расчетах.

С помощью приведенных формул можно определить провесы несущего троса цепной подвески в любой точке пролета и подсчитать длины струн. Это особенно важно для компенсированных подвесок, эксплуатирующихся при скоростях движения более 160 км/ч, поскольку правильная регулировка контактного провода по высоте при монтаже зависит от принятых в ре-

Рис. 14.12. Схема для определения длины струн цепных подвесок

зультате расчетов длин струн.

При определении длины струн полукомпенсированных цепных подвесок рассматривают подвеску в режиме беспровесного положения контактных проводов. В компенсированных подвесках учитывают провес контактного провода (рис. 14.12) по формуле

где Х_х — длина струны, смонтированной на расстоянии х от опоры, м;

h — конструктивная высота цепной подвески, м;

у_тх — провес несущего троса на расстоянии х от опоры, м;

у_кх — провес контактного провода (в компенсированных подвесках) на расстоянии х от опоры, м.

Провес несущего троса у_тх можно определить по полученным формулам в зависимости от конструкции контактной подвески. Для определения провеса контактного провода у_кх можно воспользоваться формулой

Уравнения состояния для простой подвески

3.5. Расчет цепных контактных подвесок

Расчет натяжений и стрел провеса несущего троса. Особенностью механического расчета несущего троса цепной подвески является то, что кроме нагрузок от собственного веса и временных на грузок на него от гололеда и ветра он воспринимает также дополнительные нагрузки от веса контактных и вспомогательных проводов, а также от действия гололеда и ветра на эти провода. Величина этих дополнительных нагрузок колеблется в зависимости от изменения стрел провеса и натяжения контактных проводов, и только при беспровесном положении контактных проводов она равна сумме внешних нагрузок на отдельные провода подвески.

В различных системах цепной подвески натяжения несущего троса изменяются по различным законам в зависимости от характера изменений стрел провеса контактных проводов той или иной системной подвески.

При выводе уравнения состояния цепных подвесок принимается, что нагрузки от контактного и вспомогательного проводов, а также от струн и деталей подвески распределяются равномерно по длине несущего троса; при этом концы контактных проводов жестко закреплены. Это дает возможность получить уравнение в общем виде, откуда потом легко могут быть получены расчетные формулы для любого типа цепной подвески.

Для вывода уравнения состояния цепной подвески принимаются следующие обозначения:

l — длина пролета, м;

g — нагрузка от веса проводов цепной подвески, кг/пог. м;

q — результирующая нагрузка несущего троса, кг/пог. м;

Т — горизонтальная составляющая натяжения несущего троса, кг;

К — сумма натяжений контактных проводов (в двойной цепной подвеске также и вспомогательного провода), кг;

F — стрела провеса несущего троса, м;

f _к — стрела провеса контактных проводов, м;

Е — модуль упругости несущего троса, кг/мм

S — сечение несущего троса, мм 2 ;

α — температурный коэффициент линейного расширения материала несущего троса;

t — температура окружающего воздуха, °С.

Величины Т, К, F , q и t с индексом «1» относятся к исходному режиму, с индексом «х» – к определяемому режиму и с индексом «0» — к режиму беспровесного положения контактного провода.

Рассмотрим условия равновесия половины пролета цепной подвески (рис. 3.29). Пусть несущий трос имеет произвольную стрелу провеса F , не равную стреле провеса троса F ₀ при беспровесном положении контактного провода. Контактный провод получит при этом стрелу провеса f _к . Обозначим отношение f _к /( F — F ₀ ) через φ и назовем его конструктивным коэффициентом цепной подвески, тогда

(3.38)

Рис. 3.29. Схема для расчета натяжений несущего троса цепной подвески

Приравнивая к нулю сумму моментов всех сил относительно точки А, получаем

откуда после приведения подобных членов и замены f _к его выражением (3.83) находим

(3.84)

Так как при беспровесном положении контактного провода несущий трос можно рассматривать как свободно подвешенный провод, находящийся под действием нагрузки от собственной массы проводов цепной подвески, то значение F ₀ можем определить по формуле

(3.85)

Подставив это значение F ₀ в уравнение (3.84), получим:

(3.86)

(3.87)

Тогда выражение стрелы провеса несущего троса примет вид

(3.89)

Величину W , имеющую размерность кг/пог. м, будем называть приведенной нагрузкой цепной подвески, величину Z — соответственно приведенным натяжением (при φ = 1 величина Z равна сумме натяжений всех проводов цепной подвески).

Введение этих подстановок позволяет значительно упростить расчетные формулы цепной подвески и привести их к виду, подобному расчетным формулам простой подвески.

Для вывода зависимости натяжения несущего троса от температуры и нагрузки определим значения удлинений несущего троса при переходе от одного режима температуры и нагрузки к другому. Пусть известно, что при температуре t ₁ и нагрузке q ₁ несущий трос имеет натяжение Т₁ и стрелу провеса F ₁ . Обозначим через T_x и F_x натяжение и стрелу провеса несущего троса при изменившихся температуре t_x и нагрузке q_x .

При изменении стрелы провеса троса от значения F ₁ до значения F_x величину полного удлинения троса в пролете l можем определить согласно (3.23) через

(3.90)

Так как полное удлинение троса составляется из упругого и температурного удлинений, можем приравнять выражение (3.90) сумме этих удлинений и получить уравнение

Заменив в этом уравнении F_x и F ₁ их значениями из выражения (3.89) и разделив обе части уравнения на l , находим

(3.91)

Левая часть этого уравнения представляет собой полное относительное удлинение несущего троса при переходе от одного режима температуры и нагрузки к другому, правая – сумму соответствующих упругого и температурного относительных удлинений. Величины W и Z в этом уравнении имеют следующие значения:

В случае полукомпенсированной цепной подвески К = со nst , вследствие чего Т _x — T ₁ = Z_x — Z ₁ и уравнение (3.91) принимает вид, полностью подобный уравнению для расчета простой подвески.

Для решения уравнения (3.91) приведем его к виду

Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Выделив в квадратные скобки члены, имеющие постоянное значение, получим

(3.92)

Величина коэффициента φ, входящего в выражения W и Z , определяется конструкцией и размещением струн вблизи опорного узла цепной подвески рассматриваемого типа цепной подвески.

В применявшейся до последнего времени методике расчета цепных подвесок значение конструктивного коэффициента цепной подвески φ принималось постоянным и равным

(3.93)

где с — расстояние от опор до ближайших к ним простых (нерессорных) струн.

В действительности, как показал Ю. В. Флинк, значение конструктивного коэффициента φ непостоянно и изменяется в определенных пределах в зависимости от изменения натяжений несущего троса и контактного провода.

При расположении простых струн на расстоянии с от опор положение контактного провода в пролете может быть представлено схемой (рис. 3.30). Рассматривая отдельно среднюю часть пролета длиной 1— 2с, ограниченную струнами СЕ и DF и учитывая, что при имеющемся расположении струн в этой части пролета φ = 1, видим, что стрелу провеса контактного провода можно определить выражением

Подставляя найденное значение f_x в выражение (3.83) и определяя согласно (3.85) и (3.86) значения F_x и F ₀ получим

откуда после преобразований

Решая это уравнение относительно φ _x , находим

(3.94)

Рис. 3.30. Схема расположения проводов цепной подвески при смещенных относительно опор струнах

Из выражения (3.94), полученного А. В. Фрайфельдом, видно, что величина φ_х зависит не только от конструктивных параметров цепной подвески, но и также от значений натяжения несущего троса и контактного провода.

Сравнительные расчеты, однако, показывают, что введение переменного значения φ_х, значительно усложняющее расчет натяжений и стрел провеса несущего троса, не вносит существенных коррективов в их значения. Поэтому при расчетах натяжений и стрел провеса несущего троса можно без существенных погрешностей принимать φ постоянным – соответствующим среднему значению К_х/Т_х . При этом для полукомпенсированной цепной подвески К = со nst и среднее значение T_x можно принимать равным Т _x =0,7 T_max , для компенсированной цепной подвески К = со nst и Т = со nst , поэтому φ постоянно и зависит только от конструктивных параметров цепной подвески.

При значениях φ

Для расчета полукомпенсированной цепной подвески, где К = со nst и Т_х – Т₁ = Z_x – Z ₁ , уравнение (3.91) может быть приведено к виду

(3.95)

(3.96)

Для расчета некомпенсированных цепных подвесок, где Т_х= Z _х -φК_х и Т₁= Z ₁ -φК₁, уравнение (3.91) приводится к виду

(3.97)

Для решения этого уравнения и построения кривой Т_х = f ( t_x ) необходимо предварительно определить зависимость K _х = f ( t_x ).

Натяжения контактного провода можно определить по форму лам простой подвески, полагая l равным среднему расстоянию между струнами. Так как это расстояние невелико, можно для упрощения расчета принять, что провод подвешен на бесконечно большом числе струн, пренебрегая, таким образом, влиянием стрел провеса контактного провода на величину его натяжения.

Если контактный провод имеет по концам постоянное закрепление (не компенсирован), то можно считать, что длина его остается неизменной, т.е. сумма температурных и упругих удлинений контактного провода равна нулю. Отсюда легко могут быть найдены величины натяжений контактного провода К при некомпенсированной подвеске. Для этого обозначим:

Е_к — модуль упругости контактного провода, кг/мм 2 ;

α_к — температурный коэффициент линейного расширения матери ала контактного провода;

S _к – сечение контактного провода, мм 2 .

(3.98)

Полагая что t _к и t_min и K ₁ = K_max , получим

В случае применения сезонного регулирования натяжения контактных проводов формула (3.98) дает значения натяжений лишь для зимнего периода. В летний период величина натяжения провода будет определяться по этой же формуле, но t_min – температура, при которой для летнего периода регулировки контактному проводу дается наибольшее допускаемое натяжение.

При полукомпенсированной цепной подвеске К= со nst .

При двойной цепной подвеске величины К_х и К₁ представляю собой значения суммы натяжений вспомогательного и контактных проводов при соответствующих режимах, для определения этих значений необходимо произвести также механический расчет вспомогательного провода. При компенсированных вспомогательном и контактных проводах значение К остается постоянным

Во все написанные выше виды уравнений для определения натяжений несущего троса входят приведенные нагрузки W и приведенные натяжения Z , значения которых определяются входящей в них величиной Т₀ – натяжения несущего троса при режиме беспровесного положения контактных проводов,

Величину Т₀ можно определить из уравнения (3.91). Для этого величины с индексом «1» в уравнении (3.91) следует отнести к исходному режиму, при котором Т₁ = T_max (наибольшему допускаемому натяжению), а величины с индексом «х» – к режиму беспровесного положения контактного провода, т. е. принять t_x = t ₀ и Т _x = Т₀.

Величины Z и W получат при этом следующие значения:

Если значение К₁ определено заранее (в случае некомпенсированной цепной подвески), то после указанных подстановок в уравнении окажется только одно неизвестное — Т₀.

После соответствующих преобразований уравнение приводится к виду

(3.99)

Проще определить значение Т₀ непосредственно из уравнения (3.92). Для этого, заменив в уравнении величины Z и W указанными выше значениями и приняв Т₁ = Т _max и T_x = T ₀ , подставим в правой части уравнения вместо Т₀ произвольную величину, близкую к ожидаемому при этом режиме значению натяжения троса, после чего определим соответствующее значение t_x , которое получится в общем случае неравным принятому значению t ₀ . Подставив затем другое значение Т₀ и определив соответствующее значение t_x можно вычислить действительное значение Т₀ интерполяцией. Значения Т₀ при подстановке нужно выбирать таким образом, чтобы t_x получа лось в одном случае больше, а в другом случае меньше t ₀ .

После того как определены все величины, входящие в выражения Z и W можно определить зависимость

пользуясь уравнением (3.92), после чего по формуле (3.89) могут быть найдены соответствующие значения стрел провеса несущего троса.

Так как в уравнения (3.91) и (3.92) входят значения температуры t ₁ и результирующей нагрузки q ₁ , при которых натяжение несущего троса Т₁ = Т _m _ах , то для решения этих уравнений и определения величины Т₀ необходимо предварительно оценить, какой из расчетных режимов – режим наинизшей температуры или гололедный — надо принять за исходный.

Критическая нагрузка и эквивалентный пролет цепной подвески. Исходным расчетным режимом для цепной подвески, т. е. тем режимом, при котором натяжение в несущем тросе получается наибольшим, может быть или режим наинизшей температуры, или режим наибольшей дополнительной нагрузки. Установить, какой из двух режимов следует принять за исходный, можно посредством определения критической нагрузки, которой называют такую результирующую нагрузку, когда натяжение несущего троса равно наибольшему допустимому его значению и при минимальной температуре, и при наибольшей дополнительной нагрузке. Если значение результирующей нагрузки при наибольшей дополнительной нагрузке от гололеда и ветра больше критической нагрузки, то исходным будет режим наибольшей дополнительной нагрузки (гололедный режим), в противном случае исходным будет режим наинизшей температуры.

Значение критической нагрузки q_x для расчетного пролета l определяется из уравнения (3.91), если данные с индексом «х» отнести к гололедному режиму, а с индексом «1» — к режиму наинизшей температуры.

Так как в данном случае согласно определению понятия «критическая нагрузка» Т_г = T_min = T_max , то уравнение (3.91) примет вид:

(3.100)

Определив из этого уравнения значение критической нагрузки q _к , получим

(3.101)

Для полукомпенсированной цепной подвески при К= со nst :

поэтому выражение (3.101) принимает вид

(3.102)

При определении значения g _к по формуле (3.102) можно принять

Для длин пролетов, применяемых в контактных сетях железных дорог, с достаточной степенью точности можно считать:

— при медном несущем тросе Т₀=0,75 Т _m _ах ;

— при стальном и биметаллическом сталемедном несущем тросе Т₀ = 0,8Т _max .

При этом ошибка в определении значения критической нагрузки не превосходит ±2%, что вполне достаточно для практичес ких расчетов.

Для определения величины эквивалентного пролета некомпенсированной или полукомпенсированной цепной подвески применимы те же рассуждения которые были приведены для простой подвески.

Удлинение несущего троса в пролете длиной l _i при переходе от режима с индексом «1» к режиму с индексом «х» согласно выражениям (3.89) и (3.90) получится равным

Принимая, что конструктивный коэффициент цепной подвески φ, а следовательно, и значения приведенной нагрузки W_x и W ₁ остаются одними и теми же во всех пролетах анкерного участка, и суммируя удлинения Δ L во всех пролетах, получим уравнение

Разделив это выражение на , найдем относительное удлинение несущего троса в данном анкерном участке:

Приравнивая это относительное удлинение к сумме упругого и температурного относительных удлинений несущего троса, будем иметь

(3.103)

Видео:Общее устройство подвески автомобиля. 3D анимация.Скачать

Так как в эквивалентном пролете согласно его определению значения натяжений несущего троса должны изменяться по тому же закону, что и на рассматриваемом анкерном участке, то для эквивалентного пролета l _э может быть написано следующее уравнение:

(3.104)

Приравнивая левые части выражений (3.103) и (3.104), получим

(3.105)

Таким образом, для цепной подвески, имеющей однотипную конструкцию во всех пролетах анкерного участка, величина эквивалентного пролета определяется той же формулой, что и для свободно подвешенного провода.

В тех случаях, когда величины пролетов анкерного участка не значительно отличаются друг от друга, эквивалентный пролет, определяемый по формуле (3.105), получается близким к среднему арифметическому значению пролета для данного анкерного участка и без ущерба для точности расчета может быть заменен этим значением.

Расчет натяжения несущего ненагруженного троса. Кроме значений натяжения несущего троса цепной подвески в нагруженном его состоянии иногда бывает необходимо знать также величины натяжений ненагруженного несущего троса, т. е. значения тех натяжений, которые должен иметь несущий трос при его монтаже до подвески на нем контактных проводов.

Натяжение ненагруженного несущего троса можно определить по формуле простой подвески, приняв в качестве исходного режима режим загрузки несущего троса контактными проводами при температуре t ₀ и беспровесном их положении. Для этого обозначим:

Т₀ — натяжение нагруженного несущего троса при температуре t ₀ беспровесного положения контактных проводов, м;

H_x — определяемое натяжение ненагруженного троса при температуре t_x ;

g ₀ — нагрузка от собственного веса цепной подвески;

g _т — нагрузка от собственного веса несущего троса.

После подстановки этих значений получим

(3.106)

Подставляя в полученное уравнение различные значения Н_х, взятые через произвольные интервалы, определяем соответствующие значения t_x и строим кривую Н _x = f ( t_x ).

Соответствующие величины стрел провеса вычисляют по формуле

(3.107)

Если при монтаже цепной подвески подвешивают только один контактный провод, но в дальнейшем предусматривается возможность подвески второго, то сначала определяют натяжение несущего троса с двумя контактными проводами по формуле (3.106), а затем рассчитывают его натяжение при одном контактном проводе в режиме беспровесного положения контактных проводов.

Т₀₁ – натяжение несущего троса при одном контактном проводе при температуре беспровесного положения контактного провода;

Т₀₂ — натяжение несущего троса, нагруженного двумя контактными проводами, при температуре беспровесного положения контактных проводов;

g ₁ — нагрузка от собственного веса цепной подвески при одном контактном проводе.

g ₂ — нагрузка от собственного веса цепной подвески при двух контактных проводах;

Тогда, применяя формулу простой подвески (3.4 1), можно написать

(3.108)

Определив из полученного выражения Т₀₁, можно найти зависимость Т_х= f ( t_x ) для подвески с одним контактным проводом, пользуясь формулой (3.92) и принимая в качестве исходного режим беспровесного положения контактного провода.

После введения принятых обозначений уравнение (3.92) получит вид:

Подставив вместо W ₀₁ и Z ₀₁ их значения

и сократив числитель и знаменатель второго члена в квадратных скобках на Т₀₁+φК₀₁, получим

(3.109)

После определения значений T_x ₁ величины стрел провеса несущего троса с одним контактным проводом могут быть определены по формуле

(3.110)

Расчет стрел провеса и изменений высоты контактных проводов и определение длин струн цепной подвески. Стрелы провеса f_x контактных проводов цепной подвески определяются по формуле

(3.111)

где F_x и F ₀ – стрелы провеса несущего троса в рассматриваемом пролете при расчетном режиме и при температуре расчетного беспровесного положения контактных проводов;

φ_х – конструктивный коэффициент цепной подвески, определяемый по формуле (3.94).

Изменения высоты контактных проводов одинарной цепной подвески в середине рассматриваемого пролета рассчитывают по формуле

(3.112)

а под ближайшей от опоры простой (нерессорной) струной – из выражения

(3.113)

Определение длин струн производим для общего случая, когда высота цепной подвески у опор, ограничивающих данный пролет, различны (рис. 3.31).

Рис. 3.31. Схема для расчета длины струны цепной подвески

Рассмотрим цепную подвеску при режиме беспровесного положения контактных проводов. Принимая, что несущий трос располагается по параболе, ось абсцисс совпадает с контактным проводом, а ось ординат – с осью левой опоры, получим уравнение несущего троса в виде

(3.114)

где y = h – высота искомой струны.

Значение свободного члена В определяем из условия, что при х = 0 y = h ₁ . Тогда

Значение коэффициента А можно определить из условия, что при х = l , у = h ₂ . Тогда

и уравнение (3.114) примет вид:

(3.115)

При h ₁ – h ₂ уравнение получит вид

(3.116)

В этом случае пролет получается симметричным относительно его середины, и струны, находящиеся на одинаковых расстояниях от опор, получаются равными.

Для определения минимальной длины нескользящей струны длиной С, находящейся на расстоянии L от средней анкеровки, угол наклона к вертикали определяется из выражения

где Δ L — продольное смещение нижнего конца струны от среднего положения.

Нескользящие струны могут применяться при угле наклона φ не более 30 0 , в этом случае Sinφ =0,5 и выражение примет вид

где С _min — минимальная длина нескользящей струны; (Δ L ) _m _ах – наибольшая величина температурного смещения контактного провода в точке, расположенной на расстоянии L от средней анкеровки. Величина (Δ L ) _m _ах может быть определена приблизительно (без учета влияния изменений упругих деформаций контактного провода и перемещений, вызываемых изменениями стрел его провеса) из выражения

где (Δ t ) _max – наибольшая величина изменения температуры, (среднего ее значения);

α_к — коэффициент температурного расширения материала контактного провода.

Подставляя значение (Δ L ) _m _ах в выражение для С _min , получим

Расчет рессорной цепной подвески . Определение натяжений и стрел провеса несущего троса рессорной цепной подвески производится по общим формулам (3.91) и (3.92). Определение изменений высоты контактных проводов в середине пролета и у ближайших от опор нерессорных струн производится по формулам (3.112) и (3.113).

Таким образом, при расчете рессорной цепной подвески не обходимо дополнительно выяснить лишь изменения, происходящие в опорном узле цепной подвески, которые определяются принятыми параметрами рессорного провода.

Рассмотрим опорный узел рессорной цепной подвески (рис. 3.32), где сплошными линиями показано положение проводов при температуре t ₀ и штриховыми — при температуре t_x .

Стрела провеса несущего троса в точке крепления к нему рессорного провода при температуре t ₀ определяется выражением:

Видео:Подвеска | Science Garage На РусскомСкачать

Для расчета стрелы провеса ψ₀ рессорного провода при температуре t ₀ примем длину вертикальной части рессорной струны С не менее принятой минимальной длины струны С _min . Отсюда получим (см. рис. 3.32)

(3.117)

Рис. 3.32. Схема изменения положения проводов в подопорном узле рессорной цепной подвески: 1 — несущий трос; 2 — рессорный трос; З — рессорная струна; 4— контактный провод

Расстояние b ₀ от точки крепления несущего троса у опоры до нижней точки рессорного провода определяется из выражения b ₀ = у₀+ψ₀.

При изменении температуры величины y ₀ , ψ₀ и b ₀ изменяются и получают при температуре t_x значения y_x , ψ _x и b_x .

Величина y_x определяется на основании результатов расчета натяжения несущего троса по формуле

(3.118)

Значения ψ _x определяются отдельным расчетом, учитывая изменения длины ветвей рессорного провода, вызванные изменением температуры. При этом для упрощения расчета упругими изменениями длины рессорного провода пренебрегаем вследствие малого его натяжения и, кроме того, полагаем, что точки А и А’ находятся на одной вертикали.

Длину ветви АВ рессорного провода при температуре t ₀ находим из треугольника АВС:

При изменении температуры на величину ( t_x — t ₀ ) ветвь АВ займет положение А’В’, причем длина ее будет равна

Зная величину А’В’, определим из треугольника А / В / С / величину ψ _x

после преобразования получим

(3.119)

Зная у_х и ψ _x можем определить изменения высоты контактных проводов под опорой по формуле

(3.120)

Как видно из полученных формул (3.118) – (3.120), для определения значений у_х, ψ_х и b_x необходимо предварительно определить параметры рессорной струны: ψ₀ – стрелу провеса рессорного провода при температуре t ₀ и а расстояние от опоры до точки закрепления рессорного провода на несущем тросе.

Величина ψ₀ ограничивается габаритными условиями цепной подвески и рассчитывается по формуле (3.117). Значения а и φ могут быть определены путем ряда пробных подсчетов при условии, что изменения высоты контактного провода под опорой при крайних температурных режимах должны получаться примерно такими же, как под ближайшими от опор простыми струнами, и что значения эластичности контактной подвески под опорами и под ближайшими от них простыми струнами будут примерно одинаковыми.

Расчет двойной цепной подвески. Натяжения и стрелы провеса несущего троса двойной цепной подвески определяются по уравнению (3.92), причем величина К в выражениях Z и W , входящих в это уравнение, принимается равной сумме натяжений вспомогательного и контактных проводов при соответствующих значениях температуры.

При определении значения коэффициента φ для схемы двойной подвески (рис. 3.33), величина с берется равной а.

В том случае, если вспомогательный провод не компенсирован, величины его натяжений и стрел провеса в зависимости от температуры определяются предварительно отдельным расчетом.

Вспомогательный провод рассчитывается как гибкая пить, подверженная действию двух равных сосредоточенных нагрузок (рис. 3.34), значения которых определяются выражениями:

при двух контактных проводах

при одном контактном проводе

где g _к — масса 1 пог. м контактного провода;

g_u – масса 1 пог. м вспомогательного провода;

g_c — масса между вспомогательным и контактным проводами;

а — расстояние между струнами контактных проводов.

Рис. 3.33. Схема двойной цепной подвески: 1 — вспомогательный трос; 2 — контактный провод; 3 — струна; 4 — несущий трос

Рис. 3.34. Схема для расчета вспомогательного провода двойной цепной подвески

U_x и U ₁ — натяжение вспомогательного провода при определяемом и исходном режимах;

ψ_х и ψ₁ — стрелы провеса вспомогательного провода при определяемом и исходном режимах;

t_x и t ₁ – температура определяемого и исходного режимов;

α_u , E_u , S_u — температурный коэффициент линейного расширения, модуль упругости и сечение вспомогательного провода.

Величина удлинения Δ L вспомогательного провода в пролете длиной l =2а при изменении натяжения провода на ( U_x — U ₁ ) и температуры на ( t_x — t ₁ ) определяется по выражению:

(3.121)

То же удлинение вспомогательного провода можно определить из геометрических соотношений в зависимости от изменения стрелы провеса ψ.

Полная длина провода при стреле провеса ψ_х определяется (см. рис. 3.34) по выражению

(3.122)

Приравнивая нулю сумму моментов сил, приложенных влево от точки А (точки приложения сосредоточенной силы Р_х), получим

(3.123)

Подставляя полученное значение ψ_х в выражение (3.122), получим

(3.124)

Заменяя корень в выражении (3.124) его приближенным значением

(3.125)

Таким же образом получим значение длины провода L ₁ при стреле провеса ψ₁ и натяжении U ₁ :

(3.126)

Удлинение провода Δ L определится разностью выражений (3.125) и (3.126):

(3.127)

Приравнивая правые части выражений (3.121) и (3.127) и сокращая на 2 а, получим

Это уравнение может быть приведено к виду

Отсюда, задаваясь значением U ₁ — натяжением вспомогательного провода при исходном режиме t ₁ , можем определить зависимость U_x = f ( t_x ).

Значения стрел провеса ψ _x вспомогательного провода определяются из выражения (3.123).

Изменения высоты контактных проводов в середине пролета при двойной цепной подвеске находят по формуле

(3.129)

а изменения под ближайшей от опоры струной цепной подвески — по формуле

(3.130)

где F_x и F ₀ — стрелы провеса несущего троса;

ψ _x и ψ₀ — стрелы провеса вспомогательного провода при определяемом режиме и при режиме расчетного беспровесного положения контактных проводов;

φ _x — конструктивный коэффициент цепной подвески, определяемый по формуле (3.94).

Изменения высоты контактных проводов под опорой Δ h_Bx могут быть приняты равными Δ h_Ax .

В том случае, если вспомогательный провод компенсирован, следовательно

выражения (3.129) и (3.130) принимают вид

Видео:Чем отличается подвеска Макферсон от многорычажной, и какие автомобильные подвески бываютСкачать

В заключение следует отметить, что методы расчетов цепных подвесок (натяжений, стрел провеса) продолжают совершенствоваться как в России, так и за рубежом. Расчеты для полностью компенсированных подвесок значительно упрощаются. Конечное число струн (между первыми нерессорными) учитывается в методиках Уральского государственного университета путей сообщения (А.В. Ефимов, А.Г. Галкин). Широко используются возможности расчета на ЭВМ.