Конспект урока
Геометрия, 11 класс
Урок №8. Сфера и шар
Перечень вопросов, рассматриваемых в теме:
- что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
- что такое шар и его элементы;
- уравнение сферы;
- формула для нахождения площади поверхности сферы;
- взаимное расположение сферы и плоскости;
- теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.
Глоссарий по теме:
Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.
Круг – это часть плоскости, ограниченная окружностью.
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.
Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Основные теоретические факты
По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.
Рисунок 1 – Сфера с центром в точке О и радиусом R
Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.
Сферу можно получить ещё одним способом — вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.
2. Уравнение сферы
Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.
Пусть сфера имеет центром точку С (x0; y0; z0) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:
МС=
Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС 2 =R 2 , то есть координаты точки М удовлетворяют уравнению:

Это выражение называют уравнением сферы радиуса R и центром С(x0; y0; z0).
3. Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.
1. Пусть d
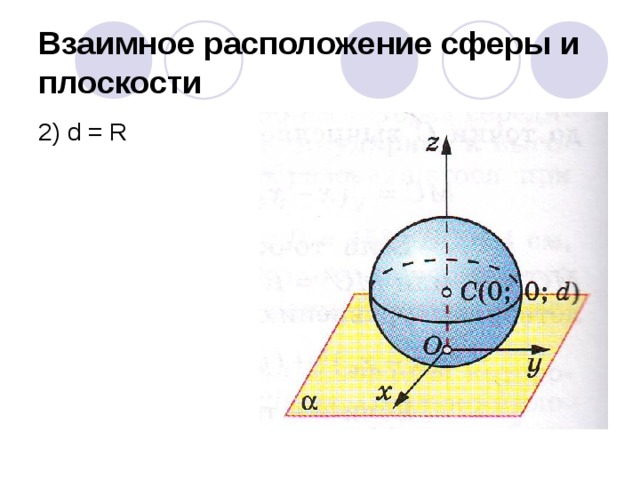
2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.
3. Пусть d
Рассмотрим случай касания более подробно.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Теорема (свойство касательной плоскости).
Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема (признак касательной плоскости):
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.
4. Основные формулы
Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:
Формула для вычисления площади поверхности сферы и ее элементов:
S=4πR 2 – площадь сферы.
S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

Примеры и разбор решения заданий тренировочного модуля
1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.
Площадь круга вычисляется по формуле: Sкр=πR 2 .
Площадь поверхности шара вычисляется по формуле: Sсф=4πR 2 . Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.
2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.
Площадь сферы равна Sсф=4πR 2 . То есть Sсф=100π.
По условию площадь круга некоторого радиуса r также равна 100π. Значит, r 2 =100, то есть r=10.
3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15
Окружность, вписанная в треугольник, является сечением сферы.
Найдем ее радиус.
Площадь треугольника с известными сторонами можно вычислить по формуле Герона:
С другой стороны, S=p·r.
Теперь найдем расстояние от центра шара до секущей плоскости.
4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.
Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.
Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.
Видео:11 класс, 21 урок, Взаимное расположение сферы и плоскостиСкачать

Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости
Урок геометрии в 11 классе
Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости
Просмотр содержимого документа
«Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости»
Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости.
- Окружность – множество точек плоскости, равноудаленных от данной точки
- Точка О – центр окружности
- ОА — радиус
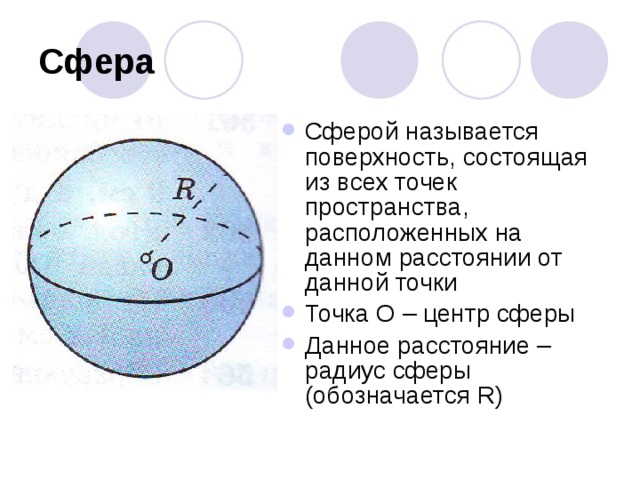
- Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки
- Точка О – центр сферы
- Данное расстояние – радиус сферы (обозначается R)
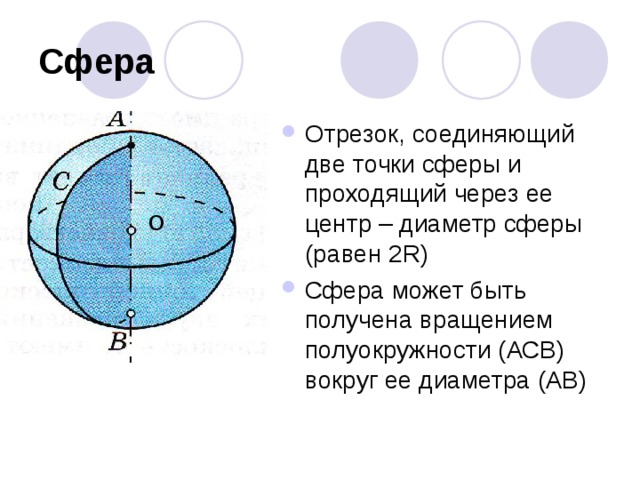
- Отрезок, соединяющий две точки сферы и проходящий через ее центр – диаметр сферы (равен 2 R )
- Сфера может быть получена вращением полуокружности (АСВ) вокруг ее диаметра (АВ)
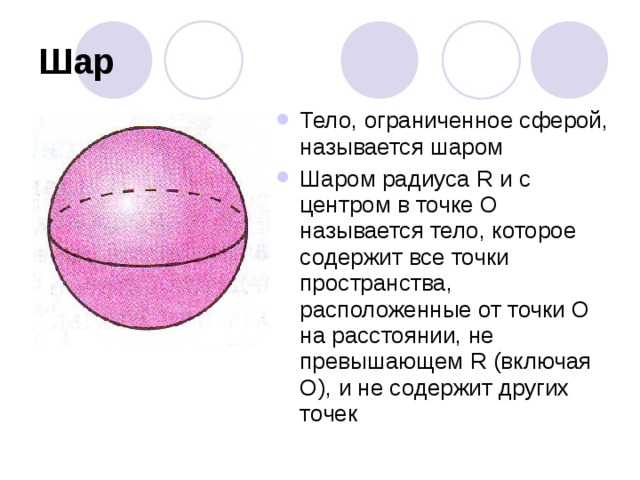
- Тело, ограниченное сферой, называется шаром
- Шаром радиуса R и с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек
- Пусть R – радиус сферы
- С(х˳,у˳, z ˳) – центр окружности
- Расстояние от произвольной
точки М(х,у, z ) до точки С найдем
Если точка М лежит на данной сфере,
Координаты точки М удовлетворяют
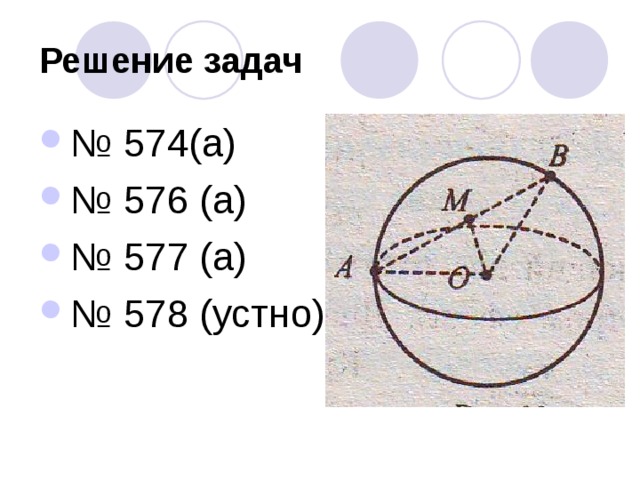
- № 574(а)
- № 576 (а)
- № 577 (а)
- № 578 (устно)
Взаимное расположение сферы и плоскости
- R – радиус сферы
- d – расстояние от центра до плоскости α
- Плоскость Оху совпадает с плоскостью α , поэтому ее уравнение имеет вид z=0
- Центр сферы С лежит на положительной полуоси О z , т.е. имеет координаты С(0;0; d)
- Уравнение сферы
Взаимное расположение сферы и плоскости
Если координаты произвольной точки М (х;у; z) удовлетворяют обоим уравнениям, то М лежит как в плоскости α , так и на сфере.
Вопрос о взаимном расположении сводится к исследованию системы уравнений
Подставив z = 0 во второе уравнение, получим
Взаимное расположение сферы и плоскости
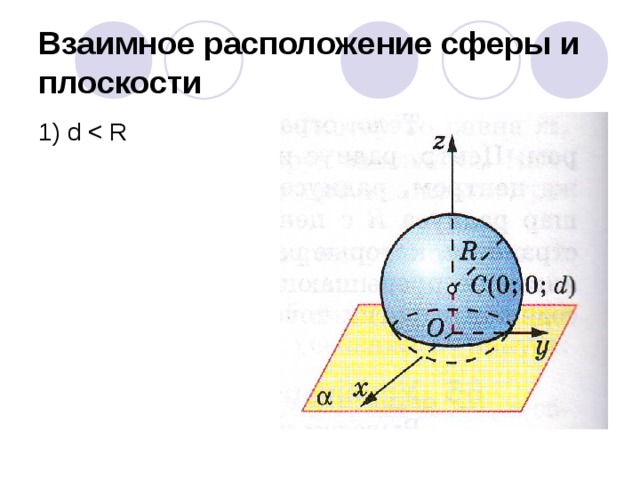
1) d
Взаимное расположение сферы и плоскости
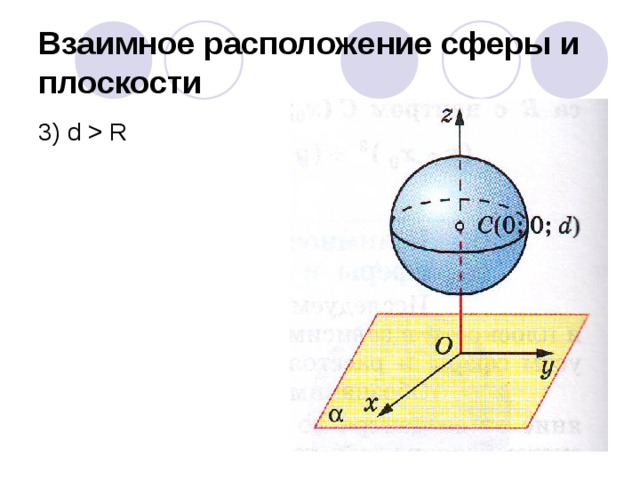
Взаимное расположение сферы и плоскости
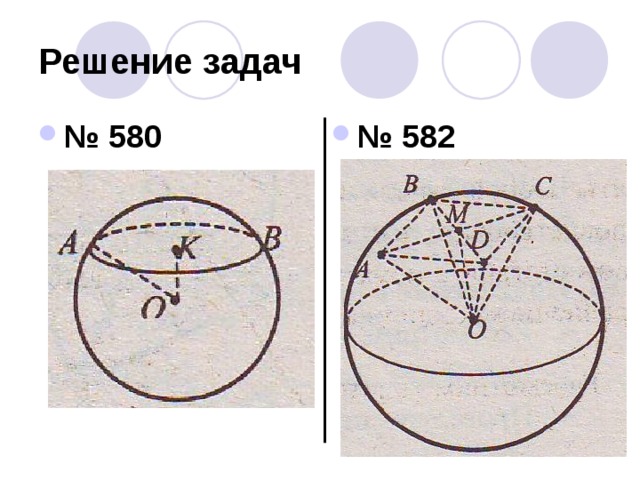
- №580
- №582
Видео:11 класс, 20 урок, Уравнение сферыСкачать

Взаимное расположение сферы и плоскости в пространстве
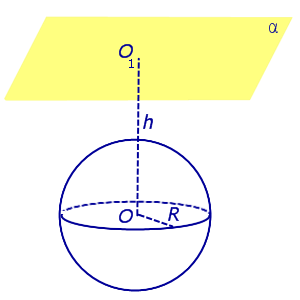
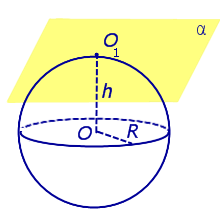
Рассмотрим сферу радиуса R с центром в точке O и плоскость α . Обозначим символом O 1 основание перпендикуляра, опущенного из точки O на плоскость α , и обозначим буквой h расстояние от точки O до плоскости расстояние от точки O до плоскости α (т. е. длину отрезка OO1 ).
В зависимости от соотношения между R и h можно составить следующую таблицу, в которой описаны все возможные случаи взаимного расположения сферы и плоскости в пространстве .
| Взаимное расположение фигур | Рисунок | Свойства | ||
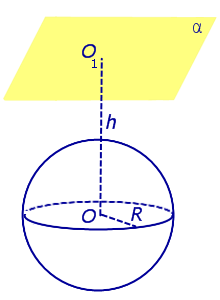
| Сфера и плоскость не имеют общих точек (не пересекаются) | ||||
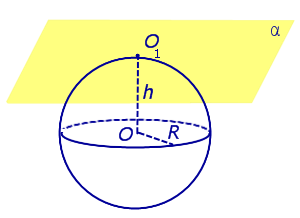
| Сфера и плоскость имеют единственную общую точку (касаются) | ||||
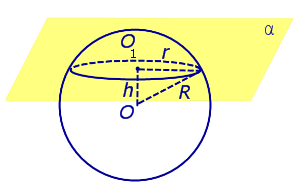
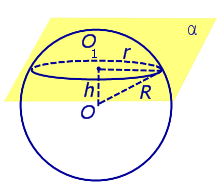
| Сфера и плоскость имеют более одной общей точки. Плоскость не проходит через центр сферы. | ||||
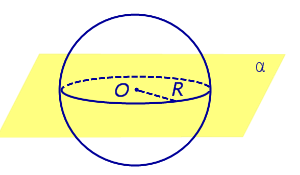
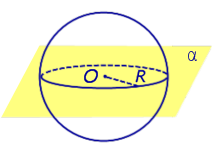
| Сфера и плоскость имеют более одной общей точки. Плоскость проходит через центр сферы. |
| Сфера и плоскость не имеют общих точек (не пересекаются) |
| Сфера и плоскость имеют единственную общую точку (касаются) |
| Сфера и плоскость имеют более одной общей точки. Плоскость не проходит через центр сферы. |
| Сфера и плоскость имеют более одной общей точки. Плоскость проходит через центр сферы. |