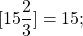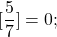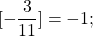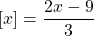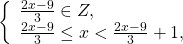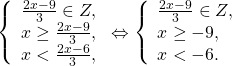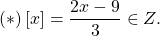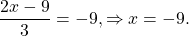Уравнения с целыми частями график

Построение графиков целой и дробной части числа

Рассмотрим интересный вид кусочно-заданных функций.

`[x] = n` при `n

Поэтому график этой функции имеет следующий вид (рис. 16).

Рассмотрим более трудный пример.

Построить график функции f ( x ) = [ 2 x + 3,5 ] f(x) = [2x + 3,5] .

Ясно, что [ 2 x + 3,5 ] = [ 2 x + 0,5 ] + 3 [2x + 3,5]= [2x + 0,5] + 3 . Далее,

из определения целой части числа следует такое представление:

Видео:7 класс, 35 урок, Графическое решение уравненийСкачать

Урок-семинар по теме: «Решение уравнений, содержащих целую часть числа»

Разделы: Математика

Цель урока.

• Углубление знаний по теме урока.
• Развитие самостоятельной учебно-познавательной деятельности.
• Развитие навыков групповой работы.
• Оценка реальности и красоты каждого из предложенных способов решения уравнения.

Тип урока: комбинированный.

Метод: проблемный и частично поисковый.

Оборудование:

• Кодоскоп.
• Плёнки с графиками функций ;
• “Информация к размышлению”- подборка задач по теме “целая и дробная части числа” для учащихся 8-11-х классов с указанием литературы.

Предварительная подготовка к уроку-семинару.

Класс разбивается на 4 группы (по числу способов решения уравнения), для каждой группы указывается способ решения и литература, где этот способ можно найти. Затем для каждой группы производится консультация, на которой проверяется готовность каждой группы и выясняются все возникающие вопросы. Каждая группа выдвигает своего докладчика, который будет на уроке решать задачу указанным способом.

План урока:

1. Организационный момент.
2. Вступительное слово учителя.
3. Повторение.
4. Проверка домашнего задания.
5. Семинар.
6. Итог урока.

Вступительное слово учителя.

В последние годы задачи на решение уравнений с целой частью числа постоянно встречаются на олимпиадах и на вступительных экзаменах в высшие учебные заведения. Такие задачи для учеников являются непривычными и сложными.

Впервые знакомство с целой и дробной частью числа встречается в 8-м классе, когда вводится определение целой и дробной части числа и строятся графики y=[x]; y=;

Но в учебниках нет методов решения уравнений, содержащих целую часть числа.

Поэтому сегодня мы повторим то, что знаем и рассмотрим различные способы решения ещё одного вида уравнений, содержащих целую часть числа.

Повторение.

Вызываю 2 человека к доске решать домашнее задание.

Устно с помощью кодоскопа:

Определение целой части числа. Найти [25,8]; [0.75]; [-1]; [-2,74]; [-3,8].

Свойства: если, то [x]=x; если то [x] 3.

При m=4 значит, промежуток [5;6) не входит в решение уравнения.

в) Получим, что данному уравнению из интервала (2;6) не удовлетворяют числа 2

0t 2) график y=[x-1] берётся из домашнего задания; 3)обе плёнки совмещаем на экране. Графики и совпадают при 3x 26.11.2003 Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать Функция целая часть числа Целой частью действительного числа x (x∈R) называется наибольшее целое число, не превосходящее x. Целую часть числа x обозначают символом [x]. [x] читают «антье от x». Обозначение [x] в 1808 году ввёл К. Гаусс. В частности, если n — целое число (n∈Z), то [n]=n. Вычислить целую часть числа: 7,8; 0,12; -0,7; -4,92; 15 2/3; 5/7; -3/11; 8; -50. Фактически вычисление целой части числа x представляет собой округление до ближайшего к числу x целого числа в меньшую сторону (то есть округление с недостатком). Функцию, ставящую в соответствие каждому значению x его целую часть — число [x], называют целой частью числа x и обозначают y=[x] . Функция целая часть числа определена для любого действительного x (x∈R). Область значений функции y=[x] — множество целых чисел (y∈Z). По определению целой части числа 18,4 Таким образом, x∈[-9;-6) и На промежутке [-9;-6) [x] принимает три значения. Подставив в равенство (*) [x]= -9, найдём x: Так как -9∈[-9;-8), то x= -9 — корень уравнения. 2. При x∈[-8;-7) [x]= -8, откуда -7,5∈[-8;-7), поэтому x= -7,5 — корень уравнения. 3. При x∈[-7;-6) [x]= -7, и -6∉[-7;-6), значит x= -6 не является корнем уравнения. 📸 Видео Как решают уравнения в России и СШАСкачать СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать Решение биквадратных уравнений. 8 класс.Скачать Графический метод решения показательных уравнений и неравенств Алгебра 10 (база)Скачать Решение уравнений, 6 классСкачать Решить уравнение с целой и дробной частьюСкачать Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать Вспоминаем схему Горнера и уравнения высших степенейСкачать Формула линейной функции по ее графикуСкачать Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать КАК РЕШАТЬ УРАВНЕНИЯ С ДРОБЯМИ И ЦЕЛЫМИ ЧИСЛАМИ? Примеры | МАТЕМАТИКА 5 классСкачать Линейное уравнение с двумя переменными. 7 класс.Скачать Дробно-рациональные уравнения. 8 класс.Скачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства