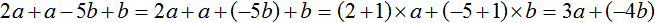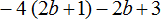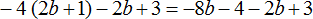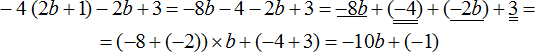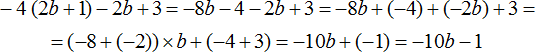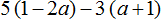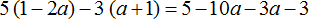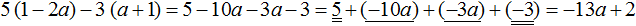Уравнения с скобками 6 класс ответами

Первый вид — обыкновенные приведенные линейные уравнения, состоящие из числовых величин и переменных с единичным степенным показателем. Они являются наиболее распространенными не только в математике и физике, но и в других дисциплинах с физико-математическим уклоном. Графиком их функции является прямая линия, которую также называют прямо пропорциональной зависимостью.

Ко второму типу относятся любые многочлены линейного типа, имеющие переменную, а также некоторый параметр. Последний влияет на решение и нахождение корней. Обычно он задается на начальном этапе решения, но бывают и исключения. В последнем случае необходимо указывать диапазон допустимых значений параметра.

Суть решения второго вида уравнений — предотвратить превращение тождества в пустое множество. Для этой цели требуется исключить при помощи записи в виде неравенства все ложные значения параметра. Выражения с параметром применяются в программировании при написании и разработке различных алгоритмов. Кроме того, их можно встретить при описании физических процессов и явлений.

Последний тип — выражения высшей степени, которые при помощи математических преобразований превращаются в первый или второй тип. Для их решения необходимо знать формулы сокращенного умножения, понижающие степень до единицы, а также навык раскрытия скобок и приведения подобных компонентов.

Обыкновенные тождества

Простое линейное уравнение записывается в таком виде: At+Bt+Ct+As+Bs+Cs=0. Некоторых коэффициентов может и не быть. Кроме того, тождество может записываться в виде выражения, включающего в свой состав скобки. Алгоритм решения имеет следующий вид:

Следует отметить, что также составляются примеры линейных уравнений для тренировки в 7 классе. Необходимо разобрать решение одного из них «7 (t-1)(t+1)-7t (t-1)=8». Решать его нужно по вышеописанному алгоритму:

Последний пункт реализации методики свидетельствует о том, что корень тождества найден правильно. Далее нужно рассмотреть выражения с параметром.

Выражения с параметром

Уравнения с некоторым параметром решаются немного по другой методике. Ее суть заключается в нахождении корня, дополнительно зависящего от некоторого значения. Алгоритм имеет следующий вид:

Реализацию методики необходимо рассмотреть на практическом примере «t-2+pt=0», где р — параметр тождества. Решать выражение нужно по такому алгоритму:

Иногда в некоторых задачах нет необходимости подставлять значение параметра. В этом случае следует просто записать формулу корня, указав допустимый интервал (диапазон) последнего. Например, в вышеописанном примере решение записывается следующим образом: t=2/(1+p)

. Каждый ученик должен понять основной смысл решения уравнений этого типа — научиться находить область значений параметра, не превращающие выражение в пустое множество.

Понижение степени

Некоторые уравнения представлены степенью при неизвестной, превышающую единицу. К ним относятся следующие виды: квадратные, кубические и бикубические. Каждый из трех видов имеет собственный алгоритм нахождения корней.

Однако некоторые из них можно свести к линейному типу. Для этого применяется метод разложения на множители. Он подразумевает алгебраические соотношения, при помощи которых выражение легко записывается в обыкновенной линейной форме. К ним относятся следующие:

Первая и вторая формула называется квадратом суммы или разности соответственно. Третья — разность квадратов. Кроме того, бывают случаи, при которых невозможно применить эти тождества. Для этого требуется выносить общий множитель за скобки, тем самым понижая степень. Для нахождения корней существует определенная методика:

Реализация алгоритма нужно проверить на практическом примере, т. е. следует решить уравнение «3t^2-3=0». Найти его корни можно, воспользовавшись вышеописанной методикой:

Кубические и бикубические должны сводиться к квадратным, а затем преобразовываться в линейные, поскольку формулы кубов суммы и разности, при их разложении на множители, дают вторую степень. Однако существует еще один частный случай, о котором не упоминалось при классификации линейных выражений с неизвестными — системы уравнений.

Системы линейного типа

Система уравнений — совокупность выражений с неизвестными, которые имеют общие решения. Методика для вычисления корней имеет следующий вид:

Однако для практического применения вышеописанной методики необходимо разобрать систему уравнений, состоящую из двух тождеств (5t-2s=1 и 4t^2-s^2=0). Решать ее нужно по вышеописанной методике:

В третьем пункте математики рекомендуют разложить тождество на множители, поскольку необходимо всегда понижать степень при неизвестной величине. Во всех трех случаях описаны простые примеры, которые позволяют перейти к более сложным заданиям.

Следует отметить, что еще одним методом решения системы уравнений считается построение графиков функций, входящих в ее состав. Методика поиска решений сводится к простым шагам, которые можно править относительно предыдущего алгоритма таким образом:

В последнем пункте методики находятся корни системы уравнений. Далее рекомендуется их подставить в исходные выражения для проверки.

Таким образом, линейные уравнения применяются в различных физико-математических дисциплинах и прикладных науках. Для их решения существуют определенные методики, позволяющие выполнить эту операцию за короткий промежуток времени и не допустить ошибок.

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Решение линейных уравнений. 6-й класс

Разделы: Математика

Класс: 6

Цели урока:

• повторить правила раскрытия скобок и приведения подобных слагаемых;
• ввести определение линейного уравнения с одним неизвестным;
• познакомить учащихся со свойствами равенств;
• научить решать линейные уравнения;
• научить решать задачи на «было − стало».

Оборудование: компьютер, проектор.

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Ход урока

I. Проверка предыдущего домашнего задания.

II. Повторение теоретического материала.

1. Как найти неизвестное слагаемое? [От суммы отнять известное слагаемое]
2. Как найти неизвестное уменьшаемое? [К вычитаемому прибавить разность]
3. Как найти неизвестное вычитаемое? [От уменьшаемого отнять разность]
4. Как найти неизвестный множитель? [Произведение разделить на известный множитель]
5. Как найти неизвестное делимое? [Делитель умножить на частное]
6. Как найти неизвестный делитель? [Делимое разделить на частное]
7. Как раскрыть скобки, перед которыми стоит знак плюс? [Опустить скобки и этот знак плюс, переписать слагаемые с теми же знаками]
8. Как раскрыть скобки, перед которыми стоит знак минус? [Опустить скобки и этот знак минус, переписать слагаемые с противоположными знаками]
9. Как выглядит распределительное свойство умножения? [(a+b)∙c=ac+bc]

III. Устные задания по слайдам.

(слайд 2, слайд 3).

1) Раскройте скобки:

3+(х+2); 3-(х+2); 3+(х-7); 3-(х-7); 3+(-х+5); 3-(-х+5); -4(-5-х); 9(; 9(; 2(7+9х); 4(2-3х); -6(9-5х); -3(1+4х).

2) Приведите подобные слагаемые:

6b-b; 9,5m+3m; a —a; m-m; -4x-x+3; 7x-6y-3x+8y.

3) Упростите выражение:

IV. Новая тема. Решение линейных уравнений.

До сегодняшнего урока мы не умели решать уравнения, в которых неизвестное находилось слева и справа от знака равенства: 3x+7=x+15. Некоторые из нас постоянно забывают правила нахождения неизвестного слагаемого, уменьшаемого, вычитаемого. Сегодня мы постараемся разрешить все эти затруднения.

Уравнение, которое можно привести к виду ax=b, где a и b − некоторые числа (a0), называется линейным уравнением с одним неизвестным.

Линейные уравнения обладают свойствами:

1. Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (стр. 229 учебника).
2. Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак (стр. 230 учебника).

Рассмотрим план решения линейного уравнения:

Какими из свойств равенств мы воспользовались для решения уравнения? (вторым)

Рассмотрим примеры уравнений, при решении которых будет удобно воспользоваться и первым свойством.

х+3=х+5 │∙9 Удобно умножить на наименьшее общее кратное знаменателей дробей.

(х+3)∙9=(х+5)∙9 Далее − по плану.

Видео:Как решать уравнения со скобками быстро и правильно. Математика 6 класс.Скачать

Раскрытие скобок

Продолжаем изучать основы алгебры. В данном уроке мы научимся раскрывать скобки в выражениях. Раскрыть скобки означает избавить выражение от этих скобок.

Чтобы раскрывать скобки, нужно выучить наизусть два правила. При регулярных занятиях раскрывать скобки можно с закрытыми глазами, и про те правила которые требовалось заучивать наизусть, можно благополучно забыть.

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Первое правило раскрытия скобок

Рассмотрим следующее выражение:

Значение данного выражения равно 2. Раскроем скобки в данном выражении. Раскрыть скобки означает избавиться от них, не влияя на значение выражения. То есть после избавления от скобок значение выражения 8 + (−9 + 3) по прежнему должно быть равно двум.

Первое правило раскрытия скобок выглядит следующим образом:

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Итак, мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Этот плюс нужно опустить вместе со скобками. Иными словами, скобки исчезнут вместе с плюсом, который перед ними стоял. А то, что было в скобках запишется без изменений:

Мы получили выражение без скобок 8−9+3 . Данное выражение равно 2, как и предыдущее выражение со скобками было равно 2.

Таким образом, между выражениями 8+(−9+3) и 8−9+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

8 + (−9 + 3) = 8 − 9 + 3

Пример 2. Раскрыть скобки в выражении 3 + (−1 − 4)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:

3 + (−1 − 4) = 3 − 1 − 4

Пример 3. Раскрыть скобки в выражении 2 + (−1)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:

В данном примере раскрытие скобок стало своего рода обратной операцией замене вычитания сложением. Как это понимать?

В выражении 2 − 1 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 2 + (−1) . Но если в выражении 2 + (−1) раскрыть скобки, то получится изначальное 2 − 1 .

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после каких-нибудь преобразований. То есть избавить его от скобок и сделать проще.

Чтобы упростить данное выражение, можно привести подобные слагаемые. Напомним, что для приведения подобных слагаемых, нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

Получили выражение 3a + (−4b) . В этом выражении раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок, то есть опускаем скобки вместе с плюсом, который стоит перед этими скобками:

Таким образом, выражение 2a+a−5b+b упрощается до 3a−4b .

Раскрыв одни скобки, по пути могут встретиться другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в следующем выражении:

Здесь два места, где нужно раскрыть скобки. В данном случае применимо первое правило раскрытия скобок, а именно опускание скобок вместе с плюсом, который стоит перед этими скобками:

2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6

Пример 3. Раскрыть скобки в выражении 6+(−3)+(−2)

В обоих местах, где имеются скобки, перед ними стоит плюс. Здесь опять же применяется первое правило раскрытия скобок:

6 + (−3) + (−2) = 6 − 3 − 2

Иногда первое слагаемое в скобках записано без знака. Например, в выражении 1+(2+3−4) первое слагаемое в скобках 2 записано без знака. Возникает вопрос, а какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ напрашивается сам — перед двойкой будет стоять плюс.

На самом деле даже будучи в скобках перед двойкой стоит плюс, но мы его не видим по причине того, что его не записывают. Мы уже говорили, что полная запись положительных чисел выглядит как +1, +2, +3 . Но плюсы по традиции не записывают, поэтому мы и видим привычные для нас положительные числа 1, 2, 3 .

Поэтому, чтобы раскрыть скобки в выражении 1+(2+3−4) , нужно как обычно опустить скобки вместе с плюсом, стоящим перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

1 + (2 + 3 − 4) = 1 + 2 + 3 − 4

Пример 4. Раскрыть скобки в выражении −5 + (2 − 3)

Перед скобками стоит плюс, поэтому применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед этими скобками. Но первое слагаемое, которое в скобках записываем со знаком плюс:

−5 + (2 − 3) = −5 + 2 − 3

Пример 5. Раскрыть скобки в выражении (−5)

Перед скобками стоит плюс, но он не записан по причине того, что до него не было других чисел или выражений. Наша задача убрать скобки, применив первое правило раскрытия скобок, а именно опустить скобки вместе с этим плюсом (даже если он невидим)

Пример 6. Раскрыть скобки в выражении 2a + (−6a + b)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:

Пример 7. Раскрыть скобки в выражении 5a + (−7b + 6c) + 3a + (−2d)

В данном выражении имеется два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:

Видео:Раскрытие скобок. 6 класс.Скачать

Второе правило раскрытия скобок

Теперь рассмотрим второе правило раскрытия скобок. Оно применяется тогда, когда перед скобками стоит минус.

Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный.

Например, раскроем скобки в следующем выражении

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, стоящим перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Мы получили выражение без скобок 5 + 2 + 3 . Данное выражение равно 10, как и предыдущее выражение со скобками было равно 10.

Таким образом, между выражениями 5−(−2−3) и 5+2+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

5 − (−2 − 3) = 5 + 2 + 3

Пример 2. Раскрыть скобки в выражении 6 − (−2 − 5)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок, а именно опускаем скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, записываем с противоположными знаками:

6 − (−2 − 5) = 6 + 2 + 5

Пример 3. Раскрыть скобки в выражении 2 − (7 + 3)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

2 − (7 + 3) = 2 − 7 − 3

Пример 4. Раскрыть скобки в выражении −(−3 + 4)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 5. Раскрыть скобки в выражении −(−8 − 2) + 16 + (−9 − 2)

Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить второе правило раскрытия скобок, а когда очередь доходит до выражения +(−9 − 2) нужно применить первое правило:

−(−8 − 2) + 16 + (−9 − 2) = 8 + 2 + 16 − 9 − 2

Пример 6. Раскрыть скобки в выражении −(−a − 1)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 7. Раскрыть скобки в выражении −(4a + 3)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 8. Раскрыть скобки в выражении a − (4b + 3) + 15

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 9. Раскрыть скобки в выражении 2a + (3b − b) − (3c + 5)

Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить первое правило раскрытия скобок, а когда очередь доходит до выражения −(3c+5) нужно применить второе правило:

2a + (3b − b) − (3c + 5) = 2a + 3b − b − 3c − 5

Пример 10. Раскрыть скобки в выражении −a − (−4a) + (−6b) − (−8c + 15)

Здесь три места, где нужно раскрыть скобки. Вначале нужно применить второе правило раскрытия скобок, затем первое, а затем опять второе:

−a − (−4a) + (−6b) − (−8c + 15) = −a + 4a − 6b + 8c − 15

Видео:Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Механизм раскрытия скобок

Правила раскрытия скобок, которые мы сейчас рассмотрели, основаны на распределительном законе умножения:

На самом деле раскрытием скобок называют ту процедуру, когда общий множитель умножают на каждое слагаемое в скобках. В результате такого умножения скобки исчезают. Например, раскроем скобки в выражении 3×(4+5)

3 × (4 + 5) = 3 × 4 + 3 × 5

Поэтому, если нужно умножить число на выражение в скобках (или выражение в скобках умножить на число) надо говорить раскроем скобки.

Но как связан распределительный закон умножения с правилами раскрытия скобок, которые мы рассматривали ранее?

Дело в том, что перед любыми скобками стоит общий множитель. В примере 3 × (4 + 5) общий множитель это 3 . А в примере a(b + c) общий множитель это переменная a .

Если перед скобками нет чисел или переменных, то общим множителем является 1 или −1 , в зависимости от того, какой знак стоит перед скобками. Если перед скобками стоит плюс, значит общим множителем является 1 . Если перед скобками стоит минус, значит общим множителем является −1 .

К примеру, раскроем скобки в выражении −(3b − 1) . Перед скобками стоит минус, поэтому нужно воспользоваться вторым правилом раскрытия скобок, то есть опустить скобки вместе с минусом, стоящим перед скобками. А выражение, которое было в скобках, записать с противоположными знаками:

Мы раскрыли скобки, воспользовавшись правилом раскрытия скобок. Но эти же скобки можно раскрыть, воспользовавшись распределительным законом умножения. Для этого сначала записываем перед скобками общий множитель 1, который не был записан:

Минус, который раньше стоял перед скобками относился к этой единице. Теперь можно раскрыть скобки, применяя распределительный закон умножения. Для этого общий множитель −1 нужно умножить на каждое слагаемое в скобках и полученные результаты сложить.

Для удобства заменим разность, находящуюся в скобках на сумму:

Далее умножаем общий множитель −1 на каждое слагаемое в скобках:

Как и в прошлый раз мы получили выражение −3b + 1 . Каждый согласится с тем, что в этот раз затрачено больше времени на решение столь простейшего примера. Поэтому разумнее пользоваться готовыми правилами раскрытия скобок, которые мы рассматривали в данном уроке:

Но не мешает знать, как эти правила работают.

В данном уроке мы научились ещё одному тождественному преобразованию. Вместе с раскрытием скобок, вынесением общего за скобки и приведением подобных слагаемых можно немного расширить круг решаемых задач. Например:

Раскрыть скобки и привести подобные слагаемые в следующем выражении:

Здесь нужно выполнить два действия — сначала раскрыть скобки, а потом привести подобные слагаемые. Итак, по порядку:

1) Раскрываем скобки:

2) Приводим подобные слагаемые:

В получившемся выражении −10b+(−1) можно раскрыть скобки:

Пример 2. Раскрыть скобки и привести подобные слагаемые в следующем выражении:

1) Раскроем скобки:

2) Приведем подобные слагаемые. В этот раз для экономии времени и места, не будем записывать, как коэффициенты умножаются на общую буквенную часть

Пример 3. Упростить выражение 8m+3m и найти его значение при m=−4

1) Сначала упростим выражение. Чтобы упростить выражение 8m+3m , можно вынести в нём общий множитель m за скобки:

2) Находим значение выражения m(8 + 3) при m = −4 . Для этого в выражение m(8 + 3) вместо переменной m подставляем число −4

m (8 + 3) = −4 (8 + 3) = −4 × 8 + (−4) × 3 = −32 + (−12) = −44

🎦 Видео

Решение уравнений - математика 6 классСкачать

Как решать уравнения со скобками.Как правильно раскрывать скобки.Скачать

Линейное уравнение с одной переменной. 6 класс.Скачать

Уравнения со скобками - 5 класс (примеры)Скачать

6 класс, 42 урок, Решение уравненийСкачать

Модуль числа. Практическая часть. 6 класс.Скачать

Алгебра 7 Линейное уравнение с одной переменнойСкачать

Решение простых линейных уравнений. 6 класс.Скачать

Уравнение на дроби и скобки № 72 Математика 6 классСкачать

Математика 6 класс. РАСКРЫТИЕ СКОБОК. РЕШЕНИЕ УРАВНЕНИЙ.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

дробное уравнение как решать для 6 классаСкачать