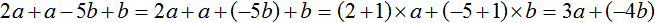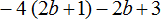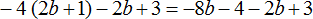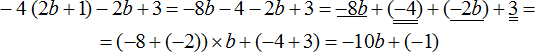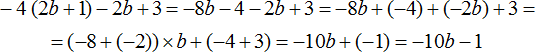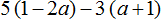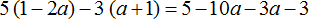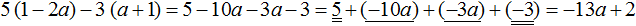Уравнения с раскрытием скобок 6 класс задания

Видео:КАК РАСКРЫТЬ СКОБКИ?Скачать

Решение линейных уравнений. 6-й класс

Разделы: Математика

Класс: 6

Цели урока:

• повторить правила раскрытия скобок и приведения подобных слагаемых;
• ввести определение линейного уравнения с одним неизвестным;
• познакомить учащихся со свойствами равенств;
• научить решать линейные уравнения;
• научить решать задачи на «было − стало».

Оборудование: компьютер, проектор.

Видео:Раскрытие скобок - математика 6 классСкачать

Ход урока

I. Проверка предыдущего домашнего задания.

II. Повторение теоретического материала.

1. Как найти неизвестное слагаемое? [От суммы отнять известное слагаемое]
2. Как найти неизвестное уменьшаемое? [К вычитаемому прибавить разность]
3. Как найти неизвестное вычитаемое? [От уменьшаемого отнять разность]
4. Как найти неизвестный множитель? [Произведение разделить на известный множитель]
5. Как найти неизвестное делимое? [Делитель умножить на частное]
6. Как найти неизвестный делитель? [Делимое разделить на частное]
7. Как раскрыть скобки, перед которыми стоит знак плюс? [Опустить скобки и этот знак плюс, переписать слагаемые с теми же знаками]
8. Как раскрыть скобки, перед которыми стоит знак минус? [Опустить скобки и этот знак минус, переписать слагаемые с противоположными знаками]
9. Как выглядит распределительное свойство умножения? [(a+b)∙c=ac+bc]

III. Устные задания по слайдам.

(слайд 2, слайд 3).

1) Раскройте скобки:

3+(х+2); 3-(х+2); 3+(х-7); 3-(х-7); 3+(-х+5); 3-(-х+5); -4(-5-х); 9(; 9(; 2(7+9х); 4(2-3х); -6(9-5х); -3(1+4х).

2) Приведите подобные слагаемые:

6b-b; 9,5m+3m; a —a; m-m; -4x-x+3; 7x-6y-3x+8y.

3) Упростите выражение:

IV. Новая тема. Решение линейных уравнений.

До сегодняшнего урока мы не умели решать уравнения, в которых неизвестное находилось слева и справа от знака равенства: 3x+7=x+15. Некоторые из нас постоянно забывают правила нахождения неизвестного слагаемого, уменьшаемого, вычитаемого. Сегодня мы постараемся разрешить все эти затруднения.

Уравнение, которое можно привести к виду ax=b, где a и b − некоторые числа (a0), называется линейным уравнением с одним неизвестным.

Линейные уравнения обладают свойствами:

1. Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (стр. 229 учебника).
2. Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак (стр. 230 учебника).

Рассмотрим план решения линейного уравнения:

Какими из свойств равенств мы воспользовались для решения уравнения? (вторым)

Рассмотрим примеры уравнений, при решении которых будет удобно воспользоваться и первым свойством.

х+3=х+5 │∙9 Удобно умножить на наименьшее общее кратное знаменателей дробей.

(х+3)∙9=(х+5)∙9 Далее − по плану.

Видео:Раскрытие скобок. 6 класс.Скачать

Раскрытие скобок

Продолжаем изучать основы алгебры. В данном уроке мы научимся раскрывать скобки в выражениях. Раскрыть скобки означает избавить выражение от этих скобок.

Чтобы раскрывать скобки, нужно выучить наизусть два правила. При регулярных занятиях раскрывать скобки можно с закрытыми глазами, и про те правила которые требовалось заучивать наизусть, можно благополучно забыть.

Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Первое правило раскрытия скобок

Рассмотрим следующее выражение:

Значение данного выражения равно 2. Раскроем скобки в данном выражении. Раскрыть скобки означает избавиться от них, не влияя на значение выражения. То есть после избавления от скобок значение выражения 8 + (−9 + 3) по прежнему должно быть равно двум.

Первое правило раскрытия скобок выглядит следующим образом:

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Итак, мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Этот плюс нужно опустить вместе со скобками. Иными словами, скобки исчезнут вместе с плюсом, который перед ними стоял. А то, что было в скобках запишется без изменений:

Мы получили выражение без скобок 8−9+3 . Данное выражение равно 2, как и предыдущее выражение со скобками было равно 2.

Таким образом, между выражениями 8+(−9+3) и 8−9+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

8 + (−9 + 3) = 8 − 9 + 3

Пример 2. Раскрыть скобки в выражении 3 + (−1 − 4)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:

3 + (−1 − 4) = 3 − 1 − 4

Пример 3. Раскрыть скобки в выражении 2 + (−1)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:

В данном примере раскрытие скобок стало своего рода обратной операцией замене вычитания сложением. Как это понимать?

В выражении 2 − 1 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 2 + (−1) . Но если в выражении 2 + (−1) раскрыть скобки, то получится изначальное 2 − 1 .

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после каких-нибудь преобразований. То есть избавить его от скобок и сделать проще.

Чтобы упростить данное выражение, можно привести подобные слагаемые. Напомним, что для приведения подобных слагаемых, нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

Получили выражение 3a + (−4b) . В этом выражении раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок, то есть опускаем скобки вместе с плюсом, который стоит перед этими скобками:

Таким образом, выражение 2a+a−5b+b упрощается до 3a−4b .

Раскрыв одни скобки, по пути могут встретиться другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в следующем выражении:

Здесь два места, где нужно раскрыть скобки. В данном случае применимо первое правило раскрытия скобок, а именно опускание скобок вместе с плюсом, который стоит перед этими скобками:

2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6

Пример 3. Раскрыть скобки в выражении 6+(−3)+(−2)

В обоих местах, где имеются скобки, перед ними стоит плюс. Здесь опять же применяется первое правило раскрытия скобок:

6 + (−3) + (−2) = 6 − 3 − 2

Иногда первое слагаемое в скобках записано без знака. Например, в выражении 1+(2+3−4) первое слагаемое в скобках 2 записано без знака. Возникает вопрос, а какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ напрашивается сам — перед двойкой будет стоять плюс.

На самом деле даже будучи в скобках перед двойкой стоит плюс, но мы его не видим по причине того, что его не записывают. Мы уже говорили, что полная запись положительных чисел выглядит как +1, +2, +3 . Но плюсы по традиции не записывают, поэтому мы и видим привычные для нас положительные числа 1, 2, 3 .

Поэтому, чтобы раскрыть скобки в выражении 1+(2+3−4) , нужно как обычно опустить скобки вместе с плюсом, стоящим перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

1 + (2 + 3 − 4) = 1 + 2 + 3 − 4

Пример 4. Раскрыть скобки в выражении −5 + (2 − 3)

Перед скобками стоит плюс, поэтому применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед этими скобками. Но первое слагаемое, которое в скобках записываем со знаком плюс:

−5 + (2 − 3) = −5 + 2 − 3

Пример 5. Раскрыть скобки в выражении (−5)

Перед скобками стоит плюс, но он не записан по причине того, что до него не было других чисел или выражений. Наша задача убрать скобки, применив первое правило раскрытия скобок, а именно опустить скобки вместе с этим плюсом (даже если он невидим)

Пример 6. Раскрыть скобки в выражении 2a + (−6a + b)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:

Пример 7. Раскрыть скобки в выражении 5a + (−7b + 6c) + 3a + (−2d)

В данном выражении имеется два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:

Видео:РАСКРЫТИЕ СКОБОК В УРАВНЕНИИ. Примеры | МАТЕМАТИКА 6 классСкачать

Второе правило раскрытия скобок

Теперь рассмотрим второе правило раскрытия скобок. Оно применяется тогда, когда перед скобками стоит минус.

Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный.

Например, раскроем скобки в следующем выражении

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, стоящим перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Мы получили выражение без скобок 5 + 2 + 3 . Данное выражение равно 10, как и предыдущее выражение со скобками было равно 10.

Таким образом, между выражениями 5−(−2−3) и 5+2+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

5 − (−2 − 3) = 5 + 2 + 3

Пример 2. Раскрыть скобки в выражении 6 − (−2 − 5)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок, а именно опускаем скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, записываем с противоположными знаками:

6 − (−2 − 5) = 6 + 2 + 5

Пример 3. Раскрыть скобки в выражении 2 − (7 + 3)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

2 − (7 + 3) = 2 − 7 − 3

Пример 4. Раскрыть скобки в выражении −(−3 + 4)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 5. Раскрыть скобки в выражении −(−8 − 2) + 16 + (−9 − 2)

Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить второе правило раскрытия скобок, а когда очередь доходит до выражения +(−9 − 2) нужно применить первое правило:

−(−8 − 2) + 16 + (−9 − 2) = 8 + 2 + 16 − 9 − 2

Пример 6. Раскрыть скобки в выражении −(−a − 1)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 7. Раскрыть скобки в выражении −(4a + 3)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 8. Раскрыть скобки в выражении a − (4b + 3) + 15

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 9. Раскрыть скобки в выражении 2a + (3b − b) − (3c + 5)

Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить первое правило раскрытия скобок, а когда очередь доходит до выражения −(3c+5) нужно применить второе правило:

2a + (3b − b) − (3c + 5) = 2a + 3b − b − 3c − 5

Пример 10. Раскрыть скобки в выражении −a − (−4a) + (−6b) − (−8c + 15)

Здесь три места, где нужно раскрыть скобки. Вначале нужно применить второе правило раскрытия скобок, затем первое, а затем опять второе:

−a − (−4a) + (−6b) − (−8c + 15) = −a + 4a − 6b + 8c − 15

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Механизм раскрытия скобок

Правила раскрытия скобок, которые мы сейчас рассмотрели, основаны на распределительном законе умножения:

На самом деле раскрытием скобок называют ту процедуру, когда общий множитель умножают на каждое слагаемое в скобках. В результате такого умножения скобки исчезают. Например, раскроем скобки в выражении 3×(4+5)

3 × (4 + 5) = 3 × 4 + 3 × 5

Поэтому, если нужно умножить число на выражение в скобках (или выражение в скобках умножить на число) надо говорить раскроем скобки.

Но как связан распределительный закон умножения с правилами раскрытия скобок, которые мы рассматривали ранее?

Дело в том, что перед любыми скобками стоит общий множитель. В примере 3 × (4 + 5) общий множитель это 3 . А в примере a(b + c) общий множитель это переменная a .

Если перед скобками нет чисел или переменных, то общим множителем является 1 или −1 , в зависимости от того, какой знак стоит перед скобками. Если перед скобками стоит плюс, значит общим множителем является 1 . Если перед скобками стоит минус, значит общим множителем является −1 .

К примеру, раскроем скобки в выражении −(3b − 1) . Перед скобками стоит минус, поэтому нужно воспользоваться вторым правилом раскрытия скобок, то есть опустить скобки вместе с минусом, стоящим перед скобками. А выражение, которое было в скобках, записать с противоположными знаками:

Мы раскрыли скобки, воспользовавшись правилом раскрытия скобок. Но эти же скобки можно раскрыть, воспользовавшись распределительным законом умножения. Для этого сначала записываем перед скобками общий множитель 1, который не был записан:

Минус, который раньше стоял перед скобками относился к этой единице. Теперь можно раскрыть скобки, применяя распределительный закон умножения. Для этого общий множитель −1 нужно умножить на каждое слагаемое в скобках и полученные результаты сложить.

Для удобства заменим разность, находящуюся в скобках на сумму:

Далее умножаем общий множитель −1 на каждое слагаемое в скобках:

Как и в прошлый раз мы получили выражение −3b + 1 . Каждый согласится с тем, что в этот раз затрачено больше времени на решение столь простейшего примера. Поэтому разумнее пользоваться готовыми правилами раскрытия скобок, которые мы рассматривали в данном уроке:

Но не мешает знать, как эти правила работают.

В данном уроке мы научились ещё одному тождественному преобразованию. Вместе с раскрытием скобок, вынесением общего за скобки и приведением подобных слагаемых можно немного расширить круг решаемых задач. Например:

Раскрыть скобки и привести подобные слагаемые в следующем выражении:

Здесь нужно выполнить два действия — сначала раскрыть скобки, а потом привести подобные слагаемые. Итак, по порядку:

1) Раскрываем скобки:

2) Приводим подобные слагаемые:

В получившемся выражении −10b+(−1) можно раскрыть скобки:

Пример 2. Раскрыть скобки и привести подобные слагаемые в следующем выражении:

1) Раскроем скобки:

2) Приведем подобные слагаемые. В этот раз для экономии времени и места, не будем записывать, как коэффициенты умножаются на общую буквенную часть

Пример 3. Упростить выражение 8m+3m и найти его значение при m=−4

1) Сначала упростим выражение. Чтобы упростить выражение 8m+3m , можно вынести в нём общий множитель m за скобки:

2) Находим значение выражения m(8 + 3) при m = −4 . Для этого в выражение m(8 + 3) вместо переменной m подставляем число −4

m (8 + 3) = −4 (8 + 3) = −4 × 8 + (−4) × 3 = −32 + (−12) = −44

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Тренажер по теме «Раскрытие скобок и упрощение выражений» (6 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выберите документ из архива для просмотра:

Выбранный для просмотра документ 6кл тренажер раскрытие скобок (задания).doc

№ 1 Раскройте скобки

№ 2 Раскройте скобки и найдите значение выражений:

10. -2,78 + (7,78 — 1,3)

11. (2 — 1,51) — (3,13 — 0,51) + (0,13 — 0,5)

12. -(0,39 + 2,1) + (0,13 • 3 — 2,1) — 0,8

13. (4,3918 — 16,4) — (4,3917 — 4,1 • 4)

14. (3,29 + 1) — (1,2 + 1) — (1 — 0,91)

№ 3 Раскройте скобки и упростите выражение

№ 4 Раскройте скобки и упростите выражение

2. — (a — x — 3) — (x — a + 2)

3. (a + 3,3 — a) — (3,3 + x)

7. — (m — 3,8) + (4,12 + m)

8. — (2,43 + x — b) — (2,43 + b — x)

9. — (1,53 — x + 1) — (x — a — 2,53)

10. — (a — x) — (5,1 + x) + a — 5,1

11. (b — x) — (a — x) + (a — b)

12. — (a + 3,3) — (x — a) — 3,3 + x

13. (2,43 + 1,1) — (b + 2,43) + (b — 1,1)

14. (1,53 — x + a) — (x — 1,53 — a) — a

15. — (a — 1,21) — (1 — a) — (0,21 — a)

3 Раскройте скобки и упростите выражение

№ 4 Раскройте скобки и упростите выражение

2. — (a — x — 3) — (x — a + 2)

3. (a + 3,3 — a) — (3,3 + x)

7. — (m — 3,8) + (4,12 + m)

8. — (2,43 + x — b) — (2,43 + b — x)

9. — (1,53 — x + 1) — (x — a — 2,53)

10. — (a — x) — (5,1 + x) + a — 5,1

11. (b — x) — (a — x) + (a — b)

12. — (a + 3,3) — (x — a) — 3,3 + x

13. (2,43 + 1,1) — (b + 2,43) + (b — 1,1)

14. (1,53 — x + a) — (x — 1,53 — a) — a

15. — (a — 1,21) — (1 — a) — (0,21 — a)

Выбранный для просмотра документ 6кл тренажер раскрытие скобок (ответы).docx

№ 1 Раскройте скобки

— 4a + 16c – 24d + 4n

№ 2 Раскройте скобки и найдите значение выражений:

№ 3 Раскройте скобки и упростите выражение

№ 4 Раскройте скобки и упростите выражение

№ 1 Раскройте скобки

— 4a + 16c – 24d + 4n

№ 2 Раскройте скобки и найдите значение выражений:

№ 3 Раскройте скобки и упростите выражение

№ 4 Раскройте скобки и упростите выражение

№ 3 Раскройте скобки и упростите выражение

№ 4 Раскройте скобки и упростите выражение

Краткое описание документа:

Данный тренажер по теме «Раскрытие скобок и упрощение выражений» помогает усовершенствовать навыки и умения детей по данной теме. Тренажер состоит из 35 заданий, разбитых на группы:

1) Раскройте скобки

2) Раскройте скобки и найдите значение выражений

3) Раскройте скобки и упростите выражение (простые задания)

4) Раскройте скобки и упростите выражение (повышенного уровня задания)

Данная разработка была использована частично на уроке на этапе обобщения и систематизации знаний по данной теме, частично в виде индивидуального домашнего задания и частично на уроке закрепления изученного материала в групповой работе.

К тренажеру прикреплены ответы, которые помогут учителю облегчить на уроке этап самопроверка или взаимопроверки учеников.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 930 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 687 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 304 человека из 68 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Решение уравнений, 6 классСкачать

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 594 725 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 07.01.2017
• 2295
• 39

• 07.01.2017
• 483
• 0

• 07.01.2017
• 413
• 0

• 07.01.2017
• 641
• 3

• 07.01.2017
• 4505
• 395

• 07.01.2017
• 931
• 5

• 07.01.2017
• 357
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 07.01.2017 46264
• ZIP 127.2 кбайт
• 1789 скачиваний
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Подоляк Оксана Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 1 месяц
• Подписчики: 0
• Всего просмотров: 74675
• Всего материалов: 15

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Как решать уравнения со скобками быстро и правильно. Математика 6 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Время чтения: 1 минута

В приграничных пунктах Брянской области на день приостановили занятия в школах

Время чтения: 0 минут

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Время чтения: 0 минут

Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи

Время чтения: 1 минута

Минпросвещения России подготовит учителей для обучения детей из Донбасса

Время чтения: 1 минута

РДШ организовало сбор гуманитарной помощи для детей из ДНР

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🌟 Видео

Подобные слагаемые. Приведение подобных слагаемых. 6 класс.Скачать

6 класс, 39 урок, Раскрытие скобокСкачать

Математика 6 класс (Урок№30 - Раскрытие скобок и заключение в скобки.)Скачать

Математика 6 класс. РАСКРЫТИЕ СКОБОК. РЕШЕНИЕ УРАВНЕНИЙ.Скачать

Как решать уравнения со скобками.Как правильно раскрывать скобки.Скачать

Ставим правильно знаки при раскрытии скобок.Скачать

Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Раскрытие скобок и приведение подобных слагаемых. 6 класс.Скачать

Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравненияСкачать

Уравнение с раскрытием скобок. #математика #алгебра #уравнение #скобки #минус #simplemathСкачать

Решение уравнений - математика 6 классСкачать