Уравнения с параметром 7 класс алгебра (5 видео)

«Линейные уравнения с параметрами». 7-й класс

Класс: 7

Содержание

Презентация к уроку
Решение уравнений с параметрами 7 класс
Просмотр содержимого документа «Решение уравнений с параметрами 7 класс»
План- конспект урока «Решение линейных уравнений с параметрами», 7 класс учебно-методический материал по алгебре (7 класс) на тему
Скачать:
Предварительный просмотр:
🔥 Видео

Презентация к уроку

Загрузить презентацию (327 кБ)

Цели урока:

Обучающая: формировать умение решать линейные уравнения с параметрами.
Развивающая:
- развивать исследовательскую деятельность учащихся;
- развивать логическое мышление для сознательного восприятия учебного материала;
- развивать внимание, зрительскую память, активность учащихся на уроке.

Тип урока: введение нового материала.

Учебник: «Алгебра-7» авт. Ю.Н.Макарычев, Н.Г. Миндюк и др. издательство «Мнемозина», 2008 год.

I. Проверка домашнего задания (работа выполнялась на двойных листах и сдаётся на проверку).

Готовые решения проецируются на доску и разбирается (проговаривается) алгоритм решения.

№ 624. Решите уравнение:

а) 0,3(2x – 1) – 0,4 (x + 8) = 1,2x – 1;
0,6x – 0,3 – 0,4x – 3,2 = 1,2x – 1;
0,6x – 0,4x –1,2x = 0,3 + 3,2– 1;
– x = 2,5;
x = –2,5. Ответ: – 2,5.

в) – 6(2 – 0,2x) + 11 = – 4(3 – 0,3x) – 1;
– 12 + 1,2x + 11 = – 12 + 1,2x – 1;
1,2x – 1,2x = 12 – 11 + 1;
0x = 2. Ответ: решений нет.

№ 625. Решите уравнение

а) (2x – 1)(3x + 7) – (1 + 6x)(x + 2) = 4;
6x 2 + 14x – 3x – 7 – (x + 2 + 6×2 + 12x) = 4;
6x 2 + 14x – 3x – 7 – x – 2 – 6×2 – 12x = 4;
6x 2 + 14x – 3x – x – 6x 2 – 12x = 4 + 7 + 2;
– 2x = 13;
x = – 6,5. Ответ: – 6,5.

№ 626. Решите уравнение

№ 622. При каких значениях a уравнение ax = 2a – 1:

а) имеет единственный корень; (при a 0)
б) имеет бесконечно много корней; (таких значений a нет)
в) не имеет корней? (при a = 0).

II. Устная работа (задания проецируются на доску)

1. Найдите корни уравнения:

а) 14 + 3x = 5 – x ; (– 2,25)
б) 105y – 28 = 105y + 7;
в) 34x + 2 = 34x + 2. (x – любое число)

2. При каких значениях a число 3 является корнем уравнения?

а) ax = – 6; (при a = – 2)
б) 8x = 3a . (при a = 8)

3. Укажите контрольные значения, при которых уравнение не имеет решений или решением является любое число?

а) (5 – a) x = 0; б) (b + 4) x = 5; в) ax = x.

III. Изучение нового материала

Учитель. Сегодня на уроке мы с вами будем учиться решать линейные уравнения с параметрами.

Задание 1

Рассмотрим уравнение mx + 3 = 4m – 2x. Оно содержит две переменные: m и x.

1. Вопрос. Чем же они отличаются? (одна из переменных, например m, принимает любые значения, тогда переменная x принимает не все значения, а только те, которые получаются при заданных значениях переменной m).

2. Задание. Решите данное уравнение при m = 2, – 1, 0.

если m = 2, то уравнение примет вид 2x + 3 = 8 – 2x. Ответ: ;
если m = – 1, то уравнение примет вид – x + 3 = – 4 – 2x. Ответ: – 7;
если m = 0, то уравнение примет вид 3 = – 2x. Ответ: – 1,5 )

3. Задание. Решите данное уравнение, задав свое значение для переменной m.
Переменную m, значения которой мы задаём, называют параметром (фиксированным числом).
Определение: решить уравнение с параметром – значит, для любых допустимых значений параметра найти значения неизвестной переменной.

4. Вопрос. Можем ли мы перебрать все значения параметра m, чтобы найти значения x? (нет)

5. Возникла проблемная ситуация. Как же решить данное уравнение mx + 3 = 4m – 2x?
Нет ли другого подхода к решению уравнения?
Оказывается существует. Для решения линейного уравнения с параметром применяется тот же
алгоритм решения, как и для линейного уравнения без параметра, т.е.перенос слагаемых и
приведение подобных слагаемых. Всегда ли эти операции выполняются? (да).
Выполним указанные операции:

6. Вопрос. Всегда ли можно выполнить деление? (нет).

7. Задание. Найдите контрольные значения, при которых уравнение не имеет решений.

Запишем решение уравнения далее так:

Задание 2 (разобрать так же подробно на доске)

Решите уравнение n 2 x + 3nx = 5n + 15;

n 2 x + 3nx = 5n + 15;
n (n + 3) x = 5 (n + 3);
n = – 3; 0 – контрольные значения параметра

1) при n = – 3 уравнение примет вид 0x = 0, x – любое число;
2) при n = 0 уравнение примет вид 0x = 15, решений нет;

Задание 3.

Самостоятельное решение уравнений с последующей проверкой на доске.

1. 2кx – 5(2 + x) = 7.

2кx – 5(2 + x) = 7;
2кx – 5x – 10 = 7;
2кx –5x = 7 + 10;
(2к –5) x = 17;
2к –5 = 0, к = 2,5 – контрольное значение параметра

1) при к = 2,5 уравнение примет вид 0x = 17, решений нет;

2. a 2 x – 2a = a 2 + ax

a 2 x – 2a = a 2 + ax;
a 2 x – ax = a 2 + 2a;
a(a – 1)x = a (a + 2);
a(a – 1) = 0, a = 0; 1 – контрольные значения параметра

1) при a = 0 уравнение примет вид 0x = 0, x – любое число;
2) при a = 1 уравнение примет вид 0x = 3, решений нет;

IV. Подведение итогов

1. Что мы сегодня рассматривали на уроке? (решение линейных уравнений с параметрами.)
2. В чем заключался алгоритм решения таких уравнений? Какие равносильные преобразования применяли?

а) освобождение от знаменателя, умножив обе части равенства на одно и тоже отличное от нуля число;
б) раскрытие скобок;
в) перенос слагаемых из одной части равенства в другую с противоположным знаком;
г) приведение подобных слагаемых.

V. Выставление оценок

VI. Домашнее задание

1) № 631; № 632; № 633.
2) Дополнительное задание

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Решение уравнений с параметрами 7 класс

в данной публикации содержатся примеры решения линейных уравнений с параметрами для учащихся 7 класса.

Просмотр содержимого документа
«Решение уравнений с параметрами 7 класс»

Примеры решения линейных уравнений, содержащие параметры.

Линейные уравнения с одним неизвестным могут содержать и другие буквы. Такие уравнения называют уравнениями с параметрами. Уравнения, содержащие параметры, решаются также, как и обычные линейные уравнения, но корни уравнения зависят от значений параметров и выражаются через них.

Пример 1. Решим уравнение относительно переменной x:

Перенесем члены уравнения, содержащие x, в левую часть, а все остальные – в правую часть уравнения:

Вынесем x в левой части за скобки:

При p = 5 получаем 0  x = 22, т.е. уравнение корней не имеет.

Если же p ≠ 5, то разделим обе части уравнения на 5 – p.

x = 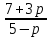– уравнение имеет единственный корень.

Ответ: при р ≠ 5 x = 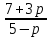; при р = 5 корней нет.

Мы нашли зависимость решения уравнения от параметра. Если решаем уравнения, содержащие параметры, мы можем сказать, при каких значениях параметра уравнение имеет единственное решение, когда решений бесконечное множество, а в каких случаях их нет вообще.

Пример 2. Решим уравнение относительно переменной x:

Умножим обе части уравнения для удобства на -1:

x =

Это выражение имеет смысл при любых значениях c и b поэтому уравнение имеет единственное решение.

Ответ: x =

Пример 3. Решим уравнение относительно переменной y:

Если b = 3 и 2 – 2a ≠ 0 (a ≠ 1), то корней нет, т.к. получим равенство, которое не выполняется ни при каких значениях переменной.

Если b = 3 и a = 1, то получим 0  y = 0. Уравнение имеет бесконечное множество решений.

Если b ≠ 3, то y = 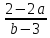– единственный корень.

Ответ: при b ≠ 3 y = 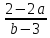; при b = 3 и a = 1 – бесконечно много решений; при b = 3 и a ≠ 1 – корней нет.

Видео:Уравнения с параметром. Алгебра 7 класс.Скачать

План- конспект урока «Решение линейных уравнений с параметрами», 7 класс
учебно-методический материал по алгебре (7 класс) на тему

Представлен конспект урока алгебры в 7 классе по теме «Решение линейных уравнений с параметрами». Это урок обобщения и систематизации знаний и умений. В конце приводится самоанализ проведенного урока.

Видео:Уравнения с параметром. Алгебра, 8 классСкачать

Скачать:

Вложение	Размер
plan-konspekt_uroka_7_klass_parametry.doc	110 КБ

Видео:Линейные уравнения с параметром 7-8 ые классыСкачать

Предварительный просмотр:

Конспект открытого урока в 7 классе по теме «Решение линейных уравнений с параметрами»

Цель урока: обобщить и систематизировать знания по теме «Линейные уравнения с параметром», способствовать формированию навыков решения линейных уравнений с параметром, знакомство учащихся с новыми понятиями, расширение их математического образования.

Образовательная – показать алгоритм решения уравнений, формировать осознанный подход к решению уравнений с параметром;
Развивающая – способствовать развитию логического мышления, навыков исследовательской деятельности, творческих способностей, интуиции.
Воспитательная – воспитать самостоятельность, ответственность, способствовать формированию алгоритмической культуры, рациональному использованию времени.

Тип урока : урок повторения, обобщения и систематизации знаний.

Оборудование : компьютер, проектор

Форма организации учебной деятельности:

1) усовершенствованная математическая речь учеников;

2) ученики приобретают знания о методе решения линейных уравнений с параметром и совершенствуют его применение.

I. Организационный момент

Сформулировать тему урока и его цели

II. Актуализация знаний учащихся

Вспомним решение простейшего линейного уравнения ax = b.

Показать на экране:

Найдите корни уравнения

а) 3 + х = 4 – х, (0,5)

б) 9х — 4 = 9х + 5, ( ø )

в) 3х + 1 = 3х + 1. (х принадлежит R)

При каких значениях b число 3 является корнем уравнения?

4. Решить уравнение:

Данное уравнение содержит параметр.

На экране показать:

Параметр – неизвестная величина, которая считается постоянной при решении конкретной задачи.

Решить уравнение с параметром – значит найти все решения этого уравнения для каждого допустимого значения параметра.

В правой части уравнения конкретное число, не равное нулю, следовательно, решение данного уравнения будет зависеть от значения параметра а :

Если а = 0, то уравнение имеет вид 0 • х = 8, такое уравнение решений не имеет.

Если а ≠ 0, то х = а / 8.

Если а = 0, то уравнение примет вид 0х = 0, а решением данного уравнения является х – любое число; если а ≠ 0, то х = 1

Решите уравнение с параметром:

а) , (если m = 0 то x принадлежит R; если m ≠ 0, то решений нет)

в) (если а = 0, то решений нет; если а не равен 0, то х = а /4).

Назовите одно из решений уравнения .

III. Решение уравнений:

а) (а — 2)х = 10 – 5х (решает учитель)

Приведем данное уравнение к виду ах = в:

Выясним при каком значении параметра а коэффициент перед х обратится в ноль:

3 + а = 0 а = -3 (назовем его контрольным значением параметра)

1) если а = -3, то 0 • х = 10, а значит корней нет;

2) если а ≠ -3, то х = 10/ (3 + а)

Ответ: при а = -3 корней нет, при а ≠ -3 х = 10/(3 +а)

б) (n 2 – 9)x + 4 = 2(x + 6) – 7x (решают учащиеся)

n 2 x – 9x + 4 = 2x + 12 -7x

n 2 x – 9x -2x + 7x = 12 – 4

Найдем контрольные значения параметра

n 2 – 4 = 0; n 2 = 4; n = 2 или n = -2

n = ± 2, то уравнение примет вид 0 • х = 8, значит корней нет;
n ≠ ± 2, то х = 8/( n 2 – 4)

Ответ: при n = ± 2 корней нет, при n ≠ ± 2 х = 8/( n 2 – 4)

в) а 3 х + 6 = а 2 + 4ах – а

а(а 2 – 4)х = а 2 – а – 6

Контрольные значения параметра:

а = 0 или (а 2 – 4) = 0

1) при а = 0 уравнение примет вид 0 • х = -6, значит корней нет;

2) при а = 2 получим 0 • х = -4 , значит корней нет;

3) при а = -2 получим 0 • х = 0 , то х – любое число;

4) если а ≠ ±2 и а ≠ 0, то х = ( а 2 – а – 6)/(а(а 2 – 4)).

Ответ: при а = 0 или а = 2 решений нет;

при а = -2 х – любое число;

если а ≠ ±2 и а ≠ 0, то х = ( а 2 – а – 6)/(а(а 2 – 4)).

Текст самостоятельной работы показать на экране:

а 2 х – а 2 = х – а;

2х + 3а = 10 + 5а + ах

Самопроверка.

На экране высвечивается решение уравнений.

а 2 х – а 2 = х – а;

а 2 х – х = а 2 – а

х(а 2 – 1) = а 2 – а

Контрольные значения параметра:

а = 1, то уравнение примет вид: 0 • х = 0, значит х – любое число;
а = -1, то получим уравнение 0 • х = 2, тогда корней нет;
а ≠ ±1, тогда х = (а 2 – а)/ (а 2 – 1)

х = а(а — 1)/((а – 1)(а + 1

Ответ: при а = 1 х – любое число;

При а = -1 тогда корней нет;

При а ≠ ±1 х = а/(а +1)

2х + 3а = 10 + 5а + ах

2х – ах = 10 + 5а – 3а

Контрольные значения параметра

если а = 2, то уравнение примет вид 0 • х = 10, значит корней нет;

если а ≠ 2, то х = (2а + 10)/(2 – а)

Ответ: 1) при а = 2 корней нет;

2) при а ≠ 2 х = (2а + 10)/(2 – а)

Задание с введением дополнительного условия

При каких значениях параметра а среди корней уравнения

2 ах – 4 х – а 2 + 4 а — 4 = 0 есть корни больше 1.

Решение: 2 ах – 4 х – а 2 + 4 а — 4 = 0

2( а -2) х = а 2 –4 а +4

2( а -2) х = ( а -2) 2

При а = 2, 0 х = 0 решением будет любое число, в том числе и большее 1.

При а ≠ 2 х = , по условию х > 1, то > 1, а >4 .

Ответ : при а ∈ ∪ (4 ; + ∞ ) .

1. Решите уравнение mx + 2 = — 1 относительно х .

А. x = — , при m ≠ 0

Б. 1) при m = 0 корней нет;

В. 1) при m = 0 корней нет

2. Решите уравнение k( х – 4 ) + 2( х + 1) = 1 относительно х .

А.1) при k = -2 корней нет;

Б.1) при k = — 2 корней нет

В.1) при k = 0 корней нет.

3) при k ≠ -2 , k ≠ х =

3. Решите уравнение 2 а ( а -2) х = а 2 -5 а +6 относительно х .

А. 1) при а =2 х ∈ R

2) при а =0 корней нет

3) при а ≠ 0 и а ≠ -2, х =

Б. 1) при а =2 х ∈ R

2) при а =0 корней нет

3) при а ≠ 0 и а ≠ 2, х =

В. 1) при а =2 х ∈ R

2) при а =0 корней нет

4) при а ≠ 2, а ≠ 0, а ≠ 3 х =

4. При каких значениях b уравнение 1+2 х – bх =4+ х имеет отрицательное решение?

А.При b b > 1 В. При b

1. Решите уравнение (m – 2) х = 3 относительно х .

А. x = — , при m ≠ 0

Б. 1) при m = 2 корней нет;

В. 1) при m = 2 корней нет

2. Решите уравнение а (3 х -2) =6 х – 4 относительно х .

А.1) при а = 2 x – любое число;

Б.1) при а = -2 корней нет

В.1) при а = 0 корней нет.

3) при а ≠ -2 , а ≠ х =

3. Решите уравнение 3 ах – 6 х – а 2 + 4 а — 4 = 0 относительно х .

А. 1) при а =2 х ∈ R

2) при а =0 корней нет

3) при а ≠ 0 и а ≠ -2, х =

Б. 1) при а =2 х ∈ R

В. 1) при а =2 х ∈ R

2) при а =0 корней нет

4) при а ≠ 2, а ≠ 0, а ≠ 3 х =

4. При каких значениях b среди корней уравнения х – b х + b 2 – 1=0 есть корни больше 1?

А.При b > -1 Б. При b > 0 В. При b

Код верного ответа

а) (2 b – 3 x ) + ( x – 5 b ) = 4 x + 6 b

б) (2 x – c ) – (5 c – x ) = 3 c

При каких значениях параметра с корень уравнения х+с=3х-5 является неотрицательным числом?
При каких значениях параметра а корень уравнения 4а+12х=4ах-3а+6 больше 3?

1. В классе обучаются 29 учащихся. 10 учащихся могут учиться на 4-5, 13 человек на четвёрки, остальные без направляющей помощи учиться не могут. При планировании урока это было учтено и определило выбор методов и приёмов изложения материала и способов закрепления полученных знаний на основе систематизации .

2. Этот урок является уроком обобщения и систематизации знаний и умений. Материал урока направлен на развитие логического мышления, алгоритмической культуры, интуиции, навыков исследовательской деятельности, творческих способностей учащихся. Задачи подобраны одно-двухшаговые и алгоритмичные по своему решению. Структура урока: постановка цели и задач урока; повторение умений и навыков, являющихся опорой для обобщения и систематизации знаний по данной теме; проведение проверочных упражнений (устное решение уравнений); ознакомление с алгоритмом решения линейных уравнений с параметром, упражнения на закрепление данного алгоритма; тренировочные упражнение по образу и подобию в виде самостоятельной работы; самоконтроль учащихся; решение уравнений с дополнительным условием, предполагающие элементы творчества в деятельности учащихся

3. На уроке решались следующие задачи:

Обобщить и систематизировать знания по теме «Линейные уравнения с параметром», Изучить алгоритм решения линейных уравнений с параметром, формировать у учащихся осознанный подход к решению уравнений с параметром. Способствовать развитию логического мышления. Воспитание самостоятельности, ответственности, способствовать формированию алгоритмической культуры, рациональному использованию времени.

Комплексность их решения продумана. Главными были обучающие задачи, при их решении попутно решались и развивающие, и воспитывающие задачи. Развивающая задача решалась через приёмы доступного изучения материала, а воспитывающая уже на этапе выбора класса для открытого урока, во время самопроверки.

4. Данная структура урока продиктована тем, что класс сильный, большинство учащихся активно работают на уроке, способны быстро воспринимать информацию. Поэтому урок плотнен и динамичен на всех этапах. Опрос проводился с целью актуализации имеющихся знаний. Связки между этапами логичны. Домашнее задание содержит четыре номера.

5. Главный акцент делался на понятиях: линейное уравнение, параметр, контрольные значения параметра, алгоритм решения линейного уравнения с параметром. Выбраны задания различного вида: линейные уравнения стандартного вида, уравнения, которые нужно привести к стандартному виду, линейные уравнения с дополнительным условием. Существенным этапом решения задач с параметрами является запись ответа.

6. Методы обучения выбраны частично-поисковые, наглядные, деятельностные.

7. Необходимости применения методов дифференцированного обучения не было. Достаточно оказания индивидуальной помощи.

8. Контроль усвоения знаний осуществлялся наблюдением за самостоятельностью и активностью учащихся на первых этапах урока, в конце урока была дана самостоятельная работа в форме теста.