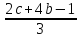Уравнения с параметрами и методы их решения 7 класс алгебра

в данной публикации содержатся примеры решения линейных уравнений с параметрами для учащихся 7 класса.

Просмотр содержимого документа
«Решение уравнений с параметрами 7 класс»

Примеры решения линейных уравнений, содержащие параметры.

Линейные уравнения с одним неизвестным могут содержать и другие буквы. Такие уравнения называют уравнениями с параметрами. Уравнения, содержащие параметры, решаются также, как и обычные линейные уравнения, но корни уравнения зависят от значений параметров и выражаются через них.

Пример 1. Решим уравнение относительно переменной x:

Перенесем члены уравнения, содержащие x, в левую часть, а все остальные – в правую часть уравнения:

Вынесем x в левой части за скобки:

При p = 5 получаем 0  x = 22, т.е. уравнение корней не имеет.

Если же p ≠ 5, то разделим обе части уравнения на 5 – p.

x = 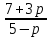– уравнение имеет единственный корень.

Ответ: при р ≠ 5 x = 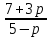; при р = 5 корней нет.

Мы нашли зависимость решения уравнения от параметра. Если решаем уравнения, содержащие параметры, мы можем сказать, при каких значениях параметра уравнение имеет единственное решение, когда решений бесконечное множество, а в каких случаях их нет вообще.

Пример 2. Решим уравнение относительно переменной x:

Умножим обе части уравнения для удобства на -1:

x =

Это выражение имеет смысл при любых значениях c и b поэтому уравнение имеет единственное решение.

Ответ: x =

Пример 3. Решим уравнение относительно переменной y:

Если b = 3 и 2 – 2a ≠ 0 (a ≠ 1), то корней нет, т.к. получим равенство, которое не выполняется ни при каких значениях переменной.

Если b = 3 и a = 1, то получим 0  y = 0. Уравнение имеет бесконечное множество решений.

Если b ≠ 3, то y = 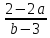– единственный корень.

Ответ: при b ≠ 3 y = 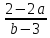; при b = 3 и a = 1 – бесконечно много решений; при b = 3 и a ≠ 1 – корней нет.

Видео:Уравнения с параметром. Алгебра 7 класс.Скачать

Линейные уравнения с параметрами в 7-м классе (методические рекомендации)

Разделы: Математика

Известно, что в программе по математике для неспециализированных школ задачам с параметрами отводится незначительное место.
К задачам с параметрами, рассматриваемым в школьном курсе, относятся, например, задачи, в которых отыскивается решение линейных и квадратных уравнений в общем виде, исследуется количество их корней в зависимости от значений параметров.
Естественно, что такой небольшой класс задач не позволяет учащимся овладеть методами решения задач с параметрами. В результате, у учащихся возникает психологический барьер уже при «первом» знакомстве с параметрами — это неизвестное и известное, переменная и постоянная. Выход из сложившейся ситуации — включать задачи с параметрами в каждую тему.

• Для решения задач с параметрами требуется:

а) свободное владение навыками решения уравнений;
б) знание специфических преобразований, которые используются в уравнениях;
в) умение построить логическую цепочку рассуждений.

а) отработку навыков решения уравнений;
б) повышают интеллектуальный уровень ученика и его логическое мышление;
в) формируют навыки исследовательской деятельности;
г) повышают интерес к математике.

Прежде чем ввести понятие «параметр», учащимся необходимо напомнить роль букв в алгебре. Обратить внимание ребят на то, что за буквой скрывается число.
Предложите учащимся задания, в которых надо выразить одну переменную через другую. К этим задачам надо возвращаться постоянно, особенно в 7-м классе, поскольку умение выражать одну переменную через другую очень пригодится при решении задач по физике, где требуется вначале составить буквенное выражение и только затем подставить числовые значения.

Пример №2.
Выразить х : а) ах = а-1; б) (а+2) х = а-1; в) а х = а -1.
Укажите, при каких значениях а имеет смысл полученное выражение.
Найдите значение х при а=2; а=3; а= -10.
Повторите на простых примерах, что такое уравнение, что значит решить уравнение. При решении уравнений типа 2х-2=-1;14х=-4; 3-3х=1 обратите внимание учащихся на то, что мы выразили неизвестное, которое надо найти, через числа.
Покажите, что в уравнение, помимо неизвестного, могут быть введены и другие буквы, и буквенные выражения. Например, ах=а-1, (а+2)х=а-1, (а+2)х=(а+2)-1, а х=а -1.
При этом, как всегда в алгебре, мы полагаем, что буквы могут принимать любые числовые значения. Например, задавая произвольно значения а для уравнения ах=а-1 получаем
при а=2 имеем 2х=2-1; при а=3 имеем 3х=3-1; при а=0 имеем 0х=0-1; при а=-4 имеем -4х=-4-1.

Пример №3.
Дано уравнение ах=5а-9.
Напишите уравнение, которое получится, если а=10; а=-2; а=0.

Пример №4.
Решить уравнение относительно х:
х+2=а+7.
Решение: х=а+5.
Переменную, которую надо найти, будем называть неизвестной, а переменную, через которую будем выражать искомую неизвестную, назовем параметром.

• Параметр — это переменная величина, которая в процессе решения уравнения (задачи) считают фиксированной и относительно которойпроводится анализ полученного решения.
• Решить уравнение с параметром — этозначит для каждого значения параметра найти значение неизвестной переменной, удовлетворяющее этому уравнению.

Заметим, что в нашем примере параметр а может принимать любые значения.
Ответ запишем так: при любом значении параметра а

х=а+5 .
Основное, что нужно усвоить при первом «знакомстве» с параметром, это необходимость осторожного обращения с фиксированным, но неизвестным числом. Необходимость аккуратного обращения с параметром хорошо видна в примерах, где замена параметра числом делает задачу банальной. К таким задачам, например, относятся задачи, в которых требуется сравнить два числа.

Пример №5.
Сравнить числа: а) а и 3а;
б) -а и 3а.
Решение:
а) естественно рассмотреть три случая:
если а 3а; если а = 0, то а = 3а; если а > 0, то а 3а; если а = 0, то -а = 3а; если а > 0, то -а -1 уравнение имеет два корня.

Как было сказано ранее, к уравнениям с параметрами надо возвращаться постоянно. Поэтому, на конец учебного года можно вынести уравнения:
1) (а-3)х=а2-9;
2) (3-2а)х=4а2-12а+9;
3) (а2-4)х=а2-5а+6;
4) (а2-1)х=а3+1
Решение.1) (а2-1)=0, а=±1.
При а=1 уравнение имеет вид 0х=2. Следовательно, решений нет.
При а=-1 уравнение имеет вид 0х=0. Следовательно, х- любое число.

Задачи для самостоятельного решения.

Для всех значений параметров а и в решите уравнения:

1. (5а+1)х+25а2+10а+1=0;
2. ах-а=х-1;
3. (а2-4)х=а2+а-2;
4. (а2-1)х-а2+2а-1=0;
5. (а-2в)х+а+в=3;
6. 
7. каких значениях параметра а уравнение а2(х-2)=х+а-3 имеет бесконечное множество решений?
8. каком значении параметра а корень уравнения х+3=2х-а будет отрицательным числом?
9. каждого значения параметра а определить число корней уравнения |x-1| =а.
10. каждого значения параметра а определить число корней уравнения|5x-3| =а.

Используемая литература.

1. Газета «Математика». Учебно-методическое приложение к газете «Первое сентября»: Е.Пронина, « Линейные уравнения с параметрами» №12, 2000 г.; C.Неделяева, «Особенности решения задач с параметрами» №34, 1999 г.
2. Азаров А.И., Барвенов С.А., Федосенко В.С. Методы решения задач с параметрами. Математика для старшеклассников. Минск: «Аверсэв», 2003.
3. Мочалов В.В., Сильвестров В.В. Уравнения и неравенства с параметрами. Чебоксары: Изд-во Чувашского университета, 2004.
4. Соколовская С.И., ДухонМ.Ю. Линейные уравнения и неравенства с параметром. Пособие для учащихся старших классов. М., 2005.

Видео:Решение уравнений, сводящихся к линейным | Алгебра 7 класс #18 | ИнфоурокСкачать

Урок по алгебре в 7,8 классе «Линейное уравнение с параметром и его решение в общем виде»
план-конспект урока по алгебре (8 класс) на тему

На уроке даётся определение линейного уравнения с параметром, рассматриваются способы его решения, Изучается схема исследования линейных уравнений с параметрами. Формируются навыки решения линейных уравнений с параметрами. Все рассмотренные задания в данной работе имеют цель – помочь учащимся составить представление о параметре, о том, что значит решить уравнение с ним. Выявить наиболее общие подходы к решению линейных уравнений с параметрами. Сформировать понимание основных методов решения линейных уравнений с параметрами.

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Скачать:

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Предварительный просмотр:

Рычкова Ирина Владимировна

МБОУ СОШ №23 г. Симферополь,

Республика Крым, Россия

Учитель высшей категории

Тема: Линейное уравнение с параметром и его решение в общем виде.

Образовательные: дать определение линейного уравнения с параметром, рассмотреть способы его решения, схему исследования линейных уравнений с параметрами. Формировать навыки решения линейных уравнений с параметрами.

Развивающие: развивать уровень математического и логического мышления, первоначальные навыки исследовательской деятельности.

Воспитательные: формирование волевые качества, формирование коммуникабельность, выработка объективной оценки своих достижений, формирование ответственности.

Поприветствовать учащихся, проверить их готовность к уроку, объявить тему урока и цель урока.

II. Проверка домашнего задания.

• ученики записывают на доске решения уравнений;
• обсуждение, замечания, уточнения к решениям на доске.

III. Актуализация опорных знаний учащихся.
№1. Решить уравнение: mх – 7 = — 1.

Если m = 0, то уравнение примет вид 0 • m= 6 и не имеет решений;

Если m ≠ 0, то уравнение примет вид х = и имеет единственное решение.

Ответ: при m= 0 нет решений; при m ≠ 0 х = .

№2. При каком значении b уравнение |х| + b = 0 не будет иметь корней?

Если b = 0, то уравнение примет вид |х| = 0, т.е. х = 0 и имеет ед. решение;

Если b > 0, то уравнение не имеет решений;

IV. Объяснение нового материала.

1. Определение линейного уравнения с параметром.

Уравнение вида Ах = В, (1)

где А, В — выражения, зависящие от параметров, ах- неизвестное,

называется линейным уравнением с параметрами.

2. что значит решить уравнение с параметрами?

Решить уравнение с параметрами — значит указать, при каких допустимых значениях параметров существуют решения, выяснить их число, каковы они; кроме того, обычно при решении уравнений с параметрами необходимо выяснить, при каких допустимых значениях параметров решений нет.

в) способы решения линейного уравнения.

Линейные уравнения с параметром решаются двумя способами: аналитическим и графическим.

Графический способ решения линейного уравнений с параметром удобен тогда, когда нужно определить количество корней уравнения.

Аналитический способ решения линейного уравнения с параметром удобен тогда, когда требуется найти решение уравнения при каждом значении параметра.

г) схема исследования линейного уравнения (1).

1. Если А = 0, В ≠ 0 , то уравнение (1) примет вид 0 • х = В и не имеет решений;

2. Если А = 0, В = 0, то уравнение (1) примет вид 0 • х = 0 и имеет бесконечное
множество решений (х — любое число);

3. Если А ≠ 0 , В — любое, то уравнение (1) имеет единственное решение

Замечание. Если линейное уравнение не представлено в виде (1), то сначала нужно привести его к виду (1) и только после этого проводить исследование.

V. Формирование умений и навыков учащихся.

№1. Решить уравнение: а) (а + 3)х =5.

Если а + 3 = 0, т.е. а = -3, то уравнение примет вид 0 • х = 5 и не имеет решений;

Если а + 3 ≠ 0 , т.е. а ≠ -3, то уравнение примет вид х = и имеет ед. решение.

Ответ: при а = -3 нет решений; при а ≠ -3 х = .

Если а – 6 = 0, т.е. а = 6, то уравнение примет вид 0 • х = -2 и не имеет решений;

Если а – 6 ≠ 0 , т.е. а ≠ 6, то уравнение примет вид х = и имеет ед. решение.

Ответ: при а = 6 нет решений; при а ≠ 6 х = .

№2. Решить уравнение: а) (а + 4)х = 2а +1.

Если а + 4 = 0, т.е. а = -4, то уравнение примет вид 0 • х = -7 и не имеет решений;

Если а + 4 ≠ 0, т.е. а ≠ -4, то уравнение примет вид х = и имеет ед. решение.

Ответ: при а = -4 нет решений; при а ≠ -4 х = .

Если а — 1 = 0, т.е. а = 1, то уравнение примет вид 0• х = -1 и не имеет решений;

Если а — 1 ≠ 0, т.е. а ≠ 1, то уравнение примет вид х = и имеет ед. решение. Ответ: при a = 1 нет решений; при а ≠ 1 х = .

№3. Решить уравнение: а) (а + 1)х = а + 1.

Если а + 1 = 0, т.е. а = -1, то уравнение примет вид 0 • х = 0 и имеет бесконечное множество решений (х — любое число);

Если а + 1 ≠ 0 , т.е. а ≠ -1, то уравнение примет вид х = , х = 1 и имеет ед. решение.

Ответ: при а = -1 х — любое число; при а ≠ -1 х = 1.

Если а – 4 = 0, т.е. а = 4, то уравнение примет вид 0 • х = 0 и имеет бесконечное множество решений (х — любое число);

Если а – 4 ≠ 0 , т.е. а ≠ 4, то уравнение примет вид х = , х = -1 и имеет ед. решение.

Ответ: при а = 4 х — любое число; при а ≠ 4 х = -1.

№4. Решить уравнение: а) (а – 7)х = а(а – 7).

Если а – 7 = 0, т.е. а = 7, то уравнение примет вид 0 • х = 0 и имеет бесконечное множество решений (х — любое число);

Если а – 7≠ 0 , т.е. а ≠ 7, то уравнение примет вид х = , х = а и имеет ед. решение.

Ответ: при a = 7 х — любое число; при а ≠ 7 х = а.

б) (а+5)х = (а + 5)(а – 2).

Если а + 5 = 0, т.е. а = -5, то уравнение примет вид 0 • х = 0 и имеет бесконечное множество решений (х — любое число);

Если а + 5 ≠ 0 , т.е. а ≠ -5, то уравнение примет вид х = ,

х = а – 2 и имеет ед. решение.

Ответ: при a = -5 х — любое число; при a ≠ -5 x = a – 2.

№5. Решить уравнение (а – 7)х = а 2 – 14а + 49.

Решение: (а – 7)х = (а – 7) 2 .

Если а – 7 = 0, т.е. а = 7, то уравнение примет вид 0 • х = 0 и имеет бесконечное множество решений (х — любое число);

Если а – 7 ≠ 0 , т.е. а ≠ 7, то уравнение примет вид х = , х = а – 7 и имеет единственное решение.

Ответ: при а = 7 х — любое число; при а ≠ 7 х = а – 7.

VI. Подведение итогов урока.

Что нового сегодня Вы узнали на уроке? Дайте определение линейного уравнения с параметрами. Что значит решить уравнение с параметром? Назовите способы решения и схему исследования линейного уравнения с параметром.

VII. Домашнее задание.

Решить уравнения: а) (а – 9)х = 4; б) (а – 6)х = а + 8; в) (а + 3)х = а + 3;

г) (а + 2)х = (а + 2)(а – 3); г) (а + 3)х = а 2 + 6а + 9.

Видео:Линейные уравнения с параметром 7-8 ые классыСкачать

По теме: методические разработки, презентации и конспекты

Разработка урока по алгебре в 9 классе «Системы уравнений с двумя переменными»

Предлагаю разработку обобщающего урока по алгебре в 9 классе. Тема: «Системы уравнений с двумя переменными», на данном уроке систематизируются знания по теме «Системы уравнений».

план урока по алгебре и началам анализа. показательные уравнение и неравенства

Урок по алгебре в 8 классе «Квадратное уравнение»

Урок проводится в конце изучения темы для закрепления навыков решения различных квадратных уравнений.

Урок итогового повторения в 9 классе» Линейные уравнения с параметром»

Рассмотрим уравнения, приводящиеся к линейным и дробно-линейным. Эти типы уравнений хорошо знакомы учащимся, и их решение не вызывает затруднений. Параметр, присутствующий в условии, не создает .

Урок по алгебре в 8 классе. Тема «Уравнение прямой вида y = kx + l».

Цели: Предментые: знать геометрический смысл коэффициентов к и l в уравнении прямой у = кх + l, уметь по уравнению прямой определять взаимное расположение графиков развив.

КОНСПЕКТ Урока по алгебре и началам математического анализа в 11 классе по теме «Решение показательных уравнений»

конспект урока по алгебре 8 класс по теме: «Уравнения, сводящиеся к квадратным. Биквадратные уравнения»

Конспект содержит историческую справку, материал для актуализации темы, разнообразные задания для работы в группах и индивидуально.

🔍 Видео

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Алгебра 7 класс (Урок№47 - Равносильность уравнений и систем уравнений.)Скачать

Уравнения с параметром. Алгебра, 8 классСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Алгебра 8 класс (Урок№33 - Уравнения с параметром. Контрольный урок.)Скачать

9 класс, 7 урок, Задачи с параметрамиСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Уравнения с модулем. Что такое модуль числа. Алгебра 7 класс.Скачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Простейшие уравнения с параметром #2Скачать

8 класс, 39 урок, Задачи с параметрамиСкачать

Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

Алгебра 7 Линейное уравнение с одной переменнойСкачать

Модуль выражения при решении уравнений. Алгебра 7 класс.Скачать

#1 КАК РЕШАТЬ ЗАДАЧИ С ПАРАМЕТРОМ. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМСкачать