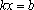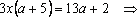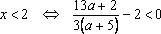Уравнения с параметрами 10 класс самостоятельные и контрольные работы

Видео:Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

Контрольные работы по спецкурсу для 10 класса «Уравнения и неравенства с модулем»
элективный курс по математике (10 класс) на тему

Контрольные работы полностью соответствуют Рабочей прграмме спецкурса по математике в 10 классе «Уравнения и неравенства с модулем» (2 часа в неделю)

Видео:Алгебра. 10 класс. Самостоятельные и контрольные работыСкачать

Скачать:

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Предварительный просмотр:

КИМы по спецкурсу для 10 КЛАССА

Всего контрольных работ – 6.

Контрольные работы полностью соответствуют плану спецкурсу.

КОНТРОЛЬНАЯ РАБОТА № 1 по теме «Модуль числа. Уравнения, содержащие модуль»

Контрольная работа № 1 состоят из 4 заданий в три варианта.

На оценку «5» — необходимо выполнить верно 4 заданий;

На оценку «4» — необходимо выполнить верно 4 заданий;

На оценку «3» — необходимо выполнить верно 3 заданий;

1.Проверить знания, умения их применять для выполнения учащимися:

а) упрощения иррациональных выражений, б) построения графиков функций;

в) решения уравнений.

2.Проверка уровня сформированности навыка решения различных заданий

по изученным темам.

3. Формировать вычислительные навыки учащихся.

Текст контрольной работы № 1.

1.Найти значение выражения:

2.Упростите выражение: а) ; б) ; в) .

3.Построить график функции: а) у = ; б) у = 2 . в) у = х 2 — 4 +3.

4. Решите уравнение: а) = 1; б) — =9; в) + = 6.

1. Найти значение выражения:

2.Упростите выражение: а) ; б) ; в) .

3.Построить график функции: а) у = ; б) у = 2 . в) у = х 2 — 6 + 5.

4. Решите уравнение: а) = 1; б) — =9; в) + = 6.

С/ р Неравенства с модулем

1. Неравенства вида «Модуль меньше функции»

1) . |2 x + 3| x +7 ; 2). | x ²+ 5 x | 3). | x 2 + 2 x -3| + 3( x +1)

4). | x 2 + 2 x – 7| x ; 5). | x 2 — x -1| x + 2 ; 6). | x 2 — 4 x – 4| x 2 — 4 ;

7) . | x 3 — 2 x -4| x — 4 .

2. Неравенства вида «Модуль больше функции»

1). |3 x +1| > 5 — 4 x ; 2). | x 2 + 2 x -3|> x ; 3). |2 x 2 — 9 x +15|> 20 ;

4). | x 2 — x -6 |> x +3; 5). | x 2 -8 x + 2|- x 2 > 2 x + 2 .

КОНТРОЛЬНАЯ РАБОТА № 2 по теме «Неравенства, содержащие модуль».

Контрольная работа № 2 состоят из 4 заданий в два варианта.

На оценку «5» — необходимо выполнить верно 4 заданий;

На оценку «4» — необходимо выполнить верно 4 заданий;

На оценку «3» — необходимо выполнить верно 3 заданий;

1.Проверить знания, умения их применять для выполнения учащимися:

а) упрощения иррациональных выражений, б) построения графиков функций;

в) решения уравнений.

2.Проверка уровня сформированности навыка решения различных заданий

по изученным темам.

3. Формировать вычислительные навыки учащихся.

Текст контрольной работы № 2.

1.Решить неравенства по определению: а) ; б)

3. При каких значениях х выражение | |x| -3x + 5| больше 3.

4. Найдите целые решения неравенства , решив его методом интервалов.

1.Решить неравенства: а) ; б) .

2. Решите неравенство ;

3. При каких значениях х выражение | |x| + 3x — 5| меньше 3.

4. Найдите целые решения неравенства: , решив его методом интервалов.

КОНТРОЛЬНАЯ РАБОТА № 3 по теме «Решение уравнений»

Контрольная работа № 3 состоят из 4 заданий в три варианта.

На оценку «5» — необходимо выполнить верно 4 заданий;

На оценку «4» — необходимо выполнить верно 3 заданий;

На оценку «3» — необходимо выполнить верно 3 заданий;

1.Проверить знания, умения их применять для выполнения учащимися:

а) решения уравнений: иррациональных, показательных, логарифмических,

б) нахождения частных решений тригонометрических уравнений.

2.Проверка уровня сформированности навыка решения различных заданий

по изученным темам.

3. Формировать вычислительные навыки учащихся.

Текст контрольной работы № 3.

1.Решите уравнения : а) ; б) ; в) .

2.Найдите наибольший корень уравнения : а) ;

3.Найдите корни уравнения : а) 2lg x = lg (6 – x) 2 ; б) lоg 4 (x 2 -15х ) = 2;

в) 2lоg 2 (-х) = 1 + lоg 2 (х + 4).

4.Решите уравнений: a) 2cos (x- ; б) sin 2 x — .

б) Найдите сумму корней уравнения (sin x + cos x) 2 = 1 + sin x∙ cos x, принадлежащие

1.Решите уравнения : а) ; б) ;

2.Найдите наибольший корень уравнения : а) ;

3.Найдите корни уравнения : а) 2lg x = lg (4 – x) 2 ; б) lоg 3 (x 2 — 6х ) = 3;

в) 2lоg 3 (-х) = 2 + lоg 3 (х — 2).

4.Решите уравнений: a) 2 sin (x — ; б) cos 2 x — .

б) Найдите сумму корней уравнения sin 4 x — cos 4 х = sin 2 x — 1, принадлежащие

КОНТРОЛЬНАЯ РАБОТА № 4 по теме «Общие методы решения уравнений».

Контрольная работа № 4 состоят из 4 заданий в три варианта.

На оценку «5» — необходимо выполнить верно 4 заданий;

На оценку «4» — необходимо выполнить верно 4 заданий;

На оценку «3» — необходимо выполнить верно 3 заданий;

1.Проверить знания, умения их применять для выполнения учащимися:

а) решения уравнений: иррациональных, показательных, логарифмических,

тригонометрических, используя общие методы решения уравненийю

б) нахождения частных решений тригонометрических уравнений.

2.Проверка уровня сформированности навыка решения различных заданий

по изученным темам.

3. Формировать вычислительные навыки учащихся.

Текст контрольной работы по теме «Общие методы решения

1.Решите уравнение: а) 25∙ ; б) х 2 + х + 2 + ;

2.Найдите количество корней уравнения: а) ;

б) 4 1-х + 4 х = 5, в) 3 ⋅ 4 х -5∙6 х + 2 ⋅ 9 х = 0.

3.Решите уравнения: а) lоg ( х — 1 ) ∙ lоg х = lоg х

б) lоg х + lоg х = 0; в) lоg (4 х ) — lоg х — 2= 0.

4. Решите уравнение а) sin 3x – sin x = 0; в) 1+ cos 4x = cos 2x;

и найдите его корни принадлежащие промежутку .

1.Решите уравнение: а) х 2 ∙ ; б) х 2 — х + ;

2.Найдите количество корней уравнения: а) ;

б) 2 х – 2 2-х = 3, в) 3 ⋅ 25 х — 8∙15 х + 5 ⋅ 9 х = 0.

3.Решите уравнения: а) lоg х = lоg ( х + 1 ) ∙ lоg х ;

б) lоg х — lоg х = 0; в) lоg (2 х ) +3 lоg х + 3= 0.

4. Решите уравнение а) cos 3x + cos x = 0; в) 1- cos 4x = sin 2x;

и найдите его корни принадлежащие промежутку .

КОНТРОЛЬНАЯ РАБОТА № 5 по теме «Неравенства».

Контрольная работа № 5 состоят из 4 заданий в три варианта.

На оценку «5» — необходимо выполнить верно 4 заданий;

На оценку «4» — необходимо выполнить верно 4 заданий;

На оценку «3» — необходимо выполнить верно 3 заданий;

1.Проверить знания, умения их применять для выполнения учащимися:

а) решения уравнений: иррациональных, показательных, логарифмических,

тригонометрических, используя общие методы решения уравненийю

б) нахождения частных решений тригонометрических уравнений.

2.Проверка уровня сформированности навыка решения различных заданий

по изученным темам.

3. Формировать вычислительные навыки учащихся.

Текст контрольной работы по теме «Неравенства».

1.Решите рациональное неравенство: а) 3х 2 – 2х – 8 > 0; б) ;

2.Решите показательное уравнение: а) 0,2 ; б) 3 х+1 ∙9 х-0,5 ;

в) 3 2х – 9 х-1 + 27 > 51.

3. решите логарифмическое уравнение : а) lоg (1 — 2х)

б) lоg 0,5 (1 + 2х) > -1; в) lоg 0,5 (х 2 – 5х + 6) > -1.

4. Решите неравенство методом интервалов: а) ; б) ;

в) (х 2 – 9) ∙ lоg 0,5 х

1. Решите рациональное неравенство: а) 2х 2 – 3х – 9 ;

2.Решите показательное уравнение: а) 0,5 ; б) 2 х-1 ∙4 х+0,5 ;

в) 2 2х – 4 х-1 + 8 14.

3. Решите логарифмическое уравнение : а) lоg (1 -3х)

б) lоg 0,5 (1 — 2х) > -2; в) lоg 0,5 (х 2 – 7х + 12) > -1.

4. Решите неравенство методом интервалов: а) ; б) ;

в) (х 2 – 16) ∙ lоg 0,2 х > 0.

КОНТРОЛЬНАЯ РАБОТА № 6 по теме «Решение заданий к ЕГЭ».

Контрольная работа № 6 состоят из 5 заданий в три варианта.

На оценку «5» — необходимо выполнить верно 5 заданий;

На оценку «4» — необходимо выполнить верно 5 заданий;

На оценку «3» — необходимо выполнить верно 5 заданий;

1.Проверить знания, умения их применять для выполнения учащимися:

а) решения уравнений: иррациональных, показательных, логарифмических,

тригонометрических, используя общие методы решения уравнений

б) решения неравенств: рациональных, показательных, логарифмических,

используя методы решения неравенств.

в) нахождения частных решений уравнений, неравенств

2.Проверка уровня сформированности навыка решения различных заданий

по изученным темам.

3. Формировать вычислительные навыки учащихся.

Текст контрольной работы № 6 будет составлен на основании сборника для подготовки к ЕГЭ за 2019г.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

По теме: методические разработки, презентации и конспекты

Линейные уравнения и неравенства с модулем. (факультативный курс, 8 класс)

Факультативный курс по алгебре для 8 класса.

Контрольно-обобщающий урок «Решение неравенств и систем неравенств с одной переменной»

Контрольно-обобщающий урок «Решение неравенств и систем неравенств с одной переменной». Цель урока: обобщение, систематизация и проверка знаний, умений и навыков в.

Тема 7. НЕРАВЕНСТВА С МОДУЛЕМ. ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА. Теория. Ключевые методы решения задач. Упражнения.

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, .

Итоговый контроль по темам № 6,7: «Алгебраические неравенства. Квадратные неравенства. Рациональные неравенства высших степеней. Дробно-рациональные неравенства. Неравенства с модулем. Иррациональные неравенства»

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, .

Тест по темам « Решение уравнений и их систем», «Решение неравенств и их систем» и «Решение уравнений, неравенств, систем неравенств с модулем».

Задания теста соответствуют содержанию учебника «Алгебра. 9 класс : учеб. для учащихся общеобразовательных учреждений / Ю. Н. Макарычев , Н. Г. Миндюк , К. И. Нешков , И. Е. Феоктист.

Модуль числа. Уравнения и неравенства содержащие модуль

В данной презентации вводиться понятие модуля числа, рассматриваются числовые промежутки.

презентация «Модуль числа. Уравнения и неравенства с модулем»

Презентация к уроку алгебры в 8 классе по учебнику Колягина М.Ю.

Видео:Уравнение с параметром | Математика TutorOnlineСкачать

Контрольная работа Уравнения 10 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Возвратные, обобщенные возвратные и симметрические уравнения:

Методом группировки x 3 – 7 x 2 – 21 x + 27 = 0

Используя Горнера 4 x 3 + x 2 – 5 = 0

Методом замены переменной x 4 + 2 x 3 – 9 x 2 – 6 x + 9 =0

Методом замены переменной x ( x – 1)( x – 2)( x – 3) = 8

Методом замены переменной (2 x – 1) 2 ( x + 2) 2 – (2 x – 1)( x 2 – 4) – 2( x – 2) 2 = 0

Найдите все значения b , при которых один из корней уравнения x 3 + 3 x 2 – bx – 8 = 0 равен. Для каждого из найденных значений b определите остальные корни уравнения.

Методом группировки 3 x 3 – 5 x 2 + 15 x – 81 = 0

Используя схему Горнера 2 x 3 – 3 x 2 – 4 x + 1 = 0

Методом замены переменной x 4 + 3 x 3 – 8 x 2 – 12 x + 16 = 0

Методом замены переменной x ( x + 2)( x + 3)( x + 5) = -5

Методом замены переменной (2 x + 1) 4 – (2 x 2 + 5 x + 2) 2 – 12( x + 2) 4 = 0

Найдите все значения b , при которых один из корней уравнения равен -2. Для каждого из найденных значений b определите остальные корни уравнения.

Методом группировки 3 x 3 – 5 x 2 + 15 x – 81 = 0

Используя схему Горнера 2 x 3 – 3 x 2 – 4 x + 1 = 0

Методом замены переменной x 4 + 3 x 3 – 8 x 2 – 12 x + 16 = 0

Методом замены переменной x ( x + 2)( x + 3)( x + 5) = -5

Методом замены переменной (2 x + 1) 4 – (2 x 2 + 5 x + 2) 2 – 12( x + 2) 4 = 0

Найдите все значения b , при которых один из корней уравнения равен -2. Для каждого из найденных значений b определите остальные корни уравнения.

Контрольная работа 2 10 класс

1)Методом группировки x 3 – 7 x 2 – 21 x + 27 = 0

2)Используя схему Горнера 4 x 3 + x 2 – 5 = 0

3)Симметрическое x 4 + 2 x 3 – 6 x 2 + 2 x + 1 =0

4)Методом замены переменной x ( x – 1)( x – 2)( x – 3) = 8 5)Однородное 2( x – 1) 2 – 5( x – 1)( x – 2) + 2( x – 2) 2 = 0

6)Решите систему уравнений

Методом группировки 3 x 3 – 5 x 2 + 15 x – 81 = 0

Используя схему Горнера 2 x 3 – 3 x 2 – 4 x + 1 = 0

Симметрическое x 4 — 4 x 3 +6 x 2 – 4 x + 1 = 0

Методом замены переменной x ( x + 2)( x + 3)( x + 5) = -5

Однородное (2 x + 1) 4 – ((2 x + 1)( x + 2)) 2 – 12( x + 2) 4 = 0

Решить систему уравнений

2х 2 – 3ху+ у 2 =0

7 Решить неравенство

Контрольная работа 2 10 класс

1)Методом группировки x 3 – 7 x 2 – 21 x + 27 = 0

2)Используя схему Горнера 4 x 3 + x 2 – 5 = 0

3)Симметрическое x 4 + 2 x 3 – 6 x 2 + 2 x + 1 =0

4)Методом замены переменной x ( x – 1)( x – 2)( x – 3) = 8 5)Однородное 2( x – 1) 2 – 5( x – 1)( x – 2) + 2( x – 2) 2 = 0

6)Решите систему уравнений

Методом группировки 3 x 3 – 5 x 2 + 15 x – 81 = 0

Используя схему Горнера 2 x 3 – 3 x 2 – 4 x + 1 = 0

Симметрическое x 4 — 4 x 3 +6 x 2 – 4 x + 1 = 0

Методом замены переменной x ( x + 2)( x + 3)( x + 5) = -5

Однородное (2 x + 1) 4 – ((2 x + 1)( x + 2)) 2 – 12( x + 2) 4 = 0

Решить систему уравнений

2х 2 – 3ху+ у 2 =0

7 Решить неравенство

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 700 человек из 76 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 860 человек из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 47 человек из 21 региона

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:Алгебра 10 класс (Урок№48 - Тригонометрические уравнения с параметрами.)Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 845 491 материал в базе

Материал подходит для УМК

«Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 25.10.2016
• 474
• 1

• 25.10.2016
• 518
• 0

• 25.10.2016
• 1125
• 0

• 24.10.2016
• 663
• 3

• 24.10.2016
• 996
• 8

• 24.10.2016
• 555
• 2

• 24.10.2016
• 451
• 0

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 25.10.2016 5359
• DOCX 48.5 кбайт
• 45 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Владимирова Алла Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 3 месяца
• Подписчики: 5
• Всего просмотров: 146166
• Всего материалов: 14

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Контрольная работа. Уравнения с МОДУЛЕМСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Роспотребнадзор сообщил об опасности размещения вышек сотовой связи на территории школ

Время чтения: 1 минута

Вузы РФ не будут повышать стоимость обучения на первом курсе

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Онлайн-семинар о здоровом образе жизни и организации секций

Время чтения: 2 минуты

Минобрнауки отменило плановые и внеплановые проверки вузов в 2022 году

Время чтения: 1 минута

Путин объявил 2022-2031 годы Десятилетием науки и технологий

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Контрольная работа 1Скачать

Задачи с параметрами для 10-11 класса

Задачи с параметрами

(10 – 11 классы)

Параметры – это те же числа, просто заранее не известные.

1. Линейные уравнения и неравенства с параметрами

Линейная функция: — уравнение прямой с угловым коэффициентом . Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси .

Линейные уравнения с параметрами

Если , уравнение имеет единственное решение.

Если , то уравнение не имеет решений, когда , и уравнение имеет бесконечно много решений, когда .

Пример 1. При всех значениях параметра а решить уравнение: (a2 – 4)x = a + 2

Решение: Разложим коэффициент при на множители. .

Если , уравнение имеет единственное решение: .

Если , уравнение не имеет решений.

Если , то уравнение имеет бесконечно много решений .

Пример 2. При всех значениях параметра а решить уравнение: .

Решение: ОДЗ: . При этом условии уравнение равносильно следующему: . Проверим принадлежность к ОДЗ: , если . Если же , то уравнениене имеет решений.

Пример 3. При всех значениях параметра а решить уравнение:

Решение: Разобьем числовую прямую на 3 части точками, в которых выражения под знаком модуля обращаются в нуль и решим 3 системы:

1) , если . Найденный будет решением, если .

2) , если . Найденный удовлетворяет нужному неравенству, следовательно, является решением при . Если же

, то решением является любой .

3) , если . Найденный не удовлетворяет нужному неравенству, следовательно, не является решением при . Если же

, то решением является любой . Сформируем

Ответ: при ; при ;

при ; является также решением при всех .

Пример 4. Найти все а , при каждом из которых хотя бы одно из решений уравнения 15x – 7a = 2 – 3ax + 6a меньше 2 .

Решение: Найдем решения уравнения при каждом . , если . Решим неравенство:

При уравнение не имеет решений.

Ответ: а Î (-5, 4).

Линейные неравенства с параметрами

Пример 1. Решить неравенство:

Если , то . Если , то . Если , то при решением является любой , а при решений нет.

Аналогично решите остальные неравенства в рамочке.

Пример 2. Для всех значений параметра а решить неравенство

Решение. . Если скобка перед положительна, т.е. при , то . Если скобка перед отрицательна, т.е. при

, то . Если же или , то решений нет.

Пример 3. Для всех значений параметра а решить неравенство

Просмотр содержимого документа
«Задачи с параметрами для 10-11 класса »

Параметры – это те же числа, просто заранее не известные.

1. Линейные уравнения и неравенства с параметрами

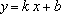
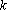
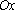
Линейная функция: — уравнение прямой с угловым коэффициентом . Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси .

Линейные уравнения с параметрами

Уравнение

Если 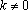, уравнение имеет единственное решение.

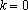
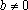
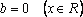
Если , то уравнение не имеет решений, когда , и уравнение имеет бесконечно много решений, когда .

Пример 1. При всех значениях параметра а решить уравнение: (a 2 – 4)x = a + 2

Решение: Разложим коэффициент при на множители. .

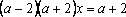
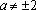
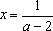
Если , уравнение имеет единственное решение: .

Если 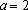, уравнение не имеет решений.

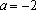
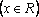
Если , то уравнение имеет бесконечно много решений .

Пример 2. При всех значениях параметра а решить уравнение: .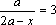

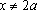
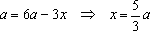
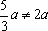
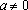
Решение: ОДЗ: . При этом условии уравнение равносильно следующему: . Проверим принадлежность к ОДЗ: , если . Если же , то уравнениене имеет решений.

Пример 3. При всех значениях параметра а решить уравнение:

Решение: Разобьем числовую прямую на 3 части точками, в которых выражения под знаком модуля обращаются в нуль и решим 3 системы:

1) , если . Найденный будет решением, если .

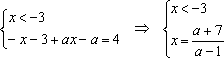
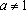
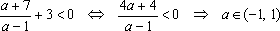
2) , если . Найденный удовлетворяет нужному неравенству, следовательно, является решением при . Если же

, то решением является любой .

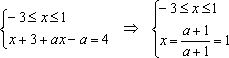
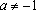
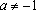
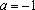
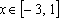
3) , если . Найденный не удовлетворяет нужному неравенству, следовательно, не является решением при . Если же

, то решением является любой . Сформируем

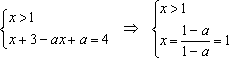
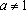
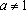
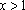
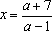
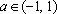
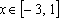
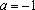
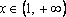
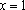
Ответ: при ; при ;

при ; является также решением при всех .

Пример 4. Найти все а , при каждом из которых хотя бы одно из решений уравнения 15x – 7a = 2 – 3ax + 6a меньше 2 .

Решение: Найдем решения уравнения при каждом . , если . Решим неравенство:

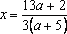
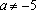
При уравнение не имеет решений.

Линейные неравенства с параметрами

Пример 1. Решить неравенство:

Если , то . Если , то . Если 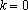, то при решением является любой , а при решений нет.

Аналогично решите остальные неравенства в рамочке.

Пример 2. Для всех значений параметра а решить неравенство

Решение. . Если скобка перед положительна, т.е. при , то . Если скобка перед отрицательна, т.е. при

, то . Если же или , то решений нет.

Пример 3. Для всех значений параметра а решить неравенство

Решение. При имеем неверное неравенство , т.е. решений нет. Пусть , тогда при оба модуля раскрываются с минусом и получаем неверное неравенство , т.е. решений нет. Если , то первый модуль раскрывается с минусом, а второй с плюсом и получаем неравенство , т.е. , т.е., решением является любой . Если оба модуля раскрываются с плюсом и получаем верное неравенство , т.е. , решением является любой . Объединяя оба ответа, получим, что при .

Пусть , тогда первое слагаемое больше, чем второе, поэтому разность в левой части неравенства положительна и, следовательно, не может быть меньше отрицательного числа . Т.о., при решений нет.

Ответ. При , при решений нет.

Замечание. Решении данной задачи получается быстрее и проще, если использовать геометрическую интерпретацию модуля разности двух чисел, как расстояние между точками. Тогда выражение в левой части можно интерпретировать, как разность расстояний от точки х до точек а и -а .

Пример 4. Найти все а , при каждом из которых все решения неравенства удовлетворяют неравенству .

Решение. Решением неравенства является множество , а решением неравенства является множество . Чтобы

удовлетворить условию задачи, нужно, чтобы множество А входило в множество В ( ). Это условие выполнится тогда и только тогда, когда

Пример 5. Найти все значения a , при которых неравенство выполняется для всех x из отрезка [1, 3] .

Решение. Дробь – меньше нуля между корнями, поэтому надо

выяснить, какой корень больше. и

. Т.о., при и чтобы неравенство выполнялось для всех x из отрезка [1, 3], нужно, чтобы

При и чтобы неравенство выполнялось для всех x из отрезка [1, 3], нужно, чтобы .

При (когда корни совпадают) решений нет, т.к. в этом случае неравенство приобретает вид : .

Пример 6. При каких значениях параметра а неравенство справедливо при всех отрицательных значениях х ?

Решение. Функция монотонно возрастает, если коэффициент при неотрицательный, и она монотонно убывает, если коэффициент при отрицательный.

Выясним знак коэффициента при . . .

Пусть . Тогда функция монотонно не убывает, и условие задачи будет выполнено, если

. Вместе с условиями получим : .

Пусть . Тогда функция монотонно убывает, и условие задачи никогда не может быть выполнено.

2. Векторы на плоскости

Пусть два вектора на плоскости заданы своими координатами:

Модуль (длина) вектора: .

где — угол между векторами.

Условие параллельности двух векторов: . Т.е.

у параллельных векторов координаты пропорциональны.

Условие перпендикулярности двух векторов: . Т.е. два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.

Если вектор задан своими концами и , то вектор .

Задача 1. Через точку провести прямую, параллельную вектору .

Решение. Пусть точка — текущая точка искомой прямой. Тогда вектор параллелен вектору . Тогда выписывая условие параллельности, получим уравнение искомой прямой:

Переписав в виде , получим уравнение с угловым коэффициентом , проходящей через заданную точку .

Задача 2. Через точку провести прямую, перпендикулярную вектору . Вектор , перпендикулярный прямой, называется нормальным вектором к прямой илинормалью к прямой.

Решение. Пусть точка — текущая точка искомой прямой. Тогда вектор перпендикулярен вектору . Тогда выписывая условие перпендикулярности, получим уравнение искомой прямой:

Раскрыв скобки и обозначив число , получим так называемое общее уравнение прямой:

В этом уравнении коэффициенты при и являются координатами нормального вектора прямой.

Всякая прямая разбивает плоскость на две полуплоскости, где с одной стороны прямой и с другой стороны. При этом точки той

части плоскости, куда смотрит вектор , удовлетворяет неравенству . Поэтому:

В направлении вектора функция возрастает, а в направлении вектора она убывает.

Пример 5. Написать уравнение прямой, проходящей через точку параллельно прямой .

Решение. У параллельных прямых нормальные вектора тоже параллельны, т.е. . Согласно задаче 2 получим искомое уравнение: или .

3. Системы двух линейных уравнений с параметрами

Решениями системы двух линейных уравнений являются точки пересечения двух прямых: и .

Возможны 3 случая:

1. Прямые не параллельны . Тогда и их нормальные вектора не параллельны, т.е. . В этом случае система имеет единственное решение.

2. Прямые параллельны и не совпадают. Тогда и их нормальные вектора параллельны, но сдвиги различны, т.е. .

В этом случае система решений не имеет .

3. Прямые совпадают. Тогда их нормальные вектора параллельны и сдвиги совпадают, т.е. . В этом случае система имеет бесконечно много решений – все точки прямой.

Пример 1. При всех значениях а и b решить систему уравнений

Решение. Выразим из первого уравнения и подставим во второе уравнение. Получим: .

Если — единственное решение. Если , то если , то решений бесконечно много: . Если

же , то решений нет.

Пример 2. При каком значении параметра а система уравнений

Решение. Система не имеет решений, если .

Пример 3. При всех значениях а решить систему уравнений

Решение. Система равносильна совокупности двух систем:

Прямые параллельны , если . При этом прямые не совпадают, поэтому при 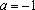решений нет.

Если 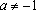, то выражая из второго уравнения и подставляя в первое, получим: .

Пример 4. Найти все такие значения а, что для любого значения b

найдётся хотя бы одно с такое, что система уравнений

имеет хотя бы одно решение.

Решение. Прямые не параллельны, если

В этом случае система имеет единственное решение при любом c.

По условию задачи система должна иметь решение при всех b.

Если то система принимает вид: . Чтобы при система также имела решения, нужно, чтобы уравнение относительно c имело хотя бы одно решение. Т.о., дискриминант этого уравнения должен быть неотрицательным, т.е.

Аналогично, если то система принимает вид: Чтобы при система также имела решения, нужно, чтобы уравнение

относительно c имело хотя бы одно решение. Т.о., дискриминант этого уравнения должен быть неотрицательным, т.е.

4. Системы двух линейных неравенств с параметрами

Пример 1. При каких значениях а система неравенств

не имеет решений?

Решение. Система имеет решения только если .

Ответ: при решением будет любой ;

при решений нет.

Пример 2. При каких значениях а система неравенств

имеет хотя бы одно решение?

Решение. При первое неравенство не имеет решений. А тогда и вся система не имеет решений.

Пусть , тогда и эта система не имеет решений, так как , а . Пусть , тогда т.е.

решения есть при , и , так как при выполнено неравенство , то решение запишется в виде .

Ответ: при решением будет любой ;

при решений нет.

Пример 3. При всех значениях а решить систему

Решение. Перепишем систему неравенств в виде . Рассмотрим все возможные случаи.

1) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем: при

2) . Тогда первое неравенство не верно. А значит, и вся система не имеет решений .

3) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем:

4) . Тогда второе неравенство не верно. А значит, и вся система не имеет решений .

5) . Тогда система неравенств принимает вид . Сравним между собой выражения в правых частях . Имеем: при

при и при решений нет.

Пример 4. При всех значениях а решить систему

При система не имеет решений.

Пусть , тогда и эта система не имеет решений.

Пусть , тогда и эта система будет иметь решения, если выполнено неравенство: .

💥 Видео

Разбор контрольной работы по алгебре 10 класс. Тригонометрические уравнения. МордковичСкачать

ЕГЭ №18 по математике. Задача с параметром. Параметры из реального ЕГЭ | TutorOnlineСкачать

Как решают уравнения в России и СШАСкачать

Уравнения с параметром. Алгебра, 8 классСкачать

Могу ли я подготовиться к профилю за ОСТАВШЕЕСЯ ВРЕМЯ | Аня МатеманяСкачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Простейшие уравнения с параметром #1Скачать

Алгебра 8 класс (Урок№33 - Уравнения с параметром. Контрольный урок.)Скачать

Простейшие уравнения с параметром #2Скачать

Уравнения с параметрами | Алгебра 11 класс #32 | ИнфоурокСкачать

Физика 10 класс. Самостоятельные и контрольные работы (базовый уровень)Скачать