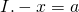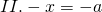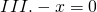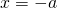Уравнения с отрицательными числами 6 класс примеры с ответами (6 видео)

Сложение отрицательных чисел

Содержание

Что такое отрицательные числа
Сложение отрицательных чисел
Описание алгоритма
Примеры задач с ответами для 6 класса
Уравнения вида -х равен a
Уравнения с отрицательными числами 6 класс примеры с ответами
Основные правила математики с примерами. 6 класс. Часть 2.
Содержание
💥 Видео

Видео:Решение уравнений с отрицательными числами.Скачать

Что такое отрицательные числа

Отрицательное число является компонентом множества из отрицательных чисел, сформированного в процессе увеличения множества натуральных чисел.

Расширение спектра натуральных чисел потребовалось для зачисления операции вычитания в перечень полноценных арифметических действий таких, как сложение. При рассмотрении натуральных чисел можно заметить, что вычитание предполагает всегда уменьшение большего числа на меньшее число. Переместительный закон на действия с вычитанием не распространяется.

Вычитать можно любые натуральные числа, так как к натуральным числам добавили отрицательные числа и нуль. В итоге такой трансформации получилось множество, которое состояло из целых чисел. В дальнейшем числовые множества пополнились за счет рациональных и вещественных чисел, которые также могут обладать отрицательными значениями. Понятие отрицательного числа не применимо к комплексным числам.

Рассмотрим числовую ось, на которой отмечены отрицательные числа с левой стороны от нуля:

Любое натуральное число n имеет единственное отрицательное число, которое обозначают, как -n, дополняющее n до нуля:

Такие числа являются противоположными. Одни числа называют положительными, а в противовес им существуют отрицательные числа. В том случае, когда n представляет собой положительное число, можно сказать, что противоположное ему число является отрицательным. Заметим, что нуль противоположен сам себе.

Таким же способом можно определить положительные и отрицательные значения, когда вопрос касается рациональных и вещественных чисел: какому-либо положительному числу a противопоставляется отрицательное число -a.

Положительные и отрицательные числа упорядочены, поэтому данные числа можно сравнивать между собой. Все отрицательные числа меньше по сравнению с нулем, а также меньше по сравнению с положительными числами. Рассматривая числовую ось, можно заметить, что они расположены слева по отношению к нулю.

Абсолютная величина для числа a является этим числом с отброшенным знаком и обозначается a .

Если число a вычитается из другого числа b, то данное действие будет равносильным сумме b с противоположным числом для a:

25 – 75 = 25 + ( — 75 ) = — 50

Видео:Решение уравнений, 6 классСкачать

Сложение отрицательных чисел

Существует несколько способов сложения отрицательных чисел. К примеру, если числа по модулю обладают небольшими значениями, допускается использование координатной прямой. При этом можно представить действия, как перемещение точки, обозначающей число, по числовой оси.

Предположим, что имеется некое число 3 и отметим его на числовой оси в виде точки А.

Попробуем увеличить число 3 на положительное число 2, то есть найдем их сумму. В процессе требуется передвинуть точку А в положительном направлении на пару единичных интервалов. При перемещении в правую сторону будет установлена точка В с координатой 5.

Далее разберем пример сложения положительного и отрицательного числа:

При этом требуется точку А передвинуть на 5 отрезков в отрицательном направлении, то есть в левую сторону. Заметим, что тогда точка В будет установлена в координате -2.

Алгоритм действий при сложении рациональных чисел с использованием координатной прямой:

Отметить на числовой прямой точку А с координатой в виде первого слагаемого.
Переместить точку А на количество отрезков в соответствии с модулем второго слагаемого. Если второе слагаемое имеет знак плюса, то движение происходит в правую сторону. Когда у слагаемого знак минус, точка перемещается в левую сторону.
Полученная в результате точка В обладает координатой, равной сумме рассматриваемых чисел.

Разберем процесс сложения двух отрицательных чисел:

Переместим точку с позиции -2 в левую сторону, получим -8:

Упрощенным вариантом сложения рациональных чисел является применение модуля. Рассмотрим способ на конкретном примере. Предположим, что имеются два числа с одинаковыми знаками и найдем их сумму.

В первую очередь следует избавиться от знаков и суммировать модули чисел. К результату нужно дописать знак, который фигурировал в исходной записи чисел:

4 8 + 3 8 = 4 + 3 8 = 7 8

Разберем на примере сложение отрицательных чисел аналогичным способом:

( — 3 , 2 ) + ( — 4 , 3 ) = — ( 3 , 2 + 4 , 3 ) = — 7 , 5

Сложение чисел с одинаковыми знаками предполагает сложение модулей этих чисел и запись перед полученной суммой знака, который стоял перед слагаемыми.

Таким образом, можно вывести правило для сложения отрицательных чисел.

Найти сумму пары отрицательных чисел можно путем сложения их модулей. Перед результатом, который получился, нужно поставить знак минуса.

Видео:Уравнения с отрицательными числами (Математика 6 класс)Скачать

Описание алгоритма

Алгоритм сложения двух отрицательных чисел, в том числе, в виде дробей:

сложение модулей чисел;
постановка знака минуса перед числом, полученным в результате вычислений.

Применим алгоритм действий при выполнении упражнения:

В первую очередь сложим модули заданных чисел и перед полученным числом запишем знак минуса:

— 24 + ( — 16 ) = — ( 24 + 16 ) = — 40

Видео:Как вычитать отрицательные числа? / Простые примеры из жизни по математикеСкачать

Примеры задач с ответами для 6 класса

Требуется решить примеры:

Воспользуемся правилом сложения чисел с разными знаками и алгоритмом сложения отрицательных чисел. Получим:

4 + ( — 5 ) = 4 — 5 = — 1

( — 17 ) + ( — 45 ) = — 17 — 45 = — 62

— 9 + ( — 1 ) = — 9 — 1 = — 10

Ответ: -1; -21; -62; -10.

Необходимо выполнить вычисления:

Согласно алгоритму сложения отрицательных чисел, выполним арифметические действия:

3 — ( — 6 ) = 3 + 6 = 9

— 27 — ( — 5 ) = — 27 + 5 = — 22

— 94 — ( — 61 ) = — 94 + 61 = — 33

Ответ: 9; -51; -22; -33.

Сложить два отрицательных числа:

Руководствуясь правилом сложения отрицательных чисел, найдем сумму их модулей:

| — 304 | + | — 18007 | = — | 18311 |

Запишем ответ со знаком минуса:

( — 304 ) + ( — 18007 ) = — ( 304 + 18007 ) = — 18311

Видео:Все действия с отрицательными числами за 2 минутыСкачать

Уравнения вида -х равен a

Уравнения вида «-x равен а» появляются в 6 классе с началом изучения отрицательных чисел.

Поскольку такие уравнения в дальнейшем будут встречаться довольно часто, желательно сразу же научиться их решать правильно и быстро.

В общем виде уравнения вида «минус икс равен а» можно разбить на три случая:

Рассмотрим каждый из вариантов в общем виде и на примерах.

Решить это уравнение — значит, найти x. x и -x — противоположные числа. Поэтому икс равен числу, противоположному числу, стоящему в правой части уравнения, то есть числу которое отличается только знаком:

Рассуждая аналогично, приходим к выводу, что

Здесь минус икс равен нулю. Нуль не является ни положительным, ни отрицательным числом и противоположен самому себе, поэтому корень этого уравнения

Итак, в общем виде решение уравнений вида минус икс равен а можно записать так:

Видео:Сложение и вычитание рациональных чисел. 6 класс.Скачать

Уравнения с отрицательными числами 6 класс примеры с ответами

Математику уж затем учить надо, что она ум в порядок приводит

Основные правила математики с примерами. 6 класс. Часть 2.

Содержание

Умножение. Свойства умножения

Произведением числа на натуральное число не равное 1, называют сумму, состоящую из слагаемых, каждое из которых равно а:

a · b = a + a + a + . . . + a ⏟ b

Если один из двух множителей равен 1, то произведение равно второму множителю:

Если один из множителей равен нулю, то произведение равно нулю:

Если произведение равно нулю, то хотя бы один из множителей равен нулю.

!Важное правило. Помогает решать уравнения

( x — a ) ( x — b ) = 0 ; И л и x — a = 0 , и л и x — b = 0 ; 2 к о р н я x = a и x = b . ( x — 5 ) ( x + 2 ) = 0 ; И л и x — 5 = 0 , и л и x + 2 = 0 ; 2 к о р н я x = 5 и x = — 2 .

Умножение обыкновенных дробей

Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:

Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Умножение рациональных чисел

Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».

Чтобы умножить два отрицательных числа, надо умножить их модули.

Для любого рационального числа :

Если произведение • — отрицательное, то числа и имеют разные знаки.

Деление обыкновенных дробей

Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:

a b : c d = a b · d c

Деление рациональных чисел

Чтобы найти частное двух чисел с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».

Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.

Нахождение дроби от числа

Чтобы найти дробь от числа, можно число умножить на эту дробь.

Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.

Нахождение числа по его дроби

Чтобы найти число по значению его дроби, можно это значение разделить на эту дробь.

Найти число, если известно, что

е г о д р о б ь 5 7 с о с т а в л я е т ч и с л о 15 : 15 : 5 7 = 15 · 7 5 = 15 3 · 7 5 1 = 21

Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь.

Найти число, если известно, что

24 % э т о г о ч и с л а р а в н ы 48 . 24 % = 24 100 ; 48 : 24 100 = 48 · 100 24 = 48 2 · 100 24 1 = 200

Степень числа

Степенью числа с натуральным показателем , большим , называют произведение множителей, каждый из которых равен :

a n = a · a · a · … · a ⏟ n

Число при этом называют основанием степени.

Степенью числа с показателем называют само число

Вторую степень числа называют также квадратом числа. Например, запись читают: « в квадрате».
Третью степень называют кубом числа, а запись читают: « в кубе».

Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а затем производят другие действия.

Найти значение выражения

5 · 2 3 + 15 5 · 2 2 3 1 + 3 15 = 5 · 8 + 15 = 40 + 15 = 55

Числовые и буквенные выражения

Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением.

Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.

Приведение подобных слагаемых

Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.

Раскрытие скобок

Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.

Если перед скобками стоит знак « + », то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.

Свойства уравнений

Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.

Если данное уравнение не имеет корней, то, прибавив к обеим его частям одно и то же число, получим уравнение, тоже не имеющее корней.

Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.

Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.

Отношения

Частное двух чисел и , не равных нулю, еще называют отношением чисел и , или отношением числа к числу .

Отношение положительных чисел и показывает, во сколько раз число больше числа , или какую часть число составляет число .

показывает, что число 10 в 5 раз больше числа 2 или число 2 в 5 раз меньше числа 10.

Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Пропорции

Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:

a : b = c : d и л и a b = c d

Числа и называют крайними членами пропорции, а числа и — средними членами пропорции.

Основное свойство пропорции

Произведение крайних членов пропорции равно произведению ее средних членов:

a b = c d ⇒ a d = b c

Если , , и числа, не равные нулю, и • = • , то отношения

могут образовывать пропорцию

Процентное отношение двух чисел

Процентное отношение двух чисел — это их отношение, выраженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.

Прямая и обратная пропорциональная зависимость

Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.

Если величины и обратно пропорциональны, то их соответствующие значения удовлетворяют равенству