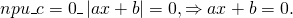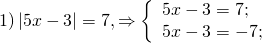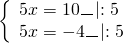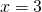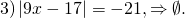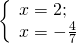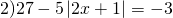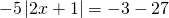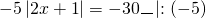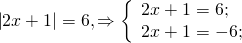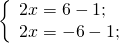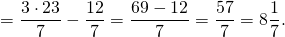Разделы: Математика
Класс: 6
Тип урока: урок постановки учебной задачи.
Цели урока:
- обучение решению уравнений со знаком модуля на основе применения свойств уравнений;
- развитие навыков теоретического мышления с применением навыков элементарных операций с модулем и определения модуля;
- воспитание внимания и умения анализировать полученное решение, участвовать в диалоге с товарищами, учителем.
I. Повторение пройденного
Внимательно рассмотрите предложенные уравнения:
1) | х | = х + 5;
2) | х | = – 3х + 5;
3) | х – 3 | = 2;
4) | 2х – 5 | = х – 1;
5)= х – 1;
6) | 2х – 5 | = 2 – х;
7) | х + 2 | = 2(3 – х);
8) | 3х – 5 | = | 5 – 2х | ;
9) | х – 2 | = 3 | 3 – х | ;
10) | | х – 1 | – 1 | = 2.
Задание 1. Распределите данные уравнения по группам.
Учащиеся сначала выделили две группы. В первую группу вошли уравнения 1) –3), 5) –7). Ко второй группе были отнесены уравнения 8) и 9). Затем учащиеся заметили уравнение 10), содержащее знак модуля два раза. Окончательно было выделено три группы: 1-я группа – модуль содержится в левой части уравнения; 2-я группа – модуль содержится в обеих частях уравнения; 3-я группа – в уравнении содержится двойной модуль.
Учитель. Какую главную задачу мы должны будем решить сегодня на уроке?
Учащиеся. Мы должны научиться решать уравнения.
Учитель. Да. Но посмотрите еще раз на все эти уравнения и выделите их общую особенность.
Учащиеся. Все они содержат модуль.
Учитель. Как точнее сформулировать задачу нашего урока?
Учащиеся. Применять определение модуля при решении данных уравнений.
Учитель. Действительно, эту задачу мы и должны решить на уроке. По-другому ее можно сформулировать так: “Как решать уравнения с модулем?” Какие понятия, определения могут быть полезны при решении этой задачи?
1. Что такое модуль?
2. Определение модуля.
Учитель. Вспомним, что такое модуль.
Учащиеся. По определению:
| а | =  | если а > 0 если а 0 (число положительное).
а) Если х – 3 Содержание Видео:6 класс. Решение уравнений с модулями.Скачать  Уравнения с модулями — Материалы для подготовки к самостоятельным работамПример 1. Решим уравнение: а) Модуль числа равен 3 лишь в двух случаях: если это число равно либо -3, либо 3: |2x — 1| = 3, 1) 2x — 1 = -3 или 2) 2x — 1 = 3. Решив каждое из этих уравнений, получим, что корень уравнения 1) равен -1, а корень уравнения 2) равен 2. Следовательно, уравнение |2х — 1| = 3 имеет два корня: -1 и 2. б) Так как ни при каком значении x модуль числа не равен отрицательному числу, то уравнение |7х — 8| = -3 не имеет корней. в) Модуль числа равен 0 лишь в одном случае: если это число равно 0. Ответ. а) -1; 2; б) нет корней; в) Пример 2. Решим уравнение 8 — |5x — 7| = 1. Решение. Прибавим к обеим частям уравнения число -8: Умножим обе части уравнения на число -1: |5x — 7| = 7. Модуль числа равен 7 лишь в двух случаях: если это число равно либо -7, либо 7: 1) 5х — 7 = -7 или 2) 5х — 7 = 7. Решив каждое из этих уравнений, получим, что корень уравнения 1) равен 0, а корень уравнения 2) равен Ответ. Пример 3. Решим уравнение ||х — 12| — 2| = 5. Решение. Модуль числа равен 5 лишь в двух случаях: если это число равно либо -5, либо 5: Уравнение 1) не имеет корней, так как ни при каком значении х модуль числа не равен отрицательному числу. Чтобы решить уравнение 2), надо найти корни каждого из уравнений: 3) х — 12 = 7 и 4) х — 12 = -7. Решив каждое из этих уравнений, получим, что корень уравнения 3) равен 19, а корень уравнения 4) равен 5. Пример 4. Решим уравнение |||2х + 5| + 2| — 5| = 6. Решение. Заметим, что для любого значения х число |2х + 5| + 2 положительно, поэтому данное уравнение можно переписать в виде ||2х + 5| — 3| = 6. Модуль числа равен 6 лишь в двух случаях: если это число равно либо -6, либо 6: Уравнение 1) не имеет корня, так как ни при каком значении х модуль числа не равен отрицательному числу. Чтобы решить уравнение 2), надо найти корни каждого из уравнений: 3) 2х + 5 = -9 и 4) 2х + 5 = 9. Решив каждое из этих уравнений, получим, что корень уравнения 3) равен -7, а корень уравнения 4) равен 2. Следовательно, уравнение |2х + 5| — 3 = 6 имеет два корня: -7 и 2. Значит, и уравнение |||2x + 5| + 2| — 5| = 6 имеет два корня: -7 и 2. Библиотека образовательных материалов для студентов, учителей, учеников и их родителей. Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями. Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта. Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид. © 2014-2022 Все права на дизайн сайта принадлежат С.Є.А. Видео:Модуль числа. Практическая часть. 6 класс.Скачать  Уравнения с модулем в 6 классеУравнения с модулем в 6 классе сводятся к простейшим уравнениям, решение которых опирается на определение модуля. Рассмотрим некоторые из таких уравнений. Начнем с такого вида: Решаем это уравнение как линейное: неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки: Теперь обе части уравнения делим на число, стоящее перед модулем икса: Данное уравнение не имеет решений, так как модуль не может быть отрицательным числом. Ответ: нет решений. Также в 6 классе встречаются уравнения с модулем вида Это уравнение — почти простейшее уравнение с модулем, соответственно, решаем его аналогично: Каждое из полученных уравнений — линейное. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки: Более сложные уравнения с модулем в 6 классе представляют собой сочетание обоих видов. Сначала рассмотрим это уравнение как линейное (все выражение, стоящее под знаком модуля, считаем одним неизвестным): Данное уравнение решим как простейшее уравнение с модулем: Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать  141 Commentsя ещё не разу не пользовалась этим сайтом Очень хороший сайт… реально помог Помогите решить,пожалуйста, -|х|=3 -|х|=3 Помогите решить, пожалуйста: |х|-2= -3 |х|= -3 + 2; |х|= -1. Нет решений, так как модуль не может быть равным отрицательному числу. Будьте добры, объясните решение примера с модулем в модуле: PS. х в квадрате. |-|3-х²||=6; |3-х²|=6; 3-х²=±6; 3-х²=6 или 3-х²=-6; х²=-3 или х²=9. Первое из уравнений не имеет корней, корни второго — x=3 и x=-3. Помогите решить уравнение пожалуйста 3|x+4|-7=18 3|x+4|=18+7; 3|x+4|=25; |x+4|=25/3; x+4=±8 1/3 помогите решить задачи модуль х=1 модуль выражения х-3=1 модуль х=х Если |х|=1, то х=1 или х=-1. Спасибо вам очень сильно помогло.Вседа были проблемы, а сейчас нету Бексултан, если все новые темы разбирать по мере изучения, проблем не будет. Учитесь, и всё у Вас получится! Помогите, пожалуйста, (3+|x|)(4-2|x|)=0 Это уравнение типа произведение равно нулю. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый их множителей:3+|x|=0 или 4-2|x|=0. Отсюда |x|=-3 или 2|x|=4, |x|=2. Уравнение |x|=-3 не имеет корней, уравнение |x|=2 имеет два корня: х=2 и х=-2. Помогите пожалуйста решить: 0,63:|x|=0,91; |x|=0,63:0,91; |x|=9/13: х=9/13 или х= -9/13. Помогите ещё, пожалуйста,вот это |5х+2|-11=21 |5х+2|=21+11; |5х+2|=32; 5х+2=32 или 5х+2=-32; 5х=30, х=6 или 5х=-34, х=-6,8. Помогите пожалуйста решить x=9 или x=-9. Помогите решить пожалуйста: А что, собственно, требуется найти? Найти чему равно А , а то есть решить уравнение Получается, что у Вас в одном уравнении две переменные ещё и х. Нужно либо еще одно уравнение, либо Вы что-то в условии напутали. Это пример, который дан в тесте Что-то не то с условием. Может, пришлёте фото задания? 1)Если х≥0, то |х|=х и уравнение принимает вид х²=-4х, корни которого равны 0 и -4. Условию х≥0 удовлетворяет только х=0. -|x|=10-7 Помогите пожалуйста-x=9 и второе -x=-3 Если -x=a, то x=-a. Помогите, пожалуйста, решить Модуль (х+Y)=0 Лилия, решить это уравнение не получится. Можно сказать только, что если модуль x+y равен нулю, то и x+y=0, а значит, x=-y, то есть x и y — противоположные числа. Помогите решить |||2х+7|-3|+6=6 Одна скобка лишняя. ||2х+7|-3|=6-6; ||2х+7|-3|=0;|2х+7|-3=0; |2х+7|=3. Далее — 2 варианта: Помогите пожалуйста решить 7,4-3,6|x|=18-4|x| Помогите решить 0x=8 помогите решить |x|-6=-9 |x|=-9+6 Помогите решить пожалуйста 2|x|+|1-3x| при x=1,2 Это же не уравнение. Просто подставляем вместо x 1,2 и вычисляем: Помогите решить 3|х-6|+4у,если х= две целых 5/7,у=-3/7 Олеся, Вы вполне можете найти значение этого выражения самостоятельно. Нужно просто подставить вместо x и y их значения: помогите решить |5x+1|=3 Антон, ведь сверху есть аналогичные примеры. Один раз разберитесь, и проблем с такими заданиями больше не будет. Помогите решить 3х-2|у-1| при х=-1, у=-4 и объясните как вы решили Вместо x и y подставляем их значения х=-1, у=-4: Помогите решить Здесь можно только упростить.Так как |-x|=|x|, то x-4=2 или x-4= -2. Решаем оба уравнения по отдельности. Получаем два корня: Помогите решить |3x + 2 | = | x — 1 | Самый простой способ решения уравнений такого вида — возвести обе части уравнения в квадрат (если Вы уже знаете, как решаются квадратные уравнения). Помогите решить Умножим обе части уравнения на -1: Помогите решить Так как |-4|=4, то уравнение сводится к уравнению |x|=4, откуда x=4, x=-4. Помогите пожалуйста! |x|= -x.Это равенство верно для любого неположительного числа (то есть x≤0). Памагите решить. /2х/-y=0 y=4 Подставив вместо y 4, получаем уравнение |2х|-4=0. Отсюда |2х|=4; 2х=4 или 2х=-4. //а+5/-а/ при том что а=-6. помогите пожалуйста помогите пожалуйста 5|x|=4,2 |x|= 4,2:5 Здравствуйте, помогите решить пожалуйста уравнение: Можно рассмотреть 2 варианта раскрытия модулей. Помогите пожалуйста решить (a-3)(a+2)x=a+2 Это — линейное уравнение. Уравнение вида ax=b при a≠0 имеет единственный корень x=b/a. Помогите придумать уровнение с модулем из 6 класса Помогите пожалуйста решить Если x Олег 15.02.2019 17:31 Ответить Помогите решить уравнение ||x|-9|=3. ||x|-9|=3 помогите пожалуйста 7х+4|x|=-3 1) если x>0, |x|=x Помогите пожалуйста решить:||x|-5|||=6 Артём, у Вас знаков модуля больше, чем нужно:||x|-5|=6 Можно пожалуйста обьеснить чему равно N если N Светлана Михайловна 27.05.2019 20:06 Ответить Условие N Захар 27.05.2019 20:37 Ответить помогите пожалуйста решить −21:|x|=0,04−7,04. Антон, а давайте Вы попробуете решить этот пример самостоятельно, а я его проверю. Если будут ошибки, помогу. Идёт? ответ будет x1=-3 x2=3 ? Антон, обе части линейного уравнения делим на число, стоящее ПЕРЕД иксом. Огромное спасибо я понял что я сделал не так Антон, успехов Вам в изучении математики! Не бойтесь решать самостоятельно и делать ошибки. Это же учёба. А вот если ничего не делать, то не получится научиться. помогите пожалуйста решить 3|x-2|-|2-x|/-3=-5,2 Татьяна, |2-x|/(-3)? Для начала Вам подсказка: |a-b|=|b-a| спасибо я уже решила Можно еще вопрос-нужно найти значение выражения х*|у| если х=-2, у=-3/4 Модуль отрицательного числа равен противоположному числу. Например, |-9|=9. Дальше — дело техники. Успехов Вам в учёбе, Татьяна! Используйте время карантина наилучшим образом. Помогите пожалуйста решить уравнение -|0.7|•у=|0.42| Помогите решить (|7,6|-|-8,1|):|-5| Добрый вечер, помогите решить ||x|-5|=6 ||x|-5|=6 Здравствуйте, уважаемая Светлана Михайловна! Помогите, пожалуйста разобраться. Ребенок на вступительном тестировании в лицей решал пример: 3-|4|x|-7|=-4^2 (четыре в квадрате, но с минусом большой вопрос: что тут имелось в виду — квадрат числа с минусом? Тогда, может, скобки должны были быть? Или просто ребенок неправильно переписал пример). Что Вы скажете по поводу решения данного примера? Во-первых, если бы в квадрат возводили -4, то обязательно должны быть скобки. Спасибо огромное за разъяснение и за этот сайт! Очень помогает вспомнить свою школьную программу и прояснить все узкие места для современных школьников :)). СПАСИБО! Ольга, Вам спасибо за теплые слова! Здравствуйте, помогите пожалуйста решить уравнение с модулями /5-/4x-7//*(2x+19)=0 Светлана Михайловна, помогите решить уравнение. |7x-57,1|-|-14/3|=|31/3| Помогите, пожалуйста: Найдите значение выражения: | — 4 | + |1 – 3х| , при х = 2,4. Здравствуйте, помогите пожалуйста решить уравнение с модулем |4-|1-2x||=22 4-|1-2x|=22 или 4-|1-2x|=-22 Здравствуйте Помогите решить пример Объясните пожалуйста как решать: 4(y+1)-3|x+5| при x: 7, y: -2 Подставляем x=7 и y=-2 в данное выражение: Помогите пожалуйста с уравнение |3х+2|=|х-1| заранее спасибо! Самый простой способ — возвести в квадрат обе части и решить полученное квадратное уравнение. В 6 классе квадратных уравнений решать ещё не умеем, действуем иначе. Каждый модуль можно раскрыть с знаками плюс и минус. Таким образом, получаем 2 случая: если знаки модулей одинаковы и если они разные. помогите решить |6+5x|=2 и еще один |8-|x+2||=7 1)|6+5x|=2 Почему |x|=10, то x=-10;x=10 Богдан, потому что модуль числа a — это расстояние от начала отсчёта (точки О с координатой 0) до точки с координатой а. На координатной прямой на расстоянии 10 от нуля находятся две точки — точка с координатой 10 и точка с координатой -10. Помогите пожалуйста решить 3•|0,2х+4|-3=-5,4 3∙|0,2х+4|=-5,4+3; 3∙|0,2х+4|=-2,4; |0,2х+4|=-2,4:3; |0,2х+4|=-0,8. Нет решений, так как модуль не может быть отрицательным. 🎥 ВидеоЛинейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать  Контрольная работа. Уравнения с МОДУЛЕМСкачать  Модуль числа. Практическая часть. 6 класс.Скачать  Уравнения с модулемСкачать  Как решать уравнения с модулем ( Математика 6 класс )Скачать  Уравнения с модулем. Математика 6 классСкачать  Уравнения с модулем. Что такое модуль числа. Алгебра 7 класс.Скачать  Уравнения с модулем 🫢Скачать  Как решать уравнение с модулем Уравнение с модулями как решать Как раскрыть модуль в уравненииСкачать  Уравнение с модулемСкачать  6 класс, 24 урок, Модульные уравнения и неравенства с одной переменнойСкачать  Модуль числа, 6 классСкачать  Модуль числа. 6 класс.Скачать  уравнение с модулем за 60 секундСкачать  Решение уравнений с модулем в 6 классеСкачать  КАК РЕШАТЬ УРАВНЕНИЯ С МОДУЛЕМ (КОЭФФИЦИЕНТОВ)? Примеры | МАТЕМАТИКА 6 классСкачать  ВПР 6 КЛАСС. Задание с модулем.Скачать  |
 = х – 1;
= х – 1; 
 0, то есть х
0, то есть х  3, то | х – 3 | = х – 3;
3, то | х – 3 | = х – 3; Следовательно, уравнение 8 — |5x — 7| = 1 имеет два корня:
Следовательно, уравнение 8 — |5x — 7| = 1 имеет два корня: 



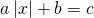
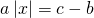
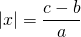
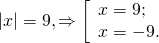

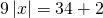
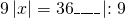
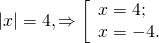
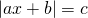
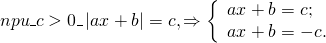 0_left| right| = c, Rightarrow left< begin ax + b = c;\ ax + b = — c. end right.]» title=»Rendered by QuickLaTeX.com»/>
0_left| right| = c, Rightarrow left< begin ax + b = c;\ ax + b = — c. end right.]» title=»Rendered by QuickLaTeX.com»/>