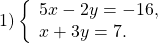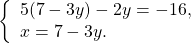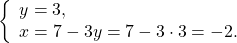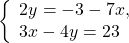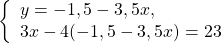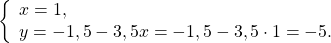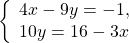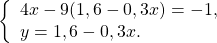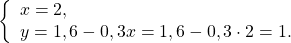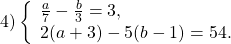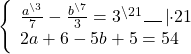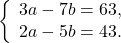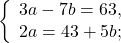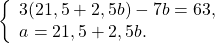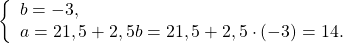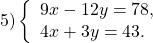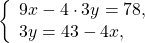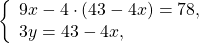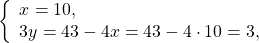- Алгоритм решения системы линейных уравнений методом подстановки
- Примеры
- Примеры решения систем линейных уравнений методом подстановки
- Алгоритм решения систем уравнений методом подстановки и сложения .Алгебра 7 класс. тренажёр по алгебре (7 класс) на тему
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Как репетитор по математике работает с методом подстановки в системах уравнений (7 класс)
- Как репетитор по математике работает с трудными темами?
- Подготовительная работа репетитора
- Что чаще всего не понятно ученику?
- 🔍 Видео
Алгоритм решения системы линейных уравнений методом подстановки
- Из любого уравнения системы выразить одну переменную через другую.
- Подставить во второе уравнение системы вместо переменной выражение, полученное на первом шаге.
- Решить второе уравнение относительно выраженной переменной.
- Подставить найденное значение переменной в выражение, полученное на первом шаге.
- Найти значение второй переменой.
- Записать ответ в виде упорядоченной пары найденных значений переменных.
Из второго уравнения выражаем y:
Подставляем выражение для y в первое уравнение:
Шаг 3 Решаем первое уравнение:
Подставляем значение x в выражение для y:
В последовательной записи:
$$ <left< begin 3x+y = 5 \ y-x = 1 end right.> Rightarrow <left< begin 3x+y = 5 \ y = x+1 end right.> Rightarrow <left< begin 3x+(x+1) = 5 \ y = x+1 end right.> Rightarrow <left< begin 4x = 5-1 \ y = x+1 end right.> Rightarrow $$ $$ Rightarrow <left< begin x = 1 \ y = x+1 end right.> Rightarrow <left< begin x = 1 \ y = 2end right.> $$
Примеры
Пример 1. Решите систему уравнений методом подстановки:
$ а) <left< begin 5x-4y = 3 \ 2x-3y = 4 end right.> Rightarrow <left< begin 5x-4y = 3 \ x = frac = 1,5y+2 end right.> Rightarrow <left< begin 5(1,5y+2)-4y = 3 \ x = 1,5y+2 end right.> Rightarrow $
$ Rightarrow <left< begin 7,5y+10-4y = 3 \ x=1,5y+2 end right.> Rightarrow <left< begin 3,5y = -7 \ x = 1,5y+2 end right.> Rightarrow <left< begin y = -2 \ x = 1,5y+2 end right.> Rightarrow <left< begin x = -1 \ y = -2end right.> $
$ б) <left< begin 4x-3y = 7 \ 3x-4y = 0 end right.> Rightarrow <left< begin 4x-3y = 7 \ y = frac x end right.> Rightarrow <left< begin 4x-3cdot frac x = 7 \ y = frac x end right.> Rightarrow <left< begin (4- frac)x = 7 \ y = frac x end right.> Rightarrow $
$Rightarrow <left< begin x = 7 cdot frac = 4 \ y = frac x = frac cdot 4 = 3 end right.> Rightarrow <left< beginx = 4 \ y = 3 end right.> $
$ в) <left< begin 5a-4b = 9 \ 2a+3b = -1 end right.> Rightarrow <left< begin 5a-4b = 9 \ a = frac = -1,5b-0,5 end right.> Rightarrow <left< begin 5(-1,5b-0,5)-4b = 9 \ a = -1,5b-0,5 end right.> Rightarrow $
$ Rightarrow <left< begin -7,5b-2,5-4b = 9 \ a = -1,5b-0,5 end right.> Rightarrow <left< begin-11,5b = 11,5 \ a = -1,5b-0,5 end right.> Rightarrow <left< begin a = 1 \ b = -1 end right.> $
$ г) <left< begin 7a+4b = 5 \ 3a+2b = 1 end right.> Rightarrow <left< begin 7a+4b = 5 \ b = frac = -1,5a+0,5 end right.> Rightarrow <left< begin 7a+4(-1,5a+0,5) = 5 \ b = -1,5a+0,5 end right.> Rightarrow $
$ Rightarrow <left< begin 7a-6a+2 = 5 \ b = -1,5a+0,5 end right.> Rightarrow <left< begin a = 3 \ b = -1,5cdot3+0,5 = -4 end right.> $
Пример 2. Найдите решение системы уравнений:
$а) <left< begin frac-y = 7 | times 4 \ 3x+ frac = 9 | times 2end right.> Rightarrow <left< begin x-4y = 28 \ 6x+y = 18 end right.> Rightarrow <left< begin x = 4y+28 = 4(y+7) \ 6 cdot 4(y+7)+y = 18 end right.> Rightarrow $
$Rightarrow <left< begin x = 4(y+7) \ 24y+168+y = 18 end right.> Rightarrow <left< begin x = 4(y+7) \ 25y = -150 end right.> Rightarrow <left< beginx = 4(-6+7) = 4 \ y = -6 end right.>$
$ в) <left< begin 3(5x-y)+14 = 5(x+y) \ 2(x-y)+9 = 3(x+2y)-16 end right.> Rightarrow <left< begin 15x-3y+14 = 5x+5y \ 2x-2y+9 = 3x+6y-16 end right.> Rightarrow $
$ Rightarrow <left< begin 10x-8y = -14 |:2 \ x+8y = 25 end right.> Rightarrow <left< begin 5x-4y = -7 \ x = -8y+25 end right.> Rightarrow <left< begin 5(-8y+25)-4y = -7 \ x = -8y+25 end right.> Rightarrow $
$ Rightarrow <left< begin -40y+125-4y = -7 \ x = -8y+25 end right.> Rightarrow <left< begin -44y = -132 \ x = -8y+25 end right.> Rightarrow <left< begin x = 1 \ y = 3 end right.> $
$ г) <left< begin 5-3(2x+7y) = x+y-52 \ 4+3(7x+2y) = 23x end right.> Rightarrow <left< begin 5-6x-21y = x+y-52 \ 4+21x+6y = 23x end right.> Rightarrow <left< begin 7x+22y = 57 \ 2x-6y = 4 |:2 end right.>$
$$ Rightarrow <left< begin 7x+22y = 57 \ x-3y = 2 end right.> Rightarrow <left< begin 7x+22y = 57 \ x = 3y+2 end right.> Rightarrow <left< begin 7(3y+2)+22y = 57 \ x = 3y+2 end right.> Rightarrow $$
$$ Rightarrow <left< begin 21y+14+22y = 57 \ x = 3y+2 end right.> Rightarrow <left< begin 43y = 43 \ x = 3y+2 end right.> Rightarrow <left< begin x = 5 \ y = 1 end right.>$$
Пример 3*. Найдите решение системы уравнений:
Перепишем систему и найдём решение для новых переменных:
$$ <left< begin 3a+8b = 5 \ 12b-a = 2 end right.> Rightarrow <left< begin 3(12b-2)+8b = 5 \ a = 12b-2 end right.> Rightarrow <left< begin 36b-6+8b = 5 \ a = 12b-2 end right.> Rightarrow $$
Видео:Урок по теме СПОСОБ ПОДСТАНОВКИ 7 классСкачать

Примеры решения систем линейных уравнений методом подстановки
Рассмотрим конкретные примеры решения систем линейных уравнений методом подстановки.
В данном случае удобно из второго уравнения системы выразить x через y и подставить полученное выражение вместо x в первое уравнение:
Первое уравнение — уравнение с одной переменной y. Решаем его:
Полученное значение y подставляем в выражение для x:
В данной системе проще из первого уравнения выразить y через x и подставить полученное выражение вместо y во второе уравнение:
Второе уравнение — уравнение с одной переменной x. Решим его:
В выражение для y вместо x подставляем x=1 и находим y:
Здесь удобнее из второго уравнения выразить y через x (поскольку делить на 10 проще, чем на 4, -9 или 3):
Решаем первое уравнение:
Подставляем x=2 и находим y:
Прежде чем применить метод подстановки, эту систему следует упростить. Обе части первого уравнения можно умножить на наименьший общий знаменатель, во втором уравнении раскрываем скобки и приводим подобные слагаемые:
Получили систему линейных уравнений с двумя переменными. Теперь применим подстановку. Удобно из второго уравнения выразить a через b:
Решаем первое уравнение системы:
3(21,5 + 2,5b) — 7b = 63
Осталось найти значение a:
Согласно правилам оформления, ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.
Выражая одну переменную через другую, иногда удобнее оставлять её с некоторым коэффициентом.
В данном случае удобно выразить y через x из второго уравнения. При этом лучше не делить обе части уравнения на 3, а оставить коэффициент 3 рядом с y, поскольку в первом уравнении 12y кратно 3:
Из всех способов решения систем уравнений метод подстановки в алгебре используется чаще других. С помощью этого метода могут быть решены не только системы линейных уравнений, но и системы уравнений других видов.
Видео:Решение систем уравнений методом подстановкиСкачать

Алгоритм решения систем уравнений методом подстановки и сложения .Алгебра 7 класс.
тренажёр по алгебре (7 класс) на тему
Алгоритм решения систем уравнений методом подстановки и сложения .Алгебра 7 класс.Подробное пошаговое описание работы для слабоуспевающих учащихся с тренировочными заданиями.
Видео:Решение систем уравнений. Методом подстановки. Выразить YСкачать

Скачать:
| Вложение | Размер |
|---|---|
| sistemy_uravneniy.metod_podstanovki.docx | 18.82 КБ |
| sistemy_uravneniy.metod_slozheniya.docx | 18.84 КБ |
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Предварительный просмотр:
Образец решения системы уравнений методом подстановки
АЛГОРИТМ (последовательность шагов при работе)
Выразить из первого уравнения у через х, т.е.перенести 3х в другую часть с противоположным знаком ( т.к. у записан в уравнении без числа(коэффициента)). Получится у = 7 – 3х
у = 7 – 3х
Выделить в рамочку выраженную переменную у . Написать её в той же строчке в системе уравнений.
у = 7 – 3х
— 5х + 2(7 – 3х) = 3
Подставить во второе уравнение вместо у выражение ( 7 – 3х), взяв его в скобки !
Приготовить знак системы уравнений и место для будущих ответов х у
-5х + 2·(7 – 3х) = 3
«Выйти из системы» и решить отдельно только уравнение с одной переменной х : 1) раскрыть скобки, умножив число перед скобкой на всё что в скобках;
-5х + 14 -6х = 3
2) Перенести число 14 в правую часть уравнения с противоположным знаком, т.е. сделать «сортировку» — буквы к буквам, числа к числам.
3) Посчитать значение в левой и правой части уравнения
4) Вычислить х как неизвестный множитель, вспомнив простой пример 2 · 3 = 6
Заполнить место в системе уравнений для х
у = 7 – 3х = 7 — 3·1 = 7-3 = 4
Найти значение второй переменной у
Заполнить место в системе уравнений для у
Записать ответ в виде координат точки (х;у)
Решить систему уравнений методом подстановки
выбирая удобную переменную для её выражения, когда она записана без числа.
№1. у – 2х = 1 №4. 2х + у = 12
6х – у = 7 7х – 2у = 31
№2. х + у =6 №5. 4х – у = 11
3х – 5у = 2 6х – 2у = 13
№3. 7х – 3у = 13 №6. 8у – х = 4
х – 2у = 5 2х – 21у = 2
Карточка составлена учителем математики Головлянициной Лидией Вадимовной
Видео:Решение систем линейных уравнений методом подстановки (видеоурок) - 7 класс алгебраСкачать

Предварительный просмотр:
Рассмотрим коэффициенты перед х и у. Удобно сделать перед переменной у противоположные коэффициенты 2 и -2.
4х + у = 3 |·2
Для этого умножим правую и левую часть первого уравнения на 2, а второе уравнение оставим без изменения.
8 х + 2 у = 6
6у – 2у = 1
Поставим знак «+» между уравнениями слева и проведем черту,
как при сложении столбиком по разрядам.
8 х + 2 у = 6
6х – 2у = 1
Сложим подобные 8х и 6х получим 14х .Запишем это число под чертой. Подобные 2у и -2у взаимно уничтожаются и зачёркиваются. Справа (после равно) складываем числа 6 и 1 и результат записываем под чертой.
Находим х по правилу нахождения неизвестного множителя.
Теперь осталось вычислить у . Выбираем и записываем то уравнение из системы, где у стоит без коэффициента, т.е. коэффициент равен 1 .
Подставить вместо х значение 0,5. Решить уравнение, сделав перенос числа 2 в правую часть с противоположным знаком.
Ответ: х = 0,5; у = 1
Пользуясь этим алгоритмом, решите системы уравнений:
- 3х – у = 7
- 2х + 3у = 1 Карточка составлена учителем математики Головлянициной Лидией Вадимовной
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

По теме: методические разработки, презентации и конспекты
Решение систем уравнений методом подстановки 7 класс
Решение систем уравнений методом подстановки 7 класс.
Решение систем уравнений (метод подстановки)
УНЗ представлен в виде межпредметного урока, интегрированного урока, метапредметного урока (материал находится в разработке).
Урок алгебры 7 класс Решение систем уравнений методом подстановки
Тип урока: урок рефлексии.Технология: урок разработан в системе традиционного обучения с опорой на технологию деятельностного метода.Цель урока: создать условия для повторения и закрепления алгоритма .
Урок на тему «Решение систем уравнений способом подстановки и способом сложения».
Урок изучения новой темы в компетентностно- констектной модели обучения и воспитания (первый этап всей изучаемой темы).
План-конспект урока “Решение систем уравнений” (способ подстановки и способ сложения)
Приводится план-конспект урока алгебры в 9 классе.
Презентации по теме «Системы двух линейных уравнений», «Метод подстановки для решения систем уравнений», «Метод сложения для решения систем уравнений» .
Презентации проедполагает использование при проведении онлайн урока по теме «Системы двух линейных уравнений», «Метод подстановки для решения систем уравнений», «Метод сложени.
Методическая разработка. Презентация по алгебре 7 класс по теме «Решение систем уравнений методом сложения»
В презентации рассмотрены несколько примеров рассуждения и оформления систем уравнений методом сложения. Материал можно использовать во время дистанционного обучения.
Видео:Алгебра 7 класс. Решение систем уравнений методом подстановкиСкачать

Как репетитор по математике работает с методом подстановки в системах уравнений (7 класс)
И зучение математики в 7 классе принципиально отличается от всего того, что предлагалось ранее в 5 — 6 классах. И дело не только в названиях тем и разделении предмета на алгебру и геометрию. Помимо введения новых понятий и правил меняется характер работы с числами и выражениями. Многое из того, что репетитор по математике показывает в 7 классе является обобщением ранее пройденного, но поднимающее использование математики на принципиально новый уровень. Такое продвижение предполагает прочное усвоение вычислительной базы, которое к 7 классу должно быть достигнуто. Должно, но не обязано.
Значительные пробелы отстающих школьников, обращающихся к репетитору по математике в тот или иной период учебы в школе, ставят неразрешимые проблемы перед использованием традиционных методик объяснений, а именно методик прямого изложения материала. Креативный репетитор по математике находится в постоянном поиске новых форм и способов подачи объяснений конкретному ученику. И это очень непросто сделать.
Как репетитор по математике работает с трудными темами?
Трудность каждой конкретной темы — весьма относительное понятие. Все зависит от того, с какой стороны к ней подойти и насколько ученик способен воспринимать ту или иную форму объяснений репетитора. Многие сложные понятия упрощаются, если репетитору по математике удается подобрать какое-нибудь простое и лаконичное описание математического процесса, сравнить его с чем-то обыденным и понятным, связать новое с ранее изученным. Это непростая задача, но репетитору нужно стремиться к ее выполнению. В алгебре, при объяснении нового материала, бывает достаточно точно подобрать соответствующие примеры работы правила на числах. У многих учеников 7 класса все еще преобладает тип мышления «от общего к частному», поэтому, стремление репетитора по математике к абсолютной стрости и полноте объяснений (доказательств), к использованию общих форм, рассмотрению всех случаев или педантичной проверке равносильности в переходах может перечеркнуть все усилия по обеспечению понимания.
Важно добиться первоначального понимания, пусть ученику не открывается вся картина происходящего в алгоритме, а лишь приоткрывается некая завеса нового. В некоторых случаях уже одно такое продвижение можно ставить в заслугу репетитору по математике, ибо ребенок начинает хоть что-то решать самостоятельно. Это крайне важно, ибо результаты практической работы помогает осмыслить многие моменты, которые оказались непонятыми.
Иногда репетиторы по математике, особенно начинающие, путают два состояния ученика: не понял и не запомнил. Если ребенок говорит «я не понимаю», — это не всегда означает, что слова репетитора по математике остались не осмысленными. Часто бывает наоборот: заявляет, что все понятно, но на проверку оказывается, что он просто заучил те или иные ходы в решении. Репетитору важно уметь отличать эти два состояния и правильно их использовать.
Как правило, решение систем методом подстановки вызывает у детей 7 класса дикое отвращение и неприязнь. Почему? Процесс, который описывает репетитор по математике на первом уроке по данной теме, очень трудно увязывается с привычным занятием в алгебре 7 класса. Дети настолько привыкают к однострочным одношаговым решениям (какими являются преобразования многочленов). Поэтому, когда репетитор по математике исписывает равносильными системами целую страницу в тетради, ученик почти всегда заявляет: «я не понимаю». «Стоп! Давай разберемся», — говорю я ему. Что именно из этого ты не понял, а что просто не успел запомнить? Если репетитор по математике поставит вопрос именно таким ребром, он переводит деятельность ученика из созерцательной в оценочную. Нужно дать время на то, чтобы привыкнуть к записям и запомнить ходы. Это облегчит оценку того, что именно не понятно. Главное не торопить ученика и дать ему возможность высказаться. Пусть это будут невнятные фразы, лишенные логики. Мастерство репетитора заключается в том, чтобы выявить проблему даже по «обрывкам мыслей» ученика.
Конечно, я описываю ситуацию, в которой репетитор не провел с учеником соответствующую подготовительную работу. А она обязательно нужна.
Подготовительная работа репетитора
Нужны задания на проверку конкретных пар чисел для конкретной системы. В процессе выполнения простейших заданий репетитор обкатывает новую терминологию: пара чисел, удовлетворяющая системе, решение системы, проверка пары. Я еще употребляю фразы «вставка чисел», «вставка пары»
Важно убедить ученика в том, что совсем не обязательно искать пару чисел, которая при вставке в начальную систему даст два верных равенства. Мы же ищем саму пару.
Самому слабому ученику достаточно сказать, что при замене одной системы на другую не меняется самое главное — ее ответ, поэтому не важно, какую именно систему решать. Пара, подходящая для одной из них — подойдет и для другой. Это можно просто проверить на конкретных числах. Надо чувствовать ученика и не ввязываться в объяснения равносильности переходов в 7 классе, какими бы точными они не были. Если все-таки репетитор по математике хочет донести до сознания ученика логику алгоритма, это нужно делать после того, как ученик его запомнит.
Если ученик более-менее толковый, репетитор по математике применяет числовую методику проверки равносильности. Покажу ее работу на примере
Пусть задана система линейных уравнений:
Как ее решить — все вы отлично знаете. Но как объяснить это решение слабому учащемуся? Вот она — головная боль для преподавателя. Дети в 7 классе не воспринимают общие математические методы доказательства равносильности, под лупой которых, конечно же, вся логика преобразований оказывается на поверхности.
Какие методики могут быть задействованы в принципе? Обычно репетитор по математике проводит равносильные преобразования по классической схеме:
Однако нельзя оставлять такую форму без каких-либо объяснений.
Что чаще всего не понятно ученику?
Как правило к моменту изучения темы «метод подстановки», учащиеся 7 класса уже имеют выражать переменную y через переменную x. Будем считать, что репетитор по математике решил эту проблему в теме «графический способ решения систем уравнений». Тогда самый непонятный ход — вставка выражения 3-x во второе уравнение системы на место x.
Как репетитор может объяснить замену игрека на 3-x ?
Я покажу как можно работать со средним учеником по методике числовой проверки ( если ученик сильный — для него вполне подойдут строгие математические обоснования «в обе стороны»). Итак, рассмотрим равносильный переход между системами:
Надо убедить ученика в том, что одна и та же пара чисел (она предоставляется в готовом виде) превращает каждое равенство в верное. Репетитор говорит: «Давай проверим пару (2;1), то есть х=2; y=1. Вставим их на места букв в систему (1).Получим: 

Остальные равносильные преобразования репетитору по математике не составит труда объяснить. В них нет ничего нового. Обычное решение уравнения с одной переменной. Понятно, что икс должен быть корнем уравнения (2). Ученики в 7 классе обычно понимают, что его надо найти.
Замечу, что ответ нужно записывать не в виде x=2; y=1, а в виде пары (2;1). Это будет способствовать скорейшему формированию у ученика представления об ответе, как о некоторой точке координатной плоскости.
Репетитор по математике 7 класс — Колпаков А.Н. Москва, Строгино.
🔍 Видео
ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Решение систем уравнений методом сложенияСкачать

7 класс, 38 урок, Метод подстановкиСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать

Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать

Способ подстановки. Алгебра. 7 класс.Скачать

Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

7 класс, 39 урок, Метод алгебраического сложенияСкачать

решение системы уравнений методом подстановки 7 классСкачать

Алгебра 7 класс. 28 октября. Решаем систему уравнений методом сложения #2Скачать