Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.
Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.
Видео:Математика #1 | Корреляция и регрессияСкачать

Введение в регрессионный анализ
Если имеется корреляционная зависимость между переменными y и x , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения
называется регрессией y по x .
Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей
минимальна.
Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.
Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений
вокруг регрессии
является дисперсия.
- k — число коэффициентов в системе уравнений регрессии.
Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x .
Линейная регрессия
Уравнения линейной регрессии можно записать в виде
В матричном виде это выгладит
- y — зависимая переменная;
- x — независимая переменная;
- β — коэффициенты, которые необходимо найти с помощью МНК;
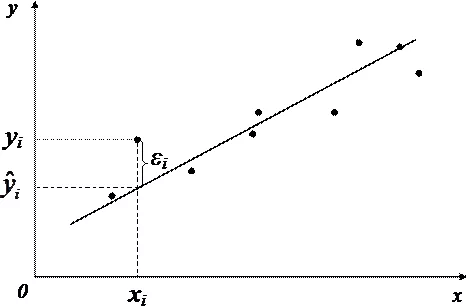
- ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;
Случайная величина может быть интерпретирована как сумма из двух слагаемых:
— полная дисперсия (TSS).
— объясненная часть дисперсии (ESS).
— остаточная часть дисперсии (RSS).
Еще одно ключевое понятие — коэффициент корреляции R 2 .
Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Ограничения линейной регрессии
Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.
- Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз.
- Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы.
- Экзогенность независимых переменных —
. Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных.
- Однородность дисперсии и отсутствие автокорреляции. Каждая εi обладает одинаковой и конечной дисперсией σ 2 и не коррелирует с другой εi. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована.
Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.
Неоднородность дисперсии
При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.
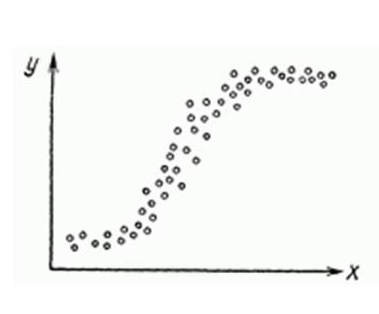
Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.
Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.
- Автокорреляция проверяется статистикой Дарбина-Уотсона (0 ≤ d ≤ 4). Если автокорреляции нет, то значения критерия d≈2, при позитивной автокорреляции d≈0, при отрицательной — d≈4.
- Неоднородность дисперсии — Тест Уайта,
, при
chi_$» data-tex=»inline»/> нулевая гипотеза отвергается и констатируется наличие неоднородной дисперсии. Используя ту же
можно еще применить тест Бройша-Пагана.
- Мультиколлинеарность — нарушения условия об отсутствии взаимной линейной зависимости между независимыми переменными. Для проверки часто используют VIF-ы (Variance Inflation Factor).
В этой формуле — коэффициент взаимной детерминации между
и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.
Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.
Видео:Выбор факторов, влияющих на результативный показательСкачать

Как преодолеть эти ограничения
Нарушения одной или нескольких ограничений еще не приговор.
- Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln .
- Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln , или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК.
- Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы.
К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.
Видео:Корреляционно-регрессионный анализ. ЭтапыСкачать
Линейная регрессия плюсов на Хабре
Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.
Загружает данные из tsv файла.
- points — Рейтинг статьи
- reads — Число просмотров.
- comm — Число комментариев.
- faves — Добавлено в закладки.
- fb — Поделились в социальных сетях (fb + vk).
- bytes — Длина в байтах.
Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.
Теперь собственно сама модель, используем функцию lm .
В первой строке мы задаем параметры линейной регрессии. Строка points
. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points
reads , набор переменных — points
Перейдем теперь к расшифровке полученных результатов.
- Intercept — Если у нас модель представлена в виде
, то тогда
— точка пересечения прямой с осью координат, или intercept .
- R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
- Adjusted R-squared — Проблема с
в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации .
- F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
- t value — Критерий, основанный на t распределении Стьюдента . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели.
- p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.
Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.
Проверим значения параметров линейной регрессии.
Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми , F-статистика выросла, так же как и скорректированный коэффициент детерминации .
Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.
И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.
Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

В заключение
Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.
Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.
Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Корреляция и регрессия
Линейное уравнение регрессии имеет вид y=bx+a+ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид:
10a + 356b = 49
356a + 2135b = 9485
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 68.16, a = 11.17
Уравнение регрессии:
y = 68.16 x — 11.17
1. Параметры уравнения регрессии.
Выборочные средние.
1.1. Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 Y фактором X весьма высокая и прямая.
1.2. Уравнение регрессии (оценка уравнения регрессии).
Линейное уравнение регрессии имеет вид y = 68.16 x -11.17
Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент уравнения регрессии показывает, на сколько ед. изменится результат при изменении фактора на 1 ед.
Коэффициент b = 68.16 показывает среднее изменение результативного показателя (в единицах измерения у ) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 68.16.
Коэффициент a = -11.17 формально показывает прогнозируемый уровень у , но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений x , то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения x , можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и x определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:
Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами — Х существенно влияет на Y.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего Y на 0.9796 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве регрессии.
1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.98 2 = 0.9596, т.е. в 95.96 % случаев изменения x приводят к изменению у . Другими словами — точность подбора уравнения регрессии — высокая. Остальные 4.04 % изменения Y объясняются факторами, не учтенными в модели.
| x | y | x 2 | y 2 | x·y | y(x) | (yi— y ) 2 | (y-y(x)) 2 | (xi— x ) 2 | |y — yx|:y |
| 0.371 | 15.6 | 0.1376 | 243.36 | 5.79 | 14.11 | 780.89 | 2.21 | 0.1864 | 0.0953 |
| 0.399 | 19.9 | 0.1592 | 396.01 | 7.94 | 16.02 | 559.06 | 15.04 | 0.163 | 0.1949 |
| 0.502 | 22.7 | 0.252 | 515.29 | 11.4 | 23.04 | 434.49 | 0.1176 | 0.0905 | 0.0151 |
| 0.572 | 34.2 | 0.3272 | 1169.64 | 19.56 | 27.81 | 87.32 | 40.78 | 0.0533 | 0.1867 |
| 0.607 | 44.5 | .3684 | 1980.25 | 27.01 | 30.2 | 0.9131 | 204.49 | 0.0383 | 0.3214 |
| 0.655 | 26.8 | 0.429 | 718.24 | 17.55 | 33.47 | 280.38 | 44.51 | 0.0218 | 0.2489 |
| 0.763 | 35.7 | 0.5822 | 1274.49 | 27.24 | 40.83 | 61.54 | 26.35 | 0.0016 | 0.1438 |
| 0.873 | 30.6 | 0.7621 | 936.36 | 26.71 | 48.33 | 167.56 | 314.39 | 0.0049 | 0.5794 |
| 2.48 | 161.9 | 6.17 | 26211.61 | 402 | 158.07 | 14008.04 | 14.66 | 2.82 | 0.0236 |
| 7.23 | 391.9 | 9.18 | 33445.25 | 545.2 | 391.9 | 16380.18 | 662.54 | 3.38 | 1.81 |
2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=7 находим tкрит:
tкрит = (7;0.05) = 1.895
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
В парной линейной регрессии t 2 r = t 2 b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S 2 y = 94.6484 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
Sy = 9.7287 — стандартная ошибка оценки (стандартная ошибка регрессии).
S a — стандартное отклонение случайной величины a.
Sb — стандартное отклонение случайной величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bxp ± ε) где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 1 (-11.17 + 68.16*1 ± 6.4554)
(50.53;63.44)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bx i ± ε)
где
| xi | y = -11.17 + 68.16xi | εi | ymin | ymax |
| 0.371 | 14.11 | 19.91 | -5.8 | 34.02 |
| 0.399 | 16.02 | 19.85 | -3.83 | 35.87 |
| 0.502 | 23.04 | 19.67 | 3.38 | 42.71 |
| 0.572 | 27.81 | 19.57 | 8.24 | 47.38 |
| 0.607 | 30.2 | 19.53 | 10.67 | 49.73 |
| 0.655 | 33.47 | 19.49 | 13.98 | 52.96 |
| 0.763 | 40.83 | 19.44 | 21.4 | 60.27 |
| 0.873 | 48.33 | 19.45 | 28.88 | 67.78 |
| 2.48 | 158.07 | 25.72 | 132.36 | 183.79 |
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (7;0.05) = 1.895
Поскольку 12.8866 > 1.895, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 2.0914 > 1.895, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — tкрит Sb; b + tкрит Sb)
(68.1618 — 1.895 • 5.2894; 68.1618 + 1.895 • 5.2894)
(58.1385;78.1852)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a — ta)
(-11.1744 — 1.895 • 5.3429; -11.1744 + 1.895 • 5.3429)
(-21.2992;-1.0496)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с lang=EN-US>n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=7, Fkp = 5.59
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.
Обнаружение автокорреляции
1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения ei с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения ei (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости ei от ei-1.
Видео:Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Корреляционный и регрессионный анализ.
Корреляционный анализ — это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами.
Регрессионный анализ — это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами.
Корреляционный анализ — дает возможность рассчитывать уровень доверия к результатам анализа. В процессе этого анализа рассчитываются показатели корреляции, к которым относятся коэффициенты корреляции и корреляционные отношения. При сравнении функциональных и корреляционных зависимостей следует иметь в виду, что при наличии функциональной зависимости между признаками можно, зная величину факторного признака, точно определить величину результативного признака. При наличии же корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака. В отличие от жесткости функциональной связи корреляционные связи характеризуются множеством причин и следствий и устанавливаются лишь их тенденции. Простейшим приемом обнаружения связи является сопоставление двух параллельных рядов. Из общего анализа видно, что увеличение количества промоакций способствует увеличению объема продаж. Характер распределения указывает на то, что объем сбыта растет по мере увеличения количества промоакций. Следовательно, имеется положительная связь между факторами. Регрессионный анализ даст возможность ответить на вопрос о количественной мере влияния различных факторов, например на спрос (объем возможной продажи). Он представляет собой подбор и решение математических уравнений, описывающих исследуемые зависимости. Элементы рынка зависят от многих факторов, и формы этих зависимостей могут быть самыми разнообразными. Поэтому регрессионный анализ начинают с построения графика зависимости, на его основе подбирают подходящее математическое уравнение, а затем находят параметры этого уравнения путем решения системы нормальных уравнений. Регрессионный анализ используется для изучения связей между зависимой переменной и одной или несколькими независимыми переменными, определения тесноты связи и математической зависимости между ними, предсказания значения зависимой переменной. Простейшей системой корреляционной связи является линейная связь между двумя признаками, или парная линейная корреляция. Уравнение парной линейной корреляционной связи называется уравнением парной регрессии:


a – свободный член уравнения (параметр уравнения не имеющий экономического смысла);
b – коэффициент регрессии, который выражает количественную зависимость между факторами и показывает среднее изменение результативного признака при изменении факторного на единицу.
Построение корреляционно-регрессионных моделей, какими бы сложными они не были, само по себе не вскрывает полностью всех причинно-следственных связей. Основой их адекватности является предварительный качественный анализ, основанный на учёте специфики и особенностей исследуемых социально-экономических явлений и процессов.
Регрессионный анализ — статистический метод установления зависимости между независимыми и зависимыми переменными. Регрессионный анализ на основе построенного уравнения регрессии определяет вклад каждой независимой переменной в изменение изучаемой (прогнозируемой) зависимой переменной величины. В маркетинге часто используется для прогнозирования спроса. Используется для:
· Определение факторов, влияющих на зависимую переменную (например, что в наибольшей степени влияет на капитал бренда).
· Выявление важных и неважных факторов, анализ заявленной и реальной важности.
· Построение регрессионных уравнений и моделей.
Принцип работы: На входе анализа – одна зависимая переменная и несколько независимых переменных, которые могут влиять на зависимую. Все переменные должны быть измерены по интервальным или дихотомическим шкалам. В случае, если в анализ необходимо включить порядковые переменные (например, степень согласия с рядом высказываний, измеренную по 5-балльной шкале), их необходимо предварительно оцифровать (с помощью статистического метода перекодировать в интервальные). Алгоритм простой линейной регрессии выявляет степени влияния независимых переменных на зависимую и выдаёт регрессионное уравнение вида Y = а0 + b1X1 + b2X2…+…bnXn, где Y – зависимая переменная, а0 – константа, среднее значение Y, если каждая независимая переменная равна 0, Xn – независимые переменные, bn – коэффициенты влияния независимых.
Итог: Коэффициенты влияния показывают, какие из независимых переменных влияют на зависимую положительно, а какие отрицательно, а также какова степень этого влияния. В простой линейной регрессии коэффициент, больший 0, свидетельствует о положительном влиянии данной независимой переменной на зависимую, а коэффициент, меньший 0 – об отрицательной.
С помощью регрессионного уравнения можно моделировать разные комбинации независимых переменных и предсказывать, какое значение примет в этих случаях зависимая переменная.
Выявление факторов, способных наиболее сильно влиять на целевые маркетинговые показатели. В итоге мы получаем возможность концентрировать усилия на развитии тех параметров, которые способны улучшить ситуацию, и устранении тех, которые ухудшают целевой показатель.
Дискриминантный анализ.
Дискриминантный анализ используется для принятия решения о том, какие переменные различают (дискриминируют) две или более возникающие совокупности (группы).
Дискриминантный анализ относится к группе методов анализа зависимости и внешний вид получаемой дискриминантной функции не отличается от уравнения регрессии: D = b0 + b1x1+ b2x2 +..+ bkxk. В качестве зависимой переменной выступает номинальная переменная, идентифицирующая принадлежность объектов к одной из нескольких групп. Независимые переменные ( x1, x2 .. xk ) количественные и качественные.
Основной задачей дискриминантного анализа является исследование групповых различий — различие (дискриминация) объектов по определенным признакам.
Дискриминантный анализ позволяет выяснить, действительно ли группы различаются между собой, и если да, то каким образом (какие переменные вносят наибольший вклад в имеющиеся различия).
При сравнении двух групп (бинарная зависимая переменная) формируется одна дискриминантная функция. Если данный метод применяется к анализу трех или более групп (множественный дискриминантный анализ), то могут формироваться несколько дискриминантных функций.
Важной проблемой дискриминантного анализа является определение дискриминантных переменных (переменных, входящих в дискриминантную функцию). Возможны два подхода. Первый предполагает одновременное введение всех переменных, в этом случае учитывается каждая независимая переменная, при этом ее дискриминирующая сила не принимается во внимание. Альтернативой является пошаговый (stepwise) дискриминантный анализ, при котором переменные вводятся последовательно, исходя из их способности различить (дискриминировать) группы. При пошаговом анализе «с включением» на каждом шаге просматриваются все переменные, и находится та из них, которая вносит наибольший вклад в различие между совокупностями. Эта переменная должна быть включена в модель на данном шаге, и происходит переход к следующему шагу.
При пошаговом анализе «с исключением» движутся в обратном направлении, в этом случае все переменные сначала будут включены в модель, а затем на каждом шаге будут устраняться переменные, вносящие малый вклад в различение. Тогда в качестве результатауспешного анализа можно сохранить только «важные» переменные в модели, т.е. те переменные, чей вклад в дискриминацию больше остальных. Пошаговый дискриминантный анализ основан на использовании уровня значимости F-статистики.
Проверка качества дискриминации (различия) основана на сравнении средних дискриминантной функции для исследуемых групп. Эти средние играют настолько важную роль в дискриминантном анализе, что получили свое название – центроиды (centroids). Центроидов столько, сколько групп, т.е. один центроид для каждой группы
Кроме этого, значения дискриминантной функции также имеют свое название – дискриминантные показатели (discriminant scores).
Факторный анализ.
В современной статистике под факторным анализом понимают совокупность методов, которые на основе реально существующих связей признаков, объектов или явлений позволяют выявлять латентные (скрытые и не доступные для непосредственного измерения) обобщающие характеристики организованной структуры и механизма развития изучаемых явлений или процессов.
Набор методов факторного анализа в настоящее время достаточно велик, насчитывает десятки различных подходов и приемов обработки данных. Чтобы в исследованиях ориентироваться на правильный выбор методов, необходимо представлять их особенности. Разделим все методы факторного анализа на несколько классификационных групп:
— Метод главных компонент. Строго говоря, его не относят к факторному анализу, хотя он имеет с ним много общего. Специфическим является, во-первых, то, что в ходе вычислительных процедур одновременно получают все главные компоненты и их число первоначально равно числу элементарных признаков. Во-вторых, постулируется возможность полного разложения дисперсии элементарных признаков, другими словами, ее полное объяснение через латентные факторы (обобщенные признаки).
— Методы факторного анализа. Дисперсия элементарных признаков здесь объясняется не в полном объеме, признается, что часть дисперсии остается нераспознанной как характерность. Факторы обычно выделяются последовательно: первый, объясняющий наибольшую долю вариации элементарных признаков, затем второй, объясняющий меньшую, вторую после первого латентного фактора часть дисперсии, третий и т.д. Процесс выделения факторов может быть прерван на любом шаге, если принято решение о достаточности доли объясненной дисперсии элементарных признаков или с учетом интерпретируемости латентных факторов.
Методы факторного анализа целесообразно разделить дополнительно на два класса: упрощенные и современные аппроксимирующие методы.
Простые методы факторного анализа в основном связаны с начальными теоретическими разработками. Они имеют ограниченные возможности в выделении латентных факторов и аппроксимации факторных решений. К ним относятся:
— однофакторная модель. Она позволяет выделить только один генеральный латентный и один характерный факторы. Для возможно существующих других латентных факторов делается предположение об их незначимости;
— бифакторная модель. Допускает влияние на вариацию элементарных признаков не одного, а нескольких латентных факторов (обычно двух) и одного характерного фактора;
— центроидный метод. В нем корреляции между переменными рассматриваются как пучок векторов, а латентный фактор геометрически представляется как уравновешивающий вектор, проходящий через центр этого пучка. : Метод позволяет выделять несколько латентных и характерные факторы, впервые появляется возможность соотносить факторное решение с исходными данными, т.е. в простейшем виде решать задачу аппроксимации.
Современные аппроксимирующие методы часто предполагают, что первое, приближенное решение уже найдено каким либо из способов, последующими шагами это решение оптимизируется. Методы отличаются сложностью вычислений. К этим методам относятся:
— групповой метод. Решение базируется на предварительно отобранных каким-либо образом группах элементарных признаков;
— метод главных факторов. Наиболее близок методу главных компонент, отличие заключается в предположении о существовании характерностей;
— метод максимального правдоподобия, минимальных остатков, а-факторного анализа канонического факторного анализа, все оптимизирующие.
Эти методы позволяют последовательно улучшить предварительно найденные решения на основе использования статистических приемов оценивания случайной величины или статистических критериев, предполагают большой объем трудоемких вычислений.
Кластерный анализ
Кластерный анализ – это совокупность методов, позволяющих классифицировать многомерные наблюдения, каждое из которых описывается набором исходных переменных X1, X2, . Хт. Целью кластерного анализа является образование групп схожих между собой объектов, которые принято называть кластерами (cluster).
В отличие от комбинационных группировок кластерный анализ приводит к разбиению на группы с учетом всех группировочных признаков одновременно. Например, если каждый наблюдаемый объект характеризуется двумя признаками Х1 и Х2, то при выполнении комбинационной группировки вся совокупность объектов будет разбита на группы по Х1, а затем внутри каждой выделенной группы будут образованы подгруппы по Х2. Определить принадлежность каждого объекта к той или иной группе можно, последовательно сравнивая его значения Х1 и Х2 с границами выделенных групп. Образование группы в этом случае всегда связано с указанием ее границ по каждому группировочному признаку отдельно.
В кластерном анализе используется иной принцип образования групп. Все группировочные признаки одновременно участвуют в группировке, т.е. они учитываются все сразу при отнесении наблюдения в ту или иную группу. При этом, как правило, не указаны четкие границы каждой группы, а также неизвестно заранее, сколько же групп целесообразно выделить в исследуемой совокупности. Таким образом, методы кластерного анализа помогают построить научно обоснованные классификации путем выявления внутренних связей между единицами наблюдаемой совокупности.
Методы кластерного анализа позволяют решать следующие задачи:
· проведение классификации объектов с учетом признаков, отражающих сущность, природу объектов. Решение такой задачи, как правило, приводит к углублению знаний о совокупности классифицируемых объектов;
· проверку выдвигаемых предположений о наличии некоторой структуры в изучаемой совокупности объектов, т.е. поиск существующей структуры;
· построение новых классификаций для слабоизученных явлений, когда необходимо установить наличие связей внутри совокупности и попытаться привнести в нее структуру.
Методы кластерного анализа можно разделить на две большие группы: агломеративные (объединяющие) и дивизимные (разделяющие). Агломеративные методы последовательно объединяют отдельные объекты в группы (кластеры), а дивизимные методы расчленяют группы на отдельные объекты. В свою очередь, каждый метод как объединяющего, так и разделяющего типа может быть реализован при помощи различных алгоритмов. Отдельные примеры агломеративных и дивизимных алгоритмов рассмотрены в разд. 8.2.3. В частности, наиболее подробно описан самый доступный для понимания иерархический агломеративный кластерный анализ. Следует заметить, что как агломеративные, так и дивизимные алгоритмы трудоемки и их сложно использовать для больших совокупностей. Кроме того, результаты работы таких алгоритмов (их графическое изображение) трудно поддаются визуальному анализу.
Кластерный анализ носит количественный характер, но статистические пакеты обычно не предлагают методов проверки гипотезы об адекватности получаемых классификаций.
Кластерный анализ – набор переменных, описывающих совокупность респондентов. Метод работает с интервальными (например, возраст, доход, оценка степени согласия по 10-балльной шкале и т.д.) и дихотомическими переменными (например, пол, наличие/отсутствие руководящих функций) переменными. Совокупность из n значений по всем n переменным определяет положение объекта в неком n-мерном пространстве. Исходя из этих координат определяются расстояния между объектами. Для расчёта расстояний чаще всего используется Евклидово расстояние, однако метод расчёта расстояний может варьироваться в зависимости от специфики данных. Метод группирует схожие (расположенные близко друг к другу) объекты, в результате чего формируется набор из нескольких кластеров. Число кластеров может определяться автоматически на основе выбранного критерия либо выбираться вручную исследователем с учётом теоретических предпосылок и понимания предмета исследования. Существует несколько процедур кластеризации, но все они базируются на использовании мер или критериев близости. Наиболее распространенным критерием близости является среднеквадратическая разность. Евклидово расстояние — расстояние между объектами d (Xi; Xj) = [å (Xik — Xjk)2 ] 2 Суть в том, что последовательно объединяются объекты сначала более близкие, а затем все более отдаленные друг от друга. Работа алгоритма заканчивается, когда все объекты будут объединены в один класс. Результатом обычно является графическое изображение, иллюстрирующее вид иерархического дерева (дендрограмма). Описанный алгоритм не имеет четких правил остановки на каком-то этапе кластеризации. Обычно исследователи принимают во внимание устойчивость групп на протяжении нескольких шагов алгоритма. В кластерном анализе не рекомендуется использовать большое количество факторов.
На выходе – набор кластеров/сегментов. Каждый сегмент описывается средними по кластеру значениями переменных. С помощью этих данных можно выделить характерные особенности сегментов, их отличительные черты. При хорошем кластерном решении дисперсия значений переменных внутри кластера должна быть минимальной (т.е. респонденты внутри кластера однородны), а дисперсия между кластерами максимальна (т.е. респонденты из одного кластера не похожи на респондентов из другого).
Хорошее кластерное решение даёт яркие и чётко различающиеся сегменты. На основе данных кластерного анализа можно выбирать разные стратегии работы с каждым из сегментов. Тем не менее, т.к. метод основан на расстояниях между объектами, он не работает с типами переменных, которые не дают возможности рассчитать эти расстояния – категориальными и порядковыми. В случае с такими типами переменных для проведения сегментации рекомендуется использовать CHAID- анализ.
1. Галицкий, Е. Б. Маркетинговые исследования : учебник для магистров / Е. Б. Галицкий, Е. Г. Галицкая. — М. : Издательство Юрайт, 2012. — 540 с. — Серия : Магистр.
2. Тюрин Д. В. Маркетинговые исследования: учебник для бакалавров/ Д. В. Тюрин — М.: Издательство Юрайт, 2013. — 342 с. — Серия: Бакалавр. Углубленный курс.
3. Крюков, А.Ф. Управление маркетингом [Текст]: учебное пособие / А.Ф. Крюков. — М.: КНОРУС. — 2006. – 470 с.
📸 Видео
Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Парная регрессия: линейная зависимостьСкачать

Множественная регрессияСкачать

Эконометрика Линейная регрессия и корреляцияСкачать

РЕГРЕССИОННЫЙ АНАЛИЗ STATISTICA #12Скачать

Факторный анализ Метод абсолютных разницСкачать

Практика Многофакторная регрессияСкачать

Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

Линейная регрессияСкачать

Уравнение регрессииСкачать

Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Множественная регрессия в ExcelСкачать