Уравнения реакций до температуры 500 600 градусов

Видео:Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Уравнения реакций до температуры 500 600 градусов

Большинство химических реакций протекают одновременно в двух направлениях: в сторону образования продуктов реакции (прямая реакция) и в сторону разложения последних (обратная реакция). Вследствие химической обратимости реакции не доходят до конца. Скорость прямой реакции уменьшается, а скорость обратной, напротив, возрастает. Когда эти скорости выравниваются наступает состояние химического равновесия.

Так как химически обратимые реакции до перехода в равновесное состояние протекают с конечными скоростями, то с точки зрения термодинамики они не обратимы. Однако можно мысленно представить, что эти реакции идут бесконечно медленно через смежные равновесные состояния. Тогда к ним можно применить общие условия термодинамического равновесия.

Для гомогенных обратимых реакций экспериментально Гульбергом и Ваге был установлен закон действующих масс. При постоянной температуре отношение произведения равновесных концентраций (или парциальных давлений) продуктов реакции к произведению равновесных концентраций (или парциальных равновесий) исходных веществ есть величина постоянная.

Этот экспериментально установленный закон может быть получен методом термодинамических потенциалов. Рассмотрим реакцию в газовой фазе:

аА(г) + b В ↔ сС + dD

Когда система достигает термодинамического равновесия, то термодинамический потенциал при фиксированных естественных переменных достигает минимума. Равновесие, таким образом, можно охарактеризовать выражением химических потенциалов, когда потенциалы продуктов реакции сравняются с потенциалами исходных веществ:

с μ ( с ) + d μ (D) – a μ (a) — b μ (b) = 0 (6 – 1)

Если естественными переменными являются p и T , то = , а = V

Отсюда для систем, подчиняющихся закону идеальных газов, можно получить выражения для μ i

μ i = μ i ° + RTlnCi (6 – 2)

где μ i ° — стандартный химический потенциал.

Подставляется (6 – 2) в (6 – 1) и перенося постоянные величины в левую часть, получаем

сμ C ° + d μ D ° — a μ A ° — b μ B ° = — RTln (6 – 3)

Поскольку в левой части выражение не зависит от концентраций, то выражение под логарифмом является постоянной величиной при постоянной температуре:

Для идеального газа парциальные давления пропорциональны концентрациям, поэтому константа равновесия может быть всегда выражена через равновесные парциальные давления:

Аналогично может быть записано выражение через мольные доли:

Для идеальных газов эти константы связаны между собой соотношением:

где

Следует обратить внимание, что в полученных соотношениях только KN зависит от общего давления. Она позволяет нам оценивать сдвиг равновесия в газовых реакциях при изменении общего давления. Следует иметь в виду, что давление в этих выражениях складывается из парциальных давлений компонентов системы и не учитывает влияние инертных газов, если они присутствуют в реакционной смеси. Естественно инертный газ «разбавляет» компоненты реакционной смеси и поэтому влияет на KN .

Из уравнения (6 – 3) вытекает связь константы равновесия с ∆ rG °:

(6 – 4)

Это уравнение было впервые получено Вант – Гофором методом циклов и получило название уравнения изотермической химической реакции. Очевидно, в этом уравнении ∆ rGT ° относится к этой температуре, при которой определена Кр. Уравнение изотермической химической реакции позволяет определить константу равновесия при заданных условиях не прибегая к исследованию равновесия. Величина ∆ rGT ° может быть рассчитана на основе термических констант для индивидуальных веществ.

Если заданы концентрации (парциальные давления) отличные от равновесных, то можно записать более общий вид уравнения изотермической химической реакции:

Это выражение позволяет определить направление самопроизвольного процесса.

Уравнение изотермы химической реакции позволяет получить выражение для температурной зависимости константы равновесия.

Запишем уравнение Гиббса – Гельмгольца:

Подставим выражение для из (6 – 4)

(6 — 5)

Дифференцируем уравнение (6 – 5)

(6 — 5´)

Из уравнения (6 — 5´) получаем уравнение изобары химической реакции:

(6 – 6)

Если проинтегрировать уравнение (6 – 6) в предположении, что ∆ rHT ° не зависит от температуры, то получим уравнение:

где С – константа интегрирования.

Уравнение (6 – 7) хорошо выполняется в узких интервалах температур и позволяет определить ∆ rGT °.

Для широких интервалов температур ln K р представляют в виде степенных рядов или других аналитических формах:

Такие выражения позволяют рассчитать все термодинамические функции для процессов, для которых данные зависимости получены.

Выражения для термодинамических потенциалов, полученные для идеального газа. Для реальных газов, а особенно для газовых растворов возникают затруднения. Это связано с тем, что расчет концентраций и давлений должен быть проведен исходя из уравнения состояния. Однако для реальных систем единое достаточно простое уравнение состояния получить не удалось.

В связи с этим в термодинамике реальных систем применяется эмпирический метод, предложенный Льюисом. Льюис предложил в уравнениях термодинамики, полученных для идеальных систем заменить давления p на величину летучести f , а концентрации С на активности a .

При такой замене выражения для констант равновесия не меняются по форме. Но этот прием позволяет связать экспериментально найденные свойства реального газа с термодинамическими параметрами.

Летучести и активности – это экспериментальные величины, которые находятся из условия, что для раствора при бесконечном разбавлении или газа при давлении стремящимся к 0 активность приближается к аналитической концентрации, а летучесть к реальному давлению идеального газа. Исходя из этой посылки рассчитываются активности и летучести.

При 1273 К и общем равновесии 30 атм. В равновесной системе

содержится 17% (по общему) . Сколько процентов будет содержаться в газе при общем давлении 20 атм.? При каком давлении в газе будет содержаться 25% ? (Газ считать идеальным).

В соответствии с законом Авогадро, объёмный процент равен мольному проценту. Следовательно, при 30 атм. будет равен:

Отсюда находим

В отличие от , для идеальных газов не зависит от давления. На основании этого находим при 20 атм.

= 0,125 или 12,5%

Для 25%

Следовательно,

При 2000°С и общем давлении 1 атм. 2% воды диссоцииовано на водород и кислород. Рассчитайте константу равновесия реакции при этих условиях.

Видео:Влияние температуры на скорость химических реакций. 10 класс.Скачать

Примеры решения типовых задач

Глава I. Химическая термодинамика

1. Определить тепловой эффект химической реакции в стандартных условиях при 500 К: СН₃ОН + 3/2 О_2(г) = СO_2(г) + 2Н₂O

Из справочника [8] выпишем необходимые для расчёта термодинамические величины

Для расчёта теплового эффекта и изменения теплоёмкости применим следствие из закона Гесса, при этом учитываем, что для простых веществ стандартная теплота образования равна нулю.

ΔH 0 _{298, х.р.} = ΔН 0 _{298, f ( )} + 2ΔН 0 _{298, f ( )} – ΔН 0 _{298, f ( )} =

= (– 393,51) + 2(–241,84) – (–201,2) = – 675,99 кДж.

Знак минус перед тепловым эффектом означает, что теплота выделяется в результате реакции.

ΔС 0 _{р, 298} = (С_{р( )} + 2С_{р( )}) – (С_{р( )} – С_{р( )}) =

= ( 37,13 + 2·33,56 ) – ( 43,9 + 3/2·29,36) = 16,31 Дж/К

Тепловой эффект при 500 К находим по уравнению Кирхгофа (второе приближение), при условии, что средняя изобарная теплоемкость постоянна

ΔН 0 _{500 х.р.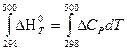} = = ΔН 0 ₂₉₈ + = ΔН 0 ₂₉₈ + ΔC_p (500 – 298) =

= – 675,99·10 3 + 16,31(500 – 298) = 672,70·10 3 Дж = 672,7 кДж

2. Рассчитать (по теплотам сгорания) стандартную теплоту образования глицерина С₃Н₈О_{3 (ж)}.

Из определения теплоты образования следует, что H_{298, f ( 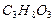)} – это тепловой эффект реакции:

используя следствие из закона Гесса, можно записать:

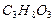
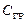
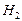
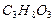
Δ H_{298, f ( )} = 3ΔH_{сгор ( )} + 4ΔН _{сгор ( )} – ΔН _{сгор ( )}

Теплоты сгорания простых веществ при стандартных условиях численно равны стандартным теплотам образования продуктов сгорания, т.е. для реакций

из справочника [8] определяем:

ΔН_{298, сгор ( 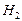)} = ΔН_{298, f ( )} = – 285,83 кДж/моль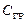

ΔН_{298, сгор ( 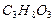)} = ΔH_{298, f ( )} = – 393,51 кДж/моль

ΔН_{298, сгор ( )} = – 1661,05 кДж/моль

ΔН_{f, 298 ( 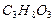)} = [3(– 393,51)+4(– 285,83)] – [– 1661,05] = – 602,8 кДж/моль

По справочным данным эта величина равна – 668,6 Кдж/моль.

3. Дайте заключение о возможности самопроизвольного протекания химической реакции при Т = 298 К

молочная кислота пировиноградная к-та

Рассчитаем по следствию из закона Гесса:

1. Изменение энтальпии: ΔН 0 _{298, р} = (– 586 + 0) – (– 673) = 87 (кДж)

2. Изменение энтропии: ΔS 0 _{298, p} = (179 + 130) – 192 =117 (Дж/К)
3. Изменение энергии Гиббса по уравнению Гиббса-Гельмгольца (первое приближение):

ΔG 0 ₂₉₈ = ΔH 0 ₂₉₈ – TΔS = 87·10 3 – 298·117 = 52134 (Дж)

реакция самопроизвольно протекать не может, т.к. ΔG 0 ₂₉₈ > 0

4. При 1000 К и 1,013·10 5 Па из исходной смеси, содержащей 1 моль SО₂ и 0,6 моль О₂ при достижении равновесия образовалось 0,22 моль SО₃. Определить Кр для реакции

2SО₂ + О₂ 2SО₃

На образование 0,22 моль SО₃, согласно уравнению реакции израсходовано 0,22 моль SО₂ и 0,11 моль кислорода. Запишем число молей

P( ) = n( )·P_общ = (0,78/1,49)·1,013·10 5 = 5,31·10 4 Па

Р( ) = n( )·P_общ = (0,49/1,49)·1,013·10 5 = 3,22·10 4 Па

P( ) = n( )·P_общ= (0,22/1,49)·1,013·10 5 = 1,5·10 4 Па

5. Для реакции: СО + Cl₂ COCl₂ при 600 °С константа равновесия равна 6,386. В каком направлении будет протекать реакция, если в 1 л реакционной смеси находится

а) 1моль СО; 1 моль Cl₂; 4 моль COCl₂

б) 1моль СО; 1 моль Сl; 8 моль COCl₂

в) 1моль СО; 1,565 моль Cl₂; 10 моль COCl₂

Воспользуемся уравнением изотермы химической реакции.

а) ΔG = – RTln·6,386 + RT·ln 4

He производя вычислений, а лишь сравнивая величины, стоящие за знаком логарифма, можно сделать вывод, что G 0. Это значит, что при смешивании реагирующих веществ в указанных соотношениях реакция пойдёт в сторону образования СО и Cl₂;

в) ΔG = – RTln 6,386 + RTln 6,386

Сравнив оба слагаемых, можно сделать вывод, что ΔG = 0. В этом случае система находится в состоянии химического равновесия.

6. Рассчитать значение константы равновесия для реакции при стандартных условиях и 1000 К, если изменение энергии Гиббса равно – 100,79 кДж.

Воспользуемся уравнением изотермы при стандартных условиях.

lgKp = (– ΔG 0 _T) / (2,3·RT) = (–100,79) / (2,3·8,31·1000) = 5,27

Видео:Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Реакции разложения

При выполнении различных заданий ЕГЭ по химии (например, задачи 34 или задания 32 «мысленный эксперимент») могут пригодиться знания о том, какие вещества при нагревании разлагаются и как они разлагаются.

Рассмотрим термическую устойчивость основных классов неорганических веществ. Я не указываю в условиях температуру протекания процессов, так как в ЕГЭ по химии такая информация, как правило, не встречается. Если возможны различные варианты разложения веществ, я привожу наиболее вероятные, на мой взгляд, реакции.

Видео:Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Разложение оксидов

При нагревании разлагаются оксиды тяжелых металлов:

2HgO = 2Hg + O₂

Видео:Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Разложение гидроксидов

Как правило, при нагревании разлагаются нерастворимые гидроксиды. Исключением является гидроксид лития, он растворим, но при нагревании в твердом виде разлагается на оксид и воду:

2LiOH = Li₂O + H₂O

Гидроксиды других щелочных металлов при нагревании не разлагаются.

Гидроксиды серебра (I) и меди (I) неустойчивы:

2AgOH = Ag₂O + H₂O

2CuOH = Cu₂O + H₂O

Гидроксиды большинства металлов при нагревании разлагаются на оксид и воду.

В инертной атмосфере (в отсутствии кислорода воздуха) гидроксиды хрома (III) марганца (II) и железа (II) распадаются на оксид и воду:

Большинство остальных нерастворимых гидроксидов металлов также при нагревании разлагаются:

Видео:Решение задач на термохимические уравнения. 8 класс.Скачать

Разложение кислот

При нагревании разлагаются нерастворимые кислоты.

Например , кремниевая кислота:

Некоторые кислоты неустойчивы и подвергаются разложению в момент образования. Большая часть молекул сернистой кислоты и угольной кислоты распадаются на оксид и воду в момент образования:

В ЕГЭ по химии лучше эти кислоты записывать в виде оксида и воды.

Например , при действии водного раствора углекислого газа на карбонат калия в качестве реагента мы указываем не угольную кислоту, а оксид углерода (IV) и воду, но подразумеваем угольную кислоту при этом:

Азотистая кислота на холоде или при комнатной температуре частично распадается уже в водном растворе, реакция протекает обратимо:

При нагревании выше 100 о С продукты распада несколько отличаются:

Азотная кислота под действием света или при нагревании частично обратимо разлагается:

Видео:Как температура влияет на скорость химической реакции? Уравнение АррениусаСкачать

Разложение солей

Видео:№ 501-600 - Физика 10-11 класс РымкевичСкачать

Разложение хлоридов

Хлориды щелочных, щелочноземельных металлов, магния, цинка, алюминия и хрома при нагревании не разлагаются.

Хлорид серебра (I) разлагается под действием света:

2AgCl → Ag + Cl₂

Хлорид аммония при нагревании выше 340 о С разлагается:

Видео:Влияние концентрации на скорость химических реакций. 10 класс.Скачать

Разложение нитратов

Нитраты щелочных металлов при нагревании разлагаются до нитрита металла и кислорода.

Например , разложение нитрата калия:

Видеоопыт разложения нитрата калия можно посмотреть здесь.

Нитраты магния, стронция, кальция и бария разлагаются до нитрита и кислорода при нагревании до 500 о С:

При более сильном нагревании (выше 500 о С) нитраты магния, стронция, кальция и бария разлагаются до оксида металла, оксида азота (IV) и кислорода:

Нитраты металлов, расположенных в ряду напряжений после магния и до меди (включительно) + нитрат лития разлагаются при нагревании до оксида металла, диоксида азота и кислорода:

Нитраты серебра и ртути разлагаются при нагревании до металла, диоксида азота и кислорода:

Нитрат аммония разлагается при небольшом нагревании до 270 о С оксида азота (I) и воды:

При более высокой температуре образуются азот и кислород:

Видео:ДВИ по химии. Термохимия. Уравнение Аррениуса, закон Гесса, задачи на теплоемкостьСкачать

Разложение карбонатов и гидрокарбонатов

Карбонаты натрия и калия плавятся при нагревании.

Карбонаты лития, щелочноземельных металлов и магния разлагаются на оксид металла и углекислый газ:

Карбонат аммония разлагается при 30 о С на гидрокарбонат аммония и аммиак:

Гидрокарбонат аммония при дальнейшем нагревании разлагается на аммиак, углекислый газ и воду:

Гидрокарбонаты натрия и калия при нагревании разлагаются на карбонаты, углекислый газ и воду:

Гидрокарбонат кальция при нагревании до 100 о С разлагается на карбонат, углекислый газ и воду:

При нагревании до 1200 о С образуются оксиды:

Видео:Химические уравнения - Как составлять уравнения реакций // Составление Уравнений Химических РеакцийСкачать

Разложение сульфатов

Сульфаты щелочных металлов при нагревании не разлагаются.

Сульфаты алюминия, щелочноземельных металлов, меди, железа и магния разлагаются до оксида металла, диоксида серы и кислорода:

Сульфаты серебра и ртути разлагаются до металла, диоксида серы и кислорода:

Видео:Урок 112 (осн). Уравнение теплового балансаСкачать

Разложение фосфатов, гидрофосфатов и дигидрофосфатов

Эти реакции, скорее всего, в ЕГЭ по химии не встретятся! Гидрофосфаты щелочных и щелочноземельных металлов разлагаются до пирофосфатов:

Ортофосфаты при нагревании не разлагаются (кроме фосфата аммония).

Видео:Абсолютная температура | Физика 10 класс #31 | ИнфоурокСкачать

Разложение сульфитов

Сульфиты щелочных металлов разлагаются до сульфидов и сульфатов:

Видео:Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать

Разложение солей аммония

Некоторые соли аммония, не содержащие анионы кислот-сильных окислителей, обратимо разлагаются при нагревании без изменения степени окисления. Это хлорид, бромид, йодид, дигидрофосфат аммония:

Cоли аммония, образованные кислотами-окислителями, при нагревании также разлагаются. При этом протекает окислительно-восстановительная реакция. Это дихромат аммония, нитрат и нитрит аммония:

Видеоопыт разложения нитрита аммония можно посмотреть здесь.

Видео:8 класс. Массовая доля растворенного вещества. Решение задач.Скачать

Разложение перманганата калия

Видео:Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Химия ПростоСкачать

Разложение хлората и перхлората калия

Хлорат калия при нагревании разлагается до перхлората и хлорида:

4KClO₃ → 3KClO₄ + KCl

При нагревании в присутствии катализатора (оксид марганца (IV)) образуется хлорид калия и кислород:

2KClO₃ → 2KCl + 3O₂

Перхлорат калия при нагревании разлагается до хлорида и кислорода:

📹 Видео

Количество теплоты, удельная теплоемкость вещества. Практическая часть - решение задачи. 8 класс.Скачать

Как решать задачи по химии? Расчет по уравнениям химических реакций | TutorOnlineСкачать

Химия | Тепловой эффект химической реакции (энтальпия)Скачать

Обратимость и необратимость химических реакций. Химическое равновесие. 1 часть. 9 класс.Скачать