Уравнения разомкнутой и замкнутой сау

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ

АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ.

СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Под управлением технологическим процессом понимается совокупность операций, необходимых для осуществления таких целей, как пуск и остановка технологического процесса, поддержание какого-либо параметра процесса на заданном уровне, изменение параметра по заданной программе и т.п.

Установку, машину, агрегат, в котором протекает исследуемый технологический процесс, называют объектом управления.Управление может быть ручным или автоматическим. В первом случае операции управления осуществляет человек, а во втором – управляющее устройство. Сочетание объекта управления и управляющего устройства образует систему автоматического управления (САУ).

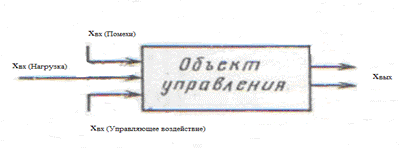
Рис.11.1. К понятию системы автоматического управления

На работу системы автоматического управления влияют различные воздействия. Будем называть их входными воздействиями, входными величинами или просто входами (x_вх) (рис.11.1).

Параметры процесса, которые в той или иной степени характеризуют его качество и изменяются под действием входных величин, будем называть выходными величинами или просто выходами(x_вых). Входные воздействия, которые нарушают заданный закон изменения выходных величин, будем называть возмущающими воздействиями или просто возмущениями. Возмущения можно подразделить на два вида: нагрузку (Н) и помехи (П). Изменение нагрузки обычно обусловлено технологическим процессом, а помехи вызываются изменениями внешних условий (например, температуры окружающей среды) или свойств отдельных элементов системы.

Воздействие управляющего устройства на объект управления называется управляющим воздействием (У).Оно также относится к входным воздействиям.

ОБРАТНЫЕ СВЯЗИ.

При построении системы автоматического управления широко применяют обратные связи.

Обратную связь называют внешней, если она соединяет выход системы с ее входом, и внутренней или местной, если она соединяет выход одного или группы элементов системы с их входом.

Если подача выходной величины элемента системы на его вход усиливает действие входной величины на выходную, то такая обратная связь называется положительной.

Обратная связь называется отрицательной, если подача выходной величины элемента системы на его вход ослабляет действие входной величины на выходную.

По характеру передачи воздействий обратные связи делятся на жесткие и гибкие. Жесткая связь действует как в установившемся, так и в переходном режиме, гибкая действует только в переходном режиме, а в установившемся режиме ее действие прекращается.

РАЗОМКНУТЫЕ И ЗАМКНУТЫЕ САУ.

Системы автоматического управления делятся на разомкнутые и замкнутые.

Разомкнутыми называются такие системы автоматического управления, в которых отсутствует внешняя обратная связь и, следовательно, отсутствует контроль результата управления.

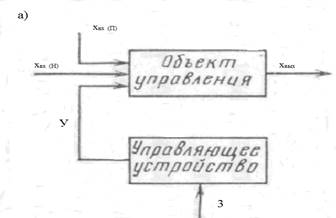
В разомкнутой САУ с жесткой программой(рис.11.2,а) на управляющее устройство подается жесткое задание З. Управляющее устройство оказывает воздействие У на объект управления в соответствии с этим заданием. Под действием некоторого возмущенияx_вх (например, изменение нагрузки) могут возникнуть отклонения выходной величиныx_вых объекта от задания. Однако эти отклонения в разомкнутой САУ с жесткой программой не контролируются и не влияют на работу управляющего устройства.

Рис.11.2. Разомкнутые системы автоматического управления (САУ)

К таким системам относятся, например, системы автоматического пуска и остановки насосов, вентиляторов, компрессоров и т.п.

Замкнутыминазывают системы автоматического управления, в которых имеется обратная связь, обеспечивающая контроль выходной величины (рис.11.3,а).

При этом управляющее устройство формирует управляющее воздействие У в зависимости от отклонения входной величины x_вых от задания З.

Видео:proТАУ: 1. Передаточная функцияСкачать

Введение в теорию автоматического управления. Основные понятия теории управления техническим системами

Публикую первую главу лекций по теории автоматического управления, после которых ваша жизнь уже никогда не будет прежней.

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика привествуется.

Видео:7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

1. Основные понятия теории управления техническими системами

Видео:Теория автоматического управления. Лекция 11. Критерий НайквистaСкачать

1.1. Цели, принципы управления, виды систем управления, основные определения, примеры

Развитие и совершенствование промышленного производства (энергетики, транспорта, машиностроения, космической техники и т.д.) требует непрерывного увеличения производительности машин и агрегатов, повышения качества продукции, снижения себестоимости и, особенно в атомной энергетике, резкого повышения безопасности (ядерной, радиационной и т.д.) эксплуатации АЭС и ядерных установок.

Реализация поставленных целей невозможна без внедрения современных систем управления, включая как автоматизированные (с участием человека-оператора), так и автоматические (без участия человека-оператора) системы управления (СУ).

Определение: Управление – это такая организация того или иного технологического процесса, которая обеспечивает достижение поставленной цели.

Теория управления является разделом современной науки и техники. Она базируется (основывается) как на фундаментальных (общенаучных) дисциплинах (например, математика, физика, химия и т.д.), так и на прикладных дисциплинах (электроника, микропроцессорная техника, программирование и т.д.).

Любой процесс управления (автоматического) состоит из следующих основных этапов (элементов):

• получение информации о задаче управления;
• получение информации о результате управления;
• анализ получаемой информации;
• выполнение решения (воздействие на объект управления).

Для реализации Процесса Управления система управления (СУ) должна иметь:

• источники информации о задаче управления;
• источники информации о результатах управления (различные датчики, измерительные устройства, детекторы и т.д.);
• устройства для анализа получаемой информации и выработки решения;
• исполнительные устройства, воздействующие на Объект Управления, содержащие: регулятор, двигатели, усилительно-преобразующие устройства и т.д.

Определение: Если система управления (СУ) содержит все перечисленные выше части, то она является замкнутой.

Определение: Управление техническим объектом с использованием информации о результатах управления называется принципом обратной связи.

Схематично такая система управления может быть представлена в виде:

Рис. 1.1.1 — Структура системы управления (СУ)

Если система управления (СУ) имеет структурную схему, вид которой соответствует рис. 1.1.1, и функционирует (работает) без участия человека (оператора), то она называется системой автоматического управления (САУ).

Если СУ функционирует с участием человека (оператора), то она называется автоматизированной СУ.

Если Управление обеспечивает заданный закон изменения объекта во времени независимо от результатов управления, то такое управление совершается по разомкнутому циклу, а само управление называется программным управлением.

К системам, работающим по разомкнутому циклу, относятся промышленные автоматы (конвейерные линии, роторные линии и т.д.), станки с числовым программным управлением (ЧПУ): см. пример на рис. 1.1.2.

Задающее устройство может быть, например, и “копиром”.

Поскольку в данном примере нет датчиков (измерителей), контролирующих изготавливаемую деталь, то если, например, резец был установлен неправильно или сломался, то поставленная цель (изготовление детали) не может быть достигнута (реализована). Обычно в системах подобного типа необходим выходной контроль, который будет только фиксировать отклонение размеров и формы детали от желаемой.

Автоматические системы управления подразделяются на 3 типа:

• системы автоматического управления (САУ);
• системы автоматического регулирования (САР);
• следящие системы (СС).

САР и СС являются подмножествами САУ ==> .

Определение: Автоматическая система управления, обеспечивающая постоянство какой-либо физической величины (группы величин) в объекте управления называется системой автоматического регулирования (САР).

Системы автоматического регулирования (САР) — наиболее распространенный тип систем автоматического управления.

Первый в мире автоматический регулятор (18-е столетие) – регулятор Уатта. Данная схема (см. рис. 1.1.3) реализована Уаттом в Англии для поддержания постоянной скорости вращения колеса паровой машины и, соответственно, для поддержания постоянства скорости вращения (движения) шкива (ремня) трансмиссии.

В данной схеме чувствительными элементами (измерительными датчиками) являются “грузы” (сферы). «Грузы» (сферы) также “заставляют” перемещаться коромысло и затем задвижку. Поэтому данную систему можно отнести к системе прямого регулирования, а регулятор — к регулятору прямого действия, так как он одновременно выполняет функции и “измерителя” и “регулятора”.

В регуляторах прямого действия дополнительного источника энергии для перемещения регулирующего органа не требуется.

В системах непрямого регулирования необходимо присутствие (наличие) усилителя (например, мощности), дополнительного исполнительного механизма, содержащего, например, электродвигатель, серводвигатель, гидропривод и т.д.

Примером САУ (системы автоматического управления), в полном смысле этого определения, может служить система управления, обеспечивающая вывод ракеты на орбиту, где управляемой величиной может быть, например, угол между осью ракеты и нормалью к Земле ==> см. рис. 1.1.4.а и рис. 1.1.4.б

Видео:1) ТАУ (Теория автоматического управления) для чайников. Часть 1: основные понятия...Скачать

1.2. Структура систем управления: простые и многомерные системы

В теории управления техническими системами часто бывает удобно систему разделить на набор звеньев, соединенных в сетевые структуры. В простейшем случае система содержит одно звено, на вход которого подается входной воздействие (вход), на входе получается отклик системы (выход).

В теории Управления Техническими Системам используют 2 основных способа представления звеньев систем управления:

— в переменных “вход-выход”;

— в переменных состояния (более подробно см. разделы 6…7).

Представление в переменных “вход-выход” обычно используется для описания относительно простых систем, имеющих один “вход” (одно управляющее воздействие) и один “выход” (одна регулируемая величина, см. рисунок 1.2.1).

Обычно такое описание используется для технически несложных САУ (систем автоматического управления).

В последнее время широкое распространение имеет представление в переменных состояния, особенно для технически сложных систем, в том числе и для многомерных САУ. На рис. 1.2.2 приведено схематичное представление многомерной системы автоматического управления, где u₁(t)…u_m(t) — управляющие воздействия (вектор управления), y₁(t)…y_p(t) — регулируемые параметры САУ (вектор выхода).

Рассмотрим более детально структуру САУ, представленную в переменных “вход-выход” и имеющую один вход (входное или задающее, или управляющее воздействие) и один выход (выходное воздействие или управляемая (или регулируемая) переменная).

Предположим, что структурная схема такой САУ состоит из некоторого числа элементов (звеньев). Группируя звенья по функциональному принципу (что звенья делают), структурную схему САУ можно привести к следующему типовому виду:

Рис. 1.2.3 — Структурная схема системы автоматического управления

Символом ε(t) или переменной ε(t) обозначается рассогласование (ошибка) на выходе сравнивающего устройства, которое может “работать” в режиме как простых сравнительных арифметических операций (чаще всего вычитание, реже сложение), так и более сложных сравнительных операций (процедур).

Задача системы управления состоит в том (если она устойчива), чтобы “работать” на уничтожение рассогласования (ошибки) ε(t), т.е. ==> ε(t) → 0.

Следует отметить, что на систему управления действуют как внешние воздействия (управляющее, возмущающее, помехи), так и внутренние помехи. Помеха отличается от воздействия стохастичностью (случайностью) своего существования, тогда как воздействие почти всегда детерминировано.

Для обозначения управляющего (задающего воздействие) будем использовать либо x(t), либо u(t).

Видео:Теория автоматического управления. Лекция 6. Структурные схемы САУСкачать

1.3. Основные законы управления

Если вернуться к последнему рисунку (структурная схема САУ на рис. 1.2.3), то необходимо “расшифровать” роль, которую играет усилительно-преобразующее устройство (какие функции оно выполняет).

Если усилительно-преобразующее устройство (УПУ) выполняет только усиление (или ослабление) сигнала рассогласования ε(t), а именно: , где – коэффициент пропорциональности (в частном случае = Const), то такой режим управления замкнутой САУ называется режимом пропорционального управления (П-управление).

Если УПУ выполняет формирование выходного сигнала ε1(t), пропорционального ошибке ε(t) и интегралу от ε(t), т.е. , то такой режим управления называется пропорционально-интегрирующим (ПИ-управление). ==> , где b – коэффициент пропорциональности (в частном случае b = Const).

Обычно ПИ-управление используется для повышения точности управления (регулирования).

Если УПУ формирует выходной сигнал ε₁(t), пропорциональный ошибке ε(t) и ее производной, то такой режим называется пропорционально-дифференцирующим (ПД-управление): ==>

Обычно использование ПД-управления повышает быстродействие САУ

Если УПУ формирует выходной сигнал ε₁(t), пропорциональный ошибке ε(t), ее производной, и интегралу от ошибки ==> , то такой режим называетсято такой режим управления называется пропорционально-интегрально-дифференцирующим режимом управления (ПИД-управление).

ПИД-управление позволяет зачастую обеспечить “хорошую” точность управления при “хорошем” быстродействии

Видео:23) Построение Л.А.Ч.Х. и Л.Ф.Ч.Х. системы по её передаточной функцииСкачать

1.4. Классификация систем автоматического управления

1.4.1. Классификация по виду математического описания

По виду математического описания (уравнений динамики и статики) системы автоматического управления (САУ) подразделяются на линейные и нелинейные системы (САУ или САР).

Каждый “подкласс” (линейных и нелинейных) подразделяется на еще ряд “подклассов”. Например, линейные САУ (САР) имеют различия по виду математического описания.
Поскольку в этом семестре будут рассматриваться динамические свойства только линейных систем автоматического управления (регулирования), то ниже приведем классификацию по виду математического описания для линейных САУ (САР):

1) Линейные системы автоматического управления, описываемые в переменных «вход-выход» обыкновенными дифференциальными уравнениями (ОДУ) с постоянными коэффициентами:

где x(t) – входное воздействие; y(t) – выходное воздействие (регулируемая величина).

Если использовать операторную («компактную») форму записи линейного ОДУ, то уравнение (1.4.1) можно представить в следующем виде:

где, p = d/dt — оператор дифференцирования; L(p), N(p) — соответствующие линейные дифференциальные операторы, которые равны:

2) Линейные системы автоматического управления, описываемые линейными обыкновенными дифференциальными уравнениями (ОДУ) с переменными (во времени) коэффициентами:

В общем случае такие системы можно отнести и к классу нелинейных САУ (САР).

3) Линейные системы автоматического управления, описываемые линейными разностными уравнениями:

где f(…) – линейная функция аргументов; k = 1, 2, 3… — целые числа; Δt – интервал квантования (интервал дискретизации).

Уравнение (1.4.4) можно представить в «компактной» форме записи:

Обычно такое описание линейных САУ (САР) используется в цифровых системах управления (с использованием ЭВМ).

4) Линейные системы автоматического управления с запаздыванием:

где L(p), N(p) — линейные дифференциальные операторы; τ — время запаздывания или постоянная запаздывания.

Если операторы L(p) и N(p) вырождаются (L(p) = 1; N(p) = 1), то уравнение (1.4.6) соответствует математическому описанию динамики звена идеального запаздывания:

а графическая иллюстрация его свойств привдена на рис. 1.4.1

5) Линейные системы автоматического управления, описываемые линейными дифференциальными уравнения в частных производных. Нередко такие САУ называют распределенными системами управления. ==> «Абстрактный» пример такого описания:

Система уравнений (1.4.7) описывает динамику линейно распределенной САУ, т.е. регулируемая величина зависит не только от времени, но и от одной пространственной координаты.
Если система управления представляет собой «пространственный» объект, то ==>

где зависит от времени и пространственных координат, определяемых радиусом-вектором

6) САУ, описываемые системами ОДУ, или системами разностных уравнений, или системами уравнений в частных производных ==> и так далее…

Аналогичную классификацию можно предложить и для нелинейных САУ (САР)…

Для линейных систем выполеняются следующие требования:

• линейность статической характеристики САУ;
• линейность уравнения динамики, т.е. переменные в уравнение динамики входят только в линейной комбинации.

Статической характеристикой называется зависимость выхода от величины входного воздействия в установившемся режиме (когда все переходные процессы затухли).

Для систем, описываемых линейными обыкновенными дифференциальными уравнениями с постоянными коэффициентами статическая характеристика получается из уравнения динамики (1.4.1) приравниванием нулю всех нестационарных членов ==>

На рис.1.4.2 представлены примеры линейной и нелинейных статических характеристик систем автоматического управления (регулирования).

Нелинейность членов, содержащих производные по времени в уравнениях динамики, может возникнуть при использовании нелинейных математических операций (*, /, , , sin, ln и т.д.). Например, рассматривая уравнение динамики некоторой «абстрактной» САУ

отметим, что в этом уравнении при линейной статической характеристики второе и третье слагаемые (динамические члены) в левой части уравнения — нелинейные, поэтому САУ, описываемая подобным уравнением, является нелинейной в динамическом плане.

1.4.2. Классификация по характеру передаваемых сигналов

По характеру передаваемых сигналов системы автоматического управления (или регулирования) подразделяются:

• непрерывные системы (системы непрерывного действия);
• релейные системы (системы релейного действия);
• системы дискретного действия (импульсные и цифровые).

Системой непрерывного действия называется такая САУ, в каждом из звеньев которой непрерывному изменению входного сигнала во времени соответствует непрерывное изменение выходного сигнала, при этом закон изменения выходного сигнала может быть произвольным. Чтобы САУ была непрерывной, необходимо, чтобы статические характеристики всех звеньев были непрерывными.

Системой релейного действия называется САУ, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина в некоторые моменты процесса управления меняется “скачком” в зависимости от величины входного сигнала. Статическая характеристика такого звена имеет точки разрыва или излома с разрывом.

Системой дискретного действия называется система, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина имеет вид отдельных импульсов, появляющиеся через некоторый промежуток времени.

Звено, преобразующее непрерывный сигнал в дискретный сигнал, называется импульсным. Подобный вид передаваемых сигналов имеет место в САУ с ЭВМ или контроллером.

Наиболее часто реализуются следующие методы (алгоритмы) преобразования непрерывного входного сигнала в импульсный выходной сигнал:

• амплитудно-импульсная модуляция (АИМ);
• широтно-импульсная модуляция (ШИМ).

На рис. 1.4.5 представлена графическая иллюстрация алгоритма амплитудно-импульсной модуляции (АИМ). В верхней части рис. представлена временная зависимость x(t) — сигнала на входе в импульсное звено. Выходной сигнал импульсного блока (звена) y(t) – последовательность прямоугольных импульсов, появляющихся с постоянным периодом квантования Δt (см. нижнюю часть рис.). Длительность импульсов – одинакова и равна Δ. Амплитуда импульса на выходе блока пропорциональна соответствующей величине непрерывного сигнала x(t) на входе данного блока.

Данный метод импульсной модуляции был весьма распространен в электронно-измерительной аппаратуре систем управления и защиты (СУЗ) ядерных энергетических установок (ЯЭУ) в 70-х…80-х годах прошлого столетия.

На рис. 1.4.6 представлена графическая иллюстрация алгоритма широтно-импульсной модуляции (ШИМ). В верхней части рис. 1.14 представлена временная зависимость x(t) – сигнала на входе в импульсное звено. Выходной сигнал импульсного блока (звена) y(t) – последовательность прямоугольных импульсов, появляющихся с постоянным периодом квантования Δt (см. нижнюю часть рис. 1.14). Амплитуда всех импульсов – одинакова. Длительность импульса Δt на выходе блока пропорциональна соответствующей величине непрерывного сигнала x(t) на входе импульсного блока.

Данный метод импульсной модуляции в настоящее время является наиболее распространенным в электронно-измерительной аппаратуре систем управления и защиты (СУЗ) ядерных энергетических установок (ЯЭУ) и САУ других технических систем.

Завершая данный подраздел, необходимо заметить, что если характерные постоянные времени в других звеньях САУ (САР) существенно больше Δt (на порядки), то импульсная система может считаться непрерывной системой автоматического управления (при использовании как АИМ, так и ШИМ).

1.4.3. Классификация по характеру управления

По характеру процессов управления системы автоматического управления подразделяются на следующие типы:

• детерминированные САУ, в которых входному сигналу однозначно может быть поставлен в соответствие выходной сигнал (и наоборот);
• стохастические САУ (статистические, вероятностные), в которых на данный входной сигнал САУ “отвечает” случайным (стохастическим) выходным сигналом.

Выходной стохастический сигнал характеризуется:

• законом распределения;
• математическим ожиданием (средним значением);
• дисперсией (среднеквадратичным отклонением).

Стохастичность характера процесса управления обычно наблюдается в существенно нелинейных САР как с точки зрения статической характеристики, так и с точки зрения (даже в большей степени) нелинейности динамических членов в уравнениях динамики.

Кроме приведенных основных видов классификации систем управления, существуют и другие классификации. Например, классификация может проводиться по методу управления и основываться на взаимодействии с внешней средой и возможности адаптации САУ к изменению параметров окружающей среды. Системы делятся на два больших класса:

1) Обыкновенные (несамонастраивающиеся) СУ без адаптации; эти системы относятся к разряду простых, не изменяющих свою структуру в процессе управления. Они наиболее разработаны и широко применяются. Обыкновенные СУ подразделяются на три подкласса: разомкнутые, замкнутые и комбинированные системы управления.

2) Самонастраивающиеся (адаптивные) СУ. В этих системах при изменении внешних условий или характеристик объекта регулирования происходит автоматическое (заранее не заданное) изменение параметров управляющего устройства за счет изменения коэффициентов СУ, структуры СУ или даже введения новых элементов.

Другой пример классификации: по иерархическому признаку (одноуровневые, двухуровневые, многоуровневые).

Видео:Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

РАЗОМКНУТЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Состояние объекта управления характеризуется совокупностью физических величин, которые называют также показателями, параметрами, координатами процесса. Например: температура, давление, скорость, ток, напряжение.

Для нормального хода технологического процесса некоторые из его координат – управляемые координаты – необходимо поддерживать постоянными (напряжение генератора, скорость электродвигателя, давление компрессора и др.), либо изменять во времени по заданному закону (скорость подъёмной установки при её пуске и остановке).

Необходимость в управлении значениями координат возникает в том случае, когда нормальный ход процесса нарушается из-за различного рода возмущений, т.е. колебаний нагрузки, воздействий внешней среды или внутренних помех.

Сами машины или устройства во многих случаях не обладают способностью поддерживать постоянство координат или изменять их по заданному закону.

Управление, которое автоматически поддерживает координаты технологического процесса неизменными или изменяет их по заданному закону, называется регулированием.

Система автоматического управления, которая в течение длительного времени автоматически поддерживает координаты технологического процесса неизменными или изменяет их по заданному закону называется системой автоматического регулирования(САР).

Система автоматического регулирования является замкнутой системой, или системой с обратной связью.

РАЗОМКНУТЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Автоматические системы управления отличаются одна от другой объектами и целями управления, физической природой и конструкциями элементов управляющих устройств. Тем не менее вне зависимости от их различий все системы управления можно разделить на два больших класса – разомкнутые и замкнутые.

На рис. 2.1, а показана функциональная схема разомкнутой САУ.

Рассмотрим назначение и свойства отдельных элементов функциональной схемы:

1. ОУ – объект управления. Это объект, которым управляют: электродвигатель, буровой станок и т. д.

Параметр производственного процесса , которым мы хотим управлять, носит название управляемой или регулируемой величины. Регулируемую величину всегда принимают за выходную величину объекта управления. Вследствие большого разнообразия управляемых объектов физическая природа регулируемого параметра производственного процесса различна. Он может представлять собой угловую скорость электродвигателя, температуру, давление и расход жидкости или газа, напряжение генератора и т. д.

На объект управления поступают два входных воздействия: возмущающее f(t ) и управляющее u(t ).

Возмущающее воздействие – это воздействие, которое не зависят от управляющего устройства.

Управляющее воздействие – это воздействие, которое вырабатывается управляющим устройством УУ и поступает непосредственно на вход объекта управления.

Рис. 1.1.4 (а)

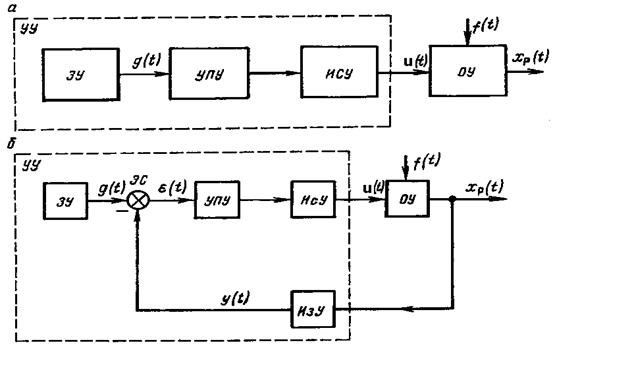Рис. 2.1. Функциональные схемы разомкнутой (а) и замкнутой (б) САУ

2. ИСУ – исполнительное устройство. Оно непосредственно воздействует на объект управления. Выходной величиной исполнительного устройства является управляющее воздействие u(t), поступающее на вход объекта управления. Мощность исполнительного устройства обычно велика, так как оно воздействует непосредственно на объект управления.

3. УПУ – усилительно-преобразовательное устройство. Предназначено для усиления мощности и преобразования сигналов в управляющем устройстве.

4. ЗУ – задающее устройство (задатчик регулируемой величины). Выходной величиной задающего устройства является задающее воздействие (сигнал задания) g(t).

Задающее воздействие g(t) – это воздействие, которое задаёт требуемое значение регулируемой величины .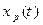

Энергия, необходимая для установки задающего воздействия, как правило, мала по сравнению с энергией, необходимой для работы исполнительного устройства и объекта управления.

Задающее, усилительно-преобразовательное и исполнительное устройства являются основными элементами управляющего устройства УУ.

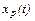
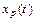
Управляющее воздействие u(t) устанавливает заданное значение регулируемой величины . Возмущающее воздействие f(t) вызывает отклонение регулируемой величины от заданного значения. Главный недостаток разомкнутых систем – отсутствие информации об объекте управления. Это может привести к значительному отклонению регулируемой величины от заданного значения при действии возмущающего воздействия и возникновению аварийной ситуации.

Несмотря на указанный недостаток область применения разомкнутых систем управления достаточно велика. Примерами разомкнутых систем являются системы автоматического пуска, остановки и реверсирования машин и механизмов, где не требуется точного регулирования скорости.

Для того чтобы автоматически уменьшить отклонение регулируемой величины от заданного значения при действии на объект управления возмущающего воздействия, необходимо применение замкнутой САУ. Замкнутая САУ содержит дополнительную связь, по которой результат измерения регулируемой величины передаётся на вход системы управления. Эта связь называется обратной связью по регулируемой величине, так как направление передачи воздействия в дополнительной связи обратно направлению передачи основного воздействия на объект.

Система управления, имеющая обратную связь по регулируемой величине, называется системой с обратной связью, илизамкнутой системой.

На рис. 2.1, б приведена функциональная схема замкнутой САУ. По сравнению с разомкнутой системой здесь управляющее устройство УУ содержит два дополнительных элемента: измерительное устройство ИЗУ и элемент сравнения ЭС.

Измерительное устройство (датчик) измеряет действительное значение управляемой величины и преобразует его в выходной сигнал, удобный для ввода в систему управления.

Выходной сигнал измерителя 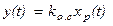называется сигналом обратной связи по регулируемой величине, а коэффициент пропорциональности k_о.с –коэффициентом обратной связи по регулируемой величине. Сигнал обратной связи y(t) подается на вход элемента сравнения ЭС, где сравнивается с сигналом задания g(t). Физическая природа сигналов обратной связи и задания должна быть одинакова.

Элемент сравнения служит для определения величины отклонения регулируемой величины от заданного значения. Выходной величиной элемента сравнения является разность e(t ) двух входных сигналов g(t ) и y(t ):

.

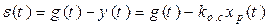
Величина e(t) пропорциональна отклонению регулируемой величины от заданного значения и называется ошибкой регулирования. Ошибка e(t) является источником воздействия на систему. В этом случае САУ работает таким образом, чтобы уничтожить или свести к минимальному значению отклонение регулируемой величины от заданного значения при действии на объект управления возмущения f(t).

Обратим внимание на то, что в случае замкнутой САУ сигнал обратной связи должен подаваться на вход ЭС со знаком, противоположным знаку сигнала задания g(t). В этом случае обратная связь по регулируемой величине называется отрицательной.

Если сигнал обратной связи подается на вход ЭС с тем же знаком, что и сигнал задания, т.е. складывается с ним, то обратная связь называется положительной.

При подаче на вход ЭС сигнала отрицательной обратной связи (ООС) на схеме рядом с этим входом ставится знак «–» (рис 2.1, б). В случае положительной обратной связи (ПОС) знак «+» может опускаться.

Отрицательнаяобратная связь по регулируемой величине x_р уменьшает ошибку регулирования e при действии на объект управления возмущающего воздействия f.

Положительная обратная связь по регулируемой величине x_р увеличивает ошибку регулирования e при действии на объект управления возмущающего воздействия f.

Только применяя отрицательные обратные связи по регулируемым величинам, возможно решить задачу автоматического регулирования – автоматически поддерживать параметры технологического процесса неизменными или изменять их по заданному закону с требуемой точностью независимо от действия возмущающих воздействий.

В зависимости от характера изменения задающего воздействия во времени все системы автоматического регулирования делятся на три класса – стабилизации, программные и следящие.

Система стабилизации – это такая система, в которой значение задающего воздействия постоянно, не меняется во времени:

Системы стабилизации применяют для поддержания постоянства физических величин, характеризующих состояние объекта управления. Примером системы стабилизации является система регулирования давления компрессорной установки.

Программная автоматическая система – это такая система, в которой задающее воздействие является заранее заданной функцией времени g(t).

Программной системой является автоматическая система управления подъемной установкой, которая должна формировать требуемую диаграмму скорости подъёмного сосуда.

Следящая автоматическая система – это такая система, в которой закон изменения задающего воздействия заранее неизвестен. Следящие системы используют обычно для перемещения объектов в пространстве. Управляемой величиной в этом случае является либо расстояние перемещаемого объекта от какой-либо начальной точки, либо угол поворота вращаемого объекта относительно начального положения.

Цель управления в стабилизирующих, программных и следящих системах – это обеспечение равенства или близости регулируемой величины к её заданному значению.

🔥 Видео

Построить структурную схему САР (САУ) по передаточной функцииСкачать

Настройка ПИД регулятора на практикеСкачать

Теория автоматического управления. Лекция 10. Критерий МихайловаСкачать

Программирование станков с ЧПУ. Объясняем просто и понятноСкачать

Теория автоматического управления. Лекция 7. Типовые звенья САУСкачать

Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Урок 3. JavaScript. Что такое замыкания. Как они работают (+ примеры)Скачать

Метод пространства состояний САУ: описание конкретной системыСкачать

Линейные системы автоматического регулирования. Лекция 1. Классификация САУСкачать

Преобразование структурных схем систем управленияСкачать

Теория автоматического регулирования. Лекция 3. Временные характеристики САУСкачать

[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать