Обобщенный закон Гука завершает вывод основных уравнений линейной теории упругости. Теперь мы имеем возможность рассмотреть все эти уравнения с точки зрения постановки и решения соответствующей краевой задачи о деформировании твердого тела.
1.6.1. Сводка основных уравнений теории упругости. Классификация граничных задач. Выпишем еще раз основные уравнения, полученные при исследовании статической, геометрической и физической сторон процесса деформирования упругого тела.
уравнения локального равновесия (уравнения Навье см.(1.11)) —
(1.37)
статические граничные условия (1.9) —
(1.38)
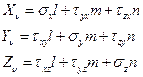
соотношения Коши (3.17)—
(1.39)
уравнения совместности деформаций (уравнения Сен-Венана (3.30))
(1.40)
Физические уравнения: обобщенный закон Гука (1.34)
(1.41)
или в обратной форме (1.37)
(1.42)
В рамках линейной теории совокупность уравнений (1.37), (1.41) образует математическую модель упруго деформируемого тела.
Наша ближайшая цель — формулировка краевой задачи. В связи с этим напомним, что под краевой задачей понимается задача отыскания одной или нескольких функций, являющихся решением одного или нескольких дифференциальных (или иных) уравнений (обыкновенных или в частных производных) и удовлетворяющих краевым условиям — условиям на границе области.
В теории упругости (как и в других физических науках) дифференциальные уравнения краевой задачи часто называют разрешающими уравнениями, что объясняется тем, что они получаются в результате преобразования (разрешения) уравнений, составляющих математическую модель процесса деформирования упругого тела, к системе с меньшим числом уравнений. Система разрешающих уравнений краевой задачи выполняется внутри области. Поэтому вывод ее следует проводить с помощью уравнений, справедливых для внутренних точек тела. Таковыми являются (1.37) – (1.41) за исключением уравнений (1.38).
Видео:Эглит М.Э.-Основы механики сплошных сред - 17. Уравнения Навье-ЛамеСкачать
Для деформируемых тел можно ставить два типа краевых (граничных) условий: статические и геометрические. Первые формулируются для напряжений и ими, по существу, являются уравнения (1.38). Что касается геометрических граничных условий, то постановка их сводится к заданию компонент смещения на всей границе тела или же на ее части в зависимости от связей, накладываемых на тело в процессе деформирования.
Пусть 
— часть поверхности тела, на которой заданы смещения. Тогда геометрические граничные условия имеют вид
(1.43)
где 
— заданная векторная функция, а 
— радиус-вектор точек поверхности .
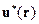
По типу краевых условий, но независимо от вида разрешающих уравнений, в теории упругости различают три граничные задачи.
Первая основная граничная задача формулируется так: по заданным внешним силам найти напряженно-деформированное состояние в теле, если на всей его границе ставятся только статические граничные условия.
Во второй граничной задаче на всей границе тела формулируются только геометрические граничные условия.
В случае третьей основной граничной задачи на поверхности тела задаются граничные условия обоих типов. По этой причине ее часто называют смешанной граничной задачей теории упругости.
Вид разрешающих уравнений зависит от того, какие величины выбраны за основные неизвестные. В связи с этим в теории упругости утвердились три метода решения задач: метод перемещений, метод напряжений и смешанный метод. В первом методе за неизвестные принимаются компоненты перемещения во втором — напряжения. В смешанном методе — как статические, так и геометрические величины.
Остановимся подробно на первых двух методах.
1.6.2. Метод перемещений. Примем за основные неизвестные, описывающие процесс деформирования упругого тела, компоненты перемещения 
, 
, 
. При выводе системы разрешающих уравнений необходимо позаботиться о том, чтобы удовлетворялись все уравнения линейной теории упругости (1.37)-(1.41).
Предположим, что мы получили систему разрешающих уравнений, и нашли ее решение — функции 
, 
, 
. Для вычисления деформаций надо воспользоваться соотношениями Коши. Как отмечалось, при этом уравнения совместности деформаций выполняются сами по себе. Следовательно, разрешающие уравнения метода перемещений должны вытекать из уравнений (1.37), (1.39) и (1.42). Чтобы получить их, необходимо, прежде всего, выразить напряжения и деформации через перемещения.
(1.44)
(1.45)
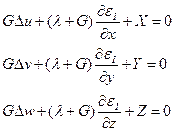
— дифференциальный оператор Лапласа.
Уравнения (1.44) называются уравнениями Ламе и образуют искомую систему разрешающих уравнений метода перемещений. Они синтезируют в себе статическую, геометрическую и физическую стороны процесса деформирования. Действительно, по своему существу — это уравнения равновесия в перемещениях. Наличие в них упругих постоянных 
и 
свидетельствует об их связи с физическими свойствами упругого тела.
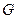
Уравнения Ламе совместно с заданными геометрическими граничными условиями (1.43) и статическими условиями на поверхности (1.38), которые, предварительно, следует представить в перемещениях путем подстановки в них уравнений (1.6), образуют краевую задачу метода перемещений. По найденным в результате ее решения перемещениям напряженно-деформированное состояние тела определяется формулами (1.39) и (1.42).
1.6.3. Метод напряжений. Примем теперь за основные неизвестные напряжения 
, 
, 
, 
, 
, 
. Эти шесть величин должны удовлетворять, прежде всего, уравнениям равновесия (1.37). Выше уже отмечалось, что общая задача теории упругости статически неопределима. Это означает, что уравнений равновесия и статических граничных условий недостаточно (даже в случае первой основной задачи) для однозначного определения напряженного состояния в теле.
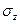
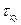
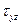
Обобщенный закон Гука устанавливает однозначную линейную зависимость между напряжениями и деформациями. Но последние должны удовлетворять условиям совместности деформаций. Следовательно, и напряжения должны быть связаны между собой некоторыми соотношениями, гарантирующими выполнение условий (1.40).
Для установления зависимостей между напряжениями достаточно подставить (1.41) в (1.40) и преобразовать последние с учетом уравнений равновесия (1.37).
В результате получим
(1.46)
Здесь, напомним, 
Уравнения (1.46) и (1.37) образуют систему разрешающих уравнений метода напряжений. Уравнения (1.46) принято называть тождествами (уравнениями) Бельтрами-Мичелла. Они синтезируют в себе все три стороны процесса деформирования, ибо являются условиями сплошности в напряжениях и получены с учетом уравнений равновесия и обобщенного закона Гука.
Видео:выпуск 3 [ толстостенные трубы. задача Ламе ]Скачать
![выпуск 3 [ толстостенные трубы. задача Ламе ]](https://i.ytimg.com/vi/CrfvNqQcDFo/0.jpg)
Лекция 1. Основы теории упругости
1.1 Основные положения, допущения и обозначения
Теория упругости имеет целью аналитическое изучение напряженно-деформированного состояния упругого тела. С помощью теории упругости могут быть проверены решения, полученные с использованием допущений сопротивления материалов, и установлены границы применимости этих решений. Иногда разделы теории упругости, в которых, как и в сопротивлении материалов, рассматривается вопрос о пригодности детали, но с использованием достаточно сложного математического аппарата (расчет пластин, оболочек, массивов), относят к прикладной теории упругости.
В настоящей главе изложены основные понятия математической линейной теории упругости. Применение математики к описанию физических явлений требует их схематизации. В математической теории упругости задачи решаются с возможно меньшим числом допущений, что усложняет математические приемы, применяемые для решения. В линейной теории упругости предполагается существование линейной зависимости между составляющими напряжениями и деформациями. Для ряда материалов (резина, некоторые сорта чугуна) такая зависимость даже при малых деформациях не может быть принята: диаграмма s — e в пределах упругости имеет одинаковые очертания как при нагружении , так и при разгрузке, но в обоих случаях криволинейна. При исследовании таких материалов необходимо пользоваться зависимостями нелинейной теории упругости.
В математической линейной теории упругости исходят из следующих допущений:
1. О непрерывности ( сплошности ) среды. При этом атомистическая структура вещества или наличие каких-либо пустот не учитывается.
2. О естественном состоянии, на основании которого начальное напряженное (деформированное) состояние тела, возникшее до приложения силовых воздействий, не учитывается, т. е. предполагается, что в момент нагружения тела деформации и напряжения в любой его точке равны нулю. При наличии начальных напряжений это допущение будет справедливым, если только к результирующим напряжениям (сумме начальных и возникших от них из воздействий) могут быть применены зависимости линейной теории упругости.
3. Об однородности, на основании которого предполагается, что состав тела одинаков во всех точках. Если применительно к металлам это допущение не дает больших погрешностей, то в отношении бетона при рассмотрении малых объемов оно может привести к значительным погрешностям.
4. О шаровой изотропности , на основании которого считается, что механические свойства материала одинаковы по всем направлениям. Кристаллы металла не обладают таким свойством, но для металла в целом, состоящего из большого числа мелких кристаллов, можно считать, что эта гипотеза справедлива. Для материалов, обладающих различными механическими свойствами в разных направлениях, как, например, для слоистых пластиков, разработана теория упругости ортотропных и анизотропных материалов.
5. Об идеальной упругости, на основании которого предполагается полное исчезновение деформации после снятия нагрузки. Как известно, в реальных телах при любом нагружении возникает остаточная деформация. Поэтому допущение следует считать применимым, если остаточная деформация не превышает условно заданной нормы.
6. О линейной зависимости между составляющими деформациями и напряжениями.
7. О малости деформаций, на основании которого предполагается, что относительные линейные и угловые деформации малы по сравнению с единицей. Для таких материалов, как резина, или таких элементов, как спиральные пружины, создана теория больших упругих деформаций.
При решении задач теории упругости пользуются теоремой о единственности решения: если заданные внешние поверхностные и объемные силы находятся в равновесии, им соответствует одна единственная система напряжений и перемещений. Положен ие о е динственности решения справедливо, если только справедливы допущение о естественном состоянии тела (иначе возможно бесчисленное количество решений) и допущение о линейной зависимости между деформациями и внешними силами.
Видео:Сопротивление материалов. Лекция: Задача ЛамеСкачать
При решении задач теории упругости часто пользуются принципом Сен-Венана: если внешние силы, приложенные на небольшом участке упругого тела, заменить действующей на том же участке статически эквивалентной системой сил (имеющей тот же главный вектор и тот же главный момент), то эта замена вызовет лишь изменение местных деформаций.
В точках, достаточно удаленных от мест приложения внешних нагрузок, напряжения мало зависят от способа их приложения. Нагрузка, которая в курсе сопротивления материалов схематически выражалась на основании принципа Сен-Венана в виде силы или сосредоточенного момента, на самом деле представляет собой нормальные и касательные напряжения, распределенные тем или иным способом на определенном участке поверхности тела. При этом одной и той же силе или паре сил может соответствовать различное распределение напряжений. На основании принципа Сен-Венана можно считать, что изменение усилий на участке поверхности тела почти не отражается на напряжениях в точках, удаленных на достаточно большое расстояние от места приложения этих усилий (по сравнению с линейными размерами нагруженного участка).
Положение исследуемой площадки, выделенной в теле (рис. 1), определяется направляющими косинусами нормали N к площадке в выбранной системе прямоугольных осей координат х , у и z .
Если 
Р — равнодействующая внутренних сил, действующих по элементарной площадке 
, выделенной у точки А , то полное напряжение р N в этой точке по площадке с нормалью N определяется как предел отношения в следующей форме:
.
Вектор р N можно разложить в пространстве на три взаимно перпендикулярные составляющие.
1. На составляющие р Nx , р Ny и р Nz по направлениям трех осей (рис. 1, а). Эти составляющие положительны, если совпадают по направлению с положительными направлениями соответствующих осей. Согласно рис. 1, а
. (1.1,а)
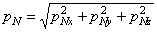
2. На составляющие 
, 
и 
по направлениям нормали к площадке (нормальное напряжение) и двух взаимно перпендикулярных осей s и t (рис. 1,б), лежащих в плоскости площадки (касательные напряжения). Согласно рис.1, б
. (1.1,б)
Если сечение тела или площадка параллельны одной из плоскостей координат, например у0 z (рис. 2), то нормалью к этой площадке будет третья ось координат х и составляющие напряжения будут иметь обозначения 
, 
и 
.
Нормальное напряжение положительно, если оно растягивающее, и отрицательно, если оно сжимающее. Знак касательного напряжения определяется с помощью следующего правила: если положительное (растягивающее) нормальное напряжение по площадке дает положительную проекцию, то касательное напряжение по той же площадке считается положительным при условии, что оно тоже дает положительную проекцию на соответствующую ось; если же растягивающее нормальное напряжение дает отрицательную проекцию, то положительное касательное напряжение тоже должно давать отрицательную проекцию на соответствующую ось.
На рис. 3, например, все составляющие напряжения, действующие по граням элементарного параллелепипеда, совпадающим с плоскостями координат, положительны.
Чтобы определить напряженное состояние в точке упругого тела, необходимо знать полные напряжения р N по трем взаимно перпендикулярным площадкам, проходящим через эту точку. Так как каждое полное напряжение можно разложить на три составляющие, напряженное состояние будет определено, если будут известны девять составляющих напряжений. Эти составляющие можно записать в виде матрицы
,
называемой матрицей компонентов тензора напряжений в точке.
В каждой горизонтальной строчке матрицы записаны три составляющих напряжения, действующих по одной площадке, так как первые значки (название нормали) у них одинаковые. В каждом вертикальном столбце тензора записаны три напряжения, параллельных одной и той же оси, так как вторые значки (название оси, параллельно которой действует напряжение) у них одинаковые.
1.2 Уравнения равновесия элементарного параллелепипеда и элементарного тетраэдра
Выделим у исследуемой точки А (с координатами х , у и z ) напряженного упругого тела тремя взаимно перпендикулярными парами плоскостей элементарный параллелепипед с размерами ребер dx , dy и dz (рис. 2). По каждой из трех взаимно перпендикулярных граней, примыкающих к точке А (ближайших к плоскостям координат), будут действовать три составляющих напряжения — нормальное и два касательных. Считаем, что по граням, примыкающим к точке А , они положительны.
При переходе от грани, проходящей через точку А , к параллельной грани напряжения меняются и получают приращения. Например, если по грани CAD , проходящей через точку А , действуют составляющие напряжения = f 1 ( x , y , z ), = f 2 ( x , y , z ,), = f 3 ( x , y , z ,), то по параллельной грани, вследствие приращения только одной координаты х при переходе от одной грани к другой, будут действовать составляющие напряжения 
Можно определить напряжения на всех гранях элементарного параллелепипеда, как показано на рис. 3.
Кроме напряжений, приложенных к граням элементарного параллелепипеда, на него действуют объемные силы: силы веса, инерционные. Обозначим проекции этих сил, отнесенных к единице объема, на оси координат через X, У и Z. Если приравнять нулю сумму проекций на ось х всех нормальных, касательных и объемной сил, действующих на элементарный параллелепипед, то после сокращения на произведение dxdydz получим уравнение
.
Видео:Закон Харди — Вайнберга | НОВАЯ тема ЕГЭ по Биологии | Популяционная генетикаСкачать
Составив аналогичные уравнения проекций сил на оси у и z , напишем три дифференциальных уравнения равновесия элементарного параллелепипеда, полученных Коши,
. (1.2)
При уменьшении размеров параллелепипеда до нуля он превращается в точку, а 
и 
представляют собой составляющие напряжения по трем взаимно перпендикулярным площадкам, проходящим через точку А.
Если приравнять нулю сумму моментов всех сил, действующих на элементарный параллелепипед, относительно оси x c , параллельной оси х и проходящей через его центр тяжести, получим уравнение
или, с учетом того, что второй и четвертый члены уравнения высшего порядка малости по сравнению с остальными, после сокращения на dxdydz
или 
.
Составив аналогичные уравнения моментов относительно центральных осей у c и zc , получим три уравнения закона парности касательных напряжений
, 
, 
. (1.3)
Этот закон формулируется так: касательные напряжения, действующие по взаимно перпендикулярным площадкам и направленные перпендикулярно к линии пересечения площадок, равны по величине и одинаковы по знаку.
Таким образом, из девяти составляющих напряжений матрицы тензора 
шесть попарно равны друг другу, и для определения напряженного состояния в точке достаточно найти лишь следующие шесть составляющих напряжений:
.
Но составленные условия равновесия дали нам всего лишь три уравнения (1.2), из которых шесть неизвестных найдены быть не могут. Таким образом, прямая задача определения напряженного состояния в точке в общем случае статически неопределима. Для раскрытия этой статической неопределимости необходимы дополнительные геометрические и физические зависимости.
Рассечем элементарный параллелепипед у точки А плоскостью, наклоненной к его граням; пусть нормаль N к этой плоскости имеет направляющие косинусы l , т и п. Получившаяся геометрическая фигура (рис. 4) представляет собой пирамиду с треугольным основанием — элементарный тетраэдр. Будем считать, что точка А совпадает с началом координат, а три взаимно перпендикулярные грани тетраэдра — с плоскостями координат.
Составляющие напряжения, действующие по этим граням тетраэдра, будем считать положительными. Они показаны на рис. 4. Обозначим через 
и 
проекции полного напряжения pN , действующего по наклонной грани BCD тетраэдра, на оси х , у и z . Площадь наклонной грани BCD обозначим dF . Тогда площадь грани АВС будет dF 
, грани ACD — dF 
и грани А D В — dF 
.
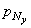
Составим уравнение равновесия тетраэдра, спроектировав все силы, действующие по его граням, на ось х ; проекция объемной силы в уравнение проекций не входит, так как представляет собой величину высшего порядка малости по сравнению с проекциями поверхностных сил:
,
.
Составив уравнения проекции сил, действующих на тетраэдр, на оси у и z , получим еще два аналогичных уравнения. В результате будем иметь три уравнения равновесия элементарного тетраэдра
. (1.4)
По известным трем проекциям найдем полное напряжение
. (1.5)
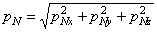
Разделим пространственное тело произвольной формы системой взаимно перпендикулярных плоскостей хОу , y О z и хО z (рис. 5) на ряд элементарных параллелепипедов. У поверхности тела при этом образуются элементарные тетраэдры, (криволинейные участки поверхности ввиду их малости можно заменить плоскостями). В таком случае р N будет представлять нагрузку на поверхности, а уравнения (1.4) будут связывать эту нагрузку с напряжениями и в теле, т. е. будут представлять граничные условия задачи теории упругости. Условия, определяемые этими уравнениями, называют условиями на поверхности.
Следует отметить, что в теории упругости внешние нагрузки представляются нормальными и касательными напряжениями, приложенными по какому-либо закону к площадкам, совпадающим с поверхностью тела.
1.3 Нормальные и касательные напряжения по наклонной площадке
Рассмотрим элементарный тетраэдр ABCD , три грани которого параллельны координатным плоскостям, а нормаль N к четвертой грани составляет с координатными осями углы, косинусы которых равны l , т и п (рис. 6). Будем считать заданными составляющие нормальные и касательные напряжения, действующие по площадкам, лежащим в координатных плоскостях, и определим напряжения на площадке BCD . Выберем новую систему прямоугольных осей координат х 1 , y 1 и z 1, так чтобы ось х1 совпадала с нормалью N , а оси у1 и z 1 лежали в плоскости площадки BCD . Каждая из этих осей будет иметь в системе осей x , y , z свои направляющие косинусы, указанные в табл. 1.
Видео:Решение задач на термохимические уравнения. 8 класс.Скачать
🎦 Видео
Принцип наименьшего действия #2 - Уравнение Эйлера-ЛагранжаСкачать
Лекция IV-3. Напряженное состояние под внешней нагрузкой. Часть 1Скачать
Система сходящихся сил. Решение задач по МещерскомуСкачать
Лекция №1 Постановка задачи теории упругости. Условия совместности деформаций Сен-Венана.Скачать
Горбачёв В. И. - Основы механики сплошных сред III - Метод ТФКП для случая плоской задачиСкачать
Леонтьев Н.Е. - Основы механики сплошных сред. Семинары - 7. Модель линейно-упругого телаСкачать
Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать
Сопротивление материалов. Лекция 1 (введение).Скачать
Сопротивление материалов. Лекция: тонкостенные оболочки вращения (исправленное видео)Скачать
Горбачёв В. И. - Основы механики сплошных сред III - Представление решений уравнений ЛямеСкачать
Решение биквадратных уравнений. 8 класс.Скачать
Сопротивление материалов. Лекция: устойчивость сжатых стержней, часть 1Скачать
