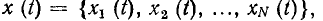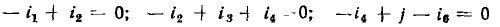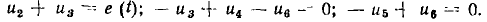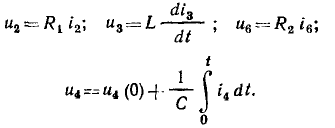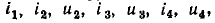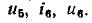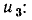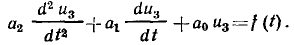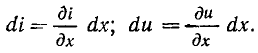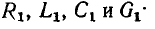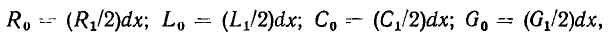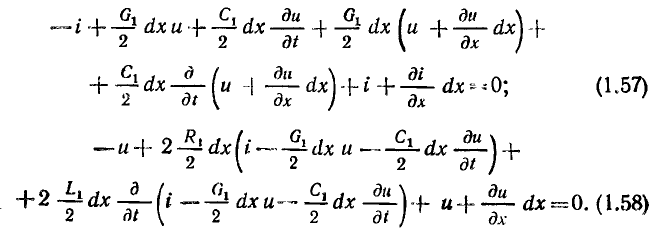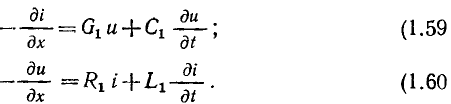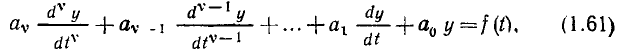Уравнения равновесия напряжений и токов

Содержание:

Уравнения электрического равновесия цепей:

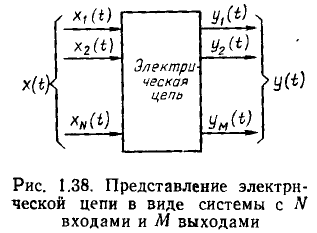
Любую электрическую цепь можно рассматривать как систему с одним или несколькими входами и одним или несколькими выходами (рис. 1.38). Если к входам цепи приложить внешнее воздействие

Задача анализа электрической цепи состоит в определении реакции цепи у (t) на заданное внешнее воздействие х (t).

Задача синтеза цепи заключается в нахождении цепи по заданной реакции цепи у (t) на некоторое внешнее воздействие х (t).

Исходными данными в задаче анализа являются эквивалентная схема цепи с параметрами всех входящих в нее элементов и описание внешнего воздействия х (t), задаваемого в виде совокупности токов и напряжений идеализированных неуправляемых источников. В результате анализа определяется отклик у (t) в виде совокупности токов и напряжений всех или некоторых ветвей цепи. 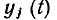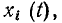В частном случае задача анализа может сводиться к определению соотношений между реакциями цепи на отдельных выходах и воздействиями приложенными к определенным входам. Такие соотношения называются характеристиками (системными функциями, функциями) цепи. В зависимости от того, какая величина— частота или время — является аргументом в выражениях, описывающих соотношения между откликом и внешним воздействием, различают частотные и временные характеристики цепи. Определение и исследование частотных характеристик представляют собой задачу анализа цепи в частотной области; нахождение временных характеристик — задачу анализа цепи во временной области.

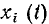
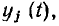
Исходными данными в задаче синтеза являются описания внешнего воздействия х (t) и ее отклика у (t). В результате синтеза необходимо найти эквивалентную схему цепи и параметры всех входящих в нее элементов. В частном случае задача синтеза может сводиться к нахождению цепи, обеспечивающей заданные соотношения между внешним воздействием на цепь и ее реакцией т. е. к нахождению цепи по ее характеристикам.

Анализ и синтез электрических цепей в определенной степени взаимосвязаны, в частности методы синтеза базируются на использовании общих свойств характеристик различных классов цепей, которые изучаются в процессе анализа. Поэтому изложению методов синтеза цепей будет предшествовать рассмотрение общих методов анализа цепей и знакомство с характеристиками некоторых классов цепей при различных внешних воздействиях.

Видео:Урок 358. Активное сопротивление в цепи переменного тока. Действующее значение тока и напряженияСкачать

Понятие об уравнениях электрического равновесия

Математически задача анализа электрической цепи сводится к составлению и решению системы линейно независимых уравнений, в которых в качестве неизвестных фигурируют токи и напряжения ветвей исследуемой цепи. Уравнения, решение которых позволяет определить токи и напряжения ветвей электрической цепи, называются уравнениями электрического равновесия цепи. Очевидно, что число уравнений электрического равновесия должно быть равно количеству неизвестных токов и напряжений.

В общем случае в цепи, содержащей р ветвей и q узлов, имеется 2р неизвестных токов и напряжений ветвей. Используя законы Кирхгофа, для такой цепи можно составить m = q— 1 независимых уравнений баланса токов и n = р — q + 1 независимых уравнений баланса напряжений. В сочетании с компонентными уравнениями (уравнениями ветвей) получаем 2р линейно независимых уравнений, что достаточно для определения неизвестных токов и напряжений ветвей.

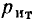
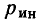
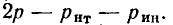
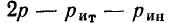
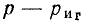
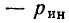
Если в рассматриваемой цепи имеется ветвей, в которых содержатся идеализированные источники тока (токи этих ветвей заданы, а напряжения неизвестны), и ветвей, составленных только из идеализированных источников напряжения (напряжения этих ветвей известны), то общее число неизвестных токов и напряжений уменьшается до Для определения этих неизвестных нужно составить лишь линейно независимых уравнений (m + n = р уравнений на основании законов Кирхгофа и компонентных уравнений для ветвей, не содержащих указанных источников).

Таким образом, используя компонентные уравнения и топологические уравнения, составленные на основании законов Кирхгофа, всегда можно сформировать систему уравнений электрического равновесия, число уравнений в которой достаточно для определения всех неизвестных токов и напряжений. Будем называть такую систему уравнений основной системой уравнений электрического равновесия цепи.

На практике для анализа цепей используют различные методы составления уравнения электрического равновесия, в частности методы токов ветвей, напряжений ветвей, контурных токов, узловых напряжений, переменных состояния. Все они базируются на использовании различных приемов, позволяющих преобразовать основную систему уравнений электрического равновесия и уменьшить по сравнению с 2р или 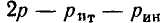число одновременно решаемых уравнений.

Как было показано ранее, уравнения (1.37) и (1.40) являются алгебраическими, а компонентные уравнения идеализированных пассивных элементов могут быть как алгебраическими (1.9), (1.10), так и дифференциальными (1.13), (1.22) или интегральными (1.16), (1.23).

Вследствие этого уравнения электрического равновесия цепи, составленные любым методом, представляют собой в общем случае систему интегродифференциальных уравнений.

Пример 1.7.

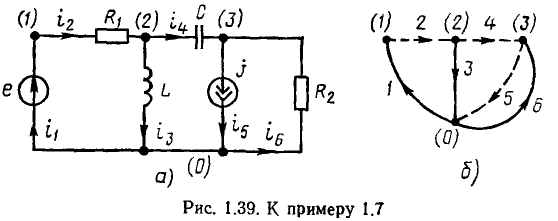
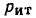
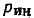
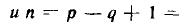
Составим основную систему уравнений электрического равновесия цепи, схема и топологический граф которой изображены на рис. 1.39, а и б соответственно. Для этой цепи р=6, q = 4, — 1 и = 1. Общее число неизвестных токов и напряжений ветвей Используя законы Кирхгофа, можно составить m = q — 1 = 3, уравнения баланса токов:

3 уровня баланса напряжений:

Кроме того, имеем 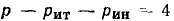уравнений ветвей, нес одержащих идеализированных источников:

В результате получаем систему из 10 линейно независимых уравнений для определения 10 неизвестных токов и напряжений:

Система уравнений электрического равновесия цепи, составленная любым методом, может быть путем дифференцирования и последовательного исключения неизвестных сведена к одному дифференциальному уравнению для любого из неизвестных токов и напряжений, называемому дифференциальным уравнением цепи. В частном случае это может быть алгебраическое уравнение, которое можно рассматривать как дифференциальное уравнение нулевого порядка. Дифференциальное уравнение цепи содержит фундаментальную информацию о характере имеющих место в цепи электрических процессов и является основой для классификации электрических цепей.Тип дифференциального уравнения цепи полностью определяется ее топологией и характером входящих в нее идеализированных элементов.

Пример 1.8.

Применяя указанные преобразования к основной системе уравнений электрического равновесия цепи (рис. 1.39, а), получим дифференциальное уравнение этой цепи, составленное относительно напряжения

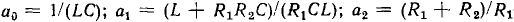
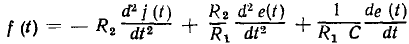
Здесь —постоянные коэффициенты, определяемые параметрами пассивных элементов цепи;

— Функция времени, определяемая параметрами независимых источников напряжения и тока.

Таким образом, уравнение цепи, изображенной на рис. 1.39, является линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами

Классификация электрических цепей

Электрические цепи, составленные из идеализированных элементов, могут быть классифицированы по ряду признаков:

по топологическим особенностям: планарные (плоские) и непланарные (объемные), разветвленные и неразветвленные, простейшие (одноконтурные, двухузловые) и сложные (многоконтурные, многоузловые);

по энергетическим свойствам: активные (содержащие идеализированные активные элементы) и пассивные (не содержащие идеализированных активных элементов);

по числу внешних выводов: двухполюсники и многополюсники; и др.

Классификация цепей по этим признакам не носит принципиального характера и используется, в основном, с целью упорядочения терминологии.

Фундаментальный характер имеет классификация цепей в зависимости от вида дифференциального уравнения цепи. Идеализированные электрические цепи, процессы в которых описываются обыкновенными дифференциальными уравнениями, называются цепями с сосредоточенными параметрами. Цепи такого типа используют в качестве упрощенных моделей реальных электрических цепей и их элементов на сравнительно низких частотах, когда длина волны электромагнитных колебаний существенно больше размеров исследуемого устройства. При этих условиях в исследуемых устройствах и их элементах удается выделить конечное число’ участков, в которых преобладает какой-то один из основных эффектов — запасание энергии электрического или магнитного полей, преобразование электрической энергии в другие виды энергии или преобразование энергии сторонних сил в электрическую. Токи рассматриваемой реальной цепи, являясь функциями времени, имеют одинаковые мгновенные значения в пределах каждого из выделенных участков. Заменяя эти участки идеализированными активными или пассивными элементами, получают идеализированную цепь, содержащую конечное число элементов, значения параметров которых конечны.

Таким образом, цепи с сосредоточенными параметрами представляют собой идеализированные цепи, моделирующие реальные устройства или их элементы при условиях, когда можно предположить, что каждый из основных электрических эффектов сосредоточен в конечном числе пространственно локализуемых областей.

Когда длина волны электромагнитных колебаний соизмерима с размерами исследуемого устройства или его элементов, пространственно локализовать области, в которых сосредоточены только эффекты одного типа, не удается. Это связано с тем, что даже при бесконечно малой длине выделяемых участков, в пределах каждого из них имеют место одновременно несколько из перечисленных основных эффектов, причем значения токов в пределах выделенных участков изменяются от одного сечения к другому.

При этих условиях цепи, моделирующие реальные устройства или их элементы, содержат бесконечно большое число идеализированных элементов, параметры которых имеют бесконечно малые значения. Процессы в таких цепях описываются дифференциальными уравнениями в частных производных. Идеализированные электрические цепи, процессы в которых описываются дифференциальными уравнениями в частных производных, называются цепями с распределенными параметрами.

Следует подчеркнуть, что термины «цепь с распределенными параметрами» и «цепь с сосредоточенными параметрами» применимы только к идеализированным (моделирующим) цепям и не должны использоваться для характеристики реальных цепей.

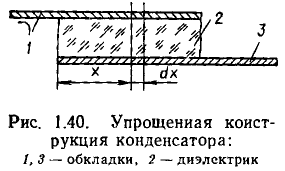
В зависимости от условий и требуемой точности исследования каждый элемент реальной цепи и, следовательно, каждая реальная цепь в целом могут быть заменены моделирующей цепью с сосредоточенными или распределенными параметрами. Например, конденсатор любого типа конструктивно представляет собой две проводящие обкладки 1 и 3, разделенные слоем диэлектрика 2 (рис. 1.40). В области частот, когда длина волны электромагнитных колебаний значительно превышает геометрические размеры обкладок, он может быть представлен одной из моделирующих цепей с сосредоточенными параметрами, схемы которых приведены на рис. 1.11. На более высоких частотах, когда длина волны электромагнитных колебаний сравнима с геометрическими размерами обкладок, но существенно больше расстояния между ними, необходимо учитывать, что процессы запасания энергии электрического и магнитного полей, а также необратимое преобразование электрической энергии в другие виды энергии имеют место вдоль всей длины обкладок конденсатора. 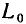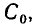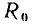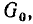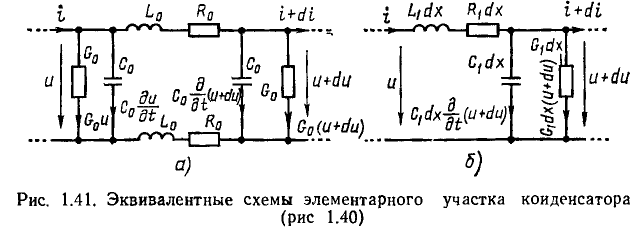В этом случае эквивалентная схема элементарного участка конденсатора длиной dx состоит из индуктивности и емкости характеризующих процессы запасания энергии магнитного и электрического полей, а также сопротивления и проводимости утечки учитывающих потери энергии в конденсаторе (рис. 1.41, а). Эквивалентная схема всего конденсатора должна состоять из бесконечно большого числа таких секций. Следовательно, идеализированная цепь, моделирующая конденсатор в рассматриваемом диапазоне частот, представляет собой цепь с распределенными параметрами.

На примере цепи, эквивалентная схема которой изображена на рис. 1.41, а, покажем, что электрические процессы в цепях с распределенными параметрами описываются дифференциальными уравнениями в частных производных. Действительно, ток i = i (х, t) и напряжение u = u (х, t) рассматриваемой цепи являются функциями времени t и координаты х.

Приращения тока и напряжения на участке цепи длиной dx

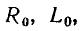
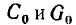
Полагая, что параметры элементов моделирующей цепи не зависят от токов и напряжений и выражая их через погонные (т. е. приходящиеся на единицу длины) параметры

составим уравнения баланса токов и напряжений элементарного участка цепи:

Пренебрегая величинами второго порядка малости, уравнения (1.57), (1.58) можно преобразовать к виду

Решая уравнения (1.59), (1.60) при соответствующих начальных граничных условиях, можно определить токи и напряжения цепи моделирующей коденсатор в рассматриваемом режиме.

Отметим, что уравнениям (1.59), (1.60) может быть поставлена в соответствие более простая эквивалентная схема элементарного участка цепи (рис. 1.41, б). Аналогичный вид имеют высокочастотные схемы замещения и ряда других элементов, входящих в состав радиоэлектронных устройств, в частности двухпроводных и коаксиальных линий передачи.

В зависимости от числа координат, вдоль которых происходит изменение тока и напряжения и вдоль которых «распределены» параметры цепи, различают одномерные, двухмерные и трехмерные цепи с распределенными параметрами. В теории цепей рассматривают, в основном, одномерные цепи с распределенными параметрами, процессы в которых описываются дифференциальными уравнениями типа (1.59), (1.60).

Параметры рассмотренных ранее идеализированных линейных пассивных элементов не зависят от значений токов и напряжений соответствующих элементов и, следовательно, от интенсивности внешнего воздействия на цепь, определяемой токами действующих в цепи независимых источников тока и напряжениями действующих в цепи независимых источников напряжения. Связь между током и напряжением линейных идеализированных пассивных элементов описывается линейными алгебраическими, дифференциальными или интегральными уравнениями, иными словами, компонентные уравнения этих элементов являются линейными.

Параметры нелинейных пассивных элементов зависят от токов или напряжений соответствующих элементов, а следовательно, и от интенсивности внешнего воздействия. Компонентные уравнения нелинейных идеализированных пассивных элементов — нелинейные.

В зависимости от вида компонентного уравнения идеализированные активные элементы также делятся на линейные и нелинейные. К линейным идеализированным активным элементам относят независимые в линейно управляемые зависимые источники тока и напряжения, к нелинейным — нелинейно управляемые зависимые источники тока г напряжения.

Цепь с сосредоточенными или распределенными параметрами, составленная только из линейных идеализированных элементов, называется линейной. Дифференциальное уравнение такой цепи — линейное. Если в состав цепи входит хотя бы один нелинейный пассив ими или активный элемент, то она называется нелинейной, а процессы в ней описываются нелинейными дифференциальными уравнениями.

Параметры линейных идеализированных пассивных элементов и коэффициенты управления линейно управляемых источников могут либо иметь постоянные значения, либо изменяться во времени под действием некоторых факторов, непосредственно не связанных с токами или напряжениями этих элементов (например, емкость конденсатора может изменяться во времени вследствие изменения расстояния между обкладками; индуктивность катушки можно изменять путем перемещения сердечника). Идеализированные элементы первого типа называют линейными элементами с постоянными параметрами, элементы второго типа — линейными элементами с переменными параметрами. Параметрические изменение параметров происходит с частотой. линейным а м а элементы, у близкой к частоте токов или напряжений этих элементов, следует отличать от регулируемых элементов —конденсаторов переменной емкости, вариометров, подстроечных конденсаторов и др., у которых изменение параметров производится весьма медленно и только в процессе настройки или регулировки соответствующего устройства.

При составлении уравнений электрического равновесия параметрам регулируемых элементов приписывают некоторые фиксированные значения, а сами элементы относят к элементам с постоянными параметрами.

Цепи, составленные только из линейных элементов с постоянными параметрами, называются линейными цепями с постоянными параметрами или линейными инвариантными во времени цепями. Процессы в линейных инвариантных во времени цепях описываются линейными уравнениями с постоянными коэффициентами.

Линейные цепи, содержащие хотя бы один элемент с переменными параметрами, называются линейными параметрическими цепями. Процессы в линейных параметрических цепях описываются линейными уравнениями с переменными коэффициентами.

В общем случае дифференциальное уравнение линейной цепи с сосредоточенными параметрами имеет следующий вид:

где у — искомая реакция цепи (ток или напряжение какой-либо ветви); 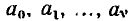— коэффициенты, определяемые параметрами пассивных элементов и коэффициентами управления управляемых источников. В дифференциальном уравнении линейной инвариантной во времени цепи эти коэффициенты постоянны, в дифференциальном уравнении линейной параметрической цепи, по крайней мере, один из них является функцией времени.

Правая часть уравнения (1.61) есть линейная комбинация функций, описывающих внешнее воздействие на цепь х (t), и их производных. При выключении всех источников она становится равной нулю.

Значение v характеризует порядок сложности цепи (порядок цепи) и равно числу реактивных элементов (емкостей и индуктивностей), энергетическое состояние которых может быть задано независимо (подробнее этот вопрос будет рассмотрен в гл. 6). Различают цепи нулевого порядка (не содержащие реактивных элементов), первого, второго и более высоких порядков.

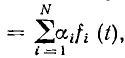
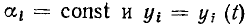
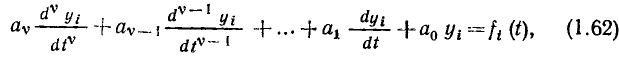
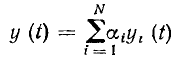
Для линейных уравнений вида (1.61) сформулирована теорема наложения (теорема суперпозиции). Если f(t) где являются решениями уравнений

то является решением уравнения (1.61).

Математически это значит, что решение линейного уравнения (1.61) со сложной правой частью можно выразить через решения уравнений (1.62) с более простой правой частью.

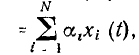
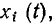
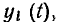
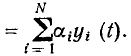
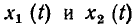
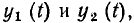
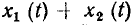
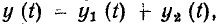
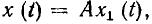
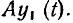
На теореме наложения базируется широко используемый в теории цепей принцип наложения (принцип суперпозиции): реакция у (t) линейной цепи на сложное воздействие х (t) представляющее собой линейную комбинацию более простых воздействий равна линейной комбинации реакций вызванных каждым из простых воздействий в отдельности, у (t) В частности, если внешним воздействиям соответствуют реакции то внешнему воздействию х (t) соответствует реакция а внешнему воздействию где А = const, реакция у(t) = Применение принципа наложения существенно облегчает исследование процессов в линейных электрических цепях, он лежит в основе многих широко используемых методов анализа.

Состояние теории цепей в значительной степени определяется степенью разработанности теории и методов решения соответствующих дифференциальных уравнений. К настоящему времени разработаны общие методы решения только линейных дифференциальных уравнений с постоянными коэффициентами, поэтому наиболее законченный вид имеет теория линейных инвариантных во времени цепей, которые в дальнейшем будем называть просто линейными цепями.

• Линейные цепи при гармоническом воздействии
• Нелинейные резистивные цепи
• Преобразование схем электрических цепей
• Установившиеся процессы в линейных электрических цепях
• Линии с распределенными параметрами
• Идеализированные пассивные элементы
• Идеализированные активные элементы
• Топологии электрических цепей

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Уравнение равновесия напряжений фазы обмотки якоря неявнополюсного СГ.

Уравнение равновесия напряжений фазы обмотки якоря явнополюсного СГ.

Уравнение равновесия напряжений СГ выглядит:

Здесь Е₀ – ЭДС в фазе статора наводимая потоком обмотки возбуждения

E_ad – ЭДС индуцируемая в обмотке якоря потоком продольной реакции якоря Ф_ad

E_aq — ЭДС индуцируемая в обмотке якоря потоком поперечной реакции якоря Ф_aq

E_as — ЭДС рассеяния индуцируемая в фазе обмотке якоря потоком рассеяния обмотки якоря Ф_as

r_a – активное сопротивление фазы обмотки якоря

Уравнение равновесия напряжений фазы обмотки якоря неявнополюсного СГ.

Уравнение равновесия напряжений СГ выглядит:

Здесь Е₀ – ЭДС в фазе статора наводимая потоком обмотки возбуждения

— индуктивное сопротивление рассеяния фазы обмотки статора

— индуктивное сопротивление продольной реакции якоря в следствии равномерности воздушного зазора

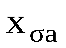
r_a – активное сопротивление фазы обмотки якоря

6. Векторные диаграммы синхронного генератора.

7. Характеристика холостого хода синхронного генератора.

8. Внешняя характеристика синхронного генератора.

9. Регулировочная характеристика синхронного генератора.

10. Характеристика 3-х фазного короткого замыкания синхронного генератора.

Характеристика трехфазного короткого замыкания представляет собой зависимость тока якоря при коротком замыкании от тока возбуждения I_K= f(I_B) при n=const (1!!)

11. Параллельная работа синхронных генераторов.

В том случае, когда мощность потребителя становится больше номинальной мощности работающего генератора, параллельно ему включают другой генератор.

Для включения синхронного генератора на параллельную работу с электрической сетью или другим, уже работающим синхронным генератором необходимо выполнить следующие условия:

напряжение подключаемой машины должно быть равно напряжению сети или работающей машины;

частота подключаемого генератора должна быть равна частоте сети;

напряжения всех фаз подключаемой машины должны быть противоположны (по фазе) напряжениям соответствующих фаз сети или работающей машины;

для подключения на параллельную работу трехфазного синхронного генератора необходимо также обеспечить одинаковое чередование фаз подключаемой машины и сети.

12. Угловая характеристика синхронного двигателя.

При холостом ходе двигателя оси ротора и статора совпадают,q= 0, соответственно M= 0,P= 0. С увеличением момента сопротивления нагрузки на валу ротор отстает от магнитного поля, а электрическая мощность P и электромагнитный момент M возрастают. Причем, в отличие от генераторного режима, M является полезным моментом, вращающим вал ротора, а активная мощность теперь потребляется двигателем от сети. При изменении угла q от 0 до +90°двигатель работает устойчиво. Если еще увеличить момент сопротивления нагрузки, то уголqпревысит значение +90°, а M,P начнут уменьшаться. При этом ротор начнет вращаться несинхронно с магнитным полем. Тогда двигатель перестанет работать параллельно с сетью —выпадет из синхронизма, что может вызвать нежелательные явления и рассматриваться как аварийный режим.

13. Механическая характеристика синхронного двигателя.

14. Способы синхронного генератора с сетью. Есть 2 способа.

1 При включении синхронного генератора на параллель­ную работу с сетью по способу точной синхронизации стре­мятся к тому, чтобы при включении не возникало больших бросков тока. Большие толчки тока вызывают большие мо­менты, действующие как на ротор, так и на статор, и силы, которые могут привести к разрушению обмотки статора.

2 При самосинхронизации неизбежно возникновение значительного толчка тока, так как включение невозбужденного генератора в сеть с напряжением U_С, эквивалентно внезапному короткому замыканию этого генератора при работе на холостом ходу с Е₀=U_С.Однако толчок тока при самосинхронизации будет все же меньше, так как, кроме сопротивления генератора, в цепи будут действовать также сопротивления элементов сети (повышающие трансформаторы, линия и т. д.).

15. U – образная характеристика синхронного генератора.

Предположим, что генератор после подключения на сеть работает без нагрузки и его ЭДС уравновешивает напряжение сети . Е этом увеличить ток в обмотке возбуждения, т. е. пере­возбудитьмашину, то ЭДС увеличится до значения и в цепи генератора появится избыточная ЭДС (рис. 21.10, а),вектор которой совпадает по направлению с вектором ЭДС . Ток , вызванный ЭДС , будет отставать от нее по фазе на 90° (поскольку ). По отношению к ЭДС этот ток также будет отстающим (индуктивным). С увеличением перевоз­буждения значение реактивного (индуктивного) тока увеличится.

Если же после того, как генератор подключен к сети, умень­шить ток возбуждения, т. е. недовозбудить машину, то ЭДС уменьшится до значения и в цепи генератора опять будет действовать избыточная ЭДС . Теперь вектор этой ЭДС будет совпадать по направлению с вектором напряжения сети (рис. 21.10, б), и поэтому ток , вызванный этой ЭДС и отстающим от нее по фазе на 90°, будет опере­жающим (емкостным) по отношению к ЭДС генератора .

Это сопровождается появлением в обмотке статора реактивного тока , которым по отношению к ЭДС является отстающим (индуктивным). Вы званная этим током продольно-размагничивающая реакция якоря компенсирует избыточную МДС возбуждения так, что ЭДС гене­ратора остается неизменной. Такой же процесс происходит и при недовозбуждении генератора с той лишь разницей, что в обмотке появляется опережающий (емкостный) ток , а вызванная этим током продольно-намагничивающая реакция якоря компен­сирует недостающую МДС возбуждения.

16. Пуск синхронных двигателей.

Одним из главных недостатков синхронных двигателей является сложность их пуска в ход. Пуск синхронных двигателей может быть осуществлен при помощи вспомогательного пускового двигателя. Пуск синхронного двигателя при помощи вспомогательного двигателя. Если ротор синхронного двигателя с возбужденными полюсами раскрутить другим, вспомогательным двигателем до скорости вращения поля статора, то магнитные полюсы статора, взаимодействуя с полюсами ротора, заставят ротор вращаться далее самостоятельно без посторонней помощи, в такт с полем статора, т. е. синхронно (откуда эти двигатели и получили свое название).

17. Сравнение синхронных и асинхронных двигателей.

Чтобы остановить выбор на синхронном или асинхронном двигателе для приведения во вращение того или иного производственного механизма, необходимо иметь в виду следующее.

Обмотки статора обоих двигателей получают питание от сети трехфазного переменного тока. Для питания обмотки возбуждения синхронного двигателя требуется, кроме того, источник электрической энергии постоянного тока, правда, относительно небольшой мощности.

Асинхронный пуск синхронных двигателей несколько сложнее пуска асинхронных двигателей с короткозамкнутым ротором. В отношении пусковых свойств асинхронные двигатели с фазным ротором имеют весьма существенные преимущества перед синхронными двигателями.

Частота вращения синхронных двигателей остается постоянной при изменении нагрузки, тогда как у асинхронных двигателей даже при их работе на естественной характеристике она несколько изменяется.

Асинхронные двигатели дают возможность регулировать частоту вращения различными способами,. Использование некоторых из этих способов для регулирования частоты вращения синхронных двигателей в принципе невозможно, а некоторых связано с большими конструктивными и эксплуатационными трудностями. Учитывая это, следует иметь в виду, что синхронные двигатели относятся к двигателям с нерегулируемой частотой вращения.

Воздействуя на ток возбуждения синхронного двигателя, можно в широких пределах изменять его коэффициент мощности. Можно, в частности, заставить синхронный двигатель работать с cos φ = 1, а также с опережающим током. Последнее может быть использовано для улучшения коэффициента мощности других потребителей, питающихся от той же сети. В отличие от этого асинхронный двигатель представлет собой активно-индуктивную нагрузку и имеет всегда cos φ

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

—> Сайт Георгия Таненгольца —> Главная | —> Мой профиль | —> Регистрация | —> Выход | —> Вход | RSS

Видео:Урок 251. Измерение напряжения и силы токаСкачать

—> —>Статистика —>

Видео:Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Баланс напряжений и Вольтамперная характеристика

Видео:Гальванические элементы. 1 часть. 10 класс.Скачать

Сначала прочитайте Что такое электричество и зачем оно нужно и Ток, напряжение, сопротивление. Закон Ома

Видео:Математика это не ИсламСкачать

10. Баланс напряжений.

Если мы получили некоторое количество электрической энергии за счет ЭДС. источника, то при протекании тока израсходуем всю эту энергию во всей цепи.

В простейшей цепи имеется два сопротивления — сопротивление приемника (нагрузки) и сопротивление самого источника. R нагрузки и r источника

ЭДС. источника создает ток в цепи, при этом на нагрузке, и на самом источнике, возникает напряжение. (правильно сказать — падение напряжения)

То есть, напряжение возникает на всех сопротивлениях, где протекает ток, поэтому напряжение возникает как на внешней нагрузке, так и на внутреннем сопротивлении источника.

Е – это ЭДС

E = U + U вн ЭДС равна сумме падений напряжения во внешней цепи на внутреннем сопротивлении источника.

То же самое E = IR + Ir вн

Сумма падений напряжений на нагрузке и внутри источника равна ЭДС. Эту фразу надо выучить.

Из уравнения очевидно, что

Напряжение всегда равно ЭДС минус падение напряжения внутри самого источника.

Напряжение всегда меньше ЭДС. на величину падения напряжения внутри самого источника.

Таким образом, напряжение — это часть Электродвижущей силы, которая действует на внешнюю цепь.

Электрическая энергия, которую создает источник, расходуется в нагрузке и , к сожалению, в самом источнике.

Последнее обстоятельство очень важно понимать.

Ток, созданный источником, проходит по замкнутой цепи, то есть, через нагрузку и через сам источник.

Источник, обладает сопротивлением, оно — то и нагревается, значит, источник, часть созданной электрической энергии тратит на нагрев самого себя.

Следовательно, электрическая энергия, которую можно получить в источнике, не может быть вся израсходована полезно в нагрузке, часть энергии теряется бесполезно в самом источнике. Бесполезно потому, что нагрев самого источника абсолютно не нужен и, в большинстве случаев, вреден.

Видео:Урок 25. Что такое Переменный ТОК | Практические примерыСкачать

11. Виды простых электрических цепей.

Простые электрические цепи с несколькими сопротивлениями.

• Цепь с последовательными сопротивлениями.
• Цепь с параллельными сопротивлениями.
• Цепь со смешанным соединением сопротивлений.

Последовательное соединение сопротивлений

При последовательном соединении сопротивлений, между сопротивлениями нет узлов, и ток никуда не ответвляется, поэтому ток через последовательно соединенные сопротивления протекает один и тот же.

Полное (эквивалентное) сопротивление цепи равно сумме сопротивлений.

Сумма напряжений на сопротивлениях равна общему напряжению.Напряжение на каждом сопротивлении пропорционально сопротивлению.

Чем больше сопротивление, тем больше на нем напряжение

При последовательном сопротивлении нельзя отключать одно сопротивление, происходит разрыв цепи и все отключится.

Параллельное соединение сопротивлений

Узел — это точка, в которой сходится не менее трех проводов.
При параллельном соединении, сопротивления подключаются под общее напряжение, так, что в каждое сопротивление ответвляется свой ток. Точки подключения сопротивления являются узлами.

1 закон Кирхгоффа .

Сумма токов втекающих в узел равна сумме токов вытекающих из узла.

Алгебраическая сумма токов узла равна 0.

Смысл этого закона очень легко понять, если представить себе провода как трубы, а ток как воду.

Значит, ток разветвляется по этим сопротивлениям и в каждом сопротивлении протекает свой ток.

Сумма токов во всех сопротивлениях равна общему току.

I общ = I 1+ I 2+ I 3

Полное (эквивалентное) сопротивление всей цепи рассчитывается по формуле.

Обратная величина полного сопротивления всей цепи равна сумме обратных величин всех сопротивлений.

g — проводимость

Полная эквивалентная проводимость равна сумме

проводимостей всех ветвей.

Полное сопротивление всей цепи меньше наименьшего из всех параллельно соединенных сопротивлений.

Чем больше сопротивлений соединяется параллельно, тем меньше полное сопротивление цепи, и больше ток, который отдает источник. Это вполне логично, ведь чем больше подключается сопротивлений параллельно, тем больше путей для тока и ему легче идти.

Все сопротивления находятся под одним напряжением .

При параллельном соединении каждое сопротивление можно отключать и подключать, независимо от других.

В реальной практике, в силовых и осветительных сетях, к одному источнику подключается несколько нагрузок, при этом всегда нагрузки подключаются параллельно.

Это удобно, потому что они работают независимо друг от друга и рассчитаны на одно и то же напряжение, и значит, их легко стандартизовать.

Вспомните, сколько лампочек в вашей квартире, и все они подключены к одной паре проводов входящих в квартиру. Все лампочки рассчитаны на напряжение 220 В, и их можно включать и выключать независимо друг от друга.

Например, в автомобиле все потребители: лампочки, моторы и т.п. включены параллельно под напряжение 12 В.

Смешанное соединение это параллельное соединение, только некоторые ветви содержат по несколько последовательно соединенных сопротивлений.

Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

12. Электрическая мощность.

До сих пор с энергией было связано понятие напряжение и ЭДС.

Но все время оговаривалось, что напряжение — это удельная энергия, то есть энергия, которую затрачивает электрическое поле на перенос единичного электрического заряда.

Ток — это количество электрических зарядов протекающих через сечение проводника в единицу времени. Раз в единицу времени, значит, ток это скорость потока всех электрических зарядов участвующих в данном токе.

Теперь если мы возьмем и умножим скорость потока всех электрических зарядов на энергию единичного заряда (напряжение), то получим скорость совершения работы по перемещению всех электрических зарядов.

Скорость совершения работы — это мощность.

Электрическая мощность — это скорость, с которой электрическая энергия превращается в тепло на данном сопротивлении.

Электрическая мощность сопротивления равна произведению тока на напряжение.

Очень важно, что мощность пропорциональна квадрату тока.

Это значит, что если сопротивление меньше, то мощность все равно будет больше, это станет очевидно при решении задач.

P = E I Мощность, которую создает источник, равна произведению ЭДС источника на ток в цепи.

Мощность, которую создает источник и полезная мощность, которая получается на нагрузке, сильно отличаются. Вся мощность выделенная источником не может выделиться на нагрузке. КПД не может быть 100%. Часть мощности источника греет сам источник и, значит, что это мощность потерянная.

P = ( U – Ir вн ) I = U I – I 2 r вн

I 2 r вн – потери мощности в источнике

Мощность обозначается P

Мощность измеряется в Ваттах Вт

Мощность — наиболее важная результирующая характеристика приемника электрической энергии.

Например, лампочка мощность 100 Вт. дает больше света, чем лампочка мощность 75 Вт.

Электрическая энергия определяется как мощность, умноженная на время.

Электрическая энергия стоит денег, и мы за нее платим.

Лампочка мощность 100 Вт за 1 час превращает в тепло и свет электроэнергию 100 Вт*час. на сумму 12,8 коп.

Лампочка мощностью 75 Вт. за час превращает в тепло и свет электроэнергию 75 вт*час на сумму 9,6 коп.

Видео:Урок 14. Законы Кирхгофа простыми словами с примерамиСкачать

13. Закон Ома для всей цепи.

Зависимости всех параметров цепи устанавливает закон Ома для всей цепи.

Формула этого закона выводится из баланса напряжений.

( R нагрузки + r внутренее ) –это полное сопротивление цепи

Формула закона Ома для всей цепи

Ток в цепи прямо пропорционален ЭДС источника и обратно пропорционален полному сопротивлению цепи.

Смысл закона Ома для всей цепи понятен, если понятен баланс напряжений в цепи.

ЭДС — постоянное свойство источника. Она есть или ее нет. Например, если батарейка заряжена, то ее ЭДС равна 1,5 Вольта (это природа веществ, из которых состоит батарейка). ЭДС. автомобильного аккумулятора 12, 6 Вольта. Напряжение, которое получится на нагрузке, при подключении к этим источникам, может оказаться самым разным, но не больше ЭДС

Видео:Электрохимический ряд потенциалов. 1 часть. 10 класс.Скачать

14. Вольтамперная характеристика электрической цепи.

Сколько лампочек можно подключить к одной батарейке?

График зависимости напряжения от величины тока, который отдает источник. называется вольтамперная характеристика источника.

1. Почему может изменяться ток, который отдает источник?

2. Почему нагрузка может потреблять разный ток?

В сущности, это один и тот же вопрос.

Нагрузка — это приемники электрической энергии.

Если нагрузка — это обычная лампочка, то она, конечно, может потреблять ток только одной величины, потому что у нее (в нагретом состоянии) постоянное сопротивление, и тогда сама проблема теряет интерес. Но если мы подключим к источнику несколько лампочек, то каждая лампочка начнет потреблять свой ток. Две лампочку начнут потреблять больше ток, чем одна, три еще больше и т. д.

Итак, чем больше параллельно подключается лампочек к источнику, тем меньше суммарное сопротивление нагрузки, тем больший ток вынужден отдавать источник.

Как будут вести себя приемники электрической энергии и источник электрической энергии, если мы будем увеличивать количество параллельно подключаемых приемников?

То есть, как будет меняться напряжение, если увеличивается ток, который отдает источник?

При увеличении тока, напряжение снижается, почему?

График зависимости напряжения от величины тока, который отдает источник. называется вольтамперная характеристика источника.

Увеличиваем нагрузку, поочередно добавляем лампочки. Общий ток растет

По мере увеличения тока нагрузки напряжение на нагрузке падает .

Ток

Если не включать ни одной лампочки, то напряжение остается равным ЭДС

Такое состояние называется «Холостой ход»

Включаем одну лампочку, появляется ток 1. Напряжение снижается (вертикальный зеленый отрезок) и появляется падение напряжения внутри источника (Вертикальный оранжевый отрезок)

Лампочка горит нормально.

Включаем вторую лампочку, Токи лампочек складываются и общий ток увеличивается. От этого внутри источника увеличивается падение напряжения Ir .

Оранжевая линия длиннее, зеленая короче. Видно, что напряжение на двух лампочках стало ниже, чем было на одной горящей лампочке. Обе лампочки горят, но не так ярко, как горела одна.

Если включать следующие лапочки, то ток будет нарастать, падение напряжения внутри источника становится больше и напряжение на лампочках становится ниже, они горят тусклее. Сам источник начинает греться, так как большой ток на его внутреннем сопротивлении выделяет много тепла.

Последняя лампочка, которую ради интереса можно включить, приводит к тому, что напряжение на лампочках становится равным нулю. То есть вся ЭДС источника тратится на поддержание напряжение внутри источника. То есть падение напряжения внутри источника становится равным ЭДС Если еще включать лампочки, ничего не изменится, ток достиг максимальной величины, а напряжение остается равным нулю. Источник бесполезно греется. Такое состояние называют –«Короткое замыкание».

Как сделать так, чтобы все 5 лампочек, хоть как-то горели? Для этого надо взять другой – более мощный источник. У него должно быть меньше внутреннее сопротивление r вн. Тогда при включении лампочек, падение напряжения внутри источника Ir вн. станет меньше, а значит, напряжение на нагрузке станет больше.

График вольтамперной характеристики более мощного источника показан синей линией. Чтобы сделать такой источник, надо увеличить его размеры или, например, взять вместо тонкой батарейки, более толстую.

Когда ток достигает максимального значения, и напряжение падает до нуля, то это режим короткого замыкания

Такой характер зависимости справедлив для любых источников электрической энергии.

Видео:Уравнения напряжений обобщенного преобразователяСкачать

15. Режимы работы источника электрической энергии.

Рассматривают три режима работы электрической цепи

Холостой ход, короткое замыкание и номинальный режим.

Любая цепь может оказаться в любом из указанных режимов.

Это зависит от того какую нагрузку подключают к данному источнику, иначе говоря, это зависит от того какое соотношение получится между сопротивлением (нагрузки) внешней цепи и внутренним сопротивлением источника.

Холостой ход. — Все нагрузки отключены. Сопротивление нагрузки бесконечно больше внутреннего сопротивления источника.

В этом случае напряжение на выводах источника рано ЭДС источника.

О напряжении на нагрузке нет речи — нагрузка отключена.

Ток в цепи равен 0. Цепь разомкнута.

Источник работает, но для него это холостой ход

На холостом ходу ток равен 0.

Напряжение равно ЭДС

Мощность, которую отдает источник, равна 0.

На поддержание рабочего режима холостого хода, к сожалению, надо тратить некоторую небольшую внешнюю энергию, то есть на электростанции, например, надо сжигать небольшое количество угля, чтобы генератор крутился.

Номинальный режим.

Рассмотрим режим работы цепи, когда подключили малую нагрузку (одна лампочка).

— сопротивление нагрузки сравнимо с внутренним сопротивлением источника

— напряжение на нагрузке меньше величины ЭДС.на величину падения напряжения внутри источника

— напряжение еще довольно близко по величине к величине ЭДС

— мощность, которую создает источник, практически вся используется в нагрузке

— К.П.Д. довольно высок.

Этот режим можно назвать номинальным рабочим режимом с высоким К.П.Д.

Это режим, которому обычно соответствуют паспортные (данные) параметры источника: рабочее напряжение на нагрузке, ток, мощность.

В силовых и осветительных сетях короткое замыкание — это аварийный режим, и его допускать нельзя.

• включена очень большая нагрузка (например много лампочек одновременно), сопротивление нагрузки упало до нуля. То есть, сопротивление нагрузки бесконечно меньше сопротивления источника.

— напряжение на нагрузке упало до 0

— все напряжение создается только внутри источника

— мощность, которая выделяется на нагрузке, равна 0

— источник создает огромную электрическую мощность, но она вся тратится внутри самого источника на его нагрев, и источник может сгореть.

Холостой ход бесполезен, так как, при холостом ходе не работают никакие полезные нагрузки. В силовых и осветительных цепях холостой ход следует рассматривать как режим ожидания. В электронных схемах холостой ход применяют часто для поддержания максимального уровня напряжения сигнала.

Короткое замыкание бесполезно, так как нагрузки, хотя и подключены, они тоже не работают, потому что напряжение на них равно 0 и никакой полезной мощности выделить нельзя. Лапочки просто не горят. В электронных схемах режим короткого замыкания применяется для маломощных источников для поддержания стабильного тока сигнала.

Короткое замыкание — это такой режим, когда источник просто не может обеспечить работу нагрузки, говорят, что источник не тянет, не хватает мощности источника.

То есть, цепь должна работать в режиме когда нагрузка подключена но не слишком большая для данного источника. Такой режим называется – номинальный или рабочий . Все нагрузки работают под расчетным напряжением и источник не перегревается.

📹 Видео

Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Урок 143 (осн). Электрический ток. Источники токаСкачать

Урок 147 (осн). Сила тока. Единицы силы тока. АмперметрыСкачать

Урок 250. Задачи на расчет электрических цепей - 1Скачать

Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Резонанс в колебательном контуреСкачать

Урок 359. Конденсатор и катушка индуктивности в цепи переменного тока.Скачать