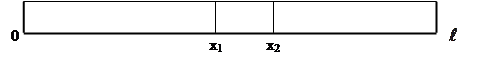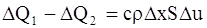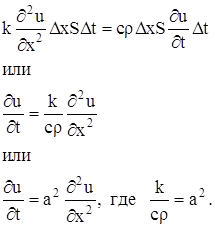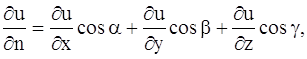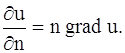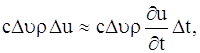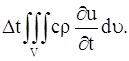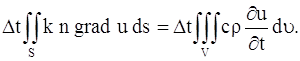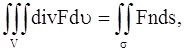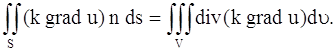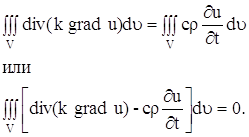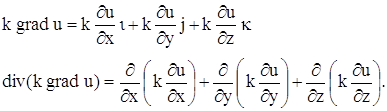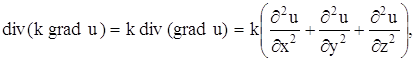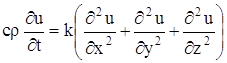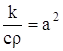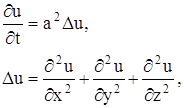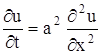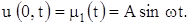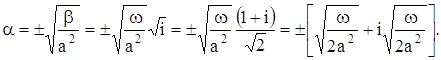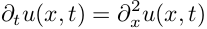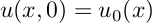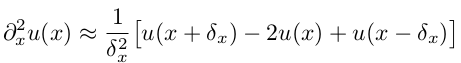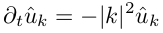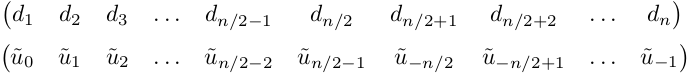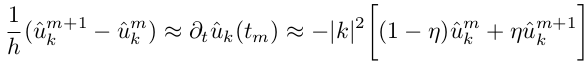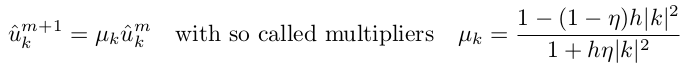Уравнения распространения тепла в неограниченном стержне (2 видео)

Уравнение распространения тепла в стержне

2.1.1. Уравнение распространения тепла в стержне.

Рассмотрим однородный стержень длины 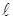. Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.

Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = 0, а другой – с точкой х = .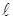

Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой

(1)

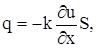
где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.

Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х₁ и х₂ (х₂ – х₁ = х). Количество тепла, прошедшего через сечение с абсциссой х₁ за время t, будет равно

(2)

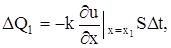
то же самое с абсциссой х₂:

(3)

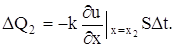
Приток Q₁ — Q₂ в элемент стержня за время t будет равняться:

(4)

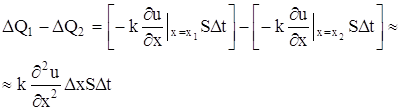
Этот приток тепла за время t затратился на повышение температуры элемента стержня на величину u:

(5)

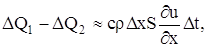
где с – теплоемкость вещества стержня, 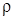– плотность вещества стержня (xS – масса элемента стержня).

Приравнивая выражения (4) и (5) одного и того же количества тепла 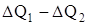, получим:

Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.

Чтобы решение уравнения (6) было вполне определено, функция u (x, t) должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (6) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для 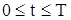, следующие:

u (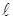, t) = ψ₂(t). (9)

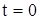
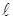
Физическое условие (7) (начальное условие) соответствует тому, что при в разных сечениях стержня задана температура, равная φ(x). Условия (8) и (9) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х = поддерживается температура, равная ψ₁(t) и ψ₂(t) соответственно.

Доказывается, что уравнение (6) имеет единственное решение в области 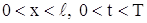, удовлетворяющее условиям (7) – (9).

2.1.2. Распространение тепла в пространстве.

Рассмотрим процесс распространения тепла в трехмерном пространстве. Пусть u (x, y, z, t) – температура в точке с координатами (x, y, z) с момент времени t. Опытным путем установлено, что скорость прохождения тепла через площадку s, т. е. количество тепла, протекающего за единицу времени, определяется формулой (аналогично формуле (1))

(10)

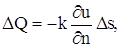
где k – коэффициент теплопроводности рассматриваемой среды, которую мы считаем однородной и изотропной, n – единичный вектор, направленный по нормали к площадке s в направлении движения тепла. Таким образом, можем записать:

где – направляющие косинусы вектора n, или

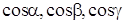
Подставляя выражение 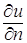в формулу (10), получаем:

Q = -k n grad u s.

Количество тепла, протекающего за время ∆t через площадку ∆s, будет равно:

Qt = -k n grad u t s.

Вернемся к поставленной задаче. В рассматриваемой среде выделим малый объем V, ограниченный поверхностью S. Количество тепла, протекающего через поверхность S, будет равно:

(11)

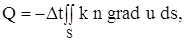
где n – единичный вектор, направленный по внешней нормали к поверхности S. Очевидно, что формула (11) дает количество тепла, поступающего в объем V (или уходящего из объема V) за время t. Количество тепла, поступившего в объем V, идет на повышение температуры вещества этого объема.

Рассмотрим элементарный объем υ. Пусть за время t его температура поднялась на u. Очевидно, что количество тепла, затраченное на это повышение температуры элемента υ, будет равно

где с – теплоемкость вещества, ρ – плотность. Общее количество тепла, затраченное на повышение температуры в объеме V за время t, будет

Но это есть тепло, поступающее в объем V за время t; оно определено формулой (11) . Таким образом, имеет место равенство

Сокращая на t, получаем:

(12)

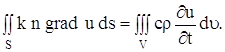
Поверхностный интеграл, стоящий в левой части этого равенства, преобразуем по формуле Остроградского (в векторной форме, где F – дивергенция векторного поля, 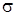– замкнутая поверхность)

полагая F = k grad u:

Заменяя двойной интеграл, стоящий в левой части равенства (12), тройным интегралом, получим:

Применив теорему о среднем к тройному интегралу, стоящего слева, получим :

(14)

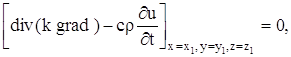
где P (x, y, z) – некоторая точка объема V.

Так как мы можем выделить произвольный объем V в трехмерном пространстве, где происходит распространение тепла, и так как мы предполагаем, что подынтегральная функция в равенстве (13) непрерывна, то равенство (14) будет выполняться в каждой точке пространства. Итак,

(15)

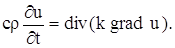
Подставляя в уравнение (15), получаем:

(16)

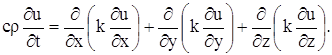
Если k – постоянное, то

и уравнение (15) в этом случае дает:

или, положив

(17)

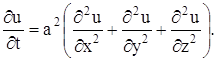
Коротко уравнение (17) записывается так:

где u – оператор Лапласа. Уравнение (17) и есть уравнение теплопроводности в пространстве. Для того чтобы найти единственное решение, отвечающее поставленной задаче, нужно задать краевые условия.

Пусть имеем тело 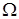, поверхность которого . В этом теле рассматривается процесс распространения тепла. В начальный момент температура тела задана. Это соответствует тому, что известно значение решения при t = 0 – начальное условие:

u (x, y, z, 0) = φ (x, y, z). (18)

Кроме того, должна быть известна температура в любой точке М поверхности тела в любой момент времени t – граничное условие:

u (М, t) = ψ (М, t). (19)

(Возможны и другие граничные условия.)

Если искомая функция u (x, y, z, t) не зависит от z, что соответствует тому, что температура не зависит от z, то получаем уравнение:

(20)

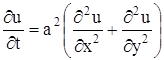
— уравнение распространения тепла на плоскости. Если рассматривается распространения тепла в плоской области D с границей С, то граничные условия, аналогично (18) и (19), формулируются так:

где φ и ψ – заданные функции, М – точка границы С.

Если же функция u не зависит ни от z, ни от y, то получаем уравнение

— уравнение распространения тепла в стержне.

§2.2. Температурные волны.

Задача о распространении температурных волн в почве является одним из первых примеров приложения математической теории теплопроводности, развитой Фурье, к изучению явлений природы.

Температура на поверхности земли носит, как известно, ярко выраженную суточную и годовую периодичность. Обратимся к задаче о распространении периодических температурных колебаний в почве, которую будем рассматривать как однородное полупространство 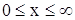. Эта задача является характерной задачей без начальных условий, так как при многократном повторении температурного хода на поверхности влияние начальной температуры будет меньше влияния других факторов, которыми мы пренебрегаем (например, неоднородность почвы). Таким образом, приходим к следующей задаче:

найти ограниченное решение уравнения теплопроводности

(1)

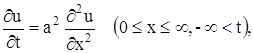
u (0, t) = A cos 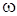t. (2)

Предполагается, что функции u (x, t) и m (t) ограничены всюду, т.е.

Запишем граничное условие в виде

(2’)

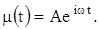
Из линейности уравнения теплопроводности следует, что действительная и мнимая части некоторого комплексного решения уравнения теплопроводности каждая в отдельности удовлетворяет тому же решению.

Если найдено решение уравнения теплопроводности, удовлетворяющее условию (2’), то его действительная часть удовлетворяет условию (2), а мнимая – условию

Итак, рассмотрим задачу:

(3)

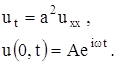
Ее решение будем искать в виде

(4)

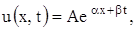
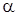
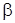
где и — неопределенные пока постоянные.

Подставляя выражение (4) в уравнение (3) и граничное условие, находим:

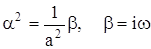
Для u (x, t) имеем:

(5)

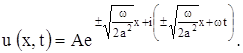
Действительная часть этого решения

(6)

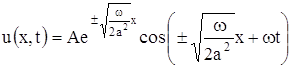
удовлетворяет уравнению теплопроводности и граничному условию (2). Формула (6) в зависимости от выбора знака определяет не одну, а две функции. Однако только функция, соответствующая знаку минус, удовлетворяет требованию ограниченности. Таким образом, решение поставленной задачи получаем в виде

(7)

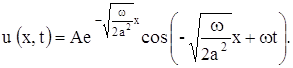
На основании полученного решения можно дать следующую характеристику процесса распространения температурной волны в почве. Если температура поверхности длительное время периодически меняется, то в почве также устанавливаются колебания температуры с тем же периодом, причем:

1.Амплитуда колебаний экспоненционально убывает с глубиной

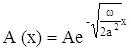
т.е. если глубины растут в арифметической прогрессии, то амплитуды убывают в геометрической прогрессии (первый закон Фурье).

2. Температурные колебания в почве происходят со сдвигом фазы. Время 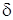запаздывания максимумов (минимумов) температуры в почве от соответствующих моментов на поверхности пропорционально глубине

Содержание

Лекция 4. Вывод уравнения теплопроводности
Начальные условия и граничные условия.
Решение первой начально-краевой задачи для уравнения теплопроводности.
Спектральный метод на примере простых задач матфизики
Одномерная задача распространения тепла по стержню
Двумерное уравнение диффузии
Двумерное волновое уравнение
Выводы
🔍 Видео

Видео:Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Лекция 4. Вывод уравнения теплопроводности

При построении математической модели распространения тепла в стержне сделаем следующие предположения:
1) стержень сделан из однородного проводящего материала с плотностью ρ;
2) боковая поверхность стержня теплоизолирована, то есть тепло может распространяться только вдоль оси ОХ;
3) стержень тонкий — это значит, что температура во всех точках любого поперечного сечения стержня одна и та же.

Рассмотрим часть стержня на отрезке [х, х + ∆х] (см. рис. 6) и воспользуемся законом сохранения количества тепла:

Общее количество тепла на отрезке [х, х + ∆х] = полному количеству тепла, прошедшему через границы + полное количество тепла, образованного внутренними источниками.

Общее количество тепла, которое необходимо сообщить участку стержня, чтобы повысить его температуру на ∆U, вычисляется по формуле: ∆Q= CρS∆x∆U, где С — удельная теплоемкость материала ( = количеству тепла, которое нужно сообщить 1 кг вещества, чтобы поднять его температуру на 1°), S — площадь поперечного сечения.

Количество тепла, прошедшее через левый конец участка стержня за время ∆t (тепловой поток) вычисляется по формуле: Q₁ = -kSU_x(x, t)∆t, где k — коэффициент теплопроводности материала ( = количеству тепла, протекающего в секунду через стержень единичной длины и единичной площади поперечного сечения при разности температур на противоположных концах, равной 1°). В этой формуле особого пояснения требует знак минус. Дело в том, что поток считается положительным, если он направлен в сторону увеличения х, а это, в свою очередь, означает, что слева от точки х температура больше, чем справа, то есть U_x CpS∆x∆U = kSU_x(x + ∆х, t) ∆t — kSU_x(x, t)∆t.

Если это равенство поделить на S∆x∆t и устремить ∆х и ∆t к нулю, то будем иметь:

Отсюда уравнение теплопроводности имеет вид

U_t = a 2 U_xx,
где 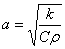— коэффициент температуропроводности.

В случае, когда внутри стержня имеются источники тепла, непрерывно распределенные с плотностью q(x,t), получится неоднородное уравнение теплопроводности

Начальные условия и граничные условия.

Для уравнения теплопроводности задается только одно начальное условие U|_t=0 = φ(х) (или в другой записи U(x,0) = φ(х)) и физически оно означает, что начальное распределение температуры стержня имеет вид φ(х). Для уравнений теплопроводности на плоскости или в пространстве начальное условие имеет такой же вид, только функция φ будет зависеть, соответственно, от двух или трех переменных.

Граничные условия в случае уравнения теплопроводности имеют такой же вид, как и для волнового уравнения, но физический смысл их уже иной. Условия первого рода (5) означают, что на концах стержня задана температура. Если она не изменяется со временем, то g₁(t) ≡ Т₁ и g₂(t) ≡ Т₂, где Т₁ и Т₂ — постоянные. Если концы поддерживаются все время при нулевой температуре, то Т₁= Т₂ = 0 и условия будут однородными. Граничные условия второго рода (6) определяют тепловой поток на концах стержня. В частности, если g₁(t) = g₂(t) = 0, то условия становятся однородными. Физически они означают, что через концы не происходит теплообмен с внешней средой (эти условия еще называют условиями теплоизоляции концов). Наконец, граничные условия третьего рода (7) соответствуют случаю, когда через концы стержня происходит теплообмен с окружающей средой по закону Ньютона (напомним, что при выводе уравнения теплопроводности мы считали боковую поверхность теплоизолированной). Правда, в случае уравнения теплопроводности условия (7) записываются немного по-другому:

Физический закон теплообмена со средой (закон Ньютона) состоит в том, что поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды. Таким образом, для левого конца стержня он равен Здесь h₁ > 0 — коэффициент теплообмена с окружающей средой, g₁(t) — температура окружающей среды на левом конце. Знак минус поставлен в формуле по той же причине, что и при выводе уравнения теплопроводности. С другой стороны, в силу теплопроводности материала поток тепла через этот же конец равен Применив закон сохранения количества тепла, получим:

Аналогично получается условие (14) на правом конце стержня, только постоянная λ₂ может быть другой, так как, вообще говоря, среды, окружающие левый и правый конец, бывают разные.

Граничные условия (14) являются более общими по сравнению с условиями первого и второго рода. Если предположить, что через какой-либо конец не происходит теплообмена со средой (то есть коэффициент теплообмена равен нулю), то получится условие второго рода. В другом случае предположим, что коэффициент теплообмена, например h₁, очень большой.

Перепишем условие (14) при х = 0 в виде и устремим . В результате будем иметь условие первого рода:

Аналогично формулируются граничные условия и для большего числа переменных. Для задачи о распространении тепла в плоской пластине условие означает, что температура на ее краях поддерживается нулевой. Точно так же, условия и внешне очень похожи, но в первом случае оно означает, что рассматривается плоская пластина и края ее теплоизолированы, а во втором случае оно означает, что рассматривается задача о распространении тепла в теле и поверхность его теплоизолирована.

Решение первой начально-краевой задачи для уравнения теплопроводности.

Рассмотрим однородную первую начально-краевую задачу для уравнения теплопроводности:

Найти решение уравнения

удолетворяющее граничным условиям

и начальному условию

Решим эту задачу методом Фурье.

Шаг 1. Будем искать решения уравнения (15) в виде U(x,t) = X(x)T(t).

Найдем частные производные:

Подставим эти производные в уравнение и разделим переменные:

По основной лемме получим

Теперь можно решить каждое из этих обыкновенных дифференциальных уравнений. Обратим внимание на то, что используя граничные условия (16), можно искать не общее решение уравнения б), а частные решения, удолетворяющие соответствующим граничным условиям:

Шаг 2. Решим задачу Штурма-Лиувилля

Эта задача совпадает с задачей Штурма-Лиувилля, рассмотренной в лекции 3. Напомним, что собственные значения и собственные функции этой задачи существуют только при λ>0.

Собственные значения равны

Собственные функции равны (См. решение задачи)

Шаг 3. Подставим собственные значения в уравнение а) и решим его:

Шаг 4. Выпишем частные решения уравнения (15):

В силу линейности и однородности уравнения (15) их линейная комбинация

Шаг 5. Определим коэффициенты A_n в (19), используя начальное условие (17):

Приходим к тому, что начальная функция φ(x) разлагается в ряд Фурье по собственным функциям задачи Штурма-Лиувилля. По теореме Стеклова такое разложение возможно для функций, удовлетворяющих граничным условиям и имеющих непрерывные производные второго порядка. Коэффициенты Фурье находятся по формулам

Вычислив эти коэффициенты для конкретной начальной функции φ(x) и подставив их значения в формулу (19), мы тем самым получим решение задачи (15), (16), (17).

Замечание. Используя формулу (19), можно также, как в лекции 3, получить решение первой начально-краевой задачи для уравнения U_t = a 2 U_xx. Оно будет иметь вид

где

Видео:8.2 Теплопроводность на отрезке. Сложные задачи.Скачать

Спектральный метод на примере простых задач матфизики

В этой статье описан псевдоспектральный метод численного решения уравнений матфизики, используемый в вычислительной гидродинамике, геофизике, климатологии и во многих других областях.

Одномерная задача распространения тепла по стержню

Для начала рассмотрим простую одномерную задачу распространения тепла в стержне. Уравнение, описывающее распространение тепла при некотором начальном распределении температуры по стержню:

Такое уравнение решается аналитически методом разделения переменных, например здесь, но нас интересует как это можно сделать численно. Прежде всего нужно определиться, как считать вторую пространственную производную по х. Проще всего это делается каким-нибудь разностным методом, например:

Но мы поступим иначе. Распределение температуры есть функция координаты и времени, и в каждый момент времени эта функция может быть представлена в виде суммы ряда Фурье, который в численном виде обрезается на n-ом члене:

Где u^«с крышечкой» — это коэффициенты разложения ряда Фурье. Подставим выражение для ряда в уравнение переноса тепла:

Получаем уравнение для коэффициентов Фурье, в котором отсутствует производная по координате! Теперь это обыкновенное дифференциальное уравнение, а не в частных производных, которое можно решить простым разностным методом. Уже легче, теперь остается найти коэффициенты разложения и в этом нам очень поможет быстрое преобразование Фурье (дальше FFT).

Логика здесь следующая:

1) в начальный момент времени дана функция координаты, описывающая распределение температуры по стержню;
2) разбиваем стержень на сетку из n точек;
3) находим комплексные коэффициенты Фурье с помощью алгоритма FFT, обозначим операцию как F(u);
4) умножаем полученные коэффиценты на -|k| 2 , получаем Фурье-образ второй производной. Аналогично можно получить Фурье-образ производной более высоких порядков p, достаточно умножить на (ik) p ;
5) делаем обратное преобразование Фурье F -1 (u), с помощью алгоритма IFFT, получаем значения второй производной в точках на сетке;
6) делаем шаг по времени, уже обычной разностной, явной или неявной, схемой;
7) повторяем.

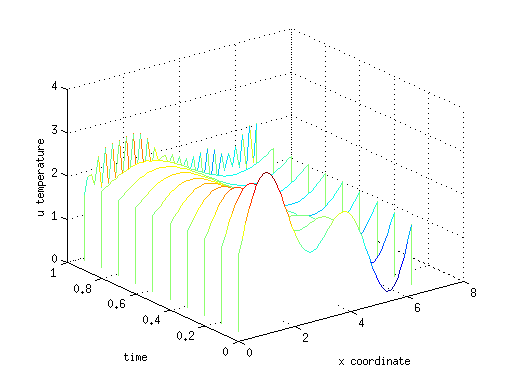
Рассмотрим теперь как это работает в программе для Matlab/Octave. В качестве начального распределения температуры возьмем гладкую функцию u0=2+sin(x)+sin(2x), стержень длинной 2π разобьем на 50 точек, с шагом по времени h=0.1, граничные условия периодичные (кольцо).

Стоит отметить особенность алгоритма FFT в Matlab, связанную с тем, что полученные коэффициенты разложения на выходе d=fft(u) идут не по порядку, а смещены, первая половина на месте второй и наоборот. Cначала идут коэффициенты с номерами от 0 до n/2-1, потом с номерами от -n/2 до -1. С этим были проблемы…

Полученное решение можно видеть на графике в виде «водопада» линий распределения температуры по х для каждого момента времени t. Видно, что решение испытывает ~~сильные осциляции~~ численную неустойчивость, связано это с невыполнением критерия Куранта. Избавиться от неустойчивости можно уменьшив шаг по времени, либо применяя более продвинутую неявную схему, например Кранка-Николсона.

Двумерное уравнение диффузии

Начальные условия: u0 = 1 + sin(2X) + cos(2Y), где u теперь 2d-массив u(i,j). Используем неявную схему интегрирования по времени (т.е. выразим m+1 шаг через m-й):

Можно доказать, что такая неявная схема никогда не расходится при η>0.5, будем использовать η=1. Таким образом каждое новое значение u m+1 получаем умножением u m на коэффициент μ_k, зависящий от временного шага и волновых чисел k, т.е. μ_k — это константа, которую не нужно пересчитывать на каждом шаге!

Двумерное волновое уравнение

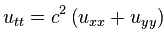
В волновом уравнении присутствует вторая производная по времени, поэтому задача сводится к системе двух обыкновенных диффуров, одна переменная — u, вторая — u_t, схему по времени в коде использовал самую простую явную, поэтому точность небольшая, шаг по времени очень маленький, зато код выглядит относительно просто. Впрочем, этого хватает для демонстрации работоспособности метода.

Периодичные граничные условия:

Фиксированные граничные условия (0 на краях, отражение волн от границ):

Выводы

В статье продемонстрировано несколько примеров применения спектрального метода для простых задач матфизики. Основная суть суть спектрального метода, это замена исходных диффренциальных уравнений в частных произодных на обыкновенные диффуры для коэффициентов разложения искомых функций по некоторому базису. Базисом могут быть синусы-косинусы, комплексные экспоненты, ортогональные полиномы, если требует геометрия — цилиндрические или сферические функции. Найденные коэффициенты в каждый момент времени позволяют восстановить искомое решение, а алгоритм FFT позволяет делать это быстро.

Преимуществами метода являются: